1 RangePair计数,Miner线性累积损伤假设,伪损伤
如图1(a)所示,无论是一个怎样的时域信号(不管它是左前轮六分力的垂向分量,还是轴头加速度,抑或是减振器的相对位移……),都可以通过Range Pair计数将较小的幅值循环从随机载荷中分离和计数出来,最终得到这样一个计数结果:幅值(Range)是多么大的载荷在刚才那样一个随机时域信号中出现了多少回(Pair)。
在此基础上,结合Miner线性累积损伤假设,可以将时域信号转化成与损伤相关联的一种数值。Miner线性累积损伤假设不难理解:如图1(b)所示,如果对于一个结构施加单一的恒幅值载荷
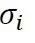
,根据相应的SN曲线可以知道该结构能够承受
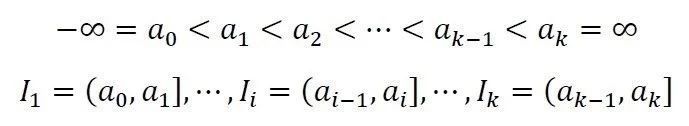
周次的循环载荷;但是,如果经由Range Pair计数发现某一随机载荷过程中对应于幅值为
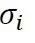
的载荷实际上一共出现了
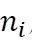
周次,那么,我们说幅值为
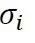
的载荷造成的损伤

为
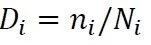
。而这一随机载荷造成的总损伤D即为这段随机载荷中大大小小不同幅值的载荷造成损伤的“线性累积”,也就是
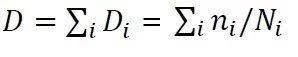
。
(a) Range Pair计数示意图
(b) Miner线性损伤累积假设示意图
图1 RangePair计数与Miner线性累积损伤假设1
这种将某一随机载荷向损伤进行的转化是非常粗糙的,因为这里面有太多在进行材料和结构疲劳寿命评估时需要考虑的因素都没有考虑在内,因此在车辆耐久性工程领域,我们习惯于把这种转化生成的与损伤相关联的量值称为“伪损伤”(Pseudo Damage),或者“相对损伤”。
这两个名字实在是取的比较妙。“伪损伤”,在于提示和强调,这种损伤数值是“伪”的,是假的,把这些个数值取倒数,并不对应疲劳寿命结果。那么这种量值的存在还有什么意义呢?“相对损伤”的命名提醒我们,要从“相对”的角度去理解和利用这一计算结果。如图2所示,如果让六个司机、驾驶同一车辆、在同一路面上各跑一圈,取得六个数据样本,那么对这六个时域数据样本都进行Range Pair计数,继而计算伪损伤,如图2所示,伪损伤的数值有一个分布和变化,有的大,有的小,这反映了驾驶习惯的变异性。如上所述,从每一个损伤的数值来看,这六个损伤数值都是“伪”的,但是,这六个数值之间的“相对”关系是真实的,也就是说谁开车开的比较“费”,谁开的比较“省”,这种相对关系的反应是客观的。究其原因,是在伪损伤的计算过程中,抓住了载荷幅值变化对于材料和结构疲劳寿命影响这个最主要的因素,因此尽管其结果比较粗糙,但是从相对意义上去理解和利用这一信息还是可以的。
千万不能瞧不起伪损伤这一粗糙的计算结果,我们将看到,伪损伤在车辆耐久性工程中是一个非常重要的量值,在整个车辆耐久性工程研发的各个环节,发挥着贯穿始终和穿针引线的作用。
图2 从相对损伤的角度理解和运用伪损伤1
由于车辆耐久性的设计指标往往关联于某一设计里程,因此常常将一段载荷的伪损伤数值D除以这段载荷所对应的行驶里程L,并将这一数值称为伪损伤密度d=D/L,在使用起来更加方便。与伪损伤相关的还有其他几个常用的“变体”,如等效载荷幅值,也都大同小异。
2 车辆耐久性工程中的重要随机变量
什么是随机变量?简单的说,随机变量就是“其值随机会而定”的变量。正确把握这一概念的关键在于事件发生的前后:在事件发生前,我们不知道它最终将取何值,这个要凭机会(随机的意思就在于此);而一旦事件发生,它取什么值就确定了。
车辆耐久性工程中的重要“事件”是什么呢?车辆累积行驶里程达到设计里程。比如,对于乘用车而言,这一事件为车的累积行驶里程达到(比如说)30万公里;对于商用车而言,这一事件为车的累积行驶里程达到(比如说)120万公里。
车辆耐久性工程中的重要随机变量是什么呢?有很多,比如说随机变量X1:
X1 = 车辆累积行驶里程达到设计里程时左前轮垂向六分力对应的伪损伤
类似的:
X2 = 车辆累积行驶里程达到设计里程时左前轮轴头垂向加速度对应的伪损伤密度
X3 = 车辆累积行驶里程达到设计里程时左前悬减振器相对位移对应的等效载荷幅值
概括起来,车辆耐久性工程中的重要随机变量是:
Xi = 车辆累积行驶里程达到设计里程时车辆某处的某载荷对应的伪损伤(或伪损伤密度,或等效载荷幅值,……)
在《车辆耐久性工程的核心挑战及应对》一文中我们谈到过,由于无法对于客户使用车辆的条件进行有效的限定,车辆达到设计里程时所经受的载荷是一个离散非常严重的随机变量。根据Fisher先生对于统计学任务的概括,本篇文章围绕着“定模型”展开一点探讨,也就是,“车辆累积行驶里程达到设计里程时,车辆某处的某载荷对应的伪损伤”Xi =x的概率p = f (x)服从怎样的分布?如何确定和证明它服从的是这样一种分布,而不是另外一种分布?这里面涉及的问题称为拟合优度检验,属于统计学中假设检验的范畴,将涉及到两位统计学大家K. Pearson和R. A. Fisher在上世纪初得到的重要成果。
3 他有没有出老千!
一个哥们儿在赌场玩筛盅,如鱼得水,被人怀疑在筛子上做了手脚,这种情况下如何分别是非?
我们需要为了这场官司做一些“统计试验”。随机的把这个筛子抛n次(也就是统计试验重复n次),比如说n=60次,记录下每一次获得的点数。“理论”上说,如果这个筛子做的不偏不倚,每一个点数出现的机会(概率pi)都是一样的,也就是pi=1/6,i=1,2,…,6,因此,理论上说每一个点数都会出现10次,当然,这是理想状态(理论值)。我把60次统计试验结果汇总,获得如表1所示,各个点数实际出现的次数vi,如表1所示,比如说v1=12,v2=13,等等。
表1 统计试验理论和实际试验结果汇总
显然,我们不指望每一个点数最终获得的试验结果也都是10次,与理论值百分之百的吻合,但是很自然的,如果表1中后两行差异越小,我们会越觉得实际结果与理论结果吻合的越好。现在要找出一个适当的量来反映这种差异。K. Pearson采用的量是
这个重要的统计量称为Pearson的拟合优度

统计量,简称

统计量。K. Pearson在1900年的证明:如果统计结果服从某一分布模型(本例中,如果筛子没有被做手脚而服从均匀分布模型),那么在样本大小
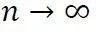
时(也就是将掷筛子的试验无穷尽的进行下去),Z的分布趋向于k-1自由度的

分布,即
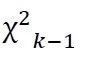
,本例中k=6。这样,我们可以根据K. Pearson的重要结论对于筛子是否被做过手脚这件事给出一个科学和明确的判断。
4

检验
我们将上一小节由K. Pearson提出的拟合优度检验方法称之为

检验。在上一小节中我们用一个掷筛子的例子,基本阐述了进行

检验的要点、步骤和流程。但是,掷筛子的例子是一个离散型的分布模型,而第2小节提到的车辆工程中的重要随机变量Xi是一个连续型的随机变量,其对应的分布模型也将是连续型的分布模型。在针对该连续型的随机变量进行

检验时,其大的流程框架不变,但是在一些细节的处理上稍有不同,而且在某些情况下

检验所仰仗的核心定理也需要有所修正,这里面蕴含着K. Pearson一直没有意识到的一个错误,而这一错误直到1924年才被R. A. Fisher纠正过来。
假设我们想证明或判断一下,某连续性随机变量是否服从正态分布,而该正态分布的两个参数,均值和方差,我们是事先不知道的,这个情形是我们在实际工程中最常见的状况。那么如何把这一情形转化成上一小节掷筛子的情形呢?
首先,把随机变量在其取值范围上分割成k个区间
为了获得表1中的理论解,我们需要计算正态分布模型在每个区间中的概率,这一过程并不好算,一个近似的方法是通过参数估计(这是下一篇文章谈论的话题)获得样本均值和样本方差,从而确定正态分布模型,然后计算该正态分布模型“落在”各个区间上的理论值。
试验值比较好算,根据实际试验结果看看落在各个区间上的试验值是多少就可以。这样,问题就回到了上一小节的情形。
我们注意到,刚才在确定正态分布的时候,分布模型的两个参数(均值和方差)我们事先是不知道的,需要通过参数估计获得这两个参数的估计值。这一细节使得K. Pearson在1900年给出的定理是有瑕疵的,R.A. Fisher在1924年纠正了这一缺陷,给出了如下完美的重要定理:
如果统计结果服从某一分布模型,而分布模型中有r个参数需要估计,那么在样本大小
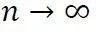
时,Z的分布趋向于k-1-r自由度的

分布,即
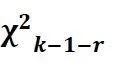
,定理中k表示划分成的区间数目。
运用

检验,我们可以对于车辆耐久性工程中的重要随机变量,即
Xi = 车辆累积行驶里程达到设计里程时车辆某处的某载荷对应的伪损伤(或伪损伤密度,或等效载荷幅值,……)
服从什么样的分布得出明确的结论,这一工作在车辆耐久性工程中已经有了相当的积累,目前一般认为2,Xi 服从对数正态分布。而其他行业对类似问题的研究也已经取得了一些重要的结论,如图3所示,可供参考。
有了

检验这一利器,即便面对一些不太熟悉的随机变量、对其服从什么分布的问题不是很清楚,只要有一些样本数据的支撑,就可以经由

检验给出明确的结论。
图3 航空航天行业典型使用工况中环境载荷所服从的分布3
附录:Karl Pearson(1857~1936),生卒于伦敦,公认为统计学之父。K. Pearson 最重要的学术成就,是为现代统计学打下基础。许多熟悉的统计名词如标准差,成分分析,卡方检验都是他提出的。
参考文献
1. 来源于西门子工业软件有限公司内部资料.
2. P.Johannesson, M. Speckert, Guide to load analysis for durability in vehicleengineering, 2014, Edition I, John Wiley & Sons, Ltd.
3.Christian Lalanne, Mechanical environment test specification developmentmethod, 1997, Edition III.
李旭东,2003年毕业于大连理工大学机械工程学院,获工学学士学位;2008年毕业于北京大学力学系固体力学专业,获理学博士学位。2008年至2014年,就职于中国航空综合技术研究所,历任工程师、高级工程师;2015年至今,就职于西门子工业软件(北京)有限公司,任职耐久性应用工程师。长期专注于(金属)材料和结构耐久性和损伤容限分析方法研究。
作者个人微信号:lixudong2008 (添加微信号请注明“姓名+工作单位”)
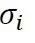 ,根据相应的SN曲线可以知道该结构能够承受
,根据相应的SN曲线可以知道该结构能够承受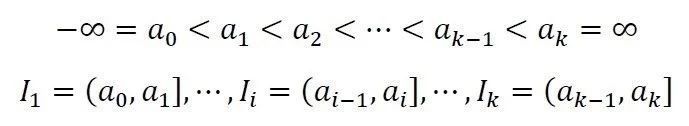 周次的循环载荷;但是,如果经由Range Pair计数发现某一随机载荷过程中对应于幅值为
周次的循环载荷;但是,如果经由Range Pair计数发现某一随机载荷过程中对应于幅值为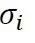 的载荷实际上一共出现了
的载荷实际上一共出现了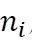 周次,那么,我们说幅值为
周次,那么,我们说幅值为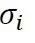 的载荷造成的损伤
的载荷造成的损伤 为
为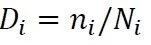 。而这一随机载荷造成的总损伤D即为这段随机载荷中大大小小不同幅值的载荷造成损伤的“线性累积”,也就是
。而这一随机载荷造成的总损伤D即为这段随机载荷中大大小小不同幅值的载荷造成损伤的“线性累积”,也就是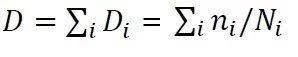 。
。



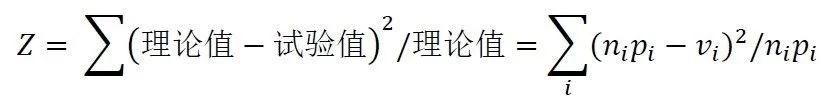
 统计量,简称
统计量,简称 统计量。K. Pearson在1900年的证明:如果统计结果服从某一分布模型(本例中,如果筛子没有被做手脚而服从均匀分布模型),那么在样本大小
统计量。K. Pearson在1900年的证明:如果统计结果服从某一分布模型(本例中,如果筛子没有被做手脚而服从均匀分布模型),那么在样本大小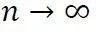 时(也就是将掷筛子的试验无穷尽的进行下去),Z的分布趋向于k-1自由度的
时(也就是将掷筛子的试验无穷尽的进行下去),Z的分布趋向于k-1自由度的 分布,即
分布,即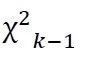 ,本例中k=6。这样,我们可以根据K. Pearson的重要结论对于筛子是否被做过手脚这件事给出一个科学和明确的判断。
,本例中k=6。这样,我们可以根据K. Pearson的重要结论对于筛子是否被做过手脚这件事给出一个科学和明确的判断。 检验
检验 检验。在上一小节中我们用一个掷筛子的例子,基本阐述了进行
检验。在上一小节中我们用一个掷筛子的例子,基本阐述了进行 检验的要点、步骤和流程。但是,掷筛子的例子是一个离散型的分布模型,而第2小节提到的车辆工程中的重要随机变量Xi是一个连续型的随机变量,其对应的分布模型也将是连续型的分布模型。在针对该连续型的随机变量进行
检验的要点、步骤和流程。但是,掷筛子的例子是一个离散型的分布模型,而第2小节提到的车辆工程中的重要随机变量Xi是一个连续型的随机变量,其对应的分布模型也将是连续型的分布模型。在针对该连续型的随机变量进行 检验时,其大的流程框架不变,但是在一些细节的处理上稍有不同,而且在某些情况下
检验时,其大的流程框架不变,但是在一些细节的处理上稍有不同,而且在某些情况下 检验所仰仗的核心定理也需要有所修正,这里面蕴含着K. Pearson一直没有意识到的一个错误,而这一错误直到1924年才被R. A. Fisher纠正过来。
检验所仰仗的核心定理也需要有所修正,这里面蕴含着K. Pearson一直没有意识到的一个错误,而这一错误直到1924年才被R. A. Fisher纠正过来。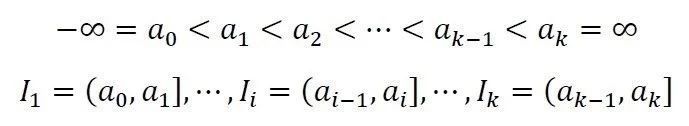
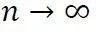 时,Z的分布趋向于k-1-r自由度的
时,Z的分布趋向于k-1-r自由度的 分布,即
分布,即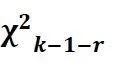 ,定理中k表示划分成的区间数目。
,定理中k表示划分成的区间数目。 检验,我们可以对于车辆耐久性工程中的重要随机变量,即
检验,我们可以对于车辆耐久性工程中的重要随机变量,即 检验这一利器,即便面对一些不太熟悉的随机变量、对其服从什么分布的问题不是很清楚,只要有一些样本数据的支撑,就可以经由
检验这一利器,即便面对一些不太熟悉的随机变量、对其服从什么分布的问题不是很清楚,只要有一些样本数据的支撑,就可以经由 检验给出明确的结论。
检验给出明确的结论。






 广告
广告





























































