广告
智能汽车运动预测和风险评估综述
2019-02-19 10:12:24· 来源：同济智能汽车研究所
本文由同济智能汽车研究所编译。《A survey on motion prediction and risk assessment for intelligent vehicles》原作者：Stephanie Lef`evre, Dizan Vasquez,
本文由同济智能汽车研究所编译。
《A survey on motion prediction and risk assessment for intelligent vehicles》
原作者：St´ephanie Lef`evre, Dizan Vasquez, Christian Laugier
编者按：安全性一直是智能汽车重点关注的话题。为了提升智能汽车安全性需要研究有效的风险评估方法，而相关方法的选取与车辆运动建模及运动预测有关。这篇综述介绍了三类车辆运动建模和两类风险评估方法，对智能汽车运动预测和风险评估的相关研究具有参考价值。
1、引言
根据建模的假设，运动建模和估计可以分为以下三个层次：
- 基于物理的运动模型——最简单的模型。它认为车辆的运动仅依赖于物理规律的约束。
- 基于行为的运动模型——更为高级的模型。它认为车辆未来的运动还依赖于驾驶员的意图。
- 感知/意识交互的运动模型——最为高级的模型，它认为驾驶员行为之间是相互依赖、相互影响的。
图1 运动模型概览
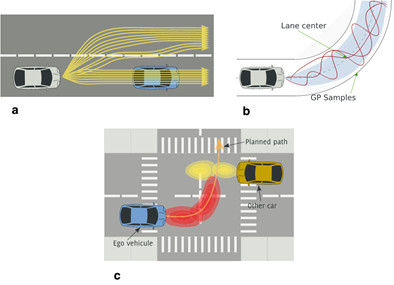
图2 运动预测范例
如图2所示，在运动模型的范例当中，基于物理的运动模型假设车辆是匀速和恒航向运动；基于行为的运动模型假设黑车是直行，蓝车是左转；感知/意识交互运动模型假设黑车直行，蓝车左转，在交叉路口，两车受交通规则约束。
风险的含义有两层：
- 实体之间的物理碰撞风险。
- 异于环境和场景期望的车辆行为（比如交通信号灯）。
2、基于物理的运动模型
根据相关的控制输入（转向、加速）、车辆特征（重量）和外部条件（路面摩擦系数），用动力学和运动学模型来预测未来的运动，以此来推算出车辆位姿/状态（位置、航向、速度）。
基于物理的运动模型在车辆的轨迹预测和碰撞风险评估方面已经有广泛的应用，目前也是最为通用的方法。这种运动模型的复杂程度取决于车辆运动学和动力学建模的精细程度、不确定性如何处理、是否考虑道路的几何特征等等。
2.1 车辆模型
a、动力学模型
基于拉格朗日方程，考虑了影响车辆运动的各种力，比如，轮胎的纵侧向力、道路航向[1]。
轮式车辆受诸如发动机、传动系、车轮等影响驾驶的复杂物理限制，同时考虑到车辆内在的参数，动力学模型会比较庞大。这种复杂性与控制应用相关，对于轨迹生成则可以采用简化的模型，二维平面的单车模型是使用比较广泛的[2-7]。
b、运动学模型
基于运动参数间的数学关系（例如位置、速度、加速度），并不考虑受力，并且假设在每个轮子的速度都在车轮的方向上[1]。在轨迹预测方面，运动学模型要比动力学模型更为流行，因为运动学模型更为简单。此外，由于动力学需要的车辆内部参数无法依靠外部的感知传感器获得，所以在智能交通系统当中涉及他车的运动，会排除使用动力学模型。
Schubert 等人对车辆运动学模型在轮式车辆的应用做了调研[8]。最简单的是假设车辆是直线运动的恒速（CV）和定加速度（CA）模型[9-13]。定转角速率与速度模型（CTRV）和定转角速率与模型（CTRA）通过引入横摆角和横摆角速率来考虑车辆绕Z轴的变化[10,12,14-17]。速度和横摆角速率的解耦使得模型的复杂程度依然较低。如果考虑用方向盘转角取代横摆角速率便得到了单车模型，也就考虑了速度和横摆角速率的相关性。对于这种方法，相应地可以推导出定方向盘转角与速度模型（CSAV）和定方向盘转角与加速度模型（CSAA）。
2.2 轨迹预测
a、单一轨迹模拟
最直接的方法是假设车辆当前状态完全已知以及车辆模型是完全可以描述车辆的运动，基于车辆当前状态，应用车辆模型去预测车辆未来的轨迹。
图3 定速轨迹预测模型
如图3所示，该策略可以使用动力学模型[2]或者运动学模型[11,13,17]。由于该模型的计算高效性，可以满足实时性要求。但是，该方法未考虑当前状态的不确定性和车辆模型的缺陷，预测的轨迹在长时间（不超过1s）下就会不可靠。
b、高斯噪声模拟
当前车辆状态和车辆模型的不确定性服从正态分布[9,10,12,16]。由于高斯噪声在卡尔曼滤波中的应用，它在描述不确定性方面很受欢迎。在递归的预测车辆状态时考虑传感器测量噪声，卡尔曼滤波是一个普适的方法。当车辆模型和传感器模型是线性的以及不确定性用正态分布描述时，就形成了一个贝叶斯滤波的特例。第一步（预测步），在时刻t估计的车辆状态推送给车辆模型，预测出时刻t+1以高斯分布的形式的车辆状态；第二步（更新步），在时刻t+1，传感器测得的状态结合预测状态得到时刻t+1，以高斯分布的车辆估计状态。每时每刻，对预测和更新循环，得到的车辆估计状态被称为滤波。
图4 定速运动模型和高斯噪声仿真的轨迹预测（椭圆代表的是预测位置的不确定性）
如图所示，通过预测步的循环，可以的得到未来每一时刻车辆状态的均值和协方差矩阵，转换后可以计算出联合了不确定性（每一时刻的正态分布）的均值轨迹[9,15,16]。
对比单一轨迹仿真模拟，高斯噪声模拟在预测轨迹不确定性方面有优势，但是，用一个单峰的正态分布对不确定性建模并不足以描述不同操作的可能性。一种解决方法是用混合高斯模型描述不确定性，典型的有切换卡尔曼滤波器（SKF）[18]。它使用一组描述车辆模型可能性的卡尔曼滤波器，并在各卡尔曼滤波器之间切换。SKF的一种替代策略是使用启发式方法根据环境的不同，切换不同的车辆运动学模型[12]。
c、蒙特卡洛模拟
一般来说（例如，当车辆模型不是线性的或者不确定性没有高斯特性），预测状态分布的解析表达式往往是未知的。蒙特卡洛方法提供了近似这种分布的手段。其思想在于对车辆模型的输入变量进行随机采样以生成潜在的未来轨迹。为了考虑路谱，可以在生成的轨迹当中加入权重，来惩罚那些不满足道路约束的轨迹，输入采样并不需要将输入视作固定值。典型的输入参数采样包括加速度、转向角或是侧向偏差。
考虑到动作的可执行性，那些大侧向加速度的轨迹样本可以剔除[21]；或者是考虑到车辆模型的物理限制，输入更多分布在可执行空间，这样，后处理过程中的移除不可执行轨迹也不是必要的[6,22]。示例如图5所示。不管当前状态是完全已知还是通过滤波的策略估计不确定的当前状态，蒙特卡洛模拟都可以用以预测车辆未来的状态。
图5 蒙特卡洛模拟的轨迹预测（黄色箭头）
2.3 方法的局限性
由于只考虑低层次的运动特性（动力学和运动学特性），基于物理的运动模型只能预测短期内（低于1s）的轨迹。它们不能预测执行一些特定操作（例如在一个十字路口，降速，定速转弯，然后加速过弯）时车辆运动的改变，或者是外部因素引起的车辆任何运动的变化（有前车引起的降速）。
3、基于行为的运动模型
把车辆看成是一个独立的行为实体，例如，它假设车辆在路网中的运动是执行一系列独立于其他车辆的行为产生的。行为定义为一个物理运动或是一系列需要技巧和注意力的动作[23]。这方面工作也有文献[24-28]开展。基于行为的运动模型的轨迹预测依赖于提前对驾驶员期望行为的识别。如果能够识别驾驶员的驾驶意图，那就可以假设预测的未来轨迹是与行为相匹配的。也正是这种提前的识别，使得该方法预测的轨迹从长远来看要比基于物理的运动模型更具有相关性和可靠性。基于行为的运动模型要么基于轨迹原型，要么基于驾驶意图估的行为。
3.1 轨迹原型
其思想是路网中的车辆轨迹可以归类为一簇有限的集群，每一种路径集对应一种典型的运动模式，如图6所示。通过对数据的训练和学习，可以得到轨迹原型中的运动模式，随后的预测便可以在在线给定部分轨迹时找到最近似的运动模式，并从轨迹原型中提取轨迹作为未来的运动预测。
图6 轨迹簇（每一种路径集对应一种典型的运动模式）
a. 表示法
使用学习样本轨迹（预先观测）得到的轨迹原型表示运动模式，是因为路网是结构化环境，一般假设可以提前识别运动模式（例如，从数字地图中提取，通过识别给定定位下所有可能操作/行为）。在这种条件下，不需要聚类过程，例如，训练集里面的每一条轨迹都已经分配到了一个集群当中。
自此，基于样本轨迹来取得运动模式有以下几种可能方法。一种方法是凝聚预先观测的轨迹，为每一种运动模式计算唯一的原型轨迹。例如，计算样本轨迹的均值和标准偏差可以推导出运动模式的随机表达式[30]。用以解释为什么执行一种运动模式会有变化的方法是为每一类运动模式建立多种原型轨迹，例如，训练样本的一个子集[31]。文献[32]提出了一种不一样的方法，不同的行为不是由单个的原型轨迹来表示，而是通过使用拓扑学习网络在线学习将原型轨迹合并成一个图形结构。
最近，一些文献表示，高斯过程（GPs）非常适合表示道路交通背景下的运动模式[25,33-35]。高斯过程可以看作是高斯概率分布的泛化。他们将一个过程建模为一个函数上的高斯分布。当应用到车辆轨迹时，假设学习数据集中的轨迹是样本函数，该函数来自于高斯过程。为此，学习包含在这些函数当中拟合一个高斯分布。高斯过程的主要优点是在观测轨迹时对噪声的鲁棒性（与前面所提的方法比较）和表达以一致和概率方式执行一个运动模式时变化的能力。例如，高斯过程表征的函数f(t)=(x,y)，（t是时间，（x,y）是二维平面的车辆坐标）可以部分考虑执行一个行为时的速度变化[25]。另一种方式是用函数对速度的位置建图以移除模型中的时间分量[33,34]。高斯过程的协方差用以捕捉交通条件变化引起的速度变化。但是，表征运动模式内部变化的能力用一个代价，高斯过程的简单实现的计算复杂度为O(n3)。
b. 轨迹预测
提取自车辆执行到目前的部分轨迹，轨迹预测可以通过对比提取轨迹和学习的运动模式，选择最有可能一条或一部分轨迹，将原型轨迹当作未来运动的模型。首先，需要定义标准衡量一个运动模型的部分轨迹距离。在高斯过程表征运动模式时，通过对未来可能轨迹的集成，这个距离用部分轨迹与高斯过程对应的概率计算[25,33,34]。在运动模式用有限原型轨迹表征时，这个距离通过测量部分轨迹与原型轨迹的相似程度得到。通过对比两条轨迹的相似程度，定义了若干标准，包括轨迹点的平均欧几里德距离[36]，豪斯多夫修正[29]，最长公共子串（LCS）[37]和基于四元旋转不变的LCS（平移旋转不变版本）[31]。
在计算出每一个运动模式的距离后，预测未来运动的最简单方法是选择最相似的运动模式并以一种独特的方式使用[36]。或者是看成多个模式的混合：计算不同运动模式的概率分布，然后要么将多个模式按权重结合为一个模式[33]，要么是以联合权重生成未来轨迹的集合[31,34]。最近发展起来的另一种方法是分层专家混合法[38]，它的优点是可以处理分类变量（例如，转向信号，道路布局的分类）。
c. 方法的局限性
长期以来，原型轨迹的主要限制是他们对时间定义的严苛。的确，当运动模式用有限的轨迹集表征时，必须使用庞大的原型轨迹来对执行一个运动模式的大量变化建模。例如，为了识别涉及在停止线等待一段时间的行为，不得不采取隐性阈值识别等待时间，并且忽略因此导致的两条轨迹的距离差。如何处理因交通负荷变化引起的速度微妙变化仍是这种模型待解决的问题。通过允许表征运动模式的时间独立，引入高斯过程在某种程度上解决了这个问题[33,34]。但是，高斯过程受到其他的限制。此外，考虑到计算的复杂程度，它们缺乏考虑车辆物理限制的能力，有可能会生成不现实的样本轨迹。我们目前所知的最好解决方法是Aoude等人在文献[34]中提出的方法，使用RRT对动态可行轨迹进行随机采样，采样得到的点作为车辆当前状态的输入，样本轨迹由高斯过程生成。
在使用原型轨迹的另一个难点是对不同道路布局的适应性，特别是在道路交叉口。由于每一个运动模型都是在一个特定交叉口几何拓扑下训练的，它们只能应用于类似交叉布局。
3.2 驾驶行为/意图估计和行为提取
有别于轨迹原型方法，首先估计驾驶员的行为意图（例如在停止线的等待，跟车，执行左转），然后预测与所识别的行为对应的可能操作的、连续的物理状态。相比轨迹原型，它的主要优势在于不用去匹配提前观测到的部分轨迹。而是采用提取更高层次的特征来识别行为，使得任意布局的学习模型实现起来更为容易。
用来提取驾驶员驾驶意图的线索有很多，例如：车辆状态、路网信息、驾驶员行为。在确定好行为之后，导入相应的控制量，结合动力学或者运动学模型便可以提取到预测轨迹。
a. 驾驶行为/意图估计
有许多线索可以用来估计驾驶员的驾驶行为/意图，例如，车辆物理状态（位置，速度，航向，加速度，横摆角速度，转向信号等等），路网信息（道路几何和拓扑，速度限制，交通规则等等），驾驶员行为（头部运动，驾驶风格等等）。大量驾驶行为/意图估计工作已经开展。这些工作集中在道路交叉口，但这里介绍的大部分方法可以应用到其他交通场景。
启发式方法等可以用来确定，在不久的未来，什么样的驾驶行为/意图会以一种确定的方式执行[39]。对于在更为复杂的场景中进行行为/意图分类，有识别力的学习算法十分流行，例如多层感知器（MLP）[28]，逻辑回归[40]，关联向量机（RVM）[41]，或者是支持向量机（SVM）[42-44]。同样流行的一种方法是将每一种行为/意图碎片式的嵌入一连串连续事件当中并使用隐马尔可夫模型（HMM）表征连续事件。不同事件间的转移概率可以学习数据获得，观测模型（例如不可观测事件和可得观测事件间的关系）也同样可以获得。对于新的观测序列，对比每一种HMM的观测值的可能性可以估计出行为/意图[24,25,45-47]。行为/意图估计的各种方法综合对比如表1所示。
表1 行为/意图估计的各种方法综合对比
b. 行为提取
预测轨迹与所识别的行为相匹配。通过对识别的行为派生出控制输入量，然后以运动学模型生成单条轨迹，这样便可以完成确定的行为识别[48]。这种严苛的确定方法的一个问题是不能考虑正在执行的行为或正要执行的行为时车辆当前状态的不确定性。为了探索以概率的形式执行一种潜在的操作，可以采用高斯过程或是快速随机采样树方法。从训练数据中可以学习到每一种行为的高斯过程，反过来，高斯过程可以用以以生成的方式为每一种行为创建样本轨迹[25,49]。另外，通过对车辆模型的输入空间采样，根据估计的行为/意图进行采样偏差，可以生成快速随机采样树[42]。这种方法的优点是为每一个行为产生一个可执行的动态轨迹。作为轨迹预测另一种方法，可达集用以描述车辆未来运动。表达方式可以是随机的[50]或是几何的[39]形式，如图7所示。
图7 三种行为提取方法：（a）RRT （b）高斯过程 （c）随机可达集
c. 方法的局限性
在实践中，对车辆的运动对立于其他车辆的假设是不成立的。各车辆共享路权，一辆车的行为势必影响其他车辆的行为。在道路交叉口的车辆内部关联更为强烈，优先级规则迫使车辆必须考虑其他车辆正在执行的行为。忽略这些依赖关系，会导致对情况的错误理解以及影响风险的评估。
4
感知/意识交互的运动模型
它认为交通参与者都是一个相互影响的行为实体，相比于前面描述的方法，在考虑他们之间的相互关系时，更能解释他们的运动。结果是有助于更好地理解环境，以及更可靠的风险评估。它们要么基于轨迹原型，要么基于动态贝叶斯网络。
4.1 基于轨迹原型的模型
对于依赖于轨迹原型的方法，车辆间的相互影响在学习期是难以考虑的，因为产生的大量运动模式会很快变得难以处理。但是，通过假设驾驶员在他们可以做到的条件下是有意识去避免碰撞的，那么，在匹配期间考虑相互间的影响时有可能的[51,52]。那些会导致不可避免的碰撞轨迹在匹配期间会加以限制。在用原型轨迹时考虑相互联系，这是一个简练的处理方式。由于车辆对另一车辆轨迹的影响难以直接建模，所以，原有的一些弊端在这种方式上仍然存在。
4.2 基于动态贝叶斯网络的模型
大部分感知/意识交互的运动模型是基于动态贝叶斯网络（DBN）。用耦合隐马尔可夫模型（CHMMs）可以对多运动实体的成对依赖关系进行建模[53]。由于成对依赖关系的数量会随实体的数量成平方增长。在复杂的交通情况下，复杂性是难以管理的。通过假设周围的交通会影响车辆的利益实现CHMMs的非对称可以简化模型[54]。依赖性的非对称假设大大地降低了计算的复杂度。自那起，该假设就在很多场景使用，特别是在换道超车[25]或跟车[55]。
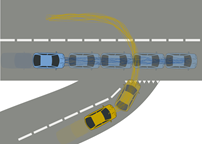
Agamennoni等人对车辆相互作用受到交通规则限制的事实进行了探索[56,57]。在以“次道车辆轨迹服从于主干道车辆轨迹”成对依赖关系的形式，多主体影响被分解为成对依赖的对数线性组合，如图8所示。
图8 感知/意识交互的运动模型（按照交通规则，黄车轨迹必须服从于蓝车轨迹）
最后，在一些工作中提出了跟踪车辆以及预测他们未来运动的一般概率框架。区别于对成对依赖关系建模，Gindele 等人提出的模型使用因式状态考虑相互影响[26]。车辆间的因果依赖关系描述为局部场景的函数，这降低了计算的复杂程度。在模拟的高速场景中验证了这一方法，但是，该方法理论上无法应用于其他交通场景。Lefevre等人用相似的方法对道路交叉口的车辆关联运动进行了建模[58-60]。但是，有别于直接对局部场景和驾驶员意图的建模，他们引入一个中间变量“预期行为”。在该模型中，场景影响驾驶员期望的行为，反过来会影响驾驶员的意图。这种方法在道路交叉口和真实乘用车的仿真中得到了验证。结果表明，当对交通状况推理时考虑车辆间的交互是有意义的，且对交叉口的风险评估也有作用。一般交通状况的泛化也有相应研究工作[60]。
4.3 方法的局限性
感知/意识交互的运动模型是目前所报道的最综合的方法。由于考虑了车辆的相互依赖关系，相比基于物理的运动模型，它具有更长时间预测能力；相比基于行为的运动预测，它具有更高的可靠性。但是，该方法也存在一些缺陷：计算成本高，不兼容实时的风险评估。所以，一些风险评估当中并不依赖于轨迹预测。
5、风险评估
关于风险，更为普适的一种解释是，源自于驾驶员非预期的操作的危险情况。
5.1 基于未来轨迹碰撞的风险
主要有两步：
- 预测场景中实体的未来可能轨迹。
- 对每一可能轨迹进行碰撞检测，并得出整体的碰撞风险。
a. 二值碰撞预测
碰撞检测可以是二值的。对于线性的基于物理的运动模型，求解运动学模型的线性微分方程可以得到特定时间下的车辆状态，对应的，两条轨迹的交点可以用快速的计算方法获得[11,13]。但是，一般情况下，对于闭环运动方程是非常复杂难以求解。一种解决办法是将轨迹分段成直线轨迹[17]。更为通用的做法是，离散化轨迹，迭代检查每一时间步长下的碰撞。碰撞检测简化为检测两点间的距离阈值[42]。考虑车辆外形，这个阈值可以由两个车辆外形的重合来取代。尽管确切的形状不是总能得到[2,6,7,21,25]或是可以用织机测试点表示[61]。如果车辆的不确定性可以获得，并且这种不确定性是高斯的，应用标准偏差的阈值可以用椭圆替代多边形[9,16]。为了简化交叉区域的计算量，椭圆可以由一些列圆替代[9]或是一系列点替代[16]。
一些驾驶辅助系统也专注于检测不可避免的碰撞。这是一种二值碰撞预测的特例，这里面，风险的值取为0或1依赖于是否存在一个驾驶员可以操作无碰行为。可以通过两种方式确定这样的操作是否可以完成。第一种方式是计算逃生操作（例如车辆该如何转向、制动、加速以避免碰撞）以及检查这些操作是否可行（可行是指这些操作不会超出车辆物理限制）[2]。第二种方法是考虑结合转向、制动和加速的整体，以及找到最优的避碰轨迹[7]。这个概念与应用在机器人中的不可避免的碰撞状态（ICS）极其相关[62]。
b. 碰撞概率预测
考虑未来运动的不确定性，碰撞风险可以通过概率的方式计算。在随机可达集的示例中，通过计算两车中心在同一单元的概率，并对所有可能单元组合，碰撞概率可以在离散的位置空间计算[22]。对于几何版本的可达集，碰撞概率可以通过计算未来车辆车辆位置几何形状的重叠度得到[39]。
对于当前状态的不确定性以正态分布的情况，随机线性化是一种解决方法[63]。当车辆未来的运动时以样本轨迹的概率分布表征时（典型的依赖于蒙特卡或者高斯过程的案例），风险的计算可以通过结合每一条未来可行轨迹的碰撞检测实现。这种方法在处理不确定性方面具有灵活性。例如，对于基于行为的运动模型，可以是对行为和所执行轨迹的求和，或者是假设行为已知，对所有可能的执行轨迹进行求和[25]。而且，根据最终采取的轨迹，可以计算与特定一辆车辆的碰撞风险或是对全部车辆求和获得全局的碰撞风险[25,52]。
c. 其他碰撞指标
通过深入分析预测轨迹和它们的交叉点，可以推导出一些能提供潜在碰撞信息的指标。流行的碰撞指标有临界速度[7,64]。代表车辆的形状的重叠程度[9]，两车同时占有冲突区域的概率[65]，以及碰撞的构型[9]。这些碰撞指标提供的信息可以确定减轻或是避免碰撞的最佳方法。
其他流行的风险指标是TTX（Time-to-X），其中，X表示的是有关碰撞的相关事件。
- TTC——Time-To-Collision：它可以作为什么样的行为应该采取（如果存在的话）的指示[2,6,9,15,66]。例如，在TTC还很长的时候，可以给驾驶员提供报警，而不是采取制动。在无人驾驶当中，TTC可以和最短制动时间对比，以决定何时采取制动[67]。对于驾驶警告运用，驾驶员的反应时间需要纳入考虑[13]。通过假设无人车直行一个特定轨迹的风险与最早的TTC成反比（计算所有可能轨迹的TTC），TTC可以作为识别风险最少的行为的工具[42]。
- TTR——Time-To-React：在难以避免的碰撞发生前，驾驶员还有多少时间可以用来操作。其思想来自于仿真每一种驾驶员操作的反应时间（例如转向，制动，加速），并用以识别在避免碰撞时该采取何种操作[11,48]。
5.2 基于意外行为的风险
它超出了避免碰撞风险的概念，考虑的是驾驶员执行意外操作的情感压力。例如，一辆在交叉口行进的车辆，只有很窄空间可以避免碰撞，但是大多数驾驶员认为这种情况是危险的，由于他们期望的是有更大的空间用于行驶。下面介绍两种方法：检测不寻常的事件和检测冲突的行为。
a. 检测不寻常的事件
在定义好车辆在道路上的正常行为后，通过检测那些不匹配正常行为的事件，可以估计该情况是否有风险。
一种直观的方法是定义一组规则，它根据场景描述了车辆正常的行为，并将任何异于正常的行为都定义为危险。当接近十字路口时，在可接受的速度上，规则可以是简单的启发式[68]，或是包含例如位置语义、天气条件或司机疲劳程度的更多先进概念[69]。然而，基于规则的系统存在不能考虑不确定性（数据或是模型）的局限性。
另一种手动定义正常行为的方法是对真实数据进行学习，得到道路使用这的典型行为。文献[70]采用一种高斯混合模型对正常行为学习。当前观测的可能性以当前情况是多么正常为衡量。例如闯红灯或是在禁止转向时转向的不正常行为通过检测这种可能性的阈值来识别。
b. 检测冲突的行为
预估驾驶员的驾驶意图，检测他们之间的潜在冲突，或者是与交通规则的冲突，来预测该情况是否有风险。
如果有足够的车辆违反交通规则的数据，通过特殊危险事件进行学习的模型对补充正常行为的模型是可行的。每一种模型归类为危险行为或是正常行为。检测危险行为转化成了分类问题，更能解释当前观测值的可能行为被选择。这种方法在文献[24]中实现了，使用雷达和相机记录了十字路口成千上万的真实轨迹。在数据中有大量违反了交通信号灯的有意义数据，这使得学习这种行为成为了可能。同样的，学习车辆完全遵守交通规则的数据可以得到正常模型。有两种分类方法在数据集中被验证和实现：带贝叶斯滤波的支持向量机（SVM-BF）和隐马尔可夫模型（HMM）。
对不止包含一辆车辆的交通场景，可以利用交通规则将行为对标注为冲突和不冲突。通过手动标注基于优先级规则的行为对，这种方法在道路交叉口的场景中得到实现[71,72]。冲突行为的方法近来普遍用于自动提取给定交通规则和当前情景下的期望驾驶员行为[59]。期望的行为与驾驶员意图对比便可以的到风险值。
6、附录
扩展卡尔曼滤波在处理非线性模型上有应用，它们在轨迹预测上的表现文献[73]有对比。更多关于概率滤波的信息可以参考文献[74]。
对那些对集群感兴趣的读者来说，Morris和Trivedi对最流行的方法做了一个全面的调研[75]。特别的，Buzan等人[37]、Hu等人[36]、Atev等人[29]专门研究了道路情景。
7、参考文献
参考文献可参考原文链接：
https://link.springer.com/content/pdf/10.1186%2Fs40648-014-0001-z.pdf
广告
最新资讯
-
燃料电池电堆冷启动测试
2024-04-26 09:03
-
某四驱电动车电磁噪声大问题优化
2024-04-26 08:53
-
丰田汽车副社长中嶋裕树一行到访国家智能网
2024-04-26 08:24
-
事关燃气汽车！燃气汽车分标委五项国家标准
2024-04-26 08:23
-
利用 NVIDIA AI Enterprise IGX 在边缘赋能
2024-04-26 08:17
广告
广告
