本篇围绕Fisher提出的数理统计学的第三类任务(也是最后一类任务)——抽样分布,展开初步的讨论,并借由抽样分布问题给出汽车耐久性工程和各行各业都面临的一个非常现实的问题,即最小样本量的确定。
1 什么是抽样分布
在《极大似然估计及点估计的一些重要性质》中我们已经谈到,统计量是“完全由样本所决定的量”,换句话说,统计量是样本的已知函数,因此,它也有其概率分布。统计量的概率分布称为(该统计量的)抽样分布。这里面,样本均值
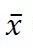
的抽样分布与最小样本量的确定密切相关。
2 Lindeberg-Levy中心极限定理与大样本法
Lindeberg-Levy在上世纪二十年代给出了如下重要而又非常有实用价值的中心极限定理:设X1,…,Xn共n个样本独立同分布于F,F有总体均值aF和总体方差σ2F,设0<σ2F<∞,以
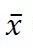
记样本均值
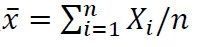
,则有
这里
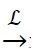
表示依分布收敛。Lindeberg-Levy中心极限定理告诉我们:样本均值
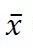
经过规则化后
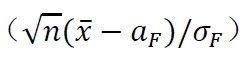
的极限分布为标准正态分布。
这里面有一点我们仔细琢磨琢磨是很牛的,就是Lindeberg-Levy中心极限定理并没有对总体分布F作任何限定。不管F服从什么分布,不管它是有参的还是非参的,甚至我们压根儿就不知道它是个什么分布,在这种一问三不知的情况下有一点我们却是可以肯定的,那就是F的抽样均值
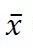
在规则化后服从标准正态分布!这种性质是样本均值的一个非常重要的大样本性质,称为渐进正态性。
我们在此再次扔一扔筛子,来帮我们理解和体会一下Lindeberg-Levy中心极限定理的“威力”。我们拿来一对筛子,投掷一次,计算和记录一下两个筛子的点数之和。如图1所示,把这个过程重复100次、1000次和10000次,我们发现两个筛子点数和的分布(即样本均值
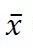
的抽样分布),越来越接近于完美的正态分布。您可能会说,筛子的分布我已经知道了呀?不是均匀分布么?那好,您可以再去找来任何一对被做过手脚的筛子,重复上面的试验,结果你会发现,点数和的分布仍然会越来越接近于完美的正态分布,只不过由于筛子被做过手脚了(因此这回我们可真是压根儿就不知道它服从什么分布),因此最后最经常出现的点数和不见得是7罢了。
图1 通过掷筛子来验证Lindeberg-Levy中心极限定理1
有了Lindeberg-Levy中心极限定理,我们可以在样本量比较大的时候对于
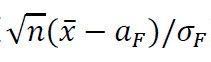
不超过某一值
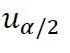
的概率进行一个近似的估算,其中
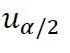
为标准正态分布的上α/2分位点,即:
对于上式,我们有两点解释:
1)γ称为置信度,这是区间估计里面的一个重要概念。
区间估计就是用一个区间去估计未知参数,即把未知参数值估计在某两界限之间,相对于点估计来说,区间估计的一个明显的好处是把可能的误差醒目的标识了出来。
比如说,假设鸡蛋的重量是一个服从正态分布的随机变量,通过《极大似然估计及点估计的一些重要性质》中介绍的极大似然估计法,我们可以得到鸡蛋重量的样本均值,比方说50g。但是,这个点估计评估结果没有给出评估的精度。区间估计的结果表示方式是,鸡蛋重量落在某一数值区间的概率是多少。这里面有两个要素:第一,数值区间的长度,我们把这个因素称为精度;第二,落在这个区间的概率,我们把他称为置信度,是可靠性的一种表征。
置信度和精度是一对矛盾的因素。比方说,我们可以自信的说,鸡蛋重量落在数值区间[0吨,1吨]的置信度是100%。这个评估结果很可靠,置信度很高,但是评估结果却没有什么用处,因为精度太低。反之亦然。
区间估计理论就是提供用统计学的方法解决置信度和精度之间的矛盾,把一定的置信度与一定的精度关联起来。现在最流行的一种区间估计理论是美国统计学家J. Neyman在本世纪30年代建立的。
2)总体标准差
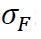
是未知的,但是在《极大似然估计及点估计的一些重要性质》我们谈到,样本标准差S是
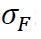
的一个相合估计,因此在样本量比较大的时候,可以用S去代替
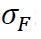
。
这样,上式变化为
式(1)对于最小样本量的确定是及其重要的。我们想抽取一定数量的样本,用样本均值
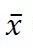
来估计总体均值aF,但是希望两者足够接近。如果定义
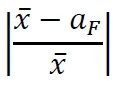
为相对偏差的话,我们希望相对偏差不要超过某一指定的值δ。因此,由式(1)得到
因此,当指定相对偏差为δ,置信度为γ时,最小样本量为
由式(2)我们看到,影响最小样本量大小的有三方面的因素:
1)置信度的因素。如果我们要求统计结果越可靠,置信度越高,相应的
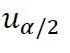
的值就会增大,从而引起最小样本量的增大。
2)相对偏差的因素。如果我们希望样本均值越来越精确的逼近总体均值,没有别的途径,唯有增加最小样本量。
3)随机变量本身的变异性。式(2)中

是一个非常重要的量,称为变异系数,反应样本标准差和样本均值之间的相对关系。如果变异系数越大,说明我们所研究的随机变量的变异性越大,在这种情况下,需要更多的样本量来达到同等的置信度和相对偏差。
以上介绍的最小样本量的确定方法,来源于Lindeberg-Levy中心极限定理,是一种大样本方法。它有一个好处:我们可以在对样本分布一无所知的情况下使用这一方法来进行最小样本量的确定。但是,这里面也存在一个问题,那就是,Lindeberg-Levy中心极限定理,以及牵扯到的样本标准差的相合性,都是大样本性质,也就是说,是在样本量n趋于无穷大的时候才严格成立的?事实上样本量不可能无穷大,当样本量固定在某一个值的时候,相关定理都是近似成立的。更加让人遗憾的是,这种近似产生的偏差到底有多少,统计学大样本理论发展到今天,还没有能够给出合理的解释。因此,这种方法(特别是对于处女座的工程师来说)用起来总是有些感觉不踏实。
3 t分布与小样本法
1908年,英国统计学家W.S. Gosset很文青的以“Student”作为笔名,发现和发表了一个统计学中最重要的分布之一,t分布,这是统计学发展过程中的一件大事,开创了统计学小样本法的先河。W.S. Gosset证明:
如果已知总体服从正态分布,但是其总体均值aF和总体方差σ2F未知,那么从总体中抽样本X1,…,Xn,则
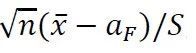
服从(n-1)自由度的t分布。
与Lindeberg-Levy中心极限定理相比,上面的定理对于应用的条件有所加强,也就是说不能对总体的分布情况一无所知,而是总体必须服从正态分布,因此,这使得上述定理的应用范围有所限制。但是,好在总体服从正态分布的情况是非常多见的,比如说,在《车辆耐久性工程中的重要随机变量及如何确定其服从怎样的分布模型》一文中我们提到,车辆耐久性工程中的重要随机变量“车辆累积行驶里程达到设计里程时车辆某处的某载荷对应的伪损伤(或伪损伤密度,或等效载荷幅值,……)”就服从对数正态分布,因此上述定理仍然有很广阔的应用空间。但是,应用条件的些许限制,却换来了一个很大的优点,那就是应用该定理的时候样本量不需要趋于正无穷定理才成立,换句话说,当样本量固定为一个有限的数值时,相关定理是严格成立的!
基于以上定理,采用与第2小节完全相同的步骤,可以得到当总体服从正态分布时,对应于相对偏差为δ,置信度为γ的最小样本量为
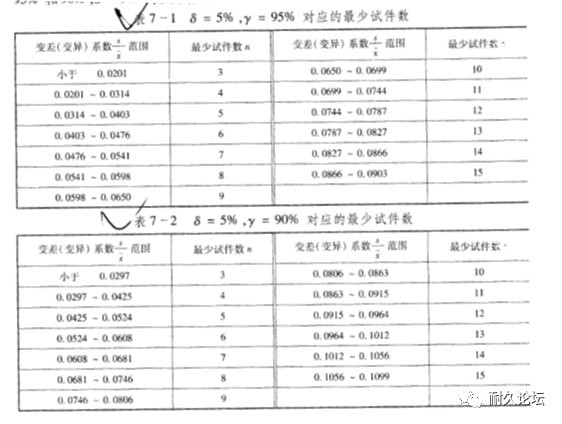
再次强调,当总体服从正态分布式,式(3)是精确解。在实际工程中,经常取δ=5%,γ=95%,或δ=5%,γ=90%。图2会是一个经常用到的表格,超出表格范围的可以找相关软件计算。
图2 采用式(3)计算最小样本量时的常用表格2
4 老王到底要在高速路上跑多远才能回家吃饭
随机变量Y=司机老王驾车在高速路上每行驶10km时车辆某处某载荷对应的伪损伤(或伪损伤密度,或等效载荷幅值,……)。
为了回答什么时候回家吃饭的问题,让老王先在高速路上开上100km,获得10个样本Yi,i=1,…,10。在《车辆耐久性工程中的重要随机变量及如何确定其服从怎样的分布模型》我们提到,随机变量Y服从对数正态分布,因此,满足采用小样本法、使用式(3)的条件。在指定了相对偏差为δ,置信度为γ,我们可以由式(3)清楚的知道:老王是不是已经可以收工了;如果不能收工,还得开多远(具体地说是几个10km)。
至此,我们已经用连续的三篇文章《车辆耐久性工程中的重要随机变量及如何确定其服从怎样的分布模型》、《极大似然估计及点估计的一些重要性质》和《道路试验啊!这到底要开多远才是个头?——抽样分布与最小样本量的确定》讨论了Fisher先生给出的数理统计学的三大任务:定模型、估计和抽样分布。这三篇文章虽然不长,但是选择性的围绕Fisher先生提出的这三大问题,把经典统计学范畴内的相关重要成果加以介绍,已经使我们可以对于一维随机变量做不少统计处理。
下一篇文章中,我们将简要介绍西门子工业软件公司的核心专利技术,客户相关(Customer Correlation,简称CuCo)的车辆道路载荷大数据获取和分布模型的构建技术。我们将看到,运用CuCo技术获取大数据后,我们可以在一维随机变量的范围内,用现在已经介绍的这一些统计学知识,很好的解决车辆耐久性工程中载荷分布模型的确立,这一最重要的顶层输入问题。
参考文献
1. 统计学,David Freedman, Robert Pisani, Roger Purves, Ani Adhikari,1997年10月,第一版,中国统计出版社.
2. 刘文珽,结构可靠性设计手册,2008年2月,第一版,国防工业出版社.
附录:W.S. Gosset(1876—1937),英国统计学家。
作者简介:李旭东,2003年毕业于大连理工大学机械工程学院,获工学学士学位;2008年毕业于北京大学力学系固体力学专业,获理学博士学位。2008年至2014年,就职于中国航空综合技术研究所,历任工程师、高级工程师;2015年至今,就职于西门子工业软件(北京)有限公司,任职耐久性应用工程师。长期专注于(金属)材料和结构耐久性和损伤容限分析方法研究。
作者个人微信号:lixudong2008 (添加微信号请注明“姓名+工作单位”)
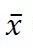 的抽样分布与最小样本量的确定密切相关。
的抽样分布与最小样本量的确定密切相关。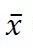 记样本均值
记样本均值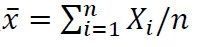 ,则有
,则有
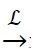 表示依分布收敛。Lindeberg-Levy中心极限定理告诉我们:样本均值
表示依分布收敛。Lindeberg-Levy中心极限定理告诉我们:样本均值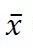 经过规则化后
经过规则化后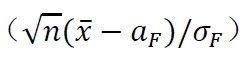 的极限分布为标准正态分布。
的极限分布为标准正态分布。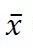 在规则化后服从标准正态分布!这种性质是样本均值的一个非常重要的大样本性质,称为渐进正态性。
在规则化后服从标准正态分布!这种性质是样本均值的一个非常重要的大样本性质,称为渐进正态性。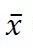 的抽样分布),越来越接近于完美的正态分布。您可能会说,筛子的分布我已经知道了呀?不是均匀分布么?那好,您可以再去找来任何一对被做过手脚的筛子,重复上面的试验,结果你会发现,点数和的分布仍然会越来越接近于完美的正态分布,只不过由于筛子被做过手脚了(因此这回我们可真是压根儿就不知道它服从什么分布),因此最后最经常出现的点数和不见得是7罢了。
的抽样分布),越来越接近于完美的正态分布。您可能会说,筛子的分布我已经知道了呀?不是均匀分布么?那好,您可以再去找来任何一对被做过手脚的筛子,重复上面的试验,结果你会发现,点数和的分布仍然会越来越接近于完美的正态分布,只不过由于筛子被做过手脚了(因此这回我们可真是压根儿就不知道它服从什么分布),因此最后最经常出现的点数和不见得是7罢了。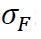
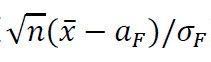 不超过某一值
不超过某一值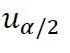 的概率进行一个近似的估算,其中
的概率进行一个近似的估算,其中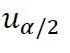 为标准正态分布的上α/2分位点,即:
为标准正态分布的上α/2分位点,即: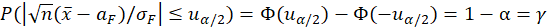
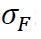 是未知的,但是在《极大似然估计及点估计的一些重要性质》我们谈到,样本标准差S是
是未知的,但是在《极大似然估计及点估计的一些重要性质》我们谈到,样本标准差S是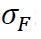 的一个相合估计,因此在样本量比较大的时候,可以用S去代替
的一个相合估计,因此在样本量比较大的时候,可以用S去代替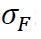 。
。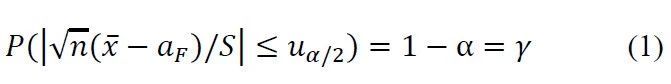
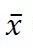 来估计总体均值aF,但是希望两者足够接近。如果定义
来估计总体均值aF,但是希望两者足够接近。如果定义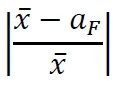 为相对偏差的话,我们希望相对偏差不要超过某一指定的值δ。因此,由式(1)得到
为相对偏差的话,我们希望相对偏差不要超过某一指定的值δ。因此,由式(1)得到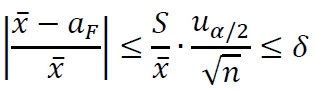
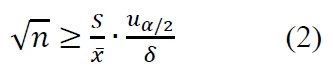
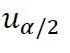 的值就会增大,从而引起最小样本量的增大。
的值就会增大,从而引起最小样本量的增大。 是一个非常重要的量,称为变异系数,反应样本标准差和样本均值之间的相对关系。如果变异系数越大,说明我们所研究的随机变量的变异性越大,在这种情况下,需要更多的样本量来达到同等的置信度和相对偏差。
是一个非常重要的量,称为变异系数,反应样本标准差和样本均值之间的相对关系。如果变异系数越大,说明我们所研究的随机变量的变异性越大,在这种情况下,需要更多的样本量来达到同等的置信度和相对偏差。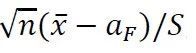 服从(n-1)自由度的t分布。
服从(n-1)自由度的t分布。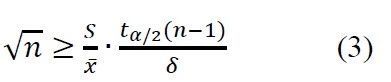






 广告
广告





























































