Proceedings of the 37th Chinese Control Conference
July 25-27, 2018, Wuhan,
作者:李晏,张榜,陈辛波,杭鹏
摘要:四轮独立转向电动车(4WIS EV)具有低速机动性强、高速稳定性好的特点,是一种理想的智能型车辆。解决车辆的轨迹跟踪控制问题是实现智能化交通的重要组成部分,本文针对4WIS EV,基于模型预测控制(MPC)算法进行了路径跟踪控制研究。
首先,基于简化的二自由度车辆动力学模型,对4WIS EV在四轮转向模式下的稳态转向进行几何学分析,并推导出车辆质心侧偏角为零时前轮转角与后轮转角的几何关系;再者,基于车辆运动学模型,设计了采用MPC算法的路径跟踪控制器,为提高车辆跟踪过程中的稳定性和准确性,对车辆前后轮转角进行主动转向控制。最后,为了验证所设计模型预测控制器的有效性和可靠性,选择成熟的商用动力学仿真软件Carsim与Matlab/Simulink构建联合仿真平台,以低速泊车为工况,在不同的行驶速度和设计参数下进行仿真,结果表明所设计的MPC算法具有良好的鲁棒性和可靠性。
关键词: 四轮独立转向, 电动车, 模型预测控制, 路径跟踪
1 引言
随着车辆主动安全技术的快速发展,自动驾驶技术已成为智能交通系统研究的热点问题。路径跟踪是地面自主车辆的基本能力与首要任务,目前对无人驾驶汽车的研究大多基于传统的内燃机,少量企业如特斯拉等对电动汽车展开智能驾驶研究,汽车电动化是未来的发展趋势,电动汽车的智能化更是大势所趋。四轮独立转向电动车( 4WIS EV )是一种具有多执行器、多控制自由度的特殊车辆,具有可控自由度大、机动性和稳定性高等特点,四个车轮的转向均可单独控制,可实现主动前后轮控制、直接横摆力矩控制等,是一种理想的无人驾驶汽车车型 [1-2] 。 路径跟踪要求跟踪误差尽可能小,目前路径跟踪控制算法主要有最优控制、 PID 控制、滑模控制、鲁棒控制、模糊控制、模型预测控制等 [3-7] 。 PID 控制简单实用,但对车辆特性变化的鲁棒性不强;而最优控制和鲁棒控制等方法,控制算法设计复杂,不易在控制器中实现,且算法对模型的精度依赖性高。而模型预测控制( MPC )是一种基于简单模型进行滚动优化控制的算法,相比于其他控制方法,模型预测控制最明显的优点是对模型的精度要求不高,且能在控制过程中增加多种约束,通过目标函数可同时控制多个系统变量 , 具有建模直观、动态响应快等优点,在车辆控制领域上有着比较广泛的应用 [8] 。本文以 4WIS EV 为研究对象,建立了其在低速行驶时的运动学模型。其次,基于模型预测控制算法,设计了一种在多个非线性约束条件下的路径跟踪控制器,轨迹跟踪过程中只对车辆的前后轮转角进行控制,而保持车辆的纵向速度不变,通过 Matlab/Simulink 与 Carsim 联合仿真,验证了所设计控制算法在不同行驶工况和设计参数下的路径跟踪性能,仿真结果表明所设计的 MPC 算法具有良好的鲁棒性和可靠性。
2 四轮独立转向电动车系统建模
本文以一种新型 4WIS EV样车为研究对象,如图1所示,该车主要由四组下图2所示的一体化线控独立转向/驱动模块所组成,该模块集成了悬架系统、驱制动系统和转向系统,如图3所示。一体化线控独立转向/驱动模块的搭载使得该车四个车轮的转向角度都独立可控,控制冗余自由度更多,控制策略选择更具多样化,更有利于发挥出色的动力学性能,整车参数如表1所示。
图1: 4WIS EV 样车 图2: 一体化模块
转向模块 悬架模块 驱动模块
图3: 一体化线控独立转向/驱动模块
表1.整车参数
2.1 几何学分析与动力学模型
如图 4 所示是车辆简化单轨模型,由转向过程中车轮转角满足 Ackerman 转角定律,推导得出车辆实际四个车轮的转角
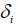
( i=fl,fr,rl,rr 分别表示前左轮、前右轮、后左轮、后右轮)与单轨模型前后转角(
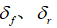
)之间的关系可表述为
由于所设计的控制器是对轨迹跟踪过程中的前轮偏角进行主动控制,因此需要确定四轮转向模式下,
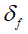
与
的关系,
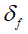
与

之间的关系可表示为
欲确定不同车速下的值,首先需要建立包含质心侧偏角和横摆角速度在内的车辆二自由度运动方程。基于小角度假设,四轮转向稳态下各轮胎的侧偏角为
其中
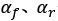
分别为各轮胎的侧偏角,
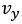
为车辆侧向速度,
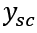
为车辆纵向速度,r 为横摆角速度。推导可得出二自由度模型的运动方程为
同时,质心侧偏角满足
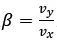
,整理可得
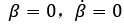
(5)
采取转向过程中车辆横摆角速度r不变、质心侧偏角为零的控制策略,即:
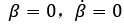
且
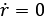
,带入上式结合( 3 )、( 4 )可求得
图 4: 四轮转向车辆单轨道模型
2.2 运动学模型
运动学模型的建立主要用于设计路径跟踪控制器,当车辆以低速行驶时,其运动学方程可表示为
式中X、Y分别为车辆在大地坐标系下的横纵坐标,
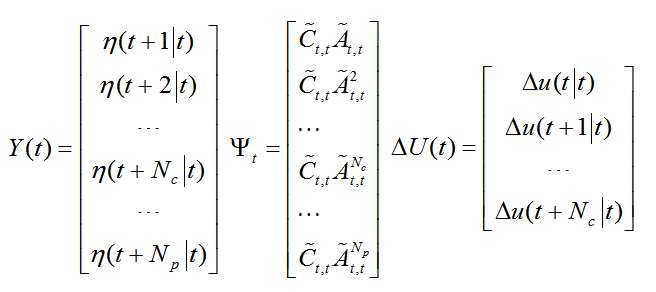
为车辆横摆角,
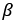
为质心侧偏角,v为车速,
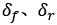
分别为单轨模型前后车轮的转角,考虑低速行驶时,质心侧偏角
较小,
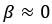
,可进一步简化运动学模型,式(7)可表示为如下形式
考虑式(7)所建立的非线性运动学模型,当车速恒定时,前后轮转角关系确定时,系统可以被看做一个输入量为
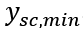
,状态量为
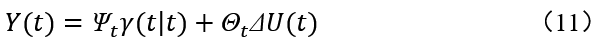
的控制系统,其一般形式为
该车辆运动学模型是一个非线性系统,不能直接用于线性时变模型预测控制,因此首先需要对非线性模型进行线性化,本文采用针对状态轨迹的线性化方法,即通过对系统施加持续不变的控制量,得到一条状态轨迹,根据该状态轨迹和实际状态量的偏差设计线性模型预测控制算法。得到线性时变方程为
(8)式中
对式(8)采用一阶差商的方法进行离散化处理,得出离散的状态空间表达式
式中:
3 控制器设计
本文基于模型预测控制算法进行路径跟踪控制器设计,图5所示为所设计的控制系统结构图,MPC控制器的输入量为参考的
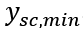
以及车辆实际
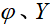
,输出量为前轮转角
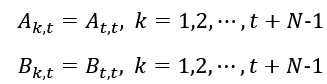
,根据4WIS EV转向几何学推导得出四个车轮转角作为非线性4WIS EV模型的输入量并反馈回实际的
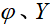
作为MPC的输入量。
图 5: 4WIS EV控制系统结构图
对式(9)做如下转换:
得到一个新的状态空间表达式
式中:
n、m分别为状态量和控制量维度。为简化计算,做如下假设
推导可得出系统的预测输出表达式:
式中:
为了避免控制器在实际执行过程中,无法得到最优解的情况,有必要在目标函数中加入松弛因子,在设计轨迹跟踪控制器时,采用如下形式的目标函数
式中
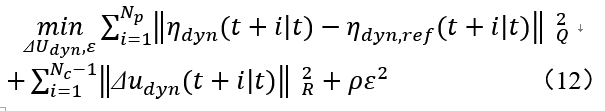
,Np和Nc分别是预测时域和控制时域,
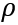
为权重系数,
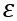
为松弛因子,Q和R为权重矩阵,基于运动学模型的主动转向跟踪控制器在每个控制周期内要解决的优化问题可表示为:
约束条件为
式中,
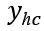
为硬约束输出,
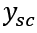
为软约束输出,
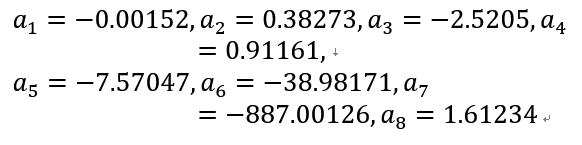
和
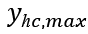
为硬约束极限值,
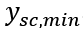
和
为软约束极限值。在每个控制周期内完成对(12)式的求解后,得到控制时域内的一系列控制输入增量和松弛因子:
将该控制序列中的第一个元素作为实际的控制输入增量作用于系统,即
进入下一个控制周期后,重复上述过程,如此循环实现对期望轨迹的跟踪控制。
4 Carsim/Simulink联合仿真
4.1 参考轨迹描述
为了验证控制算法的可行性与准确性,基于 Carsim 车辆模型,设计了在不同车速和控制器设计参数下的仿真工况,采 Matlab/Simulink 与 Carsim 软件进行联合仿真。参考轨迹采用文献 9 中的反正切与多项式组合函数,具体算式和轨迹图如下所示 :
其中,
图 6: 参考轨迹
4.2 控制器设计
跟踪控制算法相关参数值设置如下
表2.算法参数值
所设计的主动转向跟踪控制器是以车辆前轮偏角作为控制器的输入,控制目标是通过不断减少与参考轨 迹的偏差,跟踪参考轨迹,为了更加全面的分析所设计控制方法的可行性,分别在不同的车速和预测及控 制时域下进行仿真分析,如图7所示是基于Carsim/Simulink的联合仿真平台。
图 7: Carsim/Simulink仿真平台
(1)不同速度下的仿真分析
模型预测控制器可以根据建立的车辆模型预测系统未来的输出,应对车速的变化具有很强的鲁棒性。主动转向控制仿真实验分别在2m/s、3m/s、4m/s的速度下进行,控制器所采取的参数如上表所示,其中预测与控制时域选取
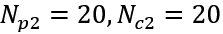
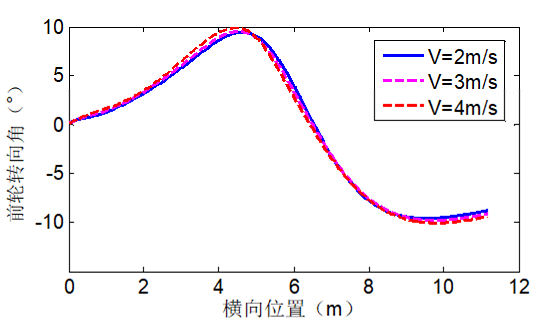
,以Carsim车辆模型作为模型预测控制的预测模型,仿真工况1的仿真结果如下图8-13所示。图8、9为3种车速下车辆的轨迹跟踪效果,由仿真结果可知,在相同的控制参数下,不同的车速行驶工况都具备良好的轨迹跟踪性能,而在相同的控制器参数下,随着速度的增大,跟踪误差呈正相关性,说明该控制器对低速行驶工况的鲁棒性更强。图10是跟踪过程中的纵向位置和横摆角误差值,三种速度下纵向位置最大误差值为0.0542m(4m/s),考虑系统建模影响,该误差在合理范围内,可满足路径跟踪要求,体现了该控制算法对速度具有很强的鲁棒性。图11、12分别为4WIS EV前后轮控制转角,在整个过程中,车轮转角变化量都在一定的范围内,没有出现转角控制量突变的情况,同时前后轮转向角反向且满足一定的比例关系,满足4WIS EV在低速行驶时的转向几何关系。图13是控制器计算的前轮转角增量,观察可知,跟踪过程中控制增量没有突变的现象,每个控制周期内的控制增量都保持在约束范围内,表明车辆行驶过程非常平稳。
图 8: 不同速度下的纵向位置跟踪效果及放大图
图 9: 不同速度下的横摆角跟踪效果
图10: 不同速度下的跟踪误差
图11: 前轮转向角
图 12: 后轮转向角
图 13: 不同速度下的前轮转向角控制增量
(2)不同设计参数下的仿真分析
参数设定对控 制器性能有很大的影响,对于 MPC 算法来说,最重要的设计参数就是预测时域和控制时域,为了验证不同时域对控制器跟踪性能的影响,在行驶速度为v=3m/s 时,设计了三种不同参数的控制器 A 、 B 、 C ,其中 A 、 B 、 C 各时域分别设置如下:
仿真结果如图所示,其中图 14 、 15 为两个控制器跟踪期望轨迹的对比,从图 14 、 15 可以看出,控制器 A 、 B 可以很好的跟踪期望轨迹,而控制器 C 虽能跟踪期望轨迹,但相比于 A 、 B 其跟踪误差相对较大,这是因为控制器 C 的预测时域和控制时域更小,由此可知,增大预测时域和控制时域可有效的改进控制器性能,但控制器 C 也有自身的优势,采用较小的预测时域和控制时域的可以有效的提升系统的实时性,图 16 反映了在不同的设置参数下控制器的计算时间。图 17 为在三种不同参数的控制器下的跟踪误差,纵向位置和航向角误差都保持在较小的范围内。
图 14: 不同设计参数下的纵向位置跟踪效果
图 15: 不同设计参数下的横摆角跟踪效果
图 16: 不同设计参数下的控制器计算时间
图 17: 不同设计参数下的的跟踪误差
5 结论
本文针对一种新型4WIS EV设计了一种基于模型预测控制算法的路径跟踪控制器,采用对车辆前后轮转角进行主动转向控制搭建了基于Carsim与Matlab/Simulink联合仿真平台,以低速泊车为工况,在不同的行驶速度和设计参数下进行仿真,仿真结果表明,所设计的模型预测控制器对速度和设计参数都具有很强的鲁棒性,但仍存在较小的跟踪误差,并且仿真结果表明在速度较高以及预测时域和控制时域较小时,跟踪误差更加明显,说明所设计的控制器更适用于速度较低的工况,这与控制器所采用的模型为 低速运动学模型特性相吻合。另外分析可知,跟踪误差来源主要是模型预测控制器是以简化 4WIS EV 运动学模型作为预测模型,未考虑系统未建模影响,这与实际的 Carsim 车辆模型具有一定的偏差;同时,在对非线性运动学模型进行线性化时,引进了一定的模型误差。
END
参考文献
[1] HANG P, CHEN X, FANG S, et al.Robust control forfour-wheel-independent-steering electric vehicle withsteer-by-wire system [J]. InternationalJournal of AutomotiveTechnology, 2017, 18(5): 785−797.
[2] HANG P,CHEN X, LUO F, et al. Robust Controlof a Four-Wheel-Independent-Steering Electric Vehicle for PathTracking[J].SAEInternational Journal of Vehicle Dynamics,Stability, and NVH, 2017, 1(2):307−316.
[3] 丁延超, 丁能根, 袁玮. 基于四轮主动转向的路径跟踪自动控制[J]. 汽车技术, 2011(7): 24−27.
[4] HIRAOKA T,NISHIHARA O, KUMAMOTO H. Automatic path-tracking controller of a four-wheelsteering vehicle [J].Vehicle System Dynamics, 2009, 47(10): 1205−1227.
[5] MASHADI B,AHMADIZADEH P, MAJIDI M, et al.Integrated robust controller for vehicle path following[J].Multibody System Dynamics, 2015, 33(2): 207−228.
[6] LAUFFENBURGER J,BASSET M, COFFIN F, et al.Driver-aid system using path-planning for lateralvehicle control [J]. Control Engineering Practice, 2003, 11(2):217−231.
[7] SHIM T, ADIREDDY G, YUAN H. Autonomousvehiclecollision avoidance systemusing path planning andmodel-predictive-control-basedactive front steering and wheeltorquecontrol [J]. Proceedings of the Institution ofMechanicalEngineers Part D Journal of AutomobileEngineering, 2012,226(6): 767−778.
[8] 王艺, 蔡英凤, 陈龙, 王海, 李健, 储小军.基于模型预测控制的智能车辆路径跟踪控制器设计[J].汽车技术, 2017(10):44-48.
[9] LI Hong, GUOKonghui, SONG Xiaolin, LI Feilong,”Trajectory planning ofautomatic parallel parking with multi-constraints based on Matlab”,Journal ofCentral South University (Science and Technology),44(1),2013-01.
联系人:李老师
电话:021-69589225
邮箱:11666104@tongji.edu.cn

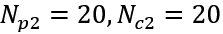

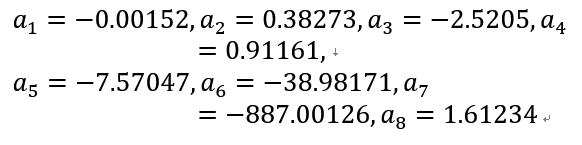


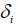 ( i=fl,fr,rl,rr 分别表示前左轮、前右轮、后左轮、后右轮)与单轨模型前后转角(
( i=fl,fr,rl,rr 分别表示前左轮、前右轮、后左轮、后右轮)与单轨模型前后转角(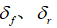 )之间的关系可表述为
)之间的关系可表述为
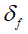 与
与 的关系,
的关系,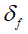 与
与 之间的关系可表示为
之间的关系可表示为

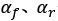 分别为各轮胎的侧偏角,
分别为各轮胎的侧偏角,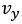 为车辆侧向速度,
为车辆侧向速度,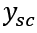 为车辆纵向速度,r 为横摆角速度。推导可得出二自由度模型的运动方程为
为车辆纵向速度,r 为横摆角速度。推导可得出二自由度模型的运动方程为
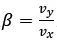 ,整理可得
,整理可得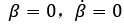 (5)
(5)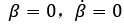 且
且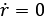 ,带入上式结合( 3 )、( 4 )可求得
,带入上式结合( 3 )、( 4 )可求得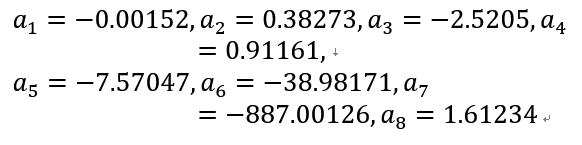


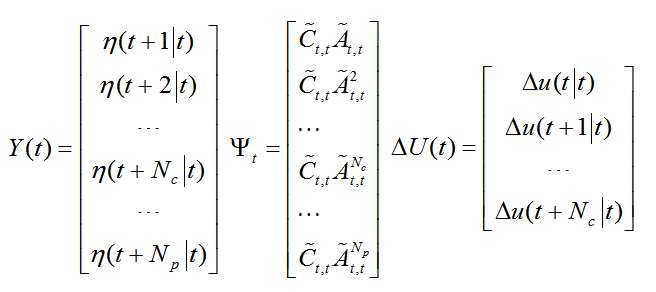 为车辆横摆角,
为车辆横摆角,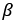 为质心侧偏角,v为车速,
为质心侧偏角,v为车速,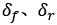 分别为单轨模型前后车轮的转角,考虑低速行驶时,质心侧偏角
分别为单轨模型前后车轮的转角,考虑低速行驶时,质心侧偏角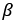 较小,
较小,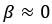 ,可进一步简化运动学模型,式(7)可表示为如下形式
,可进一步简化运动学模型,式(7)可表示为如下形式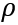
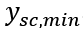 ,状态量为
,状态量为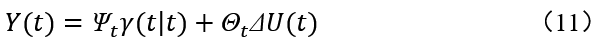 的控制系统,其一般形式为
的控制系统,其一般形式为
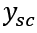



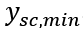 以及车辆实际
以及车辆实际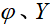 ,输出量为前轮转角
,输出量为前轮转角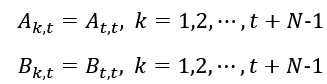 ,根据4WIS EV转向几何学推导得出四个车轮转角作为非线性4WIS EV模型的输入量并反馈回实际的
,根据4WIS EV转向几何学推导得出四个车轮转角作为非线性4WIS EV模型的输入量并反馈回实际的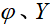 作为MPC的输入量。
作为MPC的输入量。



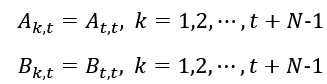
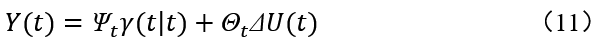
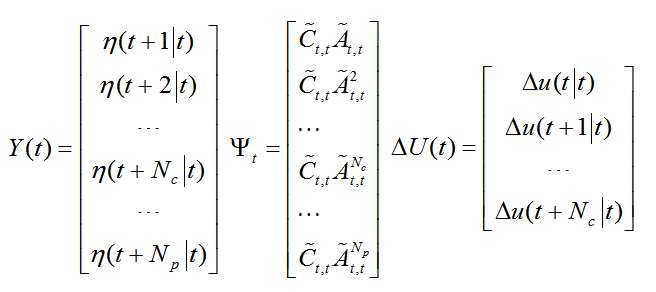


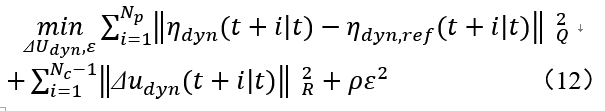 ,Np和Nc分别是预测时域和控制时域,
,Np和Nc分别是预测时域和控制时域,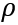 为权重系数,
为权重系数,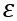 为松弛因子,Q和R为权重矩阵,基于运动学模型的主动转向跟踪控制器在每个控制周期内要解决的优化问题可表示为:
为松弛因子,Q和R为权重矩阵,基于运动学模型的主动转向跟踪控制器在每个控制周期内要解决的优化问题可表示为: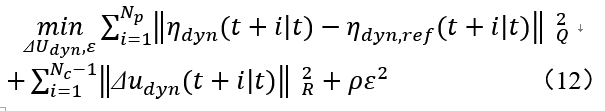

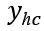 为硬约束输出,
为硬约束输出,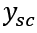 为软约束输出,
为软约束输出,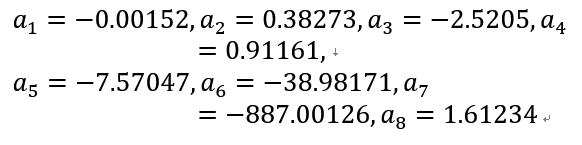 和
和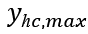 为硬约束极限值,
为硬约束极限值,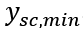 和
和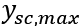 为软约束极限值。在每个控制周期内完成对(12)式的求解后,得到控制时域内的一系列控制输入增量和松弛因子:
为软约束极限值。在每个控制周期内完成对(12)式的求解后,得到控制时域内的一系列控制输入增量和松弛因子:


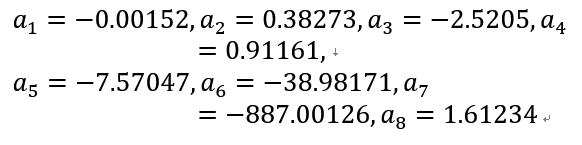



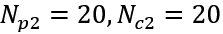 ,以Carsim车辆模型作为模型预测控制的预测模型,仿真工况1的仿真结果如下图8-13所示。图8、9为3种车速下车辆的轨迹跟踪效果,由仿真结果可知,在相同的控制参数下,不同的车速行驶工况都具备良好的轨迹跟踪性能,而在相同的控制器参数下,随着速度的增大,跟踪误差呈正相关性,说明该控制器对低速行驶工况的鲁棒性更强。图10是跟踪过程中的纵向位置和横摆角误差值,三种速度下纵向位置最大误差值为0.0542m(4m/s),考虑系统建模影响,该误差在合理范围内,可满足路径跟踪要求,体现了该控制算法对速度具有很强的鲁棒性。图11、12分别为4WIS EV前后轮控制转角,在整个过程中,车轮转角变化量都在一定的范围内,没有出现转角控制量突变的情况,同时前后轮转向角反向且满足一定的比例关系,满足4WIS EV在低速行驶时的转向几何关系。图13是控制器计算的前轮转角增量,观察可知,跟踪过程中控制增量没有突变的现象,每个控制周期内的控制增量都保持在约束范围内,表明车辆行驶过程非常平稳。
,以Carsim车辆模型作为模型预测控制的预测模型,仿真工况1的仿真结果如下图8-13所示。图8、9为3种车速下车辆的轨迹跟踪效果,由仿真结果可知,在相同的控制参数下,不同的车速行驶工况都具备良好的轨迹跟踪性能,而在相同的控制器参数下,随着速度的增大,跟踪误差呈正相关性,说明该控制器对低速行驶工况的鲁棒性更强。图10是跟踪过程中的纵向位置和横摆角误差值,三种速度下纵向位置最大误差值为0.0542m(4m/s),考虑系统建模影响,该误差在合理范围内,可满足路径跟踪要求,体现了该控制算法对速度具有很强的鲁棒性。图11、12分别为4WIS EV前后轮控制转角,在整个过程中,车轮转角变化量都在一定的范围内,没有出现转角控制量突变的情况,同时前后轮转向角反向且满足一定的比例关系,满足4WIS EV在低速行驶时的转向几何关系。图13是控制器计算的前轮转角增量,观察可知,跟踪过程中控制增量没有突变的现象,每个控制周期内的控制增量都保持在约束范围内,表明车辆行驶过程非常平稳。















 广告
广告





























































