本篇文章将借助双干涉模型,详述(道路)载荷分布这一顶层输入对于(车辆)耐久性工程下游的设计工作和试验工作的指引作用,借此阐述和强调(道路)载荷分布对于(车辆)耐久性工程的全局性和战略性作用。
1、双干涉模型
双干涉模型是可靠性工程中非常实用和重要的一个模型,在车辆耐久性工程中同样发挥着重要的作用。我们首先约定,尽管在表征相对损伤的时候我们有不少大同小异的量值可以选择,但是,为了在讨论今天这个话题时理解起来更方便,图1中的横轴我们选取为“等效载荷幅值的对数”。之所以还要取一个对数,是因为我们认为等效载荷幅值服从对数正态分布,取对数后容易处理。
图1 双干涉模型1
1.1 载荷分布——借助CUCO已经搞定
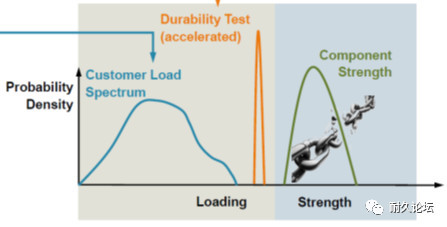
双干涉模型的“左翼”——载荷分布,借助上一篇文章《客户相关的道路载荷大数据获取和道路载荷分布模型的构建》介绍的西门子工业软件公司的CUCO核心专利技术体系,已经解决。与载荷分布相关的量值,我们都用下脚标L(Load,载荷)予以标识。比如载荷分布中,等效载荷幅值对数的样本均值为
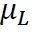
,样本方差为
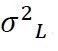
,等效载荷幅值的中位数为L0.50=exp(
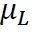
),等等。借助CUCO,这些个数值目前我们都有了。
1.2 强度分布——对企业质量管理体系和水平的考验
某OEM从某零部件供应商购进(比如说)排气系统。从耐久性方面说,排气系统的质量怎么样?质量是否稳定?这需要OEM企业的相关部门进行按时的抽样检验。
假设在一个批次的抽样中,一共抽取了n个样本。我们把这n个样本,逐一放在疲劳试验机上按照相关的试验规程进行试验。我们要记录下在疲劳试验机上从开始加载,一直到把试验件做坏期间,所施加的全部载荷历程。将这一试验载荷历程,按照之前我们介绍的与处理道路载荷完全相同的手段,处理成等效载荷幅值,从而获得n个样本yi。我们假设这n个样本也服从对数正态分布(可以通过检测对这一假设进行拟合优度检验),我们把这种分布称为(广义)强度分布。可以通过极大似然估计获得其样本均值
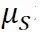
和方差
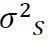
,以及强度分布中等效载荷幅值的中位数S0.50=exp(
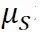
)。这里,我们用下脚标S(Strength,强度)标识与强度分布相关的量值。这样,我们就获得了双干涉模型的“右翼”。
可以明显感觉到,从技术上讲,“左翼”的获取比“右翼”的获取在技术上面临的困难和挑战要大的多。“右翼”的数据是否有积累,这里面本身没有技术上的壁垒,主要看一个企业是否作为。
2、车辆耐久性工程的核心“距离”——Φ
当建立了双干涉模型后,我们可以用它把很多问题解释的很清楚。比如说,为什么有的企业在更换了零部件供应商以后,会出现原本不存在的质量事故?如图2下方的图所示,一个可能的原因是新的零部件供应商提供的零部件,质量波动变大(反映在
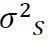
变大),强度也发生了降低(反映在
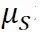
左移)。在车辆的其他设计和制造元素都没有发生改变的情况下,这样两种动向必然会引发事故增多。
因此,在我们花了大气力、大本钱获得了载荷分布和强度分布之后的任务,或者说,我们之所以要花大气力和大本钱来获得载荷分布和强度分布的目的在于:通过后续一系列的设计工作和试验工作来确保双干涉模型中的载荷分布与强度分布之间拉开合适的距离。
这个距离太近(像刚才谈到的更换比较糟糕的零部件供应商就使得这个距离太近了),将会引发失效率飙升;这个距离太远,像图2上方的那个图所示,将会引起过设计,这部车的轻量化、燃油经济性等方面的指标肯定好不到哪里去,或者说还有很大的潜力来把这些指标提升的更好。
所以,这个距离大了不行,小了不行,要刚刚好。这是一个度的把握!车辆耐久性工程的核心问题就落脚在把握好这个度,并通过之后的一系列设计工作和试验工作来确保和落实这个度!
如何来定量的描述这个度?我们习惯上使用如下的这个非常重要的量来定量刻画强度分布
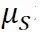
与载荷分布
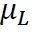
之间的距离
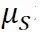
-
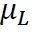
:
Φ=exp(
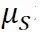
-
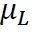
)= exp(
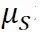
)/exp(
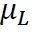
)= S0.50/L0.50
可以看到,如果
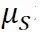
-
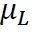
表示的这个距离越大,Φ就越大,而Φ实际表征的是S0.50/L0.50,也就是强度中位数相对于载荷中位数的倍数。我们习惯上称Φ为中心安全系数(CentralSafety Factor)。
图2 从双干涉模型感受“度”的把握及其重要性1
3 运用二阶法(Second-MomentMethod)来把握好这个度
不难证明,如果双干涉模型中左右两个分布都服从正态分布(根据之前的假设,对等效载荷幅值取对数后,载荷分布和强度分布都服从正态分布),那么有
其中,β为标准正态分布的上pF分位点。
这是一个至关重要的关系!因为这个关系说明:对于由两个正态分布构成的双干涉模型来说,两个分布的离散程度(
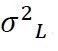
+
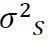
),与我们要把握的这个度lnΦ=
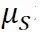
-
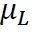
,通过标准正态分布N(0,1)与一个失效率pF关联了起来!
当我们没有办法改变载荷分布和强度分布的离散程度时,减小失效率pF(或者说提高可靠性),需要拉大强度与载荷之间的距离,反之亦然。这个距离,或者说我们要把握好的这个度,由于与失效率pF(或者说可靠性)通过标准正态分布N(0, 1)完美的关联起来,而得到了数量上的确定性关系!在这其中发挥重要作用的分位点β,我们习惯上称它为可靠性指数(Reliability Index)。
如何把握这个度?最终落脚在如何设定产品的可靠性指数(或者说失效率,或者说可靠性)上来。对于这个度最终确定,早已超出了耐久性工程的范畴,甚至早已远远脱离了纯技术的话题和范畴,它反映了企业对于产品质量与成本等诸多矛盾方面的妥协与平衡。
企业的终极目标,并不是不顾一切的向客户提供最耐久的产品,而是实现(长期)利润的最大化。这是一个经典的优化问题,其中企业的(长期)利润是目标函数,而耐久性,或者说我们要选取的这个指标pF,只不过是众多的约束条件之一。
图3是这样一种核心和艰难的决策结果的一个范例2。我们可以看到,企业在做这样一种决策时所要考虑的问题:同等情况下,安全性测试方面的相对花费比较低的话,企业可以承受将可靠性提高一些;同等情况下,如果失效引发的后果很严重(这里面涉及到将零部件依据其失效引发事故的严重程度进行分类的工作),企业愿意将可靠性提高一些。
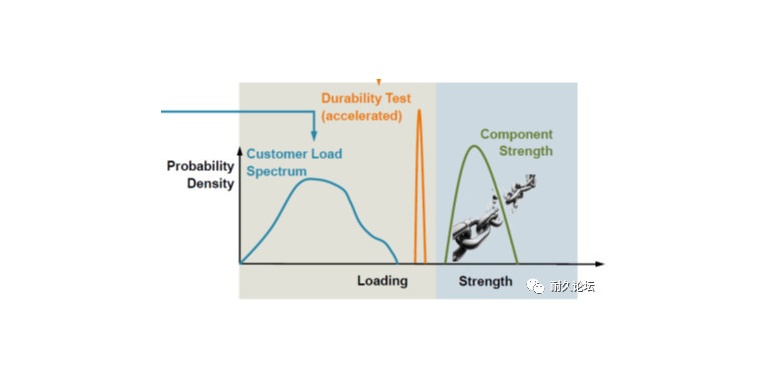
图3 目标可靠性指数β与一年参考期和最终极限状态有关2
无论多么纠结与痛苦,一旦企业明确给出了类似图3所示的企业标准或目标,我们如何把握耐久性工程中的这个度的问题,便迎刃而解了:
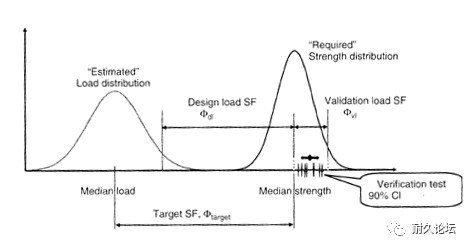
我们把这个与特定的β相关联的Φ,常常标注为ΦTarget,如图4所示,强调和提醒:这是我们在对于载荷离散性和产品质量波动无法干预的情况下,为了确保一定的产品可靠性,而需要在强度和载荷之间拉开的目标距离。
我们将看到,耐久性工程下游所有的设计工作和试验工作,都是为了确保这一目标的实现。或者说,ΦTarget的确定,为下游所有的设计工作和试验验证工作明确了目标。因此,双干涉模型的建立,对于耐久性工程具有全局性和战略性的指导意义,是一种顶层输入。而刚才我们谈过,相对于双干涉模型的右翼来说,左翼的载荷分布是更加难以获取和驾驭的分布,因此我们才不止一次的强调过,载荷分布对于(车辆)耐久性工程来说是一种具有全局性和战略性的顶层输入,因此我们也才在“耐久论坛”开立之初,撇开一系列的具体技术不谈,迫不及待的首先把西门子工业软件公司的CUCO技术加以介绍。
图4 双干涉模型及其对(车辆)耐久性工程下游全部设计和试验工作的全局性和战略性指导作用3
4 双干涉模型对于设计工作的指导
4.1 设计载荷Ldl的确定
在通过CUCO项目获取载荷分布后,一般选取覆盖90%到95%客户使用习惯的载荷作为设计载荷,不建议选择的更高,不建议超过95%的覆盖范围。
4.2 设计工作的任务
一切设计工作的任务,在于保证所设计的结构在设计载荷的作用下,其名义强度(Norminal Strength)满足ΦTarget所确定的强度中位数与载荷中位数之间的距离。这里面一个比较实用和具有可操作性的指标是Φdl=S0.50/Ldl,我们习惯上称之为局部安全系数(ParticalSafety Factor)。这一指标很明确的给出了强度中位数与设计载荷之间的距离,而通过这一距离我们很容易的做出比对和判断:与设计载荷对应的名义强度是不是太高了,需要修改设计降一降;或者是太低了,结构可以进一步优化。我们的中心安全系数ΦTarget已经千呼万唤始出来,一个很自然的思路是,建立Φdl与ΦTarget之间的关系,这个关系很简单:
上式中ΦTarget已经有了(这个是核心的、困难的和全局的),
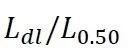
在选择设计载荷Ldl到底准备覆盖多少客户之时就已经确定了,因此,
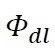
就确定了。
5、双干涉模型对于试验工作的指导
(车辆)耐久性工程中的试验有两大类:一类,称为特征试验(Characterizing Test),我们在1.2小节谈到的为了获取强度分布而开展的试验,就属于特征试验;另一类,称为验证试验(Verification Test)。双干涉模型对于全部验证试验都有重要的指导作用,事实上,双干涉模型与验证试验之间本来就存在着天然的逻辑关系。
我们在第3节通过二阶法给出了产品要达到一定的可靠性指标,强度和载荷之间要拉开的合理距离,那么验证试验实际上就是要通过试验确定,这个距离能不能保证?当作用在试验对象上的试验载荷Lvl达到甚至超过(我们马上讲为什么要超过)目标强度时,相关结构是否会出现异常。因此,双干涉模型对于验证试验载荷谱Lvl的指导意义在于:基于实际的(道路)载荷谱,按照既定的L0.50,将其向着试验载荷谱放大到
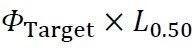
。这是在确定试验载荷谱Lvl时对于实际(道路)载荷谱L0.50的第一次放大。在此基础上,还要再放大一次。
为什么还要再放大呢?因为试验对象强度分布的固有离散性。我们选择一个试件进行验证试验,与选择多个试验件进行验证试验,自然会觉得试验次数越多,试验结果越可信。原因在于,试验对象强度分布的固有离散性,使得我们在选择较少的样本量进行试验时,很有可能因为“运气好”抽到几个相对来说质量比较高的试验件,从而“侥幸”通过验证试验,而使得试验结果失真。因此,为了使我们在选取少量、甚至只进行一次验证试验时,试验结果仍然能达到设定的置信度,我们需要把试验对象强度分布的固有离散性(这反映了试验对象的质量波动)考虑在内,再次加强试验载荷谱至原来的k倍。我们在《道路试验啊!这到底要开多远才是个头?——抽样分布与最小样本量的确定》一文中在介绍最小样本量的确定时谈到过区间估计的概念,在确定k值时就是针对试验对象的强度分布而进行的区间估计。因此可以知道,计划进行的试验次数越少、希望达到的试验结果置信度越高、试验对象的质量波动越大,我们需要把k值取得越大。故此,试验载荷为
6、车辆耐久性工程整体流程以及再次强调载荷分布的系统性和全局性作用
如图6所示,给出了车辆耐久性工程的整体流程。无论是实施CUCO项目还是借鉴已有的强化路面试验规范,我们需要基于相似车型进行道路载荷数据采集(图6左一)和数据处理(图6左二),建立耐久性工程的载荷边界;载荷、几何和材料三方面因素完整后,可以开展以多体动力学(MBS)、有限元(FEM)和疲劳寿命分析(FLP)为核心的三个层面的求解,构成系统级的耐久性仿真设计(图6左三);紧接着需要开展物理样机的验证试验,来确保产品的可靠性;在整车试验场验证方面,需要开展以试验场试验规范的制定为前提的整车强化路面试验,从而完成车辆耐久性工程的闭环。
从本篇文章我们可以清晰的看到:载荷分布是构成双干涉模型中最困难的环节,在构成了双干涉模型后,可以基于企业可靠性决策明确强度与载荷之间的安全裕度,从而指导下游的设计和台架试验。而载荷分布对于车辆试验场试验规范制定方面的指导作用在上一篇文章《客户相关的道路载荷大数据获取和道路载荷分布模型的构建》已经明确,即试验场验证规范是以CUCO项目获得的覆盖(比如说)95%客户群体的载荷边界为目标,通过CombiTrack技术制定的。
这样,我们应该比较明确的详细阐释和强调了:以CUCO项目为依托获取的与特定客户群体相关的道路载荷分布,对于车辆耐久性工程的全局性、战略性和极端重要性,是一个名副其实的顶层输入。一旦这个输入出现了统计偏性,将把这一偏性带入耐久性工程的全部下游工作。
图5 车辆耐久性工程的整体流程1
参考文献
1. 来源于西门子工业软件有限公司内部资料.
2.JCSS. Probabilistic model code. ISBN 978-3-309 386-79-6, 08 2001.
3. P.Johannesson, M. Speckert, Guide to load analysis for durability in vehicleengineering, 2014, Edition I, John Wiley & Sons, Ltd.
作者简介
李旭东,2003年毕业于大连理工大学机械工程学院,获工学学士学位;2008年毕业于北京大学力学系固体力学专业,获理学博士学位。2008年至2014年,就职于中国航空综合技术研究所,历任工程师、高级工程师;2015年至今,就职于西门子工业软件(北京)有限公司,任职耐久性应用工程师。长期专注于(金属)材料和结构耐久性和损伤容限分析方法研究。
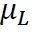 ,样本方差为
,样本方差为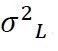 ,等效载荷幅值的中位数为L0.50=exp(
,等效载荷幅值的中位数为L0.50=exp(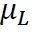 ),等等。借助CUCO,这些个数值目前我们都有了。
),等等。借助CUCO,这些个数值目前我们都有了。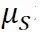 和方差
和方差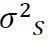 ,以及强度分布中等效载荷幅值的中位数S0.50=exp(
,以及强度分布中等效载荷幅值的中位数S0.50=exp(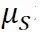 )。这里,我们用下脚标S(Strength,强度)标识与强度分布相关的量值。这样,我们就获得了双干涉模型的“右翼”。
)。这里,我们用下脚标S(Strength,强度)标识与强度分布相关的量值。这样,我们就获得了双干涉模型的“右翼”。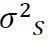 变大),强度也发生了降低(反映在
变大),强度也发生了降低(反映在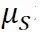 左移)。在车辆的其他设计和制造元素都没有发生改变的情况下,这样两种动向必然会引发事故增多。
左移)。在车辆的其他设计和制造元素都没有发生改变的情况下,这样两种动向必然会引发事故增多。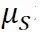 与载荷分布
与载荷分布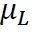 之间的距离
之间的距离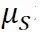 -
-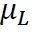 :
: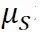 -
-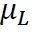 )= exp(
)= exp(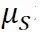 )/exp(
)/exp(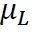 )= S0.50/L0.50
)= S0.50/L0.50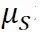 -
-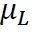 表示的这个距离越大,Φ就越大,而Φ实际表征的是S0.50/L0.50,也就是强度中位数相对于载荷中位数的倍数。我们习惯上称Φ为中心安全系数(CentralSafety Factor)。
表示的这个距离越大,Φ就越大,而Φ实际表征的是S0.50/L0.50,也就是强度中位数相对于载荷中位数的倍数。我们习惯上称Φ为中心安全系数(CentralSafety Factor)。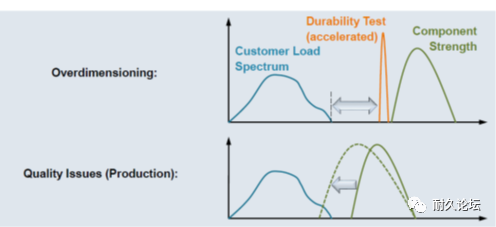
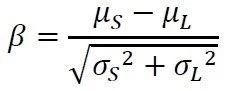
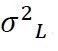 +
+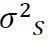 ),与我们要把握的这个度lnΦ=
),与我们要把握的这个度lnΦ=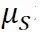 -
-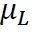 ,通过标准正态分布N(0,1)与一个失效率pF关联了起来!
,通过标准正态分布N(0,1)与一个失效率pF关联了起来!
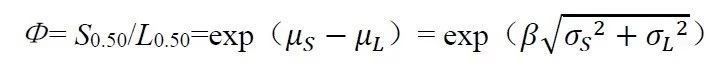
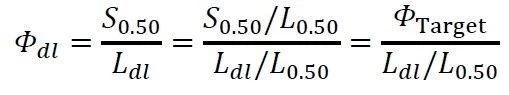
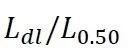 在选择设计载荷Ldl到底准备覆盖多少客户之时就已经确定了,因此,
在选择设计载荷Ldl到底准备覆盖多少客户之时就已经确定了,因此,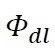 就确定了。
就确定了。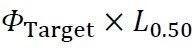 。这是在确定试验载荷谱Lvl时对于实际(道路)载荷谱L0.50的第一次放大。在此基础上,还要再放大一次。
。这是在确定试验载荷谱Lvl时对于实际(道路)载荷谱L0.50的第一次放大。在此基础上,还要再放大一次。






 广告
广告





























































