1 转向几何特性
当车辆低速转弯或准确说是车辆无侧向加速度时,四个车轮绕同一点作圆周运动,这点称为滚动瞬心,这是阿克曼转向的基本原理。根据阿克曼转向:内侧车轮和外侧车轮的转角关系如图1所示。
M为车轮的滚动瞬心;
j为前轮两主销轴线与地面交点间的距离;
δO,A为前轮外侧转向轮转角;
δi,A为前轮内侧转向轮转角;
△δA为阿克曼角
Rs为转弯半径
L为轴距
V为车辆质心
则j=bF-ro
△δ A =δ i,A -δ O,A
最小转弯直径:
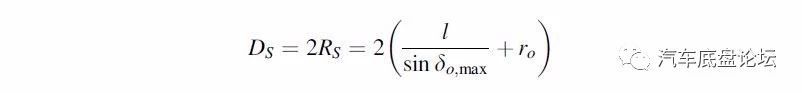
Ds:最小转弯直径;
Sinδo,max:最大外侧车轮转角
很显然,对于赛车而言,较小的轴距和较大的转角设计是设计希望的,但是转向轮的转角受悬架跳动空间和驱动轴角度限制,而较小的轴距设计又具有较差的动力学特性,也不适用于车身较长的车型设计。
对于给定的转弯半径,整车尺寸、轮距和轴距等参数对车轮转角设计影响最大,它们之间的关系需要在开发初期就进行确认。
这些参数的运动关系如图3所示:
如果车轮发生纯滚动(无轮胎侧滑),则车轮转角、轮距和轴距等参数间存在几何关系。在车辆概念开发阶段,这些参数可以从整车定义和法规等材料中获取。当车辆车轮的侧偏角较小时,滚动瞬心位于后轴的延长线上。随着车速增加,离心力变大、车轮轮胎的侧偏角也变大,滚动瞬心朝前轴移动,如图4所示。
转弯半径公式:
αF,i,αR,i,αF,o,αR,o为车轮的侧偏角;
β为车身偏航角;
M为阿克曼的滚动瞬心;
M’为实际的滚动瞬心;
Rtc,i为后轮内侧转弯半径,mm;
bV,R为后轮距,mm;
bF,bR为前后轮距,mm;
Rtc为最大转弯半径,mm;
a,e为距离尺寸,mm
如轴距为3000mm,前轮距为1490mm、后轮距为1540mm,最大转弯半径为7500mm,则外侧车轮转角需要设计为23.6°,后轮内侧转弯半径(最小,轮跳宽346mm)为5186mm。
最大转弯半径Rtc是一个理论概念,对于驾驶者来说转弯半径Rs的概念更普遍,一般乘用车的转弯直径<11m。
当车辆转弯时,车辆存在侧向加速,轮胎产生侧偏角并传递侧向力。滚动瞬心是每个轮胎弧线的垂线的交点,如图4所示。相对理想的阿克曼滚动瞬心,这个点相对前移。图4也说明,阿克曼转向时外侧车轮的侧偏角相对内侧车轮较小。
当车辆过弯速度大时,阿克曼转向限制了轮胎最大性能的发挥。外侧车轮承受较大的负载但无法提供更大的侧向力,因为轮胎侧偏角则呈现相反的设计即外侧车轮侧偏角较小。如果外侧车轮的转角大于内侧车轮,如图5所示。转向响应会更快,也会迫使外侧车轮的侧偏角更大,用这种方法可以增大前轴的转弯能力,但这种方法只使用于快速过弯情况。根据某车型试验,车轮转角为5°-10°时,更高的车轮转角可以使实际的阿克曼角曲线更接近理想的阿克曼角曲线,轮胎磨损和行驶阻力也相应减少,如图6所示。
如果转向轮的角度很小,内/外侧转向轮的角度可能相等(如平行转向,阿克曼角为零),与理想阿克曼转角的差称为阿克曼转角误差:
实际的阿克曼转角误差会生成一条类似理想阿克曼转角误差的曲线,从图6也可以看出,阿克曼转角误差是关于内侧车轮转角的函数。
如果转向轮转角较小,外侧车轮转角相对内侧车轮转角较大,便存在一个轮胎平行的过渡区,这时轮胎的过弯能力最强。实际曲线值接近理想曲线值得50%(如实际阿克曼转角差4°,理想阿克曼转角差为8°)。
实际阿克曼转角误差与理论阿克曼转角误差常用百分比来表达:
阿克曼百分比=△δ/△δA·100%
0%,平行转向;
100%,理想阿克曼转向。
阿克曼转角误差对于减少既定车辆转弯直径有好处,根据试验,1°的转角误差可以使整车的转弯直径减少约0.1mm,具体如下等式:
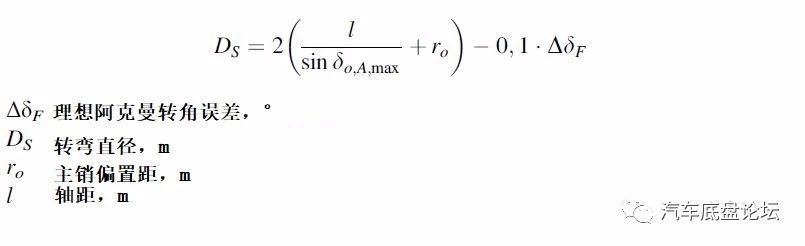
乘用车车轮最大转角一般为45°-50°,对应的转弯直径最小约为8m。
2 车轮定位参数
车轮的位置需要用一些参数来表达,如图8所示。
σ,主销内倾角,一般设计值5°-16°;
τ,主销后倾角,一般设计值1°-5°;
ro,主销偏置距,一般设计值-20mm-+80mm,图示为正值;
rσ,正视图主销偏距;
ra,轮心到主销轴线的力臂;
rt,k,主销拖距,一般设计值15mm-45mm;
nτ,侧视图主销偏距,一般设计值-5mm-+18mm,图示为正值;
εv,外倾角,一般设计值-2°-0°,图示为正值。
主销内倾角σ和主销后倾角τ影响车轮转向时外倾角εv的变化。主销轴线EG交于地面于点A,在正视图中,点A与点W的横向距离为主销偏置距ro,转弯时这两点的距离会变大。由于主销后倾角τ,主销轴线向后倾斜。从侧视图上看,轮心不一定位于主销轴线上,可能在前或后,形成侧视图主销偏距nτ。W与A在侧视图的距离为主销拖距rt,k。如果负的nτ值减小,则主销拖距rt,k也会减小,这造成转弯外倾角变化更大。
轮心到主销轴线的垂直力臂ra对作用到主销轴线的纵向力(如驱动力)响应十分重要,这个力臂也称为纵向力臂或合力力臂,因为所有的力都作用在车轮上然后通过轮心的轮毂轴承传递至主销轴线上。
图7展示了车轮定位参数的设计目标范围,上述的参数可以用来分析力对轮胎的影响,如图9所示。
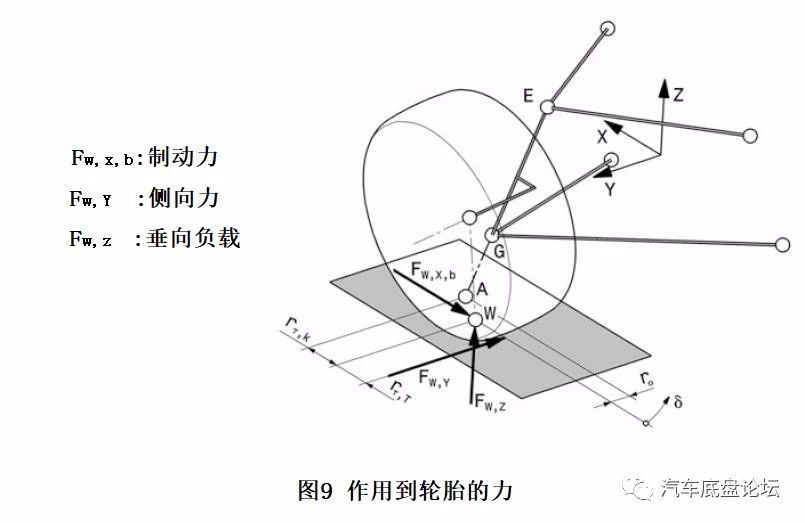
如果车轮受到X向的制动力,则制动力和主销偏置距会生成一个绕Z轴旋转的力矩。
MA,Z,b=Fw,x,b·ro
MA,Z,b,制动力绕主销轴线交点A产生的力矩,这个力矩绕Z轴旋转而不是主销轴线,Nm;
Fw,x,b,轮胎制动力,N;
ro,主销偏置距,m;
关于主销轴线旋转的力矩分量是:
MA,b=Fw,x,b·ro·cosσ·cosτ
MA,b,作用在主销轴线上的旋转力矩,Nm;
很明显,主销偏置距越大,制动力产生的绕主销轴线的力矩也越大,主销偏置距应设计的尽量偏小些,这样两轮在不同制动摩擦条件下对转向的影响小些。乘用车常常采用负的主销偏置距设计,制动力左/右不等时可以保证车辆的直行行驶。对于双横臂悬架来讲,实现负的主销偏置距设计很困难,会导致制动盘或卡钳无布置空间。可以将A型横臂分解成两个横臂,这样就满足布置和负主销偏置距的设计。
侧向力的作用力臂为主销拖距rt,k和轮胎拖距rt,T之和。
由于主销轴线并不垂直于地面,当车轮转向时,轮心与地面间的距离发生变化。也就是说车轮负载影响着转向力矩,也包含驾驶者的方向盘力矩。这种情况可以用车轮负载力臂q表达,q的表达式:
q=ro·tanτ+rt,k·tanσ
q是车轮负载力臂
如果主销轴线垂直或力作用到主销轴线上,车轮负载不会产生力矩作用。
当车轮负载可以使车辆转向轮产生回正的作用,车轮负载力臂为正值。车轮负载力臂也可以看成一个前悬高度/方向盘角度的导数
如果车轮负载力臂为正,打方向盘会使车头抬升。
重力回正力矩计算公式:
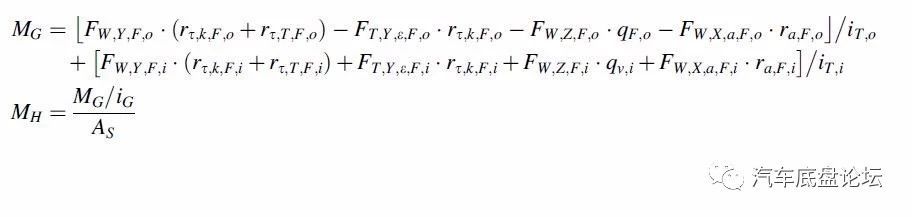
MG:作用在转向器上的力矩,Nm
rτ,k:主销拖距,mm
rτ,T:轮胎拖距,mm
Fw,Y:侧偏侧向力,N
Fw,Y,ε:外倾侧向力,N
Fw,Z:车轮负载,N
Fw,X,a:驱动力,N
ra:纵向力臂,mm
iT:杆系传动比
MH:方向盘力矩,Nm
iG:转向器传动比
δG:摇臂的角度
As:转向放大因子
车轮负载力臂很小,所以车轮负载波动对转向影响较小。重力回正只有在低速转向或原地转向时较为明显,当车辆高速转向时,侧向力产生的回正力矩占主导作用。
当车辆高速过弯时,方向盘的角度一般都很小,前悬的阿克曼转角误差是可以忽略不计的。无论是阿克曼转向还是平行转向,轮胎侧偏角会使车轮的滚动瞬心前移。轮胎侧偏产生的侧向力FW,Y,F主要产生方向盘阻力,而重力回正的影响则十分小。外倾侧向力作用在轮心处,而轮胎侧偏产生的侧向力作用在轮胎拖距处。且外侧轮胎所受的侧向力要大于内侧轮胎,因为转向时轮荷转移到外侧轮胎。如果车辆是前驱型式,则驱动力矩会通过纵向力臂ra作用到主销轴线上,影响转向操纵,如图10所示。
对于大多数悬架来说,转向时外侧车轮主销拖距变大、内侧车轮主销拖距变小。轮胎拖距随着侧向加速度增大而减小,这也使外侧轮胎侧向力的影响减小,侧向力也会造成方向盘角度的增加。但由于外轮转向连杆的传动比比内轮增大的多,则外侧车轮的转向力矩相对内轮的贡献会减小,因此这个现象也不明显。
主销后倾角和内倾角也会造成转向时外倾角的变化。如果主销后倾角为0°、外倾角为0°,转向轮转动90°会使外倾角发生变化且变化角度等于主销内倾角,如图11所示。当转向时,轮心UF绕主销轴线EG旋转。在侧视图上,运动轨迹像是椭圆;当车轮转角为零时,椭圆的切线与水平线的角度为主销后倾角,曲线的曲率半径ρ由瞬心P决定。P的位置是车轮中心垂线与主销轴线的交点,几何关系如下:
ρ=ro/(tanσ·cosτ)
因此外倾角曲率也与主销内倾角成一定比例关系,当转向时,正角度倾斜的主销轴线使外倾角朝正值变化。外倾角的变化率取决于主销后倾角和主销内倾角。
图12比较了不同转向几何设计的影响

a设计采用较小的主销后倾角和内倾角,但主销偏置距较大;b设计具有较大的主销内倾角和较小的主销后倾角,主销偏置距为零;c设计和d设计有较大的主销后倾角和内倾角,但是主销偏置距较小。对比分析结果:
1)c和d外倾角曲线在转角为零时的斜率比其他曲线小的多,a和b外倾角曲线斜率约是c和d的3倍,这与主销后倾角大小有关;
2)具有较大主销内倾角的曲线b相对于a弯曲程度更大,但转向(外轮)角度为-30°时,外倾角为变为正值;
3)一般来讲,外轮的外倾角变化应在负值区域,而内轮外倾角变化因为正值或至少为一个增大的负值。c和d的曲线是设计所希望的,b曲线设计存在缺陷。
4)所有的曲线内侧车轮的主销后倾角增大,外侧车轮减小至负值区域;
5)所有曲线在方向盘中间位置时都受重力回正的影响,因为此时的车轮负载力臂均为正值。对于内侧车轮(正的转角区),这个结论是正确的;对于外侧车轮,只有特定的转角区域是正确的。曲线d是设计上所希望的,而曲线a则需要较大的-30°转角;
6)如果主销偏置距不为零,当车辆转弯时,轮胎接地印记中心会横向移动。如果前悬的主销偏置距相等,则转向时车头会横向移动。这会增大轮胎原地转向时的变形和转向力矩。曲线a最接近理想曲线即内外侧车轮主销后倾角相同,曲线c和d需要较大的原地转向力矩。
7)曲线b和d的主销偏置距为零,但是它们的轮胎接地印记中心在转向时仍然移动,因为主销后倾角的存在。如果想让轮胎原地转向,则主销后倾角和主销偏置距都应该为零。
3 转向传动比
当车轮的最大转角确定后,方向盘与车轮间的转向传动比就可以定义了。为了保证安全,轮胎与方向盘之间必须存在机械传动结构。转向运动通过转向器由方向盘传递至轮胎,转向器存在传动比iG来减小方向盘手力,轮胎与转向器之间的转向杆系也存在一个传动比,并随着方向盘角度而变化。
角传动比is等于方向盘角度δH与左/右车轮平均转角的比值δm
is=δH/δm
在所有的齿条行程内,转向传动比有时不是固定的。上面的等式只适用于特定的转向区间。
车辆高速行驶时转向响应应慢一些,在齿条行程内传动比有最小的限值,乘用车一般≥14,转向传动比的最大限值取决于原地转向的手力和是否存在助力,但很少有车辆的传动比最大值超过20;角传动比是杆系传动比和转向系传动比的总和,且在计算杆系传动比时内/外侧车轮转角都要考虑。如果转向杆系尺寸是已知的,则杆系传动比为有效节臂和摇臂的关系(循环球转向器)或有效节臂与小齿轮输入轴半径的比值(齿轮齿条转向器)。
由于零件存在刚性和间隙,所以实际的传动比与理论计算是有出入的。车轮在转动前方向盘存在空行程。图13展示了齿轮齿条转向器车型的测试。
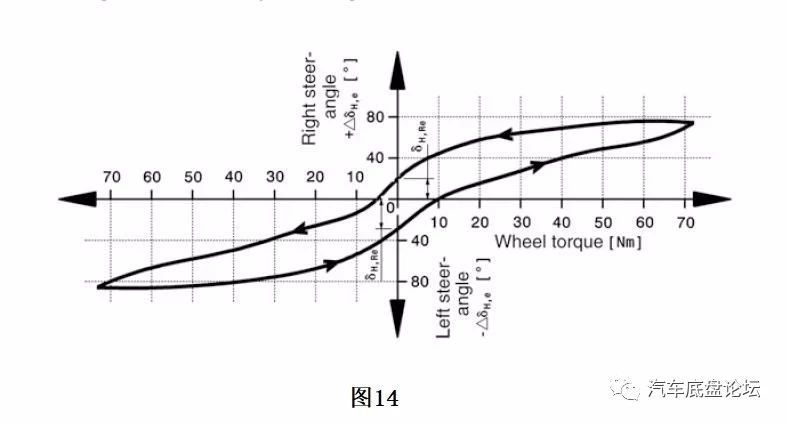
试验方法:
1)车辆固定,然后在方向盘上施加一定力矩;
2)方向盘角度△δH,e随车轮所受力矩增大而增大;
3)在车轮承受力矩前方向盘存在空行程△δH,Re。
动力学转向传动比是考虑转向零件刚度和间隙的传动比:idyn=is+△δH,e/△δH
△δH,e,在车轮承受力矩前方向盘存在空行程△δH,Re
△δH,当车轮开始承受扭矩时方向盘转动的角度
换而言之,转向系统刚度使驾驶者感觉转向传动比变大,方向盘必须转动比理论计算较大的角度才能实现既定的车轮转角。如果转向力矩增加(如越野路行驶),方向盘的空行程也会增加。如果转向杆系的球铰阻尼较小,则在行程内转向系统的实际传动比会产生无规律的波动。因为前驱车辆位于前壁板和发动机间的狭小间隙,转向系统刚度较小,前驱车辆会差于后驱车辆。从方向盘中间位置至行程极限,前驱车辆的转向传动比会减小17%-30%,后驱车辆的转向传动比只减少5%-15%。
解决这个问题可以采用变转向传动比的方案,如图15所示。

4 转向杆系
无论是齿轮齿条转向器还是循环球转向器,都是将转向运动传递至转向节臂。最好的办法就是采用连杆连接传递运动,不仅可以满足转向运动还可以满足车轮跳动运动,图16展示了一些可能的杆系布置方案。
如图17中,转向杆系的布置角度对车辆安全有十分重要的影响。
βU,βT为传动角度
u为横拉杆长度
r为转向节臂长
e为有效节臂长
f为有效摇臂长
cδ为车轮绕主销轴线的旋转刚度
Cst为转向横拉杆刚度
a为横拉杆与转向节臂连线上的重合长度
如果传动角度βU、βT等于零,则杆系是不稳定的。虽然齿轮齿条转向器没有摇臂且回转中心D是一个较远的点,但这里仍然有一个转向力臂。被动臂的旋转角度βU可能变小到最小限值以下,这样转向杆系便没有限制。在满足行程和弹性的情况下,需要定义最小运动角度。传动角度应大于25°,转向杆系传动比为:
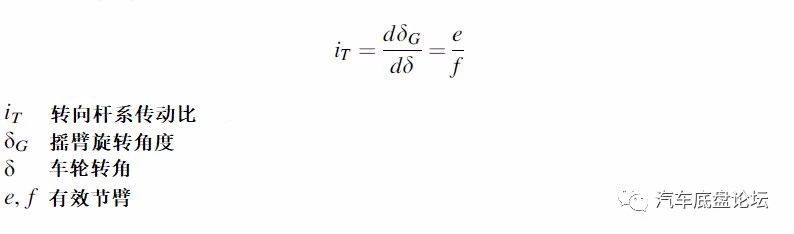
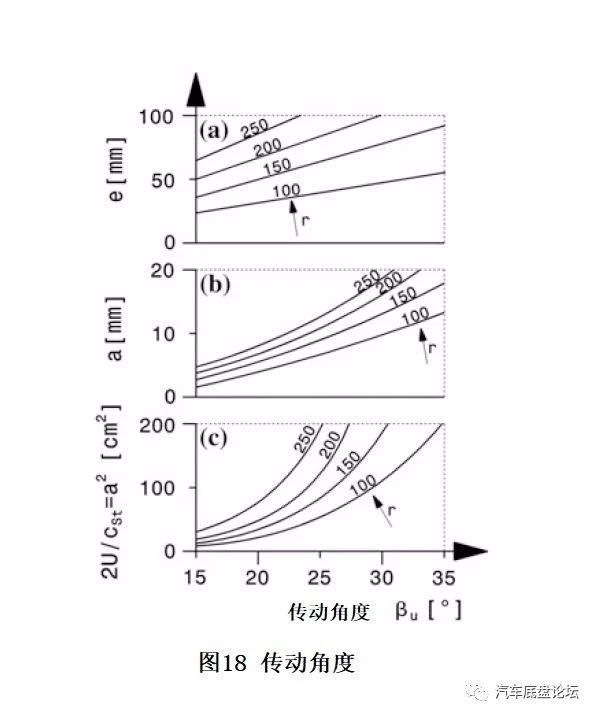
转向节臂长r是评估转向安全的一个重要参数,图18展示了一些关于传动角度βU和一些变量的对比曲线(横拉杆长u=300mm)。图c表示当转向杆系到极限时的做功能耗,说明减少转向节臂引起转向传动角度变大,并不能降低做功能耗。对于乘用车来说,长转向节臂-传动角度≥20°、短转向节臂-传动角度≥30°;
图a,有效节臂长度随着传动角度和转向节臂长度的增大而增大;
图b,转向节臂与横拉杆连线上的重合尺寸是从转向限制点开始测量的尺寸,较小的a值增加转向限制的风险。从这个角度讲,较大的转向节臂和传动角度是设计上所希望的;
图c,横拉杆是杆系中唯一的弹性杆cδ=cste²,则在横拉杆弯曲前的做功消耗U=csta²/2
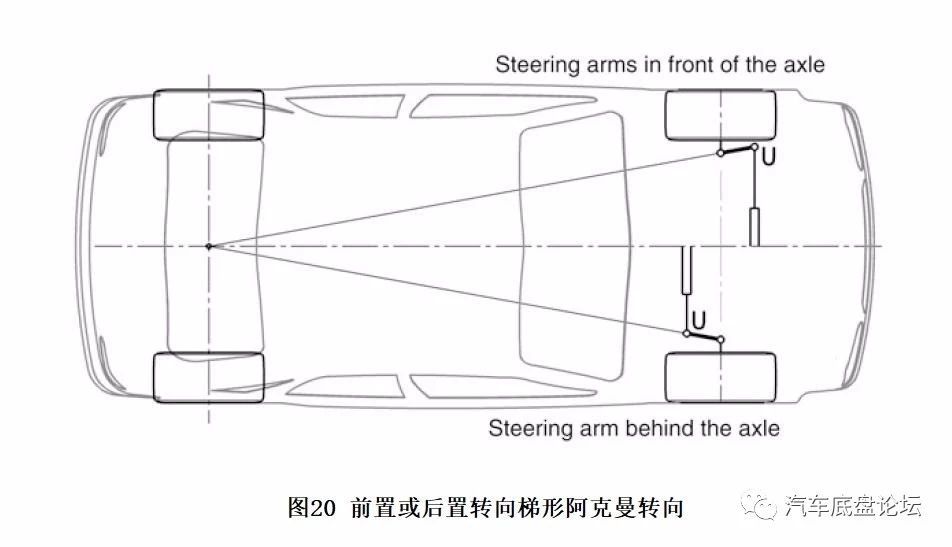
齿轮齿条转向的传动角度需要详细校核,小齿轮轴与齿条轴线的位置关系取决于转向梯形的布置。为了保证方向盘与车轮的转动方向相同:前置转向梯形,小齿轮轴位于齿条后方;对于后置转向梯形,小齿轮轴位于齿条前方。
转向节臂可能布置在轮心前方或后方,但是无论哪种布置,转向节臂都要与车辆纵向中性面呈一定倾斜角度,以实现阿克曼转向。
然而实际设计中很难实现理想阿克曼转向,当车辆转向时,点T和U的运动趋势是不同的。点T的运动轨迹是一条直线,点U的运动轨迹是绕主销轴线EG的空间圆,如图21所示。
当设计转向几何时,采用如下方法确定转向杆系硬点,尽可能实现理想的转向设计。
下面是关于前轴转向几何的几种基本布置方案,小齿轮轴布置在齿条前方或后方,相应的转向节臂布置在轮心后或前方,如图22、23、24所示。
前轮跳动时不应该引起前束的变法即无转向运动,关键控制因素是点U和T的位置。在进行运动学分析前应先定义转向节臂长度,如图25所示。转向节臂长度一般在100mm左右。
转向梯形前置,设计转向节臂和横拉杆时还要考虑车轮空间,当车轮处于最大转角时,转向横拉杆或节臂不应与车轮干涉。同时考虑装配误差和杆系弹性,设计上要留有足够的设计间隙,如图26所示。
当点U的位置确定后,横拉杆内球铰点T便可以确定了,这时瞬心就有用了。双横臂悬架如图27、28、29所示。点T确定后,转向器的位置也便确定了。
1)连线EG、GD交于点P1;
2)连接EU、CD交于点P3;
3)连接UP1取角α,以等角做直线P1P2,延长EG交于P1P2于点P2;
4)连接P2C交于P1U于点T
如果转向器位置需要布置较高,横拉杆也会布置在上横臂之上,如图28;
如果横臂是平行的,那么转向横拉杆也应该与它们平行,如图29;
麦弗逊悬架如图30、31确定T点位置。
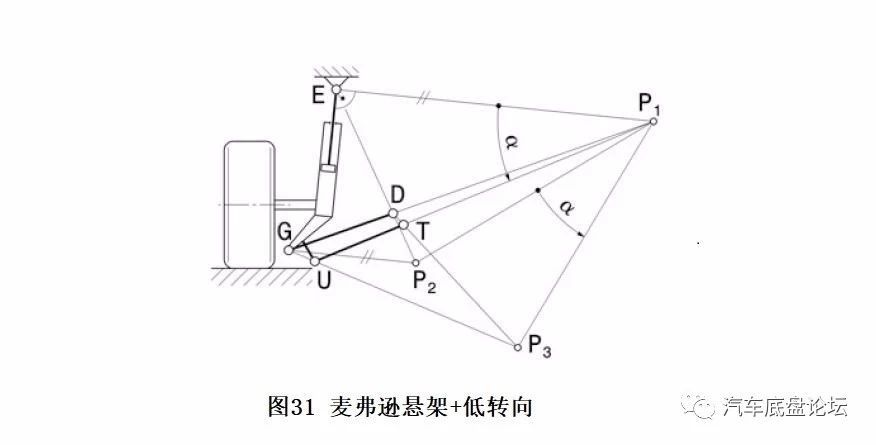
如图所示点U的位置越高,点T的位置约靠近车辆中心。当转向齿条行程较大时可能引起布置问题。
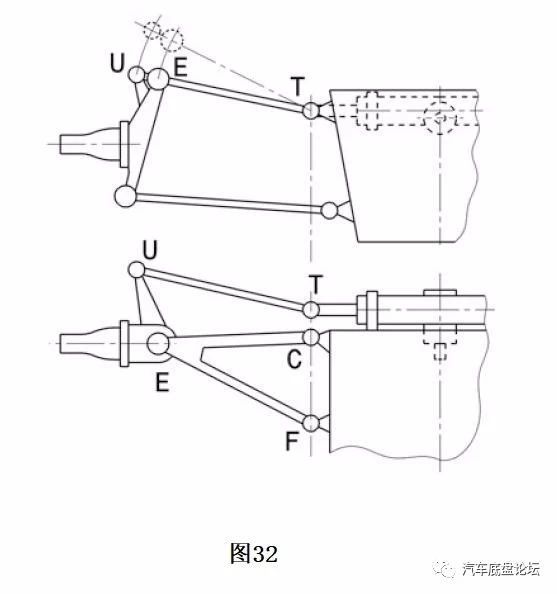
对于双横臂悬架,为了避免跳动转向,点T应位于摆臂旋转轴线CF的延长线上(俯视图),如图32所示。

设计上很难实现理想的转向几何设计,往往采用仿真软件进行综合分析,在现有条件下寻找尽可能接近理想的布置方案。
附转向齿条位置和横拉杆长短对跳动转向影响:
——————完——————
微信号:VehicleChassisForum

 则j=bF-ro
则j=bF-ro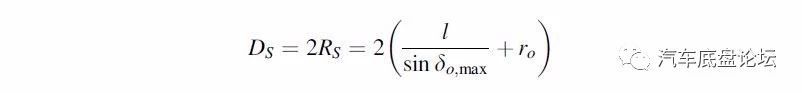 Ds:最小转弯直径;
Ds:最小转弯直径;


 如轴距为3000mm,前轮距为1490mm、后轮距为1540mm,最大转弯半径为7500mm,则外侧车轮转角需要设计为23.6°,后轮内侧转弯半径(最小,轮跳宽346mm)为5186mm。
如轴距为3000mm,前轮距为1490mm、后轮距为1540mm,最大转弯半径为7500mm,则外侧车轮转角需要设计为23.6°,后轮内侧转弯半径(最小,轮跳宽346mm)为5186mm。



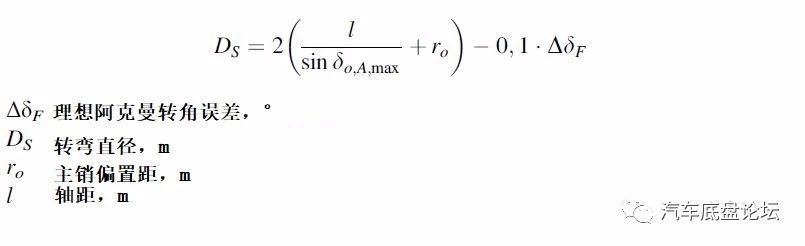 乘用车车轮最大转角一般为45°-50°,对应的转弯直径最小约为8m。
乘用车车轮最大转角一般为45°-50°,对应的转弯直径最小约为8m。
 如果车轮受到X向的制动力,则制动力和主销偏置距会生成一个绕Z轴旋转的力矩。
如果车轮受到X向的制动力,则制动力和主销偏置距会生成一个绕Z轴旋转的力矩。
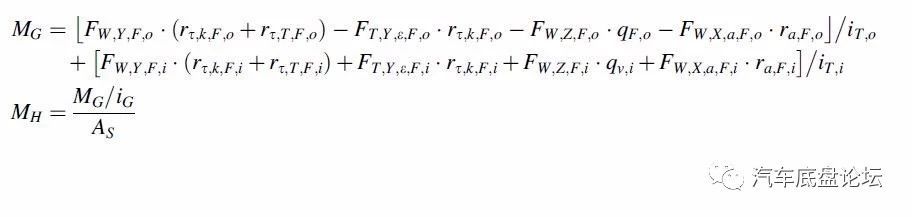 MG:作用在转向器上的力矩,Nm
MG:作用在转向器上的力矩,Nm


 a设计采用较小的主销后倾角和内倾角,但主销偏置距较大;b设计具有较大的主销内倾角和较小的主销后倾角,主销偏置距为零;c设计和d设计有较大的主销后倾角和内倾角,但是主销偏置距较小。对比分析结果:
a设计采用较小的主销后倾角和内倾角,但主销偏置距较大;b设计具有较大的主销内倾角和较小的主销后倾角,主销偏置距为零;c设计和d设计有较大的主销后倾角和内倾角,但是主销偏置距较小。对比分析结果: 试验方法:
试验方法: 4 转向杆系
4 转向杆系

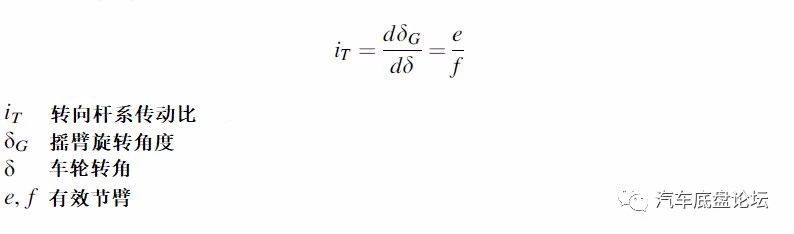 转向节臂长r是评估转向安全的一个重要参数,图18展示了一些关于传动角度βU和一些变量的对比曲线(横拉杆长u=300mm)。图c表示当转向杆系到极限时的做功能耗,说明减少转向节臂引起转向传动角度变大,并不能降低做功能耗。对于乘用车来说,长转向节臂-传动角度≥20°、短转向节臂-传动角度≥30°;
转向节臂长r是评估转向安全的一个重要参数,图18展示了一些关于传动角度βU和一些变量的对比曲线(横拉杆长u=300mm)。图c表示当转向杆系到极限时的做功能耗,说明减少转向节臂引起转向传动角度变大,并不能降低做功能耗。对于乘用车来说,长转向节臂-传动角度≥20°、短转向节臂-传动角度≥30°;


 当设计转向几何时,采用如下方法确定转向杆系硬点,尽可能实现理想的转向设计。
当设计转向几何时,采用如下方法确定转向杆系硬点,尽可能实现理想的转向设计。








 如图所示点U的位置越高,点T的位置约靠近车辆中心。当转向齿条行程较大时可能引起布置问题。
如图所示点U的位置越高,点T的位置约靠近车辆中心。当转向齿条行程较大时可能引起布置问题。 设计上很难实现理想的转向几何设计,往往采用仿真软件进行综合分析,在现有条件下寻找尽可能接近理想的布置方案。
设计上很难实现理想的转向几何设计,往往采用仿真软件进行综合分析,在现有条件下寻找尽可能接近理想的布置方案。





 广告
广告





























































