广告
电动汽车高速齿轮的振动噪声分析方法
2019-06-03 23:21:02· 来源：EDC电驱未来
电动汽车电机比汽油发动机噪声低，更重要的是，为了有更高的功率密度，此类电机转速目前正从8 000 r/min向12 000～16 000 r/min的高速方向发展，其减变速器齿轮
电动汽车电机比汽油发动机噪声低，更重要的是，为了有更高的功率密度，此类电机转速目前正从8 000 r/min向12 000～16 000 r/min的高速方向发展，其减变速器齿轮的振动噪声就成为一个发展瓶颈[1]。这不仅需要提高齿轮制造精度到5级或更高，还需要选择合理的设计参数和修形方法，以优化传动性能，减小振动噪声的激励源——传动误差[2]37。
齿轮的振动噪声研究属于齿轮动力学的范畴。相关理论研究和利用商业化齿轮模拟分析软件的动态模拟分析案例的文献较多。齿轮的振动噪声研究最初以冲击理论为基础，逐渐发展到以振动理论为基础进行分析，通过建立一系列齿轮振动理论模型[3]，对齿轮进行振动分析，取得了丰硕的成果；并且随着计算机的发展，出现了不少商业软件，如Romax、Mas⁃ter等，便于企业对具体产品进行优化设计。
但在实际应用中，理论研究和软件模拟两者通常是相对独立的，理论研究缺乏对直观的设计指导，模拟分析又局限于具体齿轮参数，一般的齿轮设计者无所适从。本文试图理论联系实际，探讨高速齿轮传动误差的优化和振动噪声预测的一般方法。
高速齿轮一般采用较大螺旋角的斜齿轮，以便提高齿轮重合度和降低传动误差。传动误差包括制造时的齿廓、齿距误差和轮齿啮合变形的变化量。文献[4]53-55已经就齿廓啮合变形和传动误差的计算提出了便捷的计算方法，需要就齿廓修形和传动误差的优化进一步探讨。
振动噪声除了传动误差的激励外，还与系统的动态响应有关[5]，直接建模分析较为复杂，一般通过齿轮模拟分析软件进行。本文中则通过简化的动态模型分析，提出优化的途径。
1 齿廓修形与传动误差优化
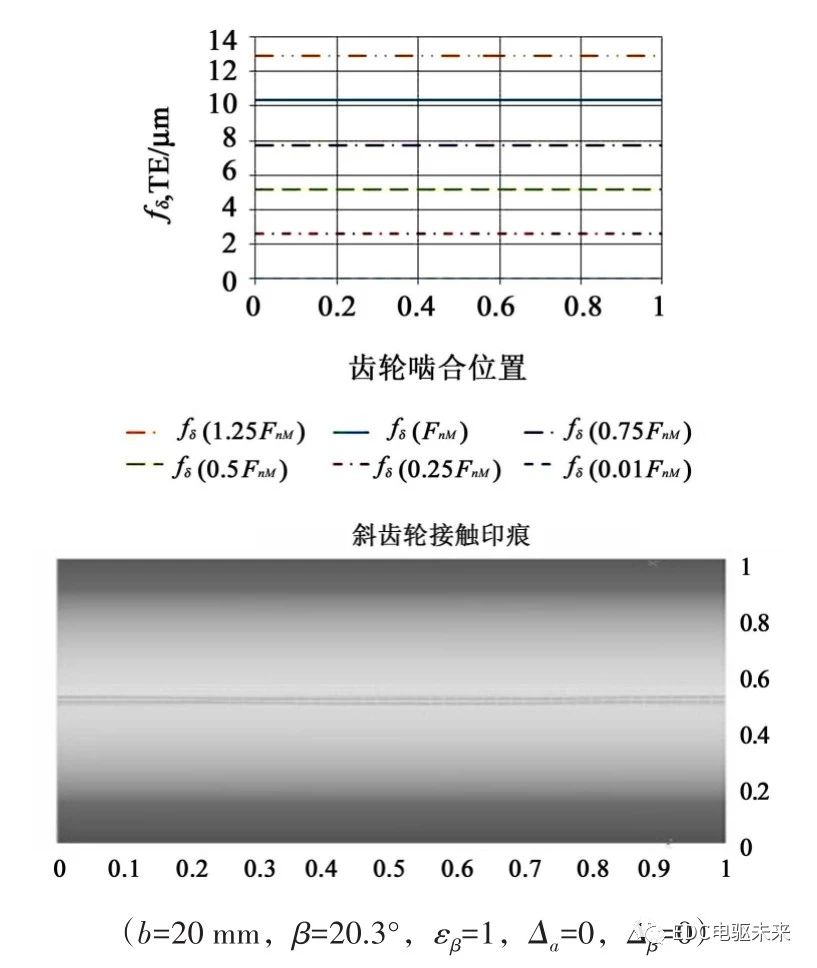
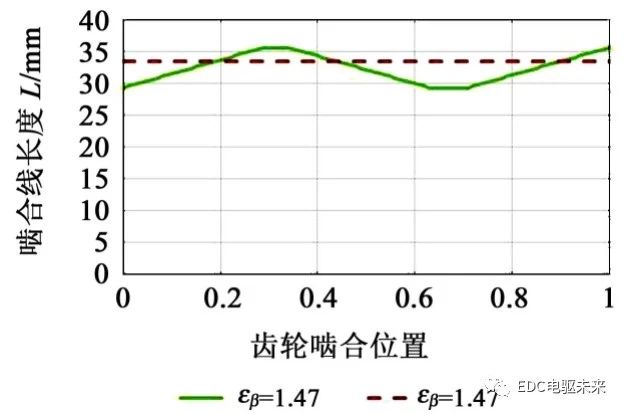
斜齿轮的优点是接触线的倾斜，使得轮齿的接触不再受到单双齿对啮合刚度差的影响，变形均匀性大幅提高。但由于接触线总长的变化，仍然有刚度变化引起的变形不均匀和传动误差。文献[4]55说明了在轴向重合度（εβ=1，2，…）为整数时，接触线总长不变，这使得传动误差很小。图1～图3是本文编程计算的接触线总长、不同载荷传动误差和接触印痕。计算的齿轮参数为z1=29、z2=37、mn=2.2、ha*=1、c*=0.25、αn=17.5°。下图中Δa为齿顶修形量，Δβ为齿宽修形量。
图1 不同修形条件下变形与传动误差、接触印痕
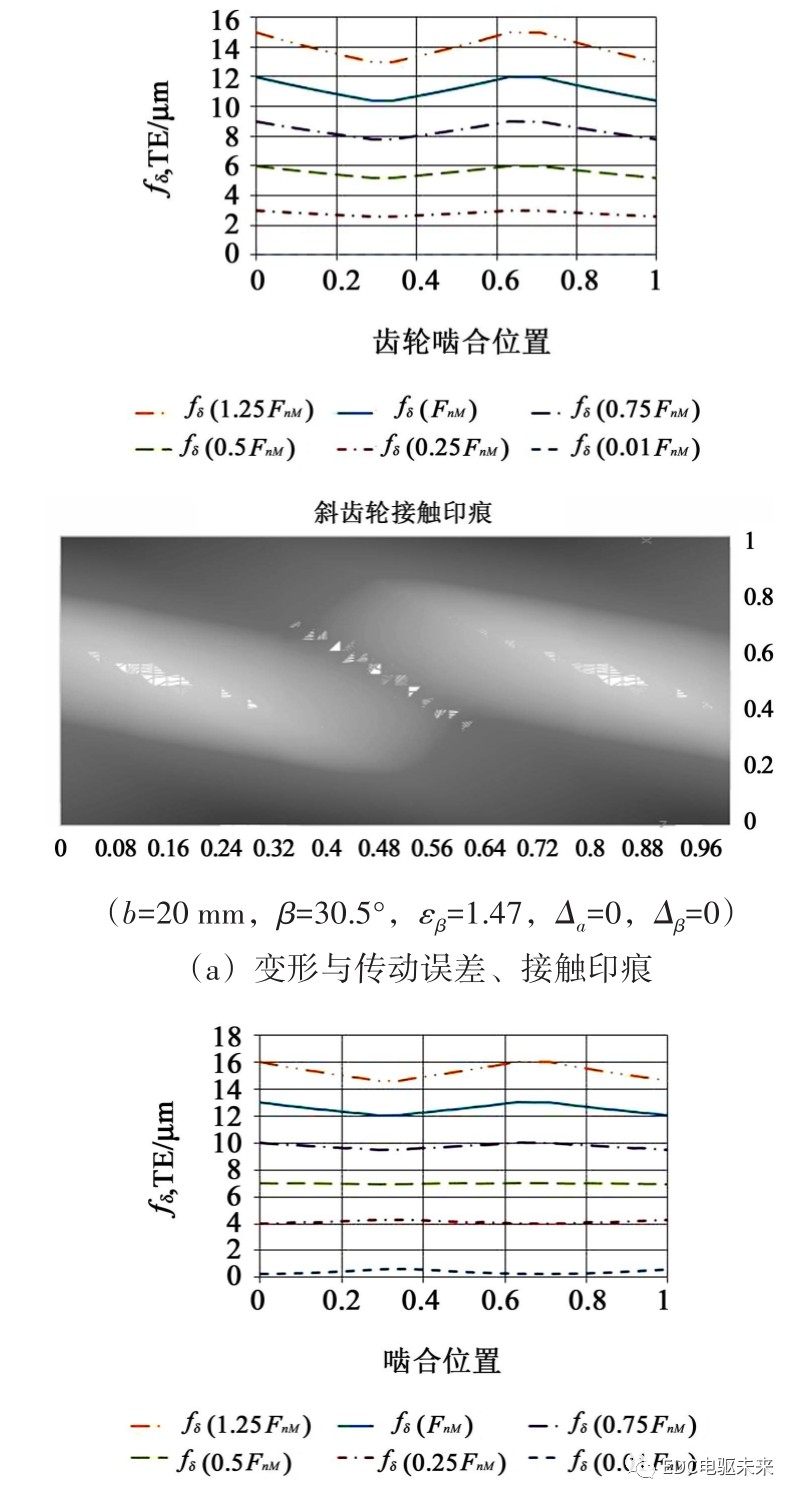
图1中，εβ=1.47，接触线总长变化较大，造成变形不均匀和传动误差TE较大。图1（a）未修形，TEmax=1.623 μm，图 1（b）进行齿廓修形（Δa=3 μm）和螺旋线鼓形修形（Δβ=2 μm），则TEmax=0.968 μm，有所减小，但无法消除；接触区也有所改善。
图2中，εβ=1，接触线总长恒定，TEmax=0.003 μm，接触区非常好。因此，εβ取整数有很好地减小传动误差的效果。当然，可以进行少量螺旋线修形，可以减小错位和齿廓偏差的影响。但因高速传动的载荷和变形一般较小，对修形参数比较敏感，过大的修形会造成接触区减小，反而增大传动误差。
图2 变形与传动误差、接触印痕
图3 不同重合度下接触线长度的变化
传递误差TE（t）是以齿频ω0为基频的周期性函数，可以展开为傅里叶级数
各阶幅值ui即构成为传动误差的频谱，见图4。
图4 传动误差的频谱
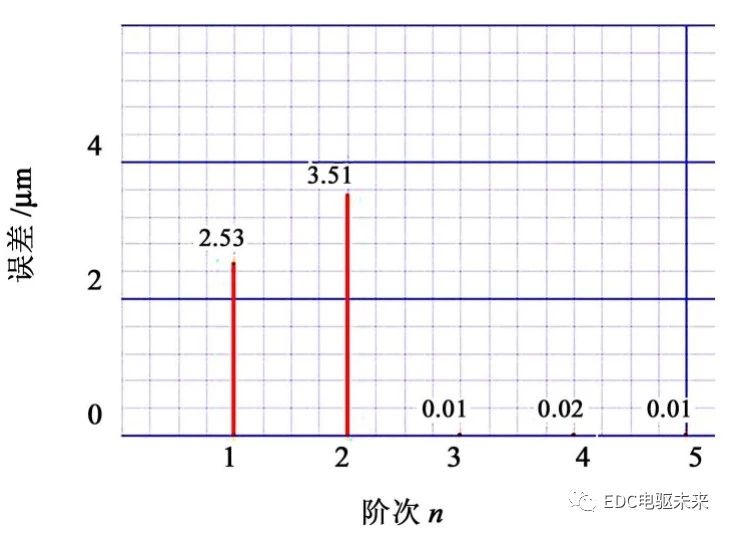
传动误差频谱是评价齿轮振动激励作用的基本参数。一般前3～5阶的幅值相对较大，是重点考查项。
2 传动误差激励下的系统振动理论
在传动误差激励下，齿轮系统构成一个多自由度振动系统[2]156。
将齿轮转动惯量和扭转刚性等效到基圆上的线性坐标，则有齿轮等效扭转质量me1、 me2，齿轮质量mo1、mo2，输入轴、输出轴的弹性扭转等效刚度ke1、 ke2、弯曲与轴承变形等效刚度kx1、kx2，两齿轮啮合刚度kT，其振动模型见图5。
图5 齿轮多自由振动数学模型
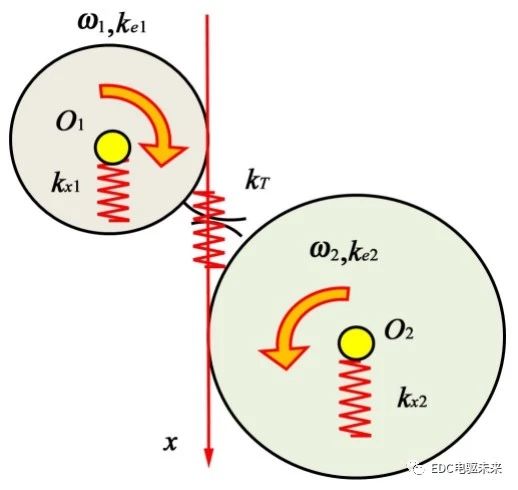
不计齿轮轴向振动，系统的振动微分方程为[2]163-166
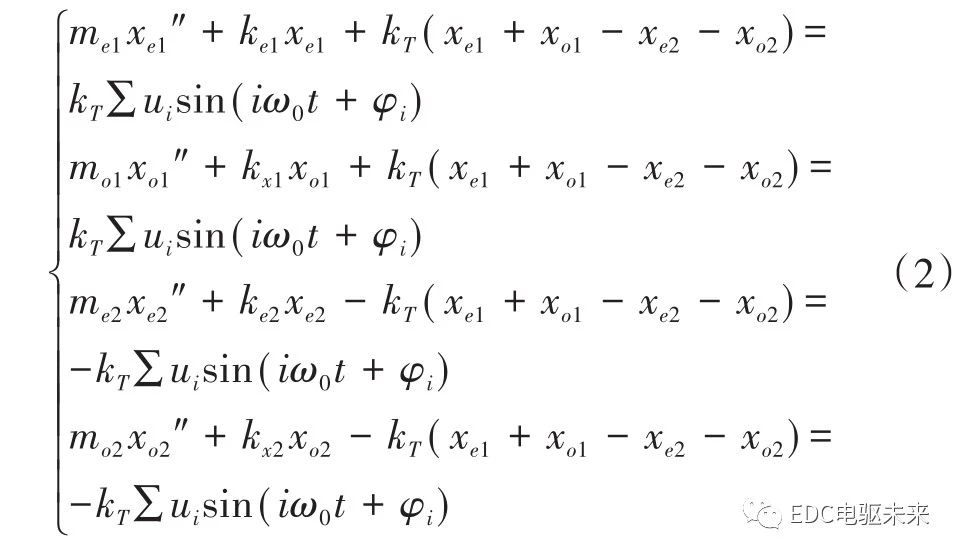
系统的自由振动会因阻尼作用而很快消失，所以只考虑TE（t）激励下的系统的稳态强迫振动。
因为强迫振动的频率与各阶激振频率iω0和初相位φi相同。因此按照激振阶次i分别处理公式（2）。
对不同阶次i的激励，其强迫振动可表示为
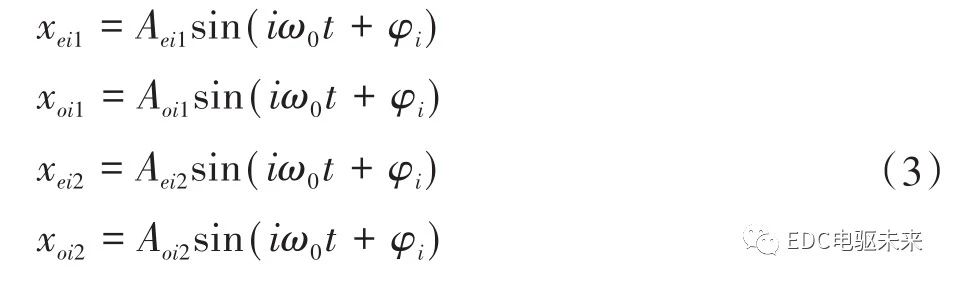
则，
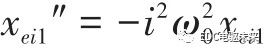
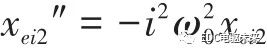
将式（2）整理后得到
其中，
简化后的等效刚度ki1、ki2和位移xi1、xi2等均为与阶次i有关的常数。而齿轮啮合刚度kT本来应该是周期性函数，这里取其均值，其变化的影响包含在TE（t）的变形部分。对应TE（t）的不同阶次的激励，这就简化为一个无阻尼双质量振动系统，数学模型见图6。
图6 齿轮扭转振动理论模型
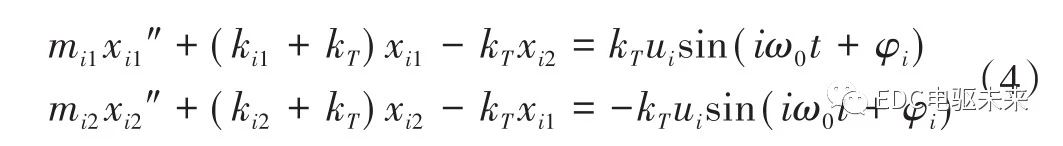
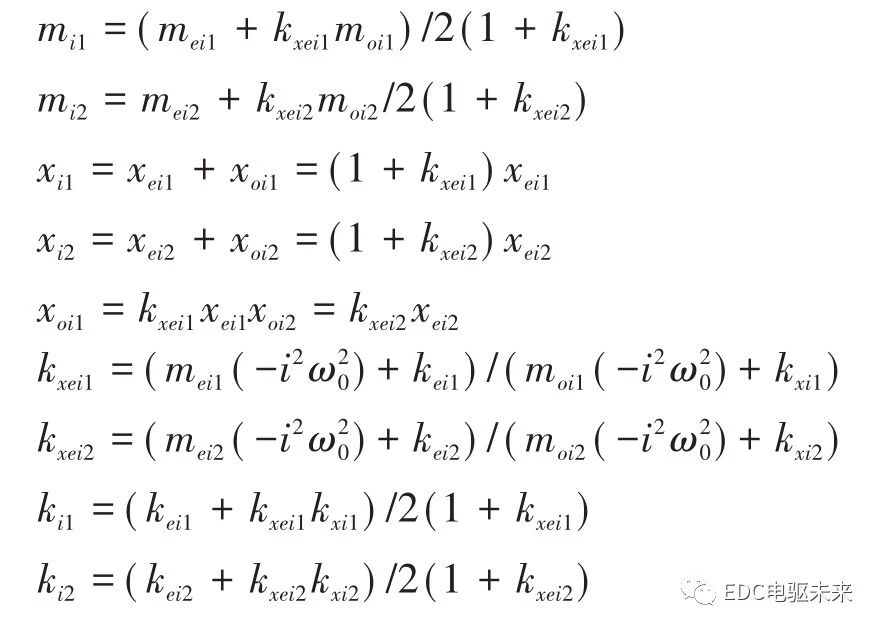
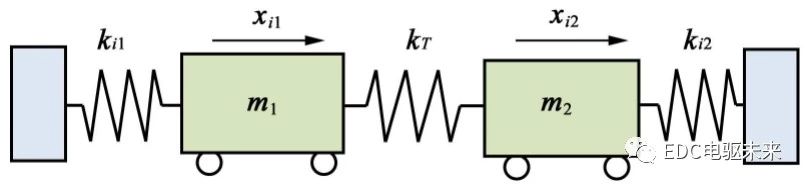
双质量振动系统有2个固有频率，分别为
其中，
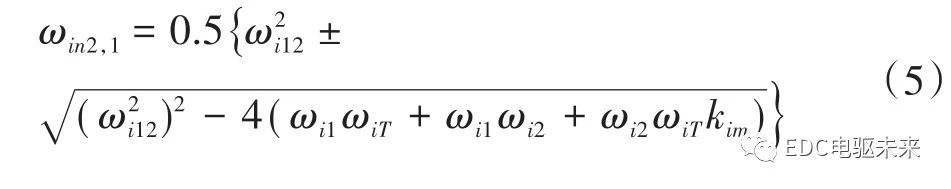
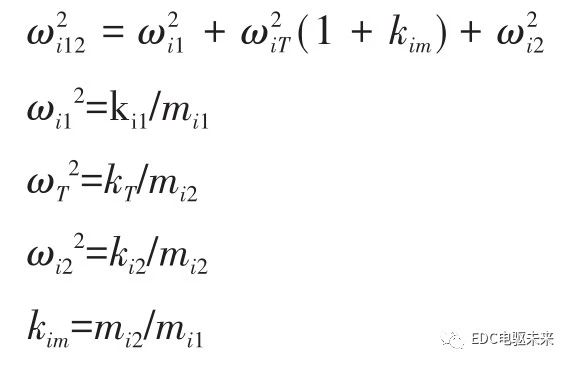
对应TE（t）的不同阶次的激励，式（4）作为常微分方程，有解析解[6]
式中，a1、a2分别为振动加速度。
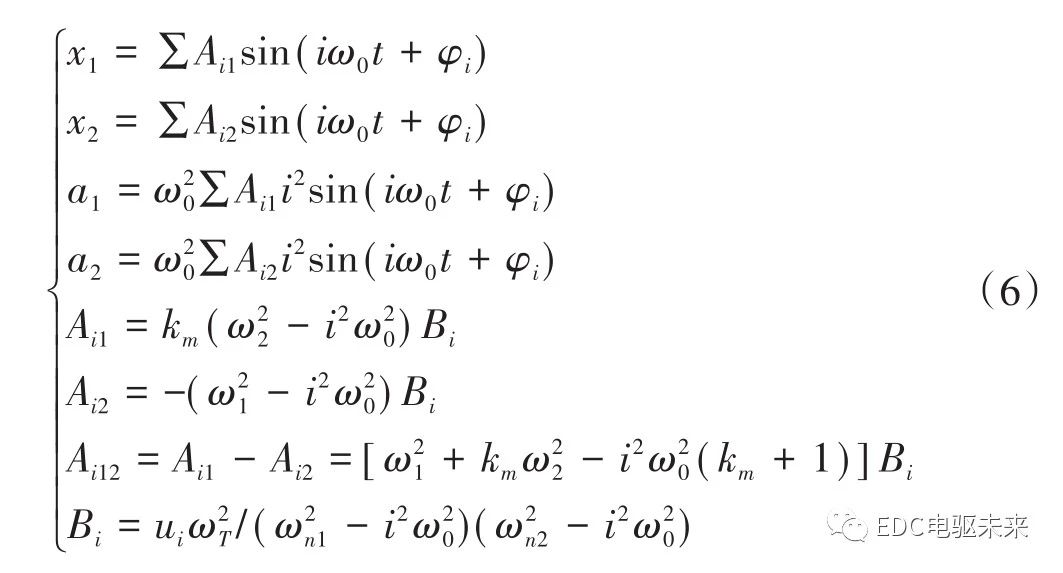
齿轮啮合的动态作用力FT（t）为
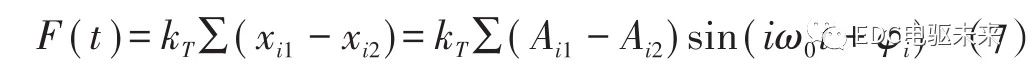
作用力FT（t）直接反映振动强度，可作为齿轮振动和噪声的评价指标。这就建立了齿轮振动与激振源—传动误差的函数关系。可以看到，振动与传动误差的频谱幅值和啮合刚度kT成正比。
不仅如此，通过轴承作用到箱体和地基上，形成箱体和基础的振动响应。对轴承和箱体的激振力为
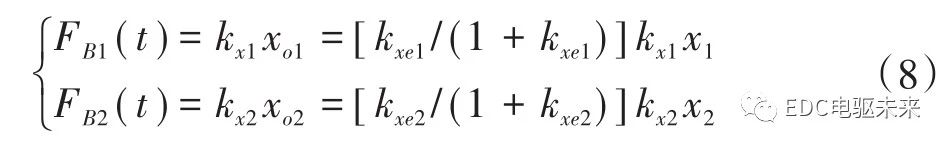
这也就建立了轴承与箱体振动与激振源—传动误差的函数关系。
3 强迫振动的参数影响分析
在上节中，通过对齿轮啮合过程中传动误差激励下的齿轮振动系统的响应分析，得到了传递误差激励下的振动方程解析解。在解析解中存在质量、刚度等影响因素，利用式（6）、式（7）分析质量、刚度等参数对传动误差的响应影响。
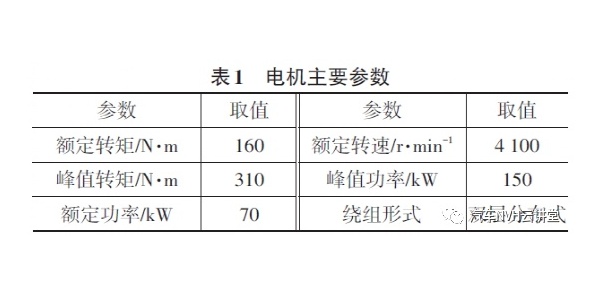
针对某型号的电动汽车减速器高速齿轮进行分析，齿轮基本参数同上，其他参数如表1所示。
表1 齿轮传动相关参数
传动误差频谱（图4）
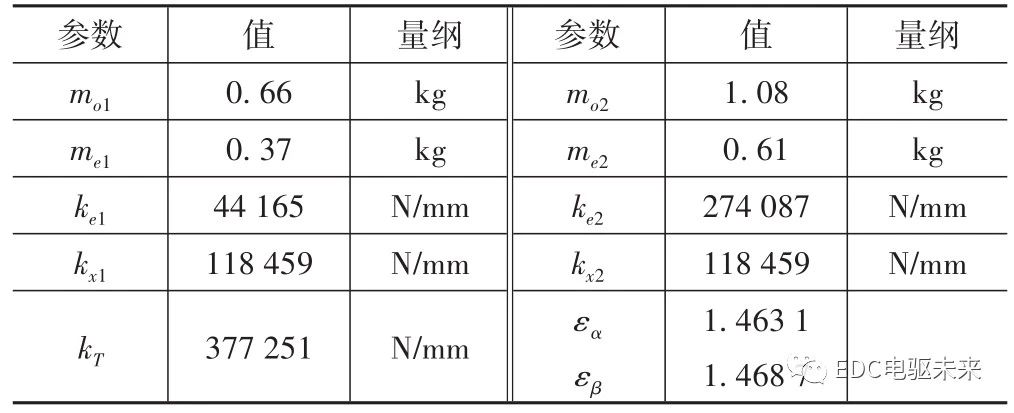
ui=[2.53，3.51，0.01，0.02，0.01]μm（i=1，2，3，4，5）
齿轮基频为
ω0=2πn1z1/60
式中，n1为输入轴的转速，r/min。
本节以分析齿轮传动误差引起的传动系统强迫振动相对振幅Ai12=Ai1-Ai2作为振动评价指标。针对前文中的齿轮参数进行分析，假设初始相位φi=0。以下分析均以12 000 r/min为例进行分析。
计算表明，由于式（4）中的mei2ω02＞＞kei和 kxi，所以，kxei≈mei/moi，阶次 i对等效刚度 ki1、ki2和固有频率ωn1，2的影响很小，可以认为是常数。
计算得到：ωn1=15 752.8 Hz、ωn2=53 604.8 Hz，临界频率ωn=50 621.6 Hz[7-8]。
但阶次i对式（6）中的振幅影响很大，见图7。
图7 阶次i对振幅Ai的影响
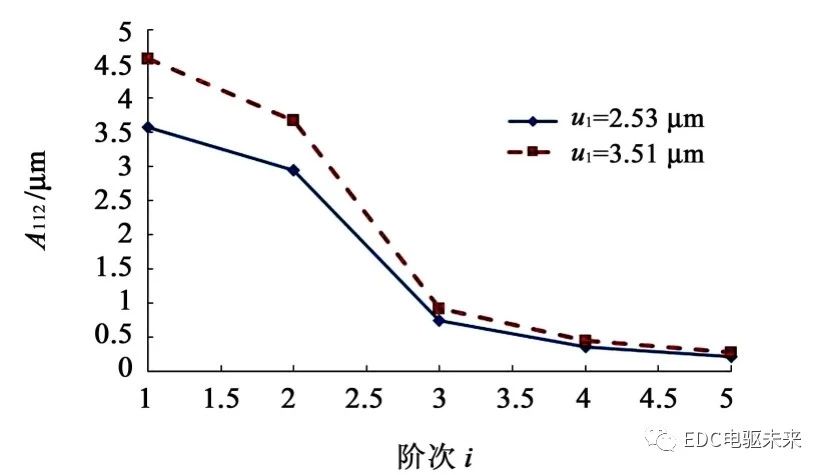
在图7中，阶次i对振幅的影响随着阶次i的增大，依次递减，且1、2阶次处振幅较大，因此，在对传动误差的激励响应分析时，一般取1、2阶次的振幅进行分析评价。
图8 等效刚度kei1对相对振幅Ai12的影响
图9 等效刚度kxi1对相对振幅Ai12的影响
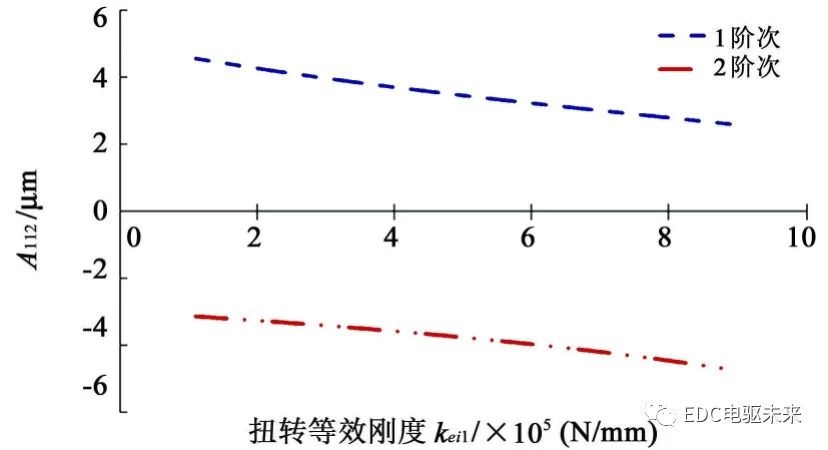
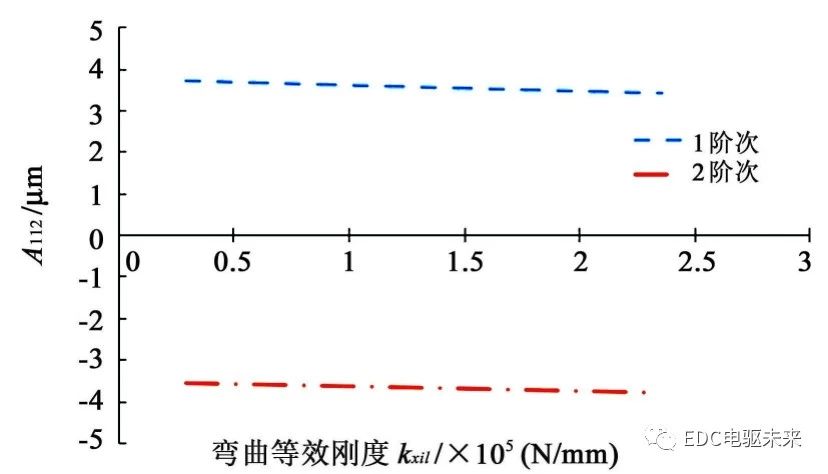
对不同的扭转等效刚度kei1、kxi1进行分析，取1、2阶次的相对振幅Ai12作为评价指标，从图8、图9可以看出，在同一转速下，扭转等效刚度kei1、弯曲等效刚度kxi1对TE的激励响应Ai12在不同阶次的影响呈现线性变化。
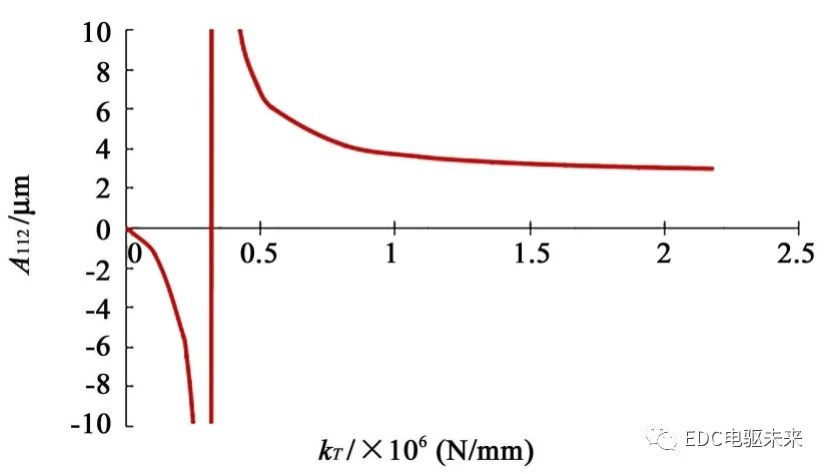
对齿轮的啮合刚度kT取不同的数值，以传动误差的1阶次u1激励下的1阶相对振幅A112作为评价指标，通过图10可以看出，在0.29倍kT时，激振频率ω0与齿轮系统的固有频率ωn2相同，引起共振；齿轮啮合刚度K＜0.29kT时，A112的幅值绝对值逐渐增大，齿轮啮合刚度K＞0.29kT时，A112的幅值绝对值逐渐减小，并趋于平缓。
图10 啮合刚度kT对相对振幅Ai12的影响
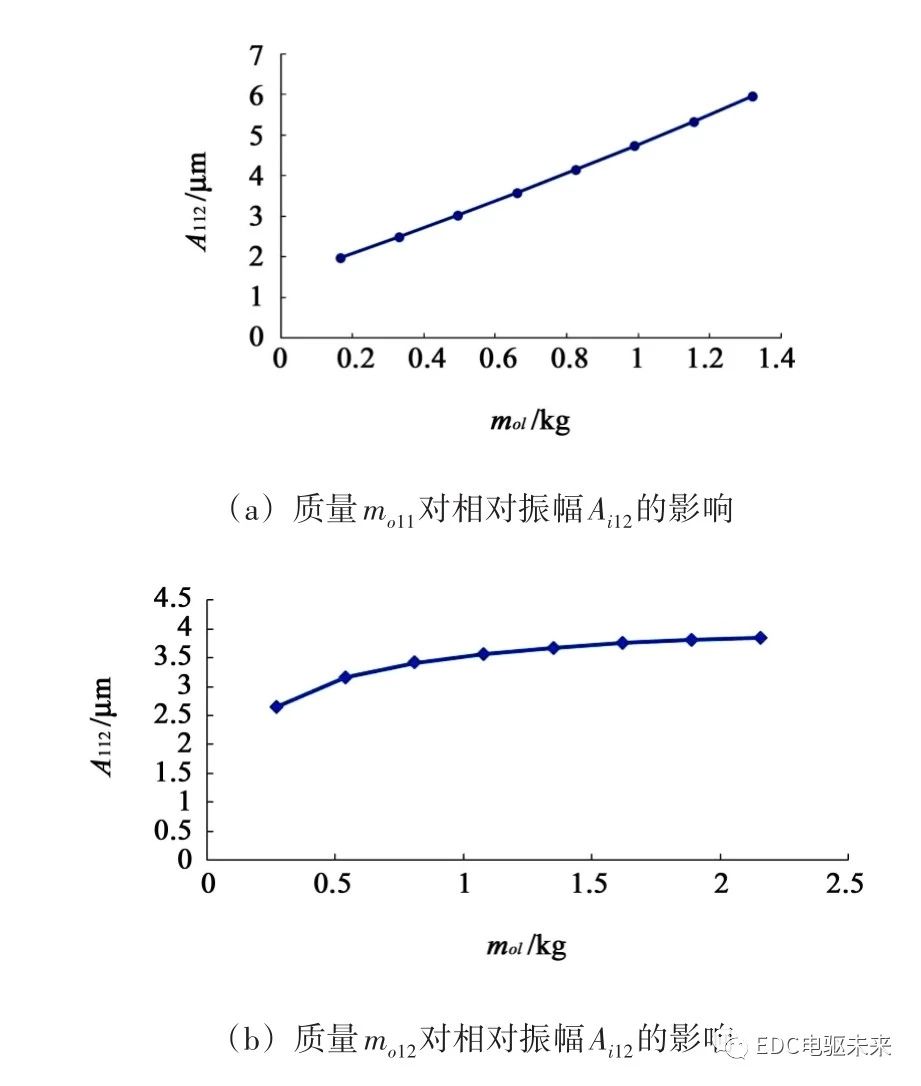
对齿轮质量mo进行分析，A112作为评价指标，由图11可知，随着mo11、mo12的增大，A112也呈现增大的趋势。对比图11（a）和图11（b）可知，A112随着mo12的增大较为缓慢。
图11 质量mo1i对相对振幅Ai12的影响
4 结论
（1）分析了齿廓修形和螺旋线修形后，对齿轮变形和传动误差的影响，提出了齿轮变形和传动误差优化的计算方法。
（2）利用系统传动误差频谱特性和强迫振动的频率特性，巧妙地将齿轮多自由度振动模型简化为双质量振动模型，得到了齿轮传动误差激励下的齿轮振动的解析解。
（3）建立了齿轮系统的质量、刚度、传动误差频谱与齿轮振动频谱的函数关系，得到了轮齿振动作用力、对轴承与箱体的振动作用力等关键的振动评价参数，这对减速器的NVH问题的分析与解决提供了明确、可靠的方法。
（4）分析传递误差激励下不同参数对齿轮传动系统的影响，为齿轮传动系统的优化设计提供指导。
- 下一篇：万向节附加弯矩对汽车NVH性能影响
- 上一篇：转向系统抖动机理简介
广告
最新资讯
-
NVIDIA 收购 GPU 编排软件提供商 Run:ai
2024-04-26 17:32
-
在亚洲最大车展见证 AI 推动未来交通运输业
2024-04-26 17:07
-
《GB/T 15385-2022 气瓶水压爆破试验方法》
2024-04-26 16:51
-
直播｜中国汽研：大倾角座椅下的乘员安全研
2024-04-26 16:35
-
采埃孚亚太区最大安全气囊生产基地在武汉投
2024-04-26 16:29
广告
广告
