广告
万向节附加弯矩对汽车NVH性能影响
2019-06-03 23:28:13· 来源：EDC电驱未来
在前置后驱的车辆中，传动轴是必不可少的动力传递元件。万向节的力矩不平衡特性使传动轴在旋转时产生振动，这些振动通过中间支承传递至车内，进而影响车辆的乘坐
在前置后驱的车辆中，传动轴是必不可少的动力传递元件。万向节的力矩不平衡特性使传动轴在旋转时产生振动，这些振动通过中间支承传递至车内，进而影响车辆的乘坐舒适性与整车的NVH性能。因此，迫切需要对传动轴进行优化与改进，提升汽车乘坐舒适性与整车NVH性能。
万向节作为传动轴的重要组成部分，对传动轴的NVH特性起着至关重要的作用。闫公哲[1]创新了一种7沟道球笼式等速万向节，在不同的工况下对创新结构和传统结构两种球笼式等速万向节的轴间摆角、转速以及钢球对内外沟道的作用力和磨损情况等之间的关系及其变化规律，理论结果表明：创新结构的球笼式等速万向节的动力学性能要明显优于传统结构。田海兰等[2]基于ADAMS和ANSYS进行动态特性仿真分析，采用理论计算和运动仿真相结合的方法，得到了十字轴万向节输出轴角加速度和角速度曲线。Jian-Wei Lu等[3]针对十字轴万向节的十字轴颈的装配间隙建立了动力学模型，并对万向节进行了传动特性分析。前人对万向节传动特性的研究为本研究的传动轴优化改型提供了理论基础。
对于由万向节和轴组成的传动轴或传动系统的振动特性、稳定性等，国内外学者均有较为成熟的研究。赵骞等[4]针对十字万向节传动轴激励导致的汽车振动噪声现象，探讨了从激励、传递路径到响应3方面优化振动噪声问题的方法，并对方法进行了应用介绍。GökhanBulut[5]对单十字轴万向节传动系统进行了扭转振动的动力学稳定性分析，将分析结果以Mathieu-Hill方程与Strutt-Ince图表展示出来。李宁等[6]建立双十字轴万向节传动轴的转速比和转角方程，定量分析了相位角对转速比的影响，得出了传动轴相位角与传动面夹角相等且方向相反时为最佳相位角的结论。
以上研究均局限于对十字轴万向节串联系统的研究，对十字轴万向节串联形成的传动系统的优化进入了瓶颈阶段，难以使其性能再有较大提升，严重制约着整车NVH性能的提升。而采用球笼万向节与十字轴万向节混联方式的传动轴是一种新的探讨，迫切需要对混合使用球笼万向节与十字轴万向节的传动轴进行振动性能的研究。
1 万向节传递特性分析
1.1 十字轴万向节传递特性分析
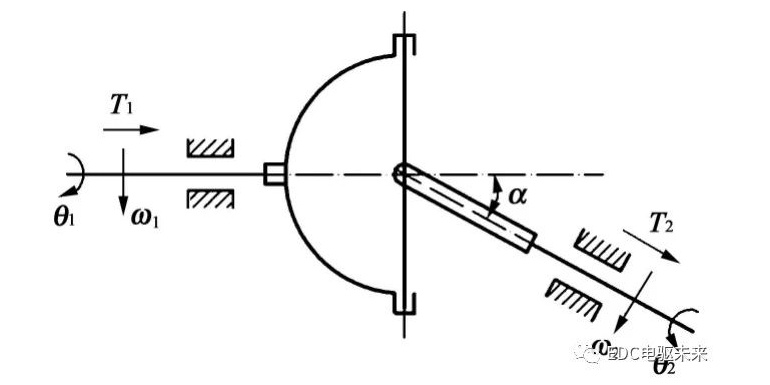
十字轴万向节为非等速万向节，当输入轴与输出轴之间存在夹角时，输出转速和输出转矩均会出现周期性波动，波动幅值随着夹角的增大而增大。对于单个十字轴万向节，其简化结构如图1所示。
图1 十字轴万向节结构简图
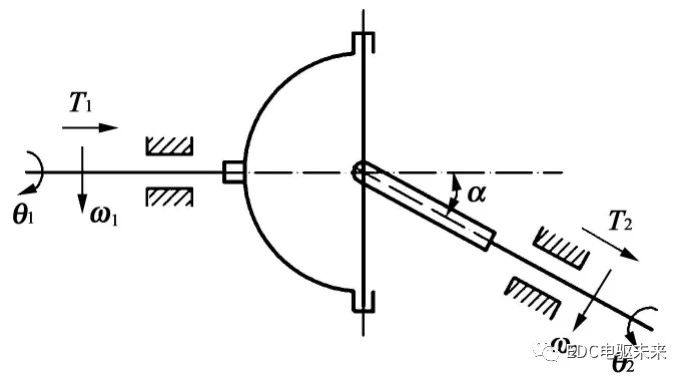
图1中，θ1为输入轴转角；θ2为输出轴转角；ω1为输入转速；ω2为输出转速；α为输入轴与输出轴之间的夹角；T1为输入转矩；T2为输出转矩。
根据十字轴万向节的运动特性，可得到输出转速ω2与输入转速ω1的关系为[7]
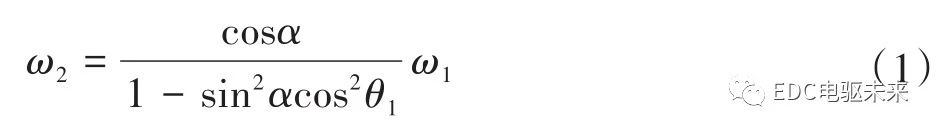
在不考虑功率损失的情况下，可求得输出转矩T2与输入转矩T1的关系为
输入轴与输出轴之间的夹角α不为0时，T1与T2不共线，不满足力平衡条件，所以机构上必然存在附加弯矩与其平衡。输入轴附加弯矩T′1与输出轴附加弯矩T′2可描述为
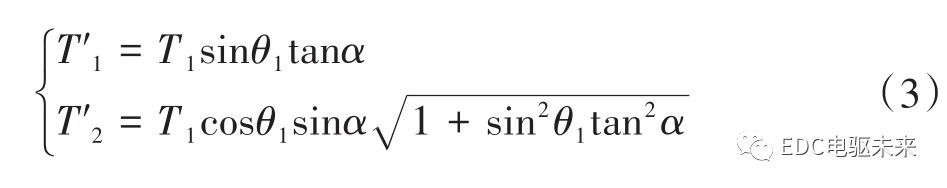
1.2 球笼万向节传递特性分析
球笼式万向节属于等角速度万向节，对于单个Birfield球笼万向节，其结构如图2所示。
图2 Birfield球笼万向节剖视图
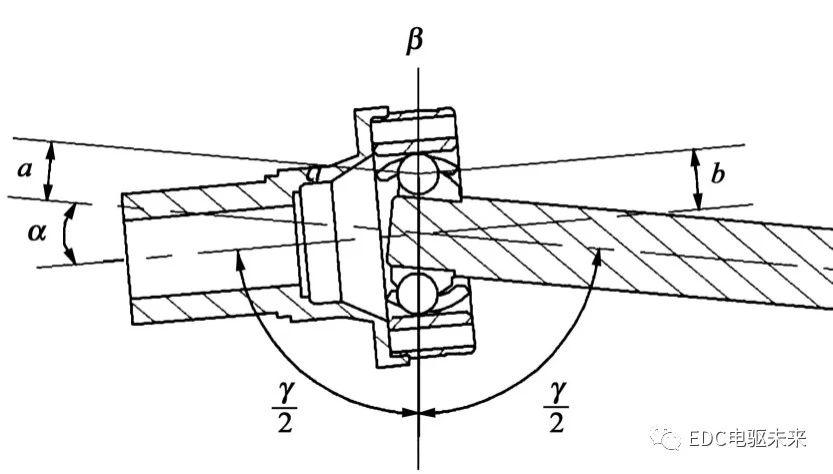
图2中，a为钢球球心到输出轴的距离；b为钢球球心到输入轴的距离；β为轴间夹角平分面；α为输出轴与输入轴之间夹角。
在输入轴与输出轴之间的夹角α不为0时，Birfield球笼万向节中的6个钢球形成的平面始终保持在轴间夹角平分面β上。对于每个钢球，距离a与距离b相等，符合万向节等速传递特性。因此，有
对比十字轴万向节与Birfield球笼万向节的特性分析结果可知，十字轴万向节的输出轴角速度ω1、输出转矩T1以及附加弯矩均存在与输入转角θ1相关的周期性波动；而Birfield球笼万向节输出轴角速度ω2、输出转矩T2以及附加弯矩均为定值，消除了由以上参数周期性波动而引起的振动，有利于提高传动系统运转的稳定性。
2 二段式传动轴中间支承处激振力分析
2.1 二段式传动轴布置方案
对于前置引擎后轮驱动的车辆，传动轴是将变速器的动力传递至主减速器的重要部件。所研究车型的传动轴为二段式传动轴，轴管之间采用万向节连接，并设置有中间支承，以保证传动轴运行平稳、安全。由于传动轴中间支承存在橡胶减振环，在万向节附加弯矩的作用下，传动轴在中间支承处产生的振动与噪声最为明显，这些振动与噪声通过中间支承传递至车内，影响整车的NVH性能。
图3为所研究车型的原传动轴，即3十字轴万向节传动轴。
图3 3十字轴万向节传动轴
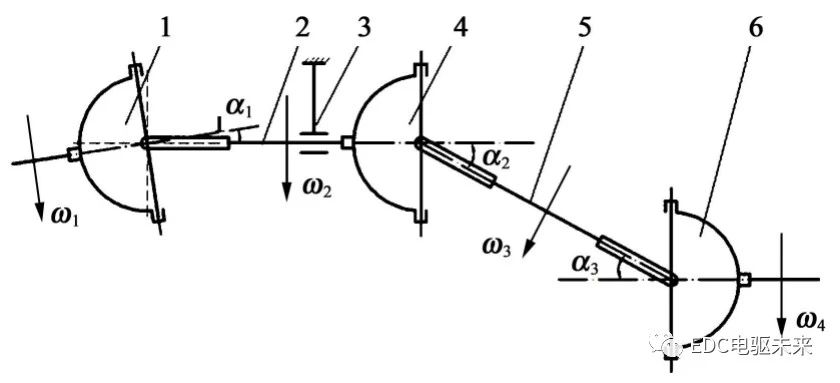
图3中，1为第1万向节，2为轴1，3为中间支承，4为第2万向节，5为轴2，6为第3万向节。
万向节附加弯矩在传动轴中间支承处的激振力以第2万向节的附加弯矩贡献最大。Birfield球笼万向节输入轴与输出轴附加弯矩恒定，若将3个十字轴万向节传动轴的第2十字轴万向节替换为Birfield球笼万向节，则传动轴在中间支承处的激振力将得到减弱。经改型所得的Birfield球笼万向节传动轴示意简图如图4所示。
图4 Birfield球笼万向节传动轴示意
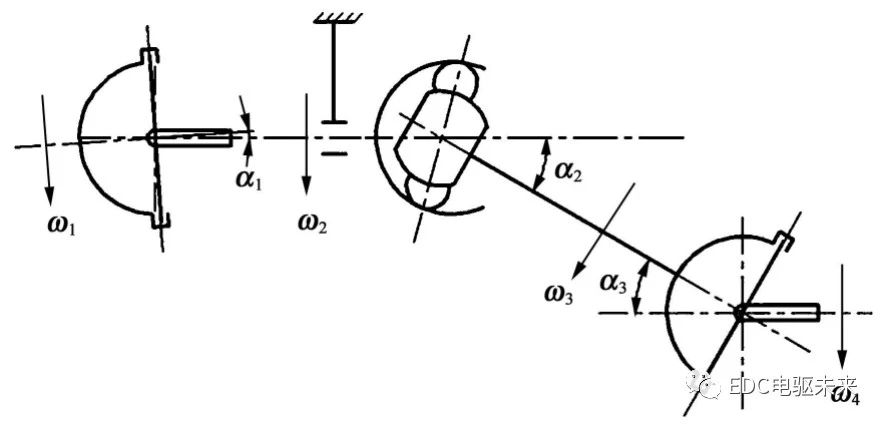
2.2 3十字轴万向节传动轴中间支承处激振力分析
作用于3个十字轴万向节传动轴中间支承处的万向节附加弯矩有：第1个十字轴万向节输出轴的附加弯矩、第2个十字轴万向节输入轴的附加弯矩、第2个十字轴万向节输出轴的附加弯矩、第3个十字轴万向节输入轴的附加弯矩。第1个十字轴万向节输入轴由于与变速器为滑动花键连接，其附加弯矩作用于花键轴；第3个十字轴万向节输出轴为法兰，连接于主减速器的主齿法兰，其附加弯矩作用于主减速器主动齿轮上的两个支承轴承。为了便于计算和分析，假设中间支承轴线与轴1水平重合。
图5 3十字轴万向节传动轴轴管长度示意
图5中，L1为第1万向节到中间支承的水平距离；L2为中间支承到第2万向节的水平距离；L3为中间支承到第3万向节的水平距离。
依据式（2）、式（3）可获得作用于3个十字轴万向节传动轴中间支承处的附加弯矩有
式中，T′jin为第j万向节输入轴附加弯矩；T′jout为第j万向节输出轴附加弯矩。
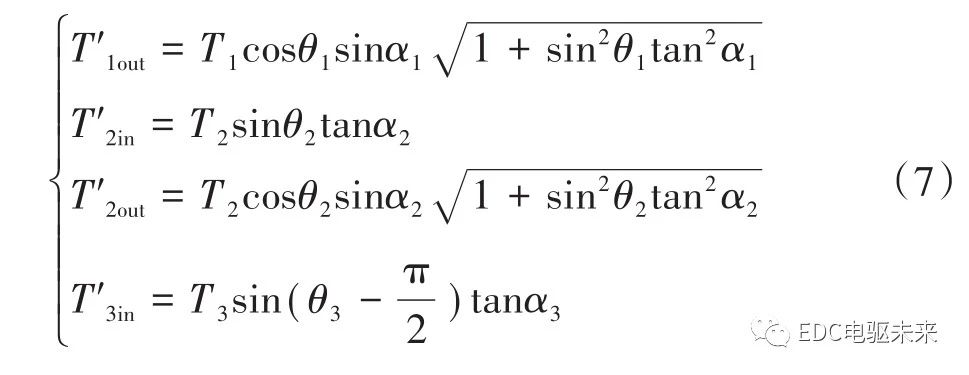
根据式（1）可得各转角关系为
第3个十字轴万向节输入轴的附加弯矩通过第2个万向节作用于中间支承处，忽略第2个万向节的摩擦与振动，依据式（9）可分别计算各附加弯矩在传动轴中间支承处的作用力。
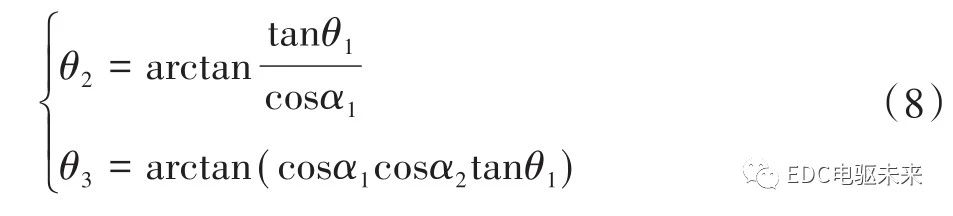
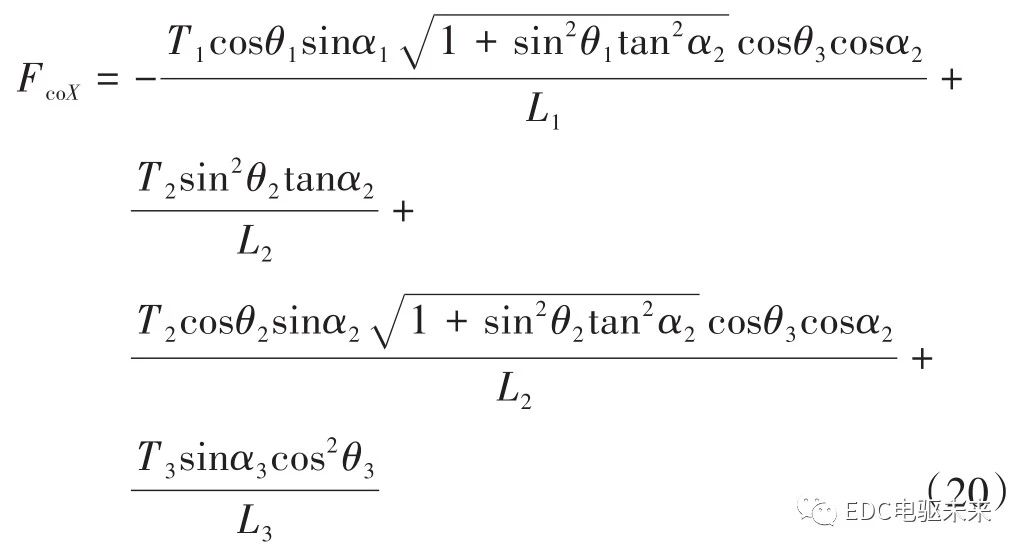
式中，F′jin为第j万向节输入轴在中间支承处的作用力；F′jout为第j万向节输出轴在中间支承处的作用力。
将各万向节附加弯矩在传动轴中间支承处的作用力分解为垂直方向Y与水平方向X的激振力，如式（10）所示。
式中，F′jinX为F′jin在X方向的分解力；F′jinY为F′jin在Y方向的分解力；F′joutX为F′jout在X方向的分解力；F′joutY为F′jout在Y方向的分解力。
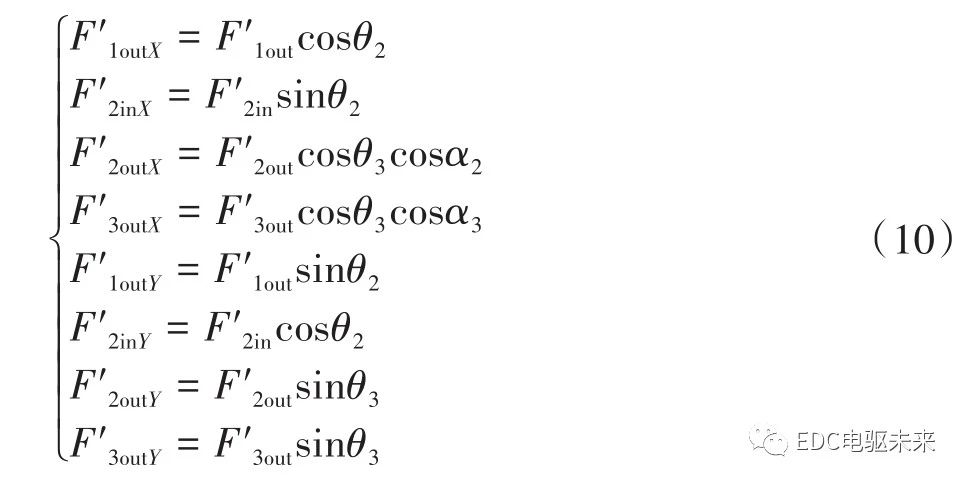
依据3个万向节的布置方式可以得到，万向节附加弯矩在3十字轴万向节传动轴中间支承处X方向产生的等效激振力FcoX为
万向节附加弯矩在3十字轴万向节传动轴中间支承处Y方向产生的等效激振力FcoY为
2.3 Birfield球笼万向节传动轴中间支承作用处激振力分析
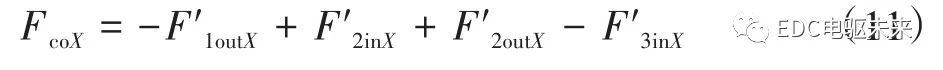
Birfield球笼万向节传动轴中间支承处激振力的来源与3十字轴万向节传动轴的相同，但是由于前者十字轴万向节相位布置情况的调整和Birfield球笼万向节动力特性的特殊性，Birfield球笼万向节传动轴中间支承处的激振力与十字轴万向节传动轴的不相同。
图6 Birfield球笼万向节传动轴轴管长度示意
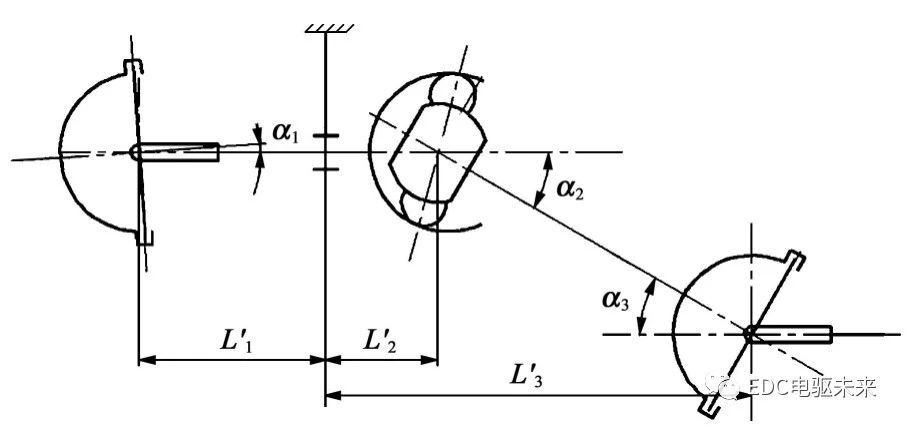
图6中，L′1为第1万向节到中间支承的距离；L′2为中间支承到第2万向节的距离；L′3为中间支承到第3万向节的距离。
依据式（5）、式（6）可获得作用于Birfield球笼万向节传动轴中间支承处的附加弯矩有
根据式（1）、式（4）可得各转角关系为
因为Birfield球笼万向节附加弯矩大小与方向不随着旋转角度的变化而变化，因此，对于Birfield球笼万向节输入轴与输出轴上附加弯矩在水平方向X与垂直方向Y的投影弯矩有
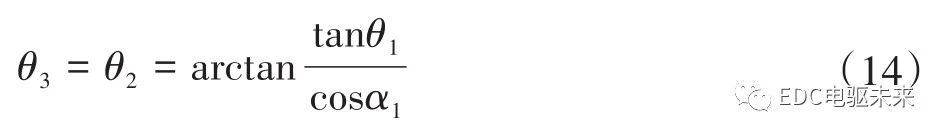
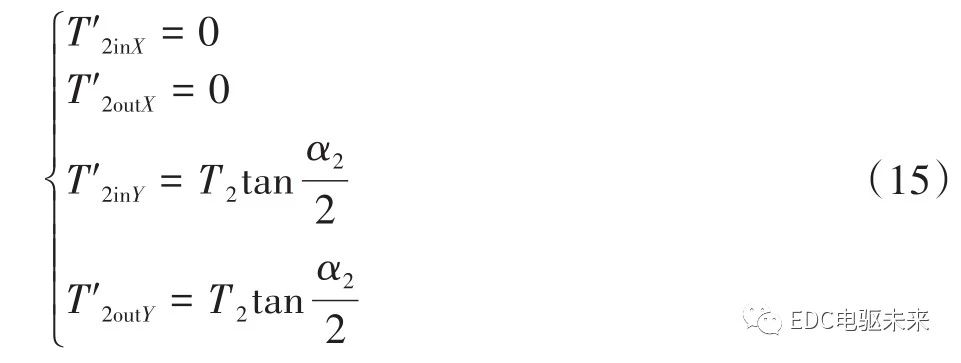
计算附加弯矩对传动轴中间支承处的作用力，分解到X方向的结果如式（16）所示，分解到Y方向的结果如式（17）所示。
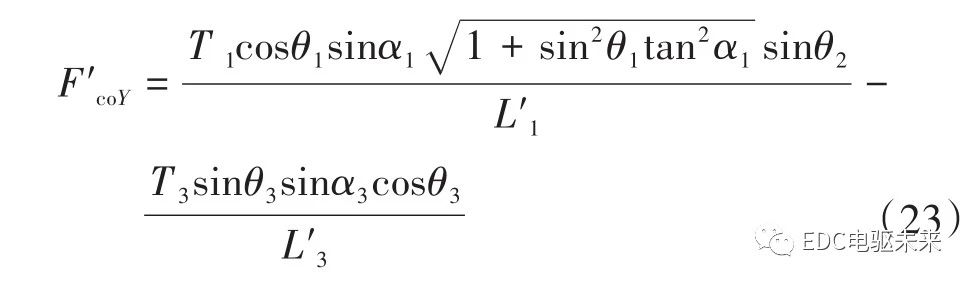
依据3个万向节的布置方式可以得到，万向节附加弯矩在Birfield球笼万向节传动轴中间支承处水平方向X产生的等效激振力F′coX有
万向节附加弯矩在Birfield球笼万向节传动轴中间支承Y方向产生的等效激振力F′coY有
2.4 两种传动轴中间支承受力对比分析
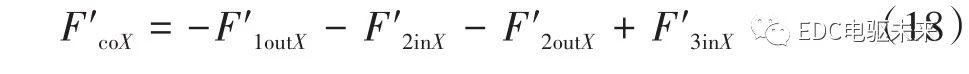
联立式（7）、式（9）、式（10）、式（11）可求得万向节附加弯矩在3十字轴万向节传动轴中间支承处X方向产生的等效激振力FcoX为
联立式（7）、式（9）、式（10）、式（12）可求得万向节附加弯矩在3十字轴万向节传动轴中间支承处Y方向产生的等效激振力FcoY为
联立式（13）、式（15）、式（16）、式（18）可求得万向节附加弯矩在Birfield球笼万向节传动轴中间支承处X方向产生的等效激振力F′coX为
联立式（13）、式（15）、式（17）、式（19）可求得万向节附加弯矩在Birfield球笼万向节传动轴中间支承处Y方向产生的等效激振力F′coY为
激振力对中间支承处产生激励，使中间支承产生振动，中间支承再通过底盘将振动传递至车内。激振力越大，车内地板振动越剧烈。式（20）、式（21）、式（22）、式（23）比较复杂，难以直观看出激振力与传动轴转动过程的关系。本研究以车辆在50 km/h速度匀速行驶时为例，根据所研究车型参数可计算出传动轴负载T3为87 N·m。代入所研车型的已知参数 α1、α2、α3，L1、L2、L3，其中，α2为多个数值，分别取3°、4°、5°、6°、7°。以θ1为自变量，联立式（8）、式（20），在MATLAB中即可求解出激振力 FcoX与 θ1的变化关系曲线，截取 θ1在 0°～720°的变化范围曲线，如图7所示，图中，5条曲线分别代表α2分别取3°、4°、5°、6°、7°时的曲线。同理，联立式（8）、式（21），在MATLAB中即可求解出激振力FcoY与θ1的变化关系曲线，如图8所示；联立式（14）、式（22），在MATLAB中即可求解出激振力F′coX与θ1的变化关系曲线，如图9所示；联立式（14）、式（23），在MATLAB中即可求解出激振力F′coY与θ1的变化关系曲线，如图10所示。
图7 激振力FcoX与θ1关系曲线
图8 激振力FcoY与θ1关系曲线
图9 激振力F′coX与θ1关系曲线
图10 激振力F′coY与θ1关系曲线
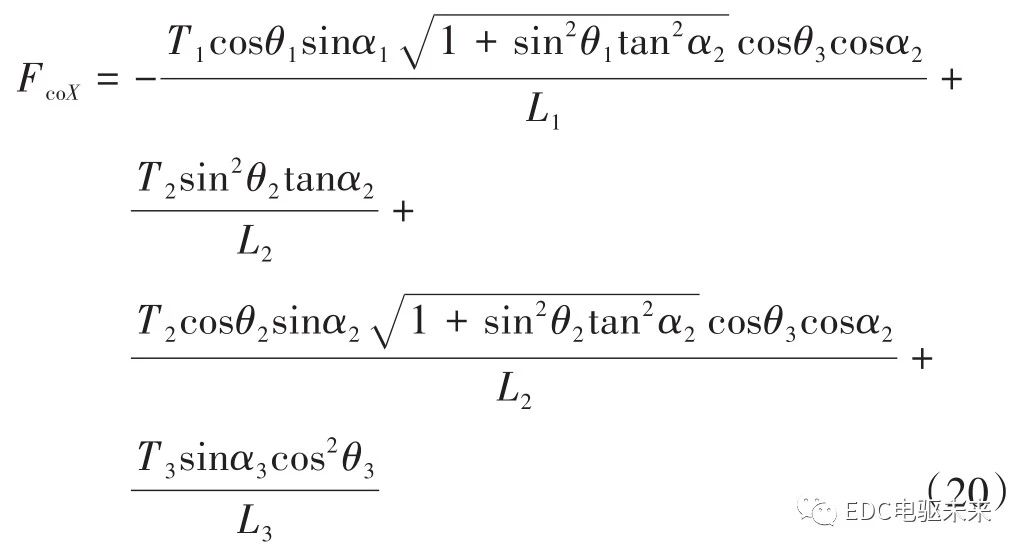
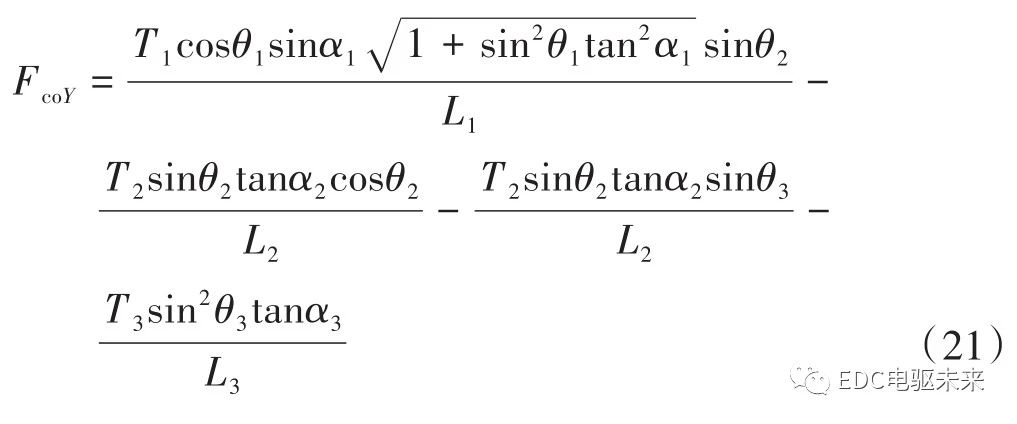
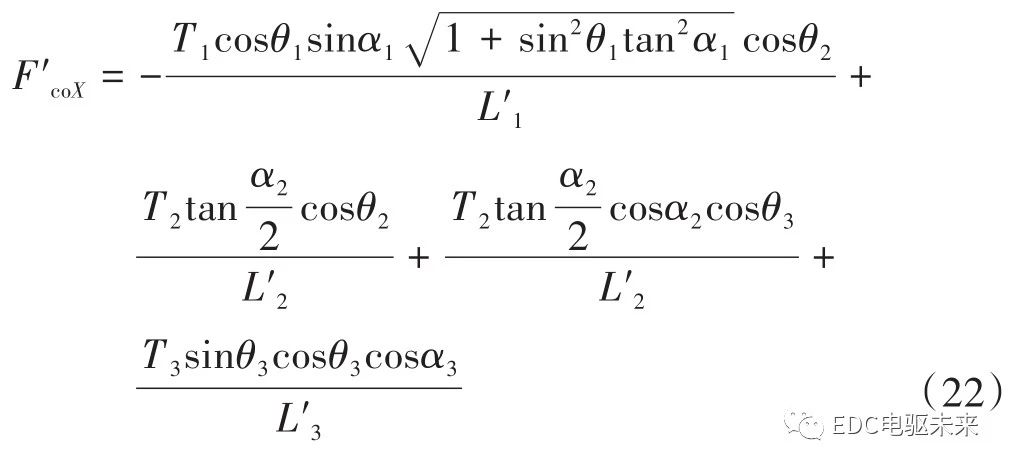
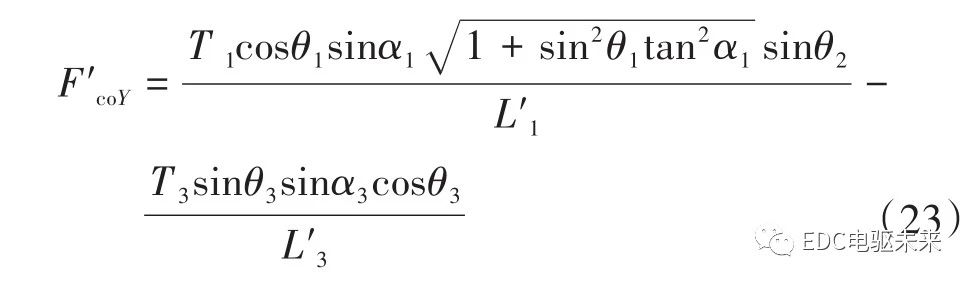
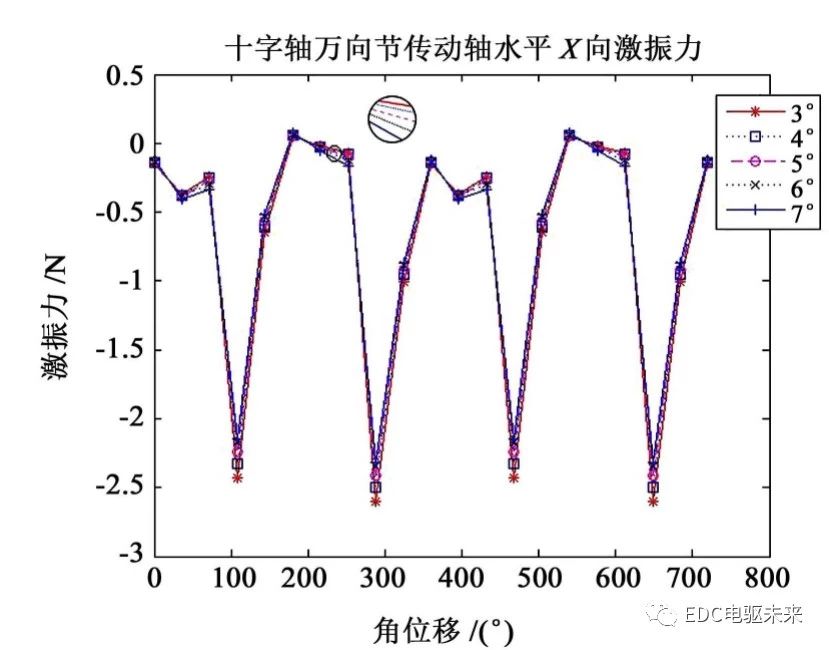
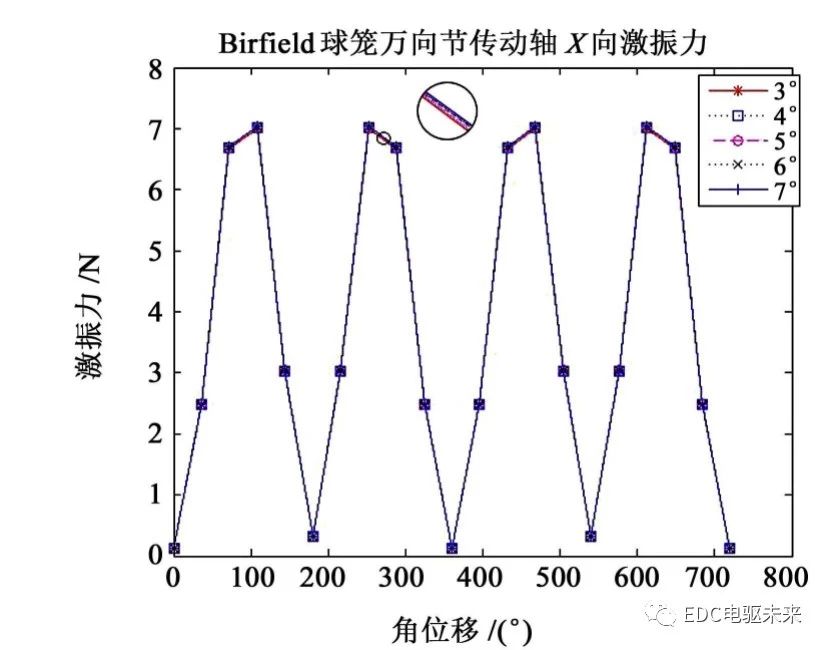
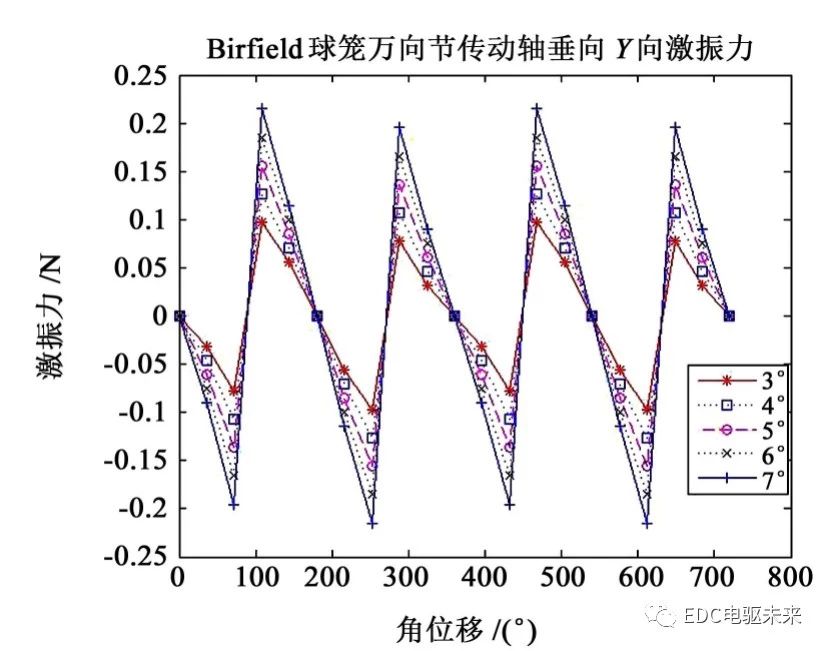
对比图7与图9可知，随着夹角α2的变化，3十字轴万向节传动轴X方向激振力存在一定的变化，而Birfield球笼万向节传动轴X方向激振力的变化微小，可以忽略。虽然Birfield球笼万向节传动轴X方向的激振力值比3十字轴万向节传动轴的大，但是，其激振力的激振方式接近梯形波单向激振，较3十字轴万向节传动轴的三角波双向激振更柔和，有效地降低了振动加速度。对比图8与图10可知，与3十字轴万向节传动轴相比，Birfield球笼万向节传动轴在Y方向上的激振力得到极大削减，优化了传动轴总成中间支承对车辆地板的垂向冲击，减少了车辆地板振动，降低了车内噪声。
综合对结果的分析可知，通过将原传动轴的第2十字轴万向节替换为Birfield球笼万向节和改进轴叉相位角获得Birfield球笼万向节传动轴。改型后的获得Birfield球笼万向节传动轴将中间支承处Y方向的激振力转移至X方向上，X方向的激振力变得更柔和，极大地减小了Y方向的激振力，传动轴中间支承处的振动与噪声得到衰减，进而提升了整车NVH性能。
3 试验验证
针对以上两种传动轴的理论分析结果进行试验验证。试验采用同一辆车，分别安装两种传动轴进行试验。依据企业自行制定的标准，在A级路面进行车辆振动与噪声性能评估实验，试验所用软件为LMSTestLab，如图11所示。
图11 LMSTestLab测试界面与信号采集集成设备
试验之前，将高灵敏度麦克风布置于中排座椅靠枕侧边，用以采集中间支承附近人耳所能感受到的噪声信号。利用测试软件对采集得到的噪声信号进行计算可得出传动轴阶次（1.21阶）噪声情况。在传动轴中间支承处的上方安装一位移传感器，用以测量传动轴中间支承处垂直方向的振动位移，由测试软件对采集得到的位移信号进行频域处理。由于原车3十字轴万向节传动轴在5挡全油门加速下振动与噪声较为严重，本试验工况为：5挡全油门加速。
3.1 车内噪声结果与分析
座位中排地板连接的是传动轴的中间支承支座，在车内噪声测试中，通常将中排噪声作为评价传动轴中间支承性能的主要指标，其也是评价传动轴整体性能的重要指标之一。图12所示为两种传动轴的车内中排噪声情况，图中，实线为3十字轴万向节传动轴车辆噪声情况，虚线为Birfield球笼万向节传动轴车辆噪声情况。
图12 车内中排噪声情况
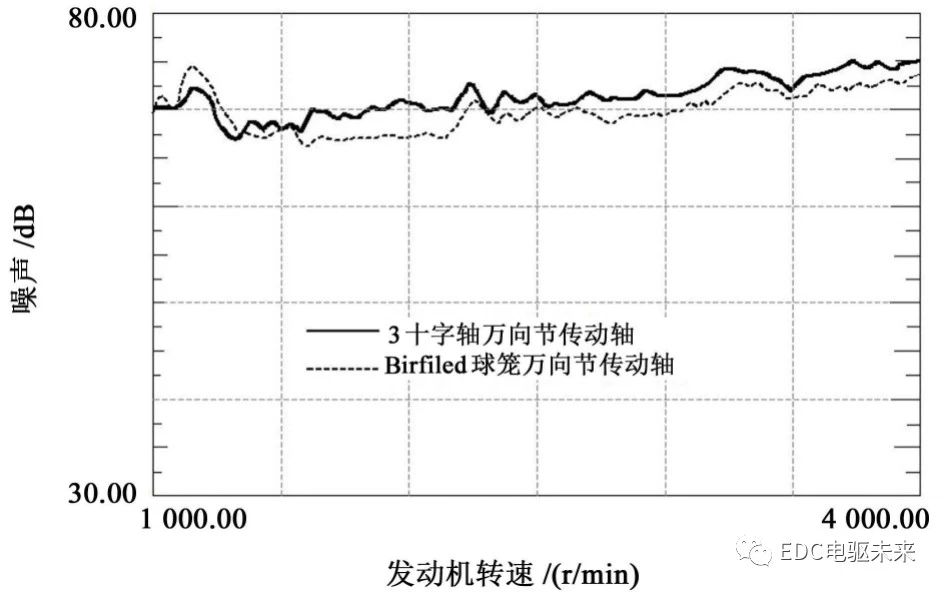
如图12所示，在低转速区由于动力匹配不平衡，车辆传动传动系统抖动明显，两车辆均出现明显的噪声波峰。在之后的加速过程中，两种车辆的噪声情况均较为平稳，而Birfield球笼万向节传动轴车辆的中排噪声明显低于3十字轴万向节传动轴，在中低速区域约降低5 dB；在中高转速区域约降低2 dB。验证了理论部分的Birfield球笼万向节传动轴使传动轴中间支承处的Y方向激振力得到极大地削弱，进而使振动与噪声得到削弱。由此可见，Birfield球笼万向节传动轴对车内噪声的降低有一定的促进作用，有利于提升整车的NVH性能。
3.2 阶次噪声结果与分析
由中排噪声提取出传动轴阶次噪声如图13所示，图中实线为3十字轴万向节传动轴车辆阶次噪声情况，虚线为Birfield球笼万向节传动轴车辆阶次（1.21阶）噪声情况。
图13 传动轴阶次噪声
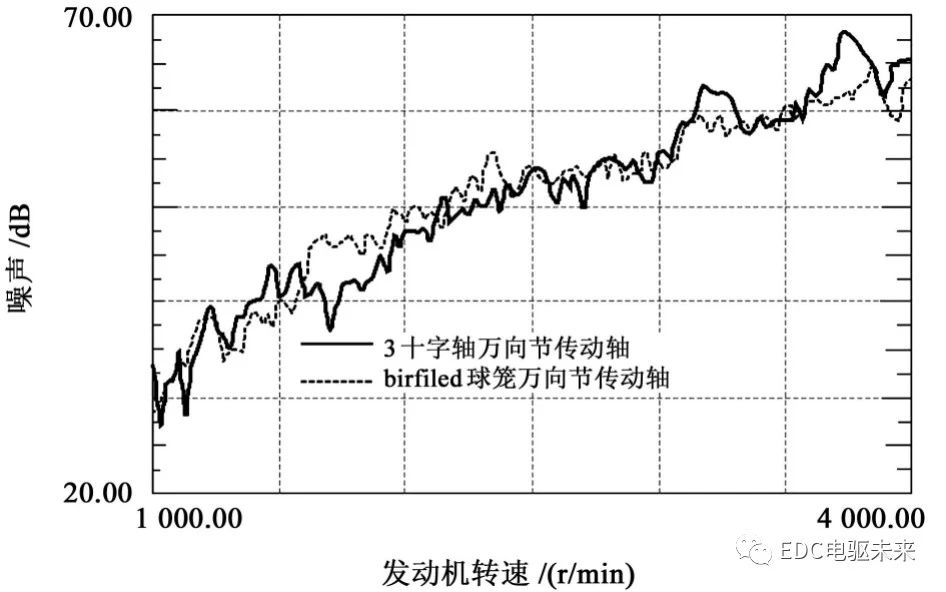
如图14所示，3十字轴万向节传动轴在1000r/min～4 000 r/min的整个转速区域中阶次噪声起伏明显，在3 000 r/min～4 000 r/min区域阶次噪声波动明显且出现两个峰值，阶次噪声偏大；Birfield球笼万向节传动轴在该工况下全转速区域中阶次噪声变化平稳，在1 500 r/min～2 500 r/min区域内阶次平均噪声较高，但阶次噪声波动较小。验证了理论部分Birfield球笼万向节传动轴的X方向激振力的激振方式接近梯形波单向激振，使激振力变得更柔和。可见，Birfield球笼万向节传动轴平稳的阶次噪声可以给乘客提供更好的乘坐舒适性，提升了整车的NVH性能。
3.3 传动轴中间支承处频谱结果与分析
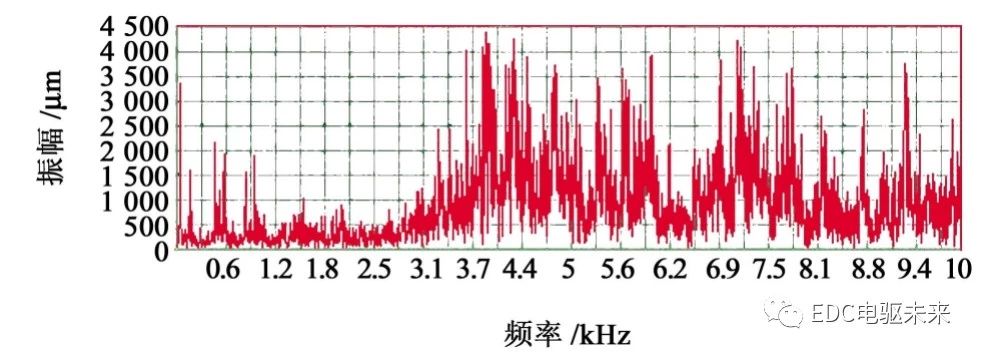
由测试软件分别对采集的信号进行频域处理可得两种传动轴的频谱。3十字轴万向节传动轴频谱如图14所示；Birfield球笼万向节传动轴频谱如图15所示。
图14 3十字轴万向节传动轴频谱
图15 Birfield球笼万向节传动轴频谱
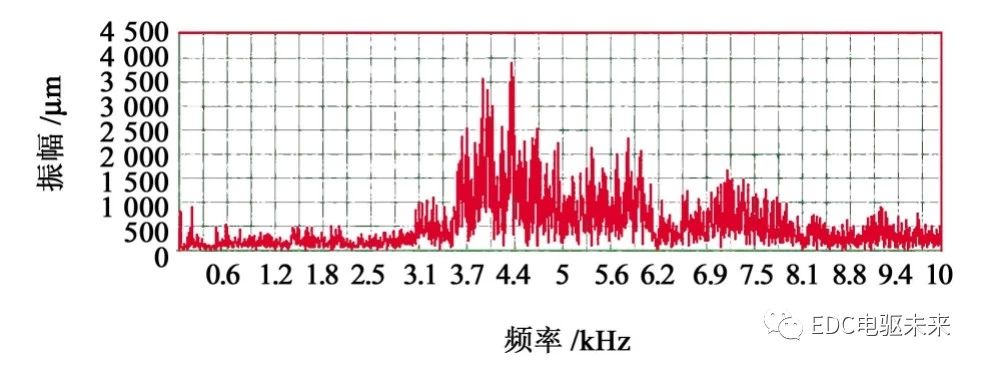
如图14所示，3十字轴万向节传动轴在0～1.2 kHz之间出现多次峰值，在3.1～10 kHz之间峰值较多，且振幅较大，振动较为激烈。如图15所示，Birfield球笼万向节传动轴在3.4～6.2 kHz之间峰值较多，但振幅较3十字轴万向节传动轴的小；其余频率的振幅较小，较为稳定。
通过以上分析可知，Birfield球笼万向节传动轴的振幅整体比3十字轴万向节传动轴的小，稳定性较好，有利于提升整车NVH性能。
4 结语
利用Birfield球笼万向节的等速传递特性，将3十字轴万向节传动轴的第2十字轴万向节改为Birfield球笼万向节，同时改变第3十字轴万向节的布置方式，获得Birfield球笼万向节传动轴。对两种传动轴中间支承处的激振力求解分析和试验验证。表明Birfield球笼万向节将原传动轴的Y方向激振力转移至X方向，使改型获得的Birfield球笼万向节传动轴X方向激振力变为接近梯形波的单向柔和激振力，Y方向激振力得到极大地削弱，进而使中间支承处振动与噪声得到削弱，同时阶次噪声变得更加平稳。对两种传动轴的频谱进行分析，结果表明，Birfield球笼万向节传动轴的振幅整体比3十字轴万向节传动轴的小、稳定性较好。改型后获得的Birfield球笼万向节传动轴有利于提升车辆的乘坐舒适些与整车NVH性能。
广告 
广告
最新资讯
-
智能网联公司与澳大利亚ANCAP开展技术交流
2025-02-24 16:14
-
《汽车轮胎干路面制动距离试验方法》等团体
2025-02-24 16:13
-
突然解散！又一智驾公司总部封楼！
2025-02-24 12:09
-
【直播预告】当"双碳"遇上高压快充：破局新
2025-02-24 12:08
-
直播｜车载高速以太网测试技术线上研讨会
2025-02-24 11:11
广告
广告
