寻找供应商
广告
首页 > 仿真与模拟 > 正文

驱动桥传动系典型工况下的一体化动力学仿真

2019-09-14 18:27:46·  来源：EDC电驱未来  
　
驱动桥是汽车总成中重要的组成部分，主要由主减速器总成、差速器、半轴和驱动桥壳等部分构成，其主要作用是将由传动轴传导来的转矩和力通过半轴分配到左右车轮，
驱动桥是汽车总成中重要的组成部分，主要由主减速器总成、差速器、半轴和驱动桥壳等部分构成，其主要作用是将由传动轴传导来的转矩和力通过半轴分配到左右车轮，实现降低速度增大转矩的作用，同时改变转矩方向；当车辆转弯行驶时，差速器开始发挥差速作用，从而让左右驱动轮能以不同的速度转动实现转向。驱动桥中主减速器和差速器的性能会直接影响到车辆的整体性能表现，多数著作大都单独研究主减速器或者差速器的动态性能，少有将两者的装配总成一起研究的。

本文基于三维软件UG，完成了驱动桥主减速器主从动锥齿轮、差速器行星齿轮和半轴齿轮的三维几何模型的创建，得到了无干涉装配模型，再以通用的Parasolid图形交换格式导入到动力学软件Ad⁃ams中完成了驱动桥虚拟样机模型的构建，并在此驱动桥虚拟样机模型中融入Hertz接触理论，进而分析了驱动桥在不同工况下的运动学和动力学特性，为进一步研究驱动桥主减速器和差速器齿轮运动学和动力学特性提供了可靠依据，同时也为降低汽车后桥主减速器和差速器振动，优化其性能提供了技术支持。

1 三维模型的建立

1.1 差速器模型建立

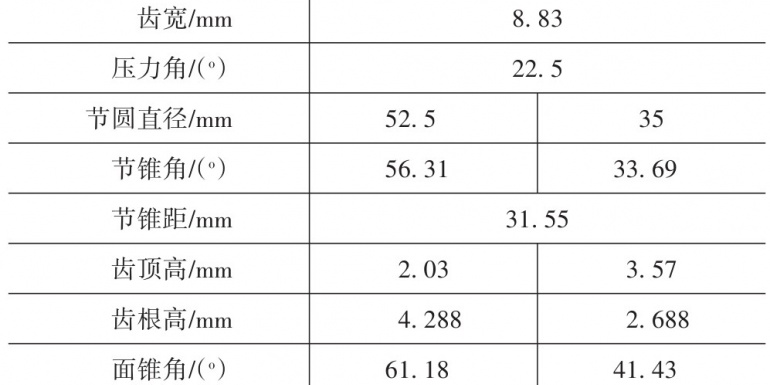
本文所述差速器包括4个行星齿轮、2个半轴齿轮和1个十字轴，采用参数化建模的方式，在UG里插入表达式，分别得到行星齿轮和半轴齿轮的三维模型，具体参数如表1所示。

表1 差速器齿轮主要参数

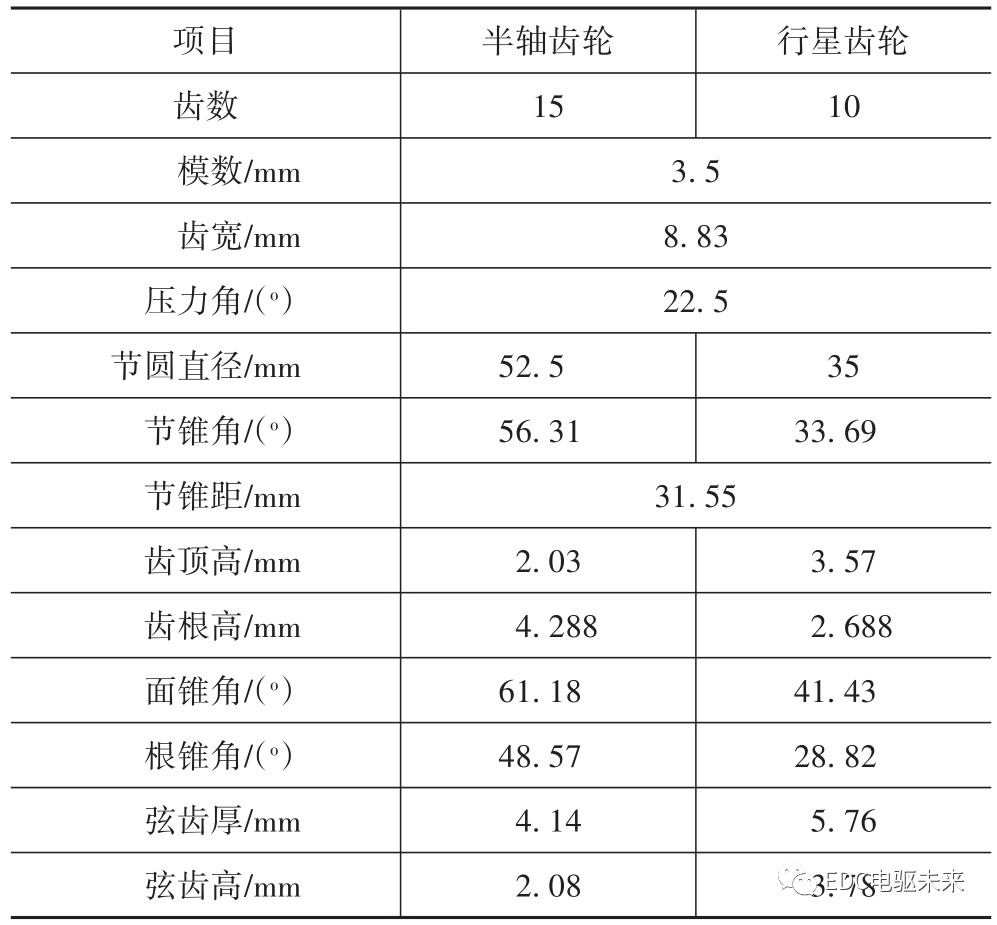
得到的差速器三维模型如图1所示。
图1 差速器三维模型

1.2 准双曲面齿轮几何模型的建立

由于准双曲面齿轮是弧齿锥齿轮中最复杂的一种，传统的建模方法难度极高，而且没有结合实际加工参数，准确性没有得到验证。本文以小轮左旋、展成法加工，大轮右旋、成形法加工为研究对象，将刀刃在以坐标原点所建立坐标系下的数学表达式分别转化到大轮坐标系和小轮坐标系，推导出齿面方程，编写MATLAB程序求解得到齿面点坐标，导入到UG中，先建立单个齿形齿面，再通过后续的布尔运算和阵列等操作从而建立完整的准双曲面齿轮三维模型。由于文章篇幅有限，本文不再详述准双曲面齿轮具体的建模过程，准双曲面齿轮副基本参数见表2。

表2 准双曲面齿轮副主要参数

准双曲面齿轮传动副三维几何模型如图2所示。

图2 准双曲面齿轮三维几何模型

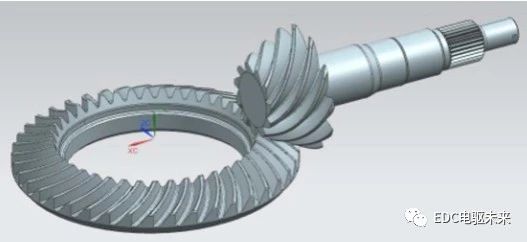
最终得到主减速器主从动齿轮和差速器齿轮的无干涉装配模型，如图3所示。

图3 主减速器和差速器的无干涉装配模型

2 虚拟样机模型的建立

2.1 齿轮接触理论

由Hertz接触理论可知，当齿轮接触碰撞时，齿轮齿与齿之间的法向接触力P和变形δ满足

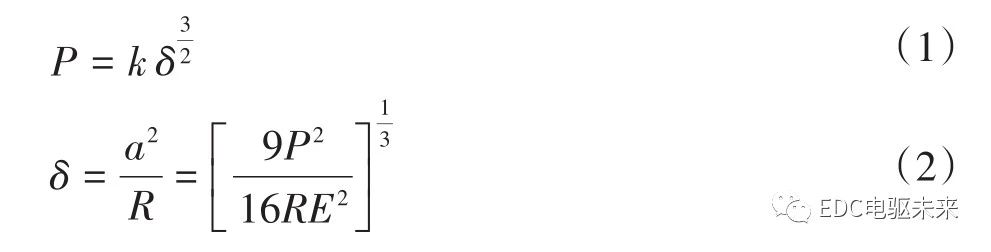
其中，k为刚度系数，。可根据式（1）计算得到准双曲面齿轮齿轮间的接触刚度系数和行星齿轮与半轴齿轮间的接触刚度系数。


式中，E*为当量弹性模量；R为接触点处的当量曲率半径。


在这里，R1、R2分别为两齿轮的节圆直径。


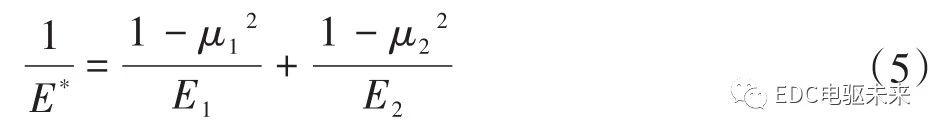
其中，μ1、μ2分别为两物体的泊松比；E1、E2分别为两物体的弹性模量。

2.2 约束和载荷的施加

根据主减速器和差速器的工作原理和工作形式，对虚拟样机模型，模型施加如下载荷和约束：

（1）由于主减速器从动齿轮和差速器壳体是连接在一起的，但差速器壳体与本文研究内容关系不大，所以简化掉了差速器壳体，在主减速器从动锥齿轮和十字轴之间添加固定副；主减速器主从动锥齿轮和2个半轴齿轮分别绕各自的轴线旋转，添加相对于大地的旋转副；4个行星齿轮分别相对于十字轴旋转，各自施加相对于十字轴旋转副。

（2）在主减速器主从动锥齿轮，2个半轴齿轮和4个行星齿轮之间施加接触力，总共添加了9个接触力。

（3）在主减速器主动齿轮上施加转速驱动，根据具体工况分别在半轴齿轮上施加负载转矩。

最终创建的虚拟样机模型如图4所示。

图4 驱动桥齿轮传动系统虚拟样机模型

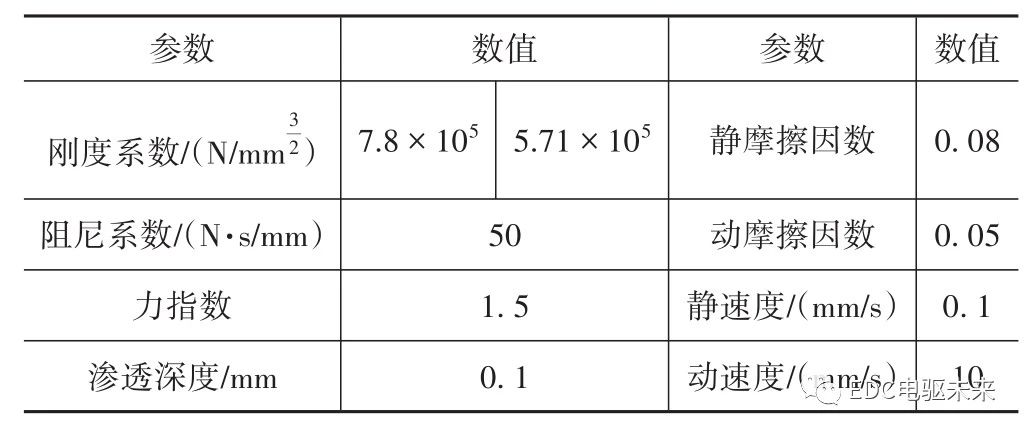
2.3 接触参数的确定
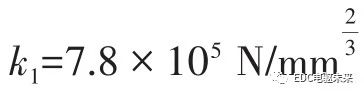接触系数的选取参考了文献[8]，选择齿轮材料为22CrMoH，弹性模量2.07×1011N/m2，泊松比0.29，由式（3）可得准双曲面齿轮齿轮间的接触刚度系数为，行星齿轮和半轴齿轮间的接触刚度为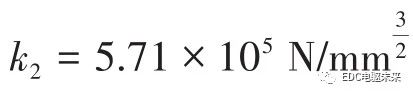，具体接触参数见表3。

表3 接触参数表


3 仿真分析

3.1 起步工况

以某款观光车为研究对象，整车部分性能指标见表4。

表4 整车部分性能指标

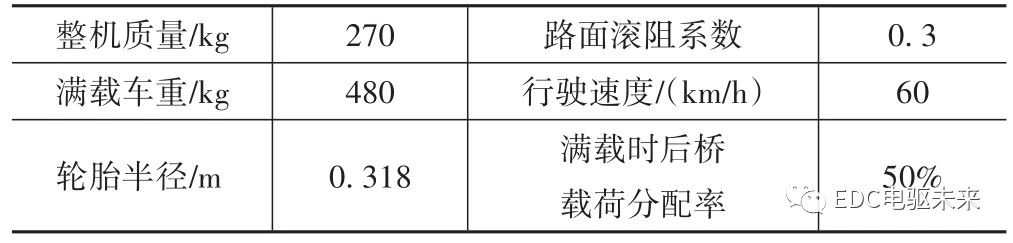
计算可得半轴负载转矩为T=1.12×105N·mm，假设车辆启动加速至10 km/h，每个后轮除受到滚动阻力距外，还受到了加速阻力距，阻力矩值为2.12×105N·mm且缓慢降为0。因此设定负载时间历程函数 T=（1.12×105+STEP（time，0，2.12×105，1.2，0））N·mm，输入端STEP函数为STEP（time，0，0，1.2，2 586d）。设定仿真时间为1.5 s，仿真步长0.001，开始进行仿真。

3.1.1 运动学分析

后处理得到的运动学图像如图5～图9所示。

图5 主减速器主动齿轮输入转速

图6 主减速器从动锥齿轮转速

图7 从动锥齿轮角加速度

图8 行星齿轮转速

图9 半轴齿轮转速

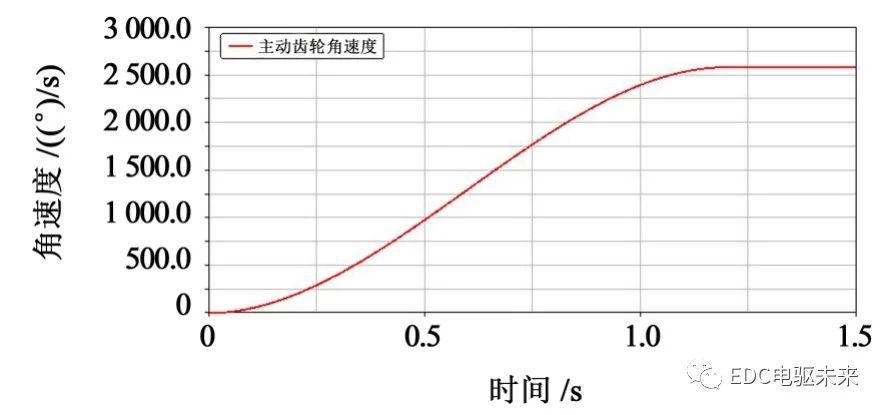
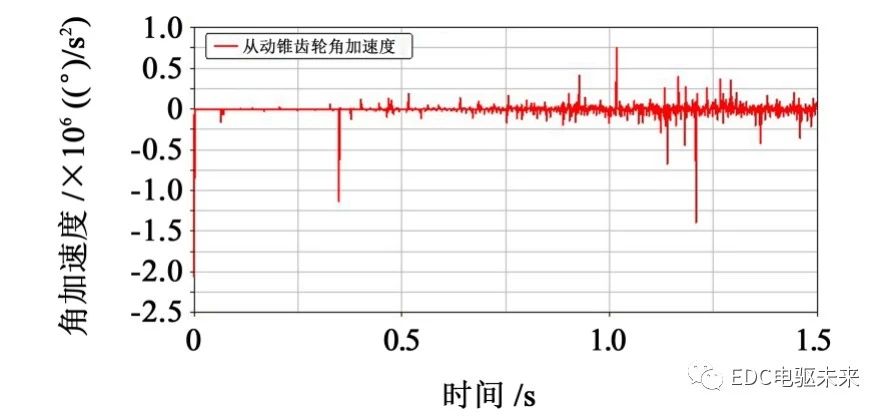
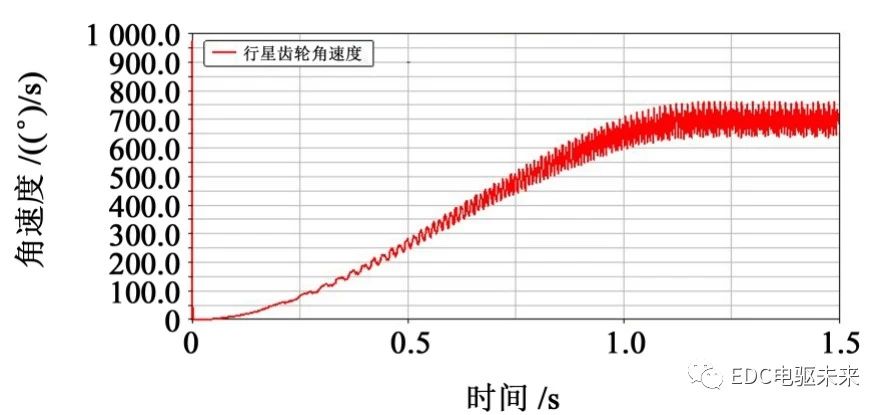
起步初速度为0时，起始处出现由于齿轮刚进入啮合冲击力较大，而引起的转速和角加速度峰值。随着速度达到稳定车速，角速度和角加速度的振动幅度和频率都随之增加，主减速器从动齿轮角加速度总体上做周期性变化，但峰值处出现较大的偏差，出现剧烈波动。行星齿轮和半轴齿轮的速度在1.2 s之前稳步增加，在1.2 s后都趋于周期性的稳定变化，稳定于700(°)/s。

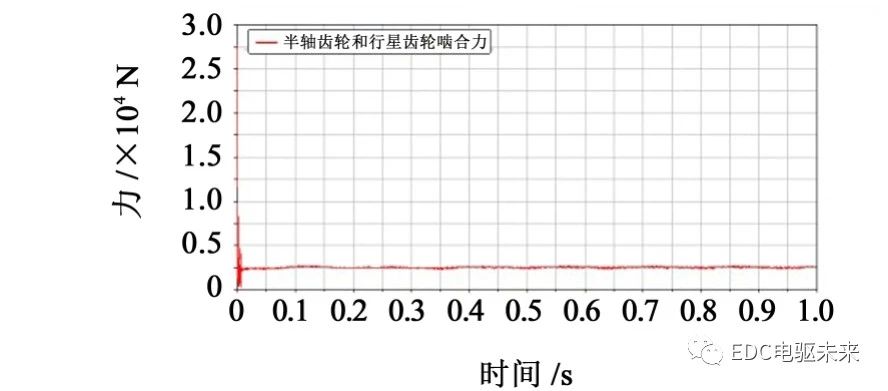
3.1.2 齿轮啮合力分析

起始处出现由齿轮刚进入啮合冲击力较大引起的峰值。在速度达到稳定后，随着加速阻力矩的减小，速度和齿轮间的啮合冲击力随之增大，反映到曲线上就是力的幅值增大。由由图10～图12可以看出：主减速器主从动锥齿轮间的啮合力总体呈现下降趋势，主减速器主从动锥齿轮啮合力趋于2×105N，呈现周期性稳定变化，半轴齿轮和行星齿轮间的啮合力平缓减小，半轴齿轮和行星齿轮啮合力周期性稳定的趋于2.6×105N。

图10 负载转矩图

图11 半轴齿轮和行星齿轮啮合力

图12 主减速器主从动锥齿轮啮合力

3.2 直线工况

直线行驶工况时，差速器不起差速作用，由起动工况可知，在两半轴齿轮施加1.12×105N·mm的转矩驱动，在主减速器主动锥齿轮上添加9 000(°)/s的恒定转速，设定总的仿真时间为1 s，步长为0.001。

3.2.1 运动学分析

由图13～图17可以看出，直线行驶工况时，主减速器和差速器齿轮速度和角加速度总体呈现周期性变化，速度幅值稳定于2 500(°)/s。

图13 主动锥齿轮转速

图14 从动锥齿轮转速

图15 从动锥齿轮加速度

图16 半轴齿轮速度
图17 行星齿轮速度

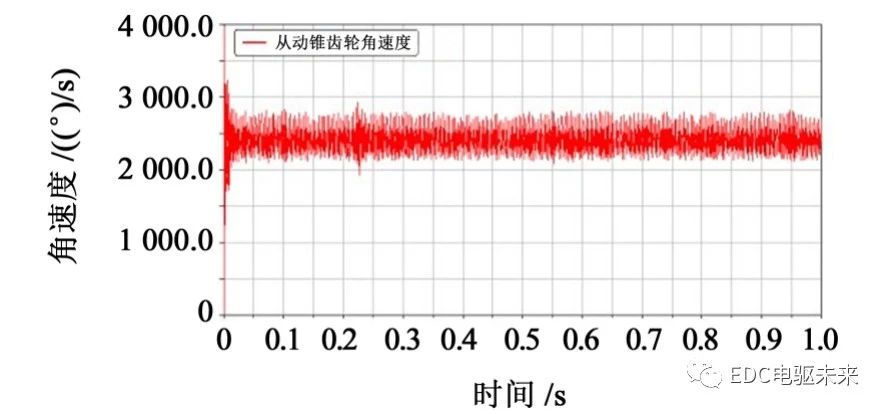
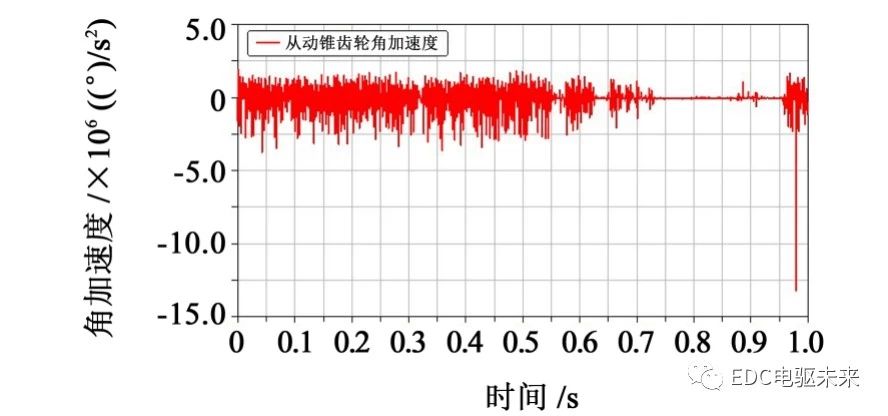
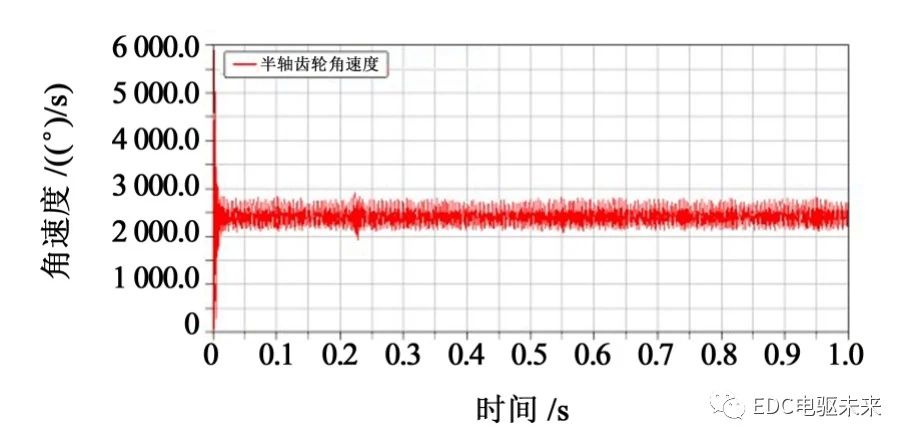
3.2.2 啮合力分析

从图18～图20可以看出，初始状态由于啮合冲击产生峰值突变，但很快趋于稳定，半轴齿轮和行星齿轮啮合力围绕2 500 N上下波动，主从动锥齿轮啮合力周期性稳定于24 000 N，振动的周期及幅度都比较稳定。

图18 半轴齿轮和行星齿轮啮合力

图19 主从动锥齿轮啮合力时域图

图20 主从动锥齿轮啮合力频域图

3.3 转弯行驶工况

转弯行驶时，行驶速度较慢，主减速器主动锥齿轮输入转速取为5 171(°)/s，此时，行星齿轮除承受负载转矩外还受到了附加的摩擦转矩为5 600 N·mm，为了避免过大的突变产生，使驱动缓慢增加，采用的STEP函数为：STEP（time，0.2，0，0.3，5 600）。转弯行驶时，差速器开始起差速作用，差速器行星齿轮转速为200(°)/s，STEP函数为STEP（time，0.2，0，0.3，200d）。仿真时间历程见表5。

表5 仿真时间历程

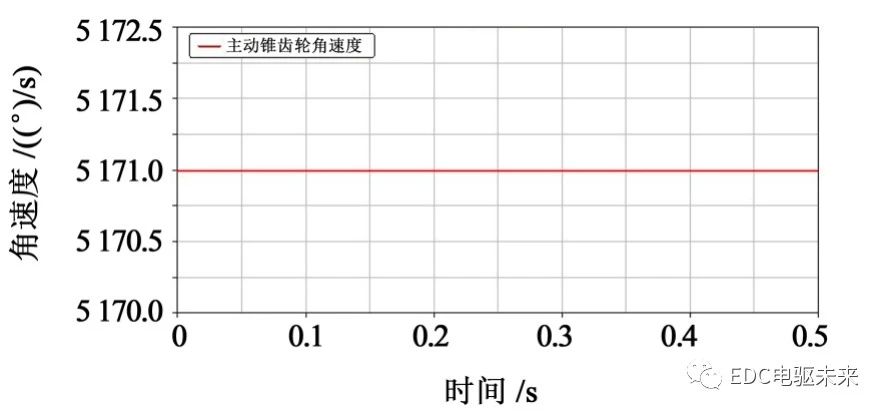
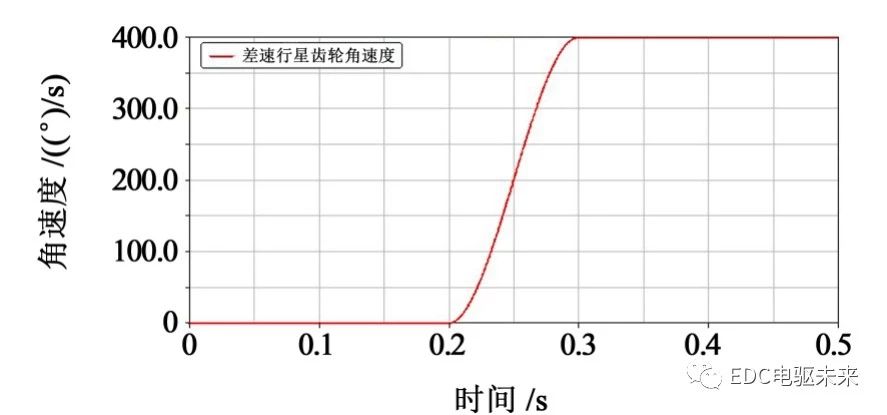
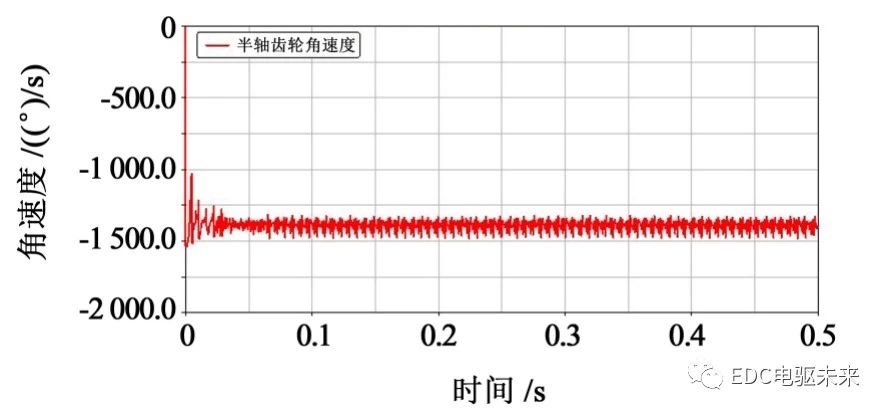
3.3.1 运动学分析

转弯行驶时，差速器发挥差速作用使左右车轮以不同速度转动，由图21～图24可知，左右半轴齿轮的角速度之和约等于主减速器从动锥齿轮角速度的2倍，符合差速器的运动特性，同时也验证了此虚拟样机模型的准确性。
图21 主动锥齿轮转速

图22 差速行星齿轮转速

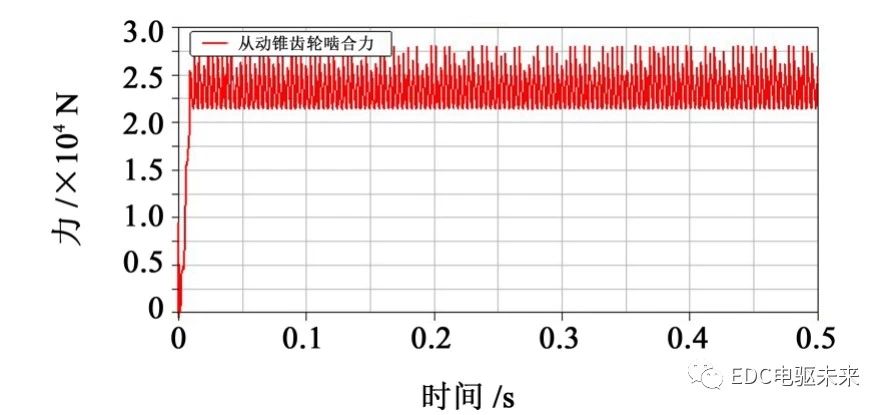
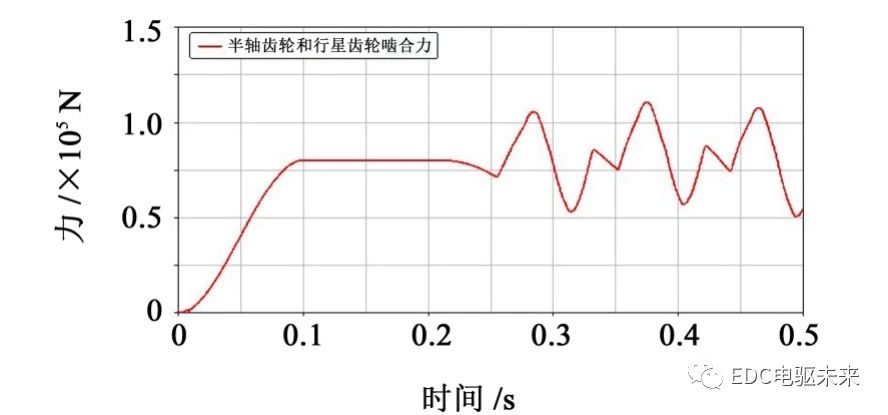
3.3.2 啮合力分析

由图25可以看出，在0～0.1 s，半轴齿轮和行星齿轮啮合力平稳增加至80 000 N，0.1～0.2 s，啮合力很稳定，0.2 s后差速器开始起作用，啮合力呈现周期性变化，这是由此时齿轮的啮入啮出冲击产生的。

图23 从动锥齿轮转速

图24 两半轴齿轮转速对比

图25 半轴齿轮和行星齿轮啮合力

4 结论

（1）完成了驱动桥主减速器主从动锥齿轮、差速器行星齿轮和半轴齿轮的一体化无干涉装配模型的创建，在动力学软件Adams中完成了一体化驱动桥虚拟样机模型构建。

（2）基于Hertz接触理论，结合后桥的实际工况，选取合适的接触参数，施加相应的约束和载荷，进行了齿轮啮合的动态仿真。

（3）运用动力学软件Adams对虚拟样机模型在起动、直线行驶、转弯工况下的运动特性，进行了运动学和动力学仿真，分析了后处理得到的速度、加速度、啮合力曲线图，发现起动工况下啮合力突变和转弯工况下加速度在峰值部分的波动。

（4）根据仿真结果，可以对后桥性能、运动范围、峰值载荷进行预测，并为优化其起动工况和转弯工况的性能特性提供技术支持。
分享到：
 
反对 0 举报 0 收藏 0 评论 0
  • 汽车测试网V课堂

    汽车测试网V课堂

  • 微信公众号

    微信公众号

  • 汽车测试网手机站

    汽车测试网手机站

• 基于VTD的V2X仿真应用 • ODYSSEE 加速电机仿真优化
• 为什么选择BCS？德国comemso倾力打造！！！ • CCS AC/DC欧美标测试分析 | 功能展示篇技术帖（五）
• CCS AC/DC欧美标测试分析 | 功能展示篇技术帖（四） • EVCC | SECC测试分析 | 功能展示篇技术帖（三）
• CANoe EVCA测试分析 | 功能展示篇技术帖（二） • 某电瓶箱箱体开裂问题有限元分析与解决方案
• 电动汽车EV充电桩分析仪测试仪器 | 功能展示篇技术帖（一 • 整车通过性虚拟仿真
0 条相关评论
  • 广告
  • 广告

编辑推荐

最新资讯

  • 广告
  • 广告
沪ICP备11026917号-25