广告
集中驱动式电动车动力总成系统振动特性分析
2019-08-11 19:22:04· 来源：EDC电驱未来
对于集中式驱动电动汽车动力总成，将减/差速器和电机分开进行研究并不能很好地贴合整车试验结果，忽略切向电磁力波也无法全面反映真实的振动噪声特性。将减/差速
对于集中式驱动电动汽车动力总成，将减/差速器和电机分开进行研究并不能很好地贴合整车试验结果，忽略切向电磁力波也无法全面反映真实的振动噪声特性 。 将减/差速器和电机考虑为整体，建立某集中驱动式电动车动力总成系统耦合分析模型，综合考虑轮齿传动系统激励(啮合时变刚度、齿轮传递误差以及齿轮冲击)和电机电磁激励(径向电磁力波和切向电磁力波)的影响，进行动力总成箱体在多源动态激励下的动态响应仿真和消声室整车试验，进一步揭示动力总成系统振动特性，为后续电机动力总成振动噪声性能优化奠定基础。
1 电机动力总成系统
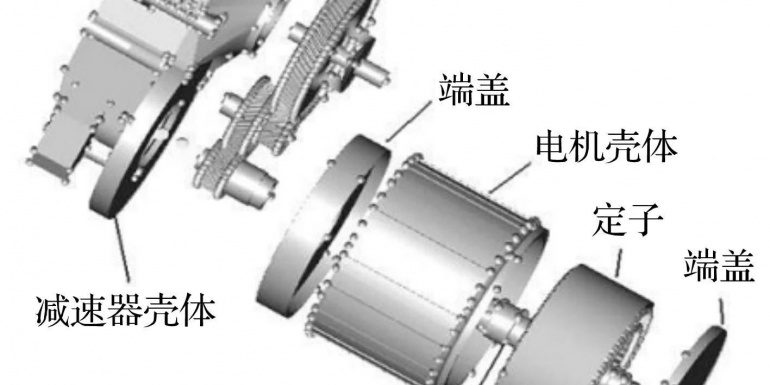
利用 Catia软件建立动力总成各零部件三维实体模型，并按照实际装配关系进行装配，得到如图1所示动力总成实体几何模型 。
图1 动力总成三维实体模型
Fig.1 3D solid model of powertrain
2 齿轮传动系内部激励计算
2.1 齿轮啮合动力学方程
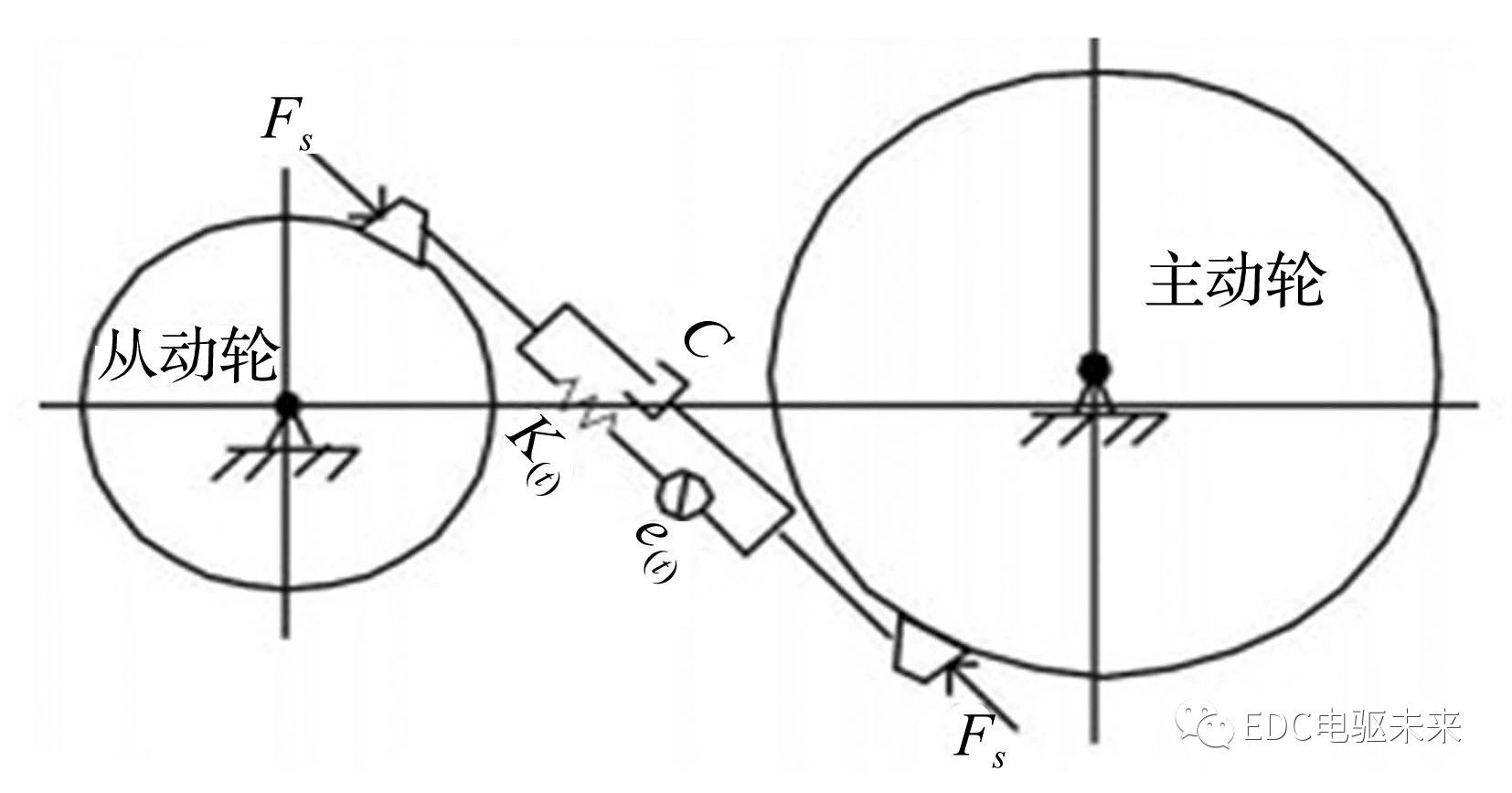
齿轮传动系统通常可简化为图2所示的振动系统 ，其非线性动力学方程可表示为。
图2 齿轮系统振动模型
Fig.2 Gear system vibration model
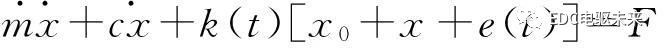
(1)
式中:m为齿轮副等效质量；c为系统阻尼系数；k(t)为齿轮啮合刚度；x 0为啮合齿轮静态相对位移；
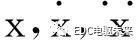分别为振动位移、速度和加速度；e(t)为齿轮综合误差，包括齿形误差和基节误差；F为外部载荷。令k(t)=k 0+ k A( t)
式中：k 0为齿轮啮合刚度常值； k A( t)为时变刚度部分。
上式可化为：
(2)
式(2)右端激励可看作齿轮啮合刚度变化部分与齿轮综合误差的乘积，则齿轮啮合激励可表示为：
F(t)=k A( t) e( t)
(3)
2.2 齿轮啮合时变刚度
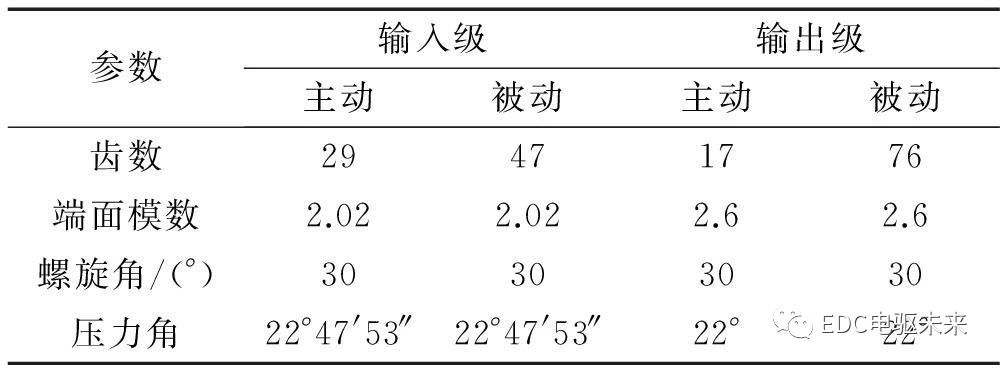
齿轮啮合过程中，参与啮合的轮齿对数会做周期性变化，同时轮齿在从齿顶到齿根的啮合过程中，弹性变形也不断变化，这些因素导致齿轮啮合刚度变化。所研究齿轮传动系的参数如表1所示。
表1 齿轮传动系参数
Tab.1 Parameters of gear transmission system
对于宽齿斜齿轮副，当单位接触线长度的啮合刚度为常数k 0时，其时变啮合刚度可以用时变齿轮副接触长度 L( τ) 来表示
k(t)=k 0· L( τ)
(4)
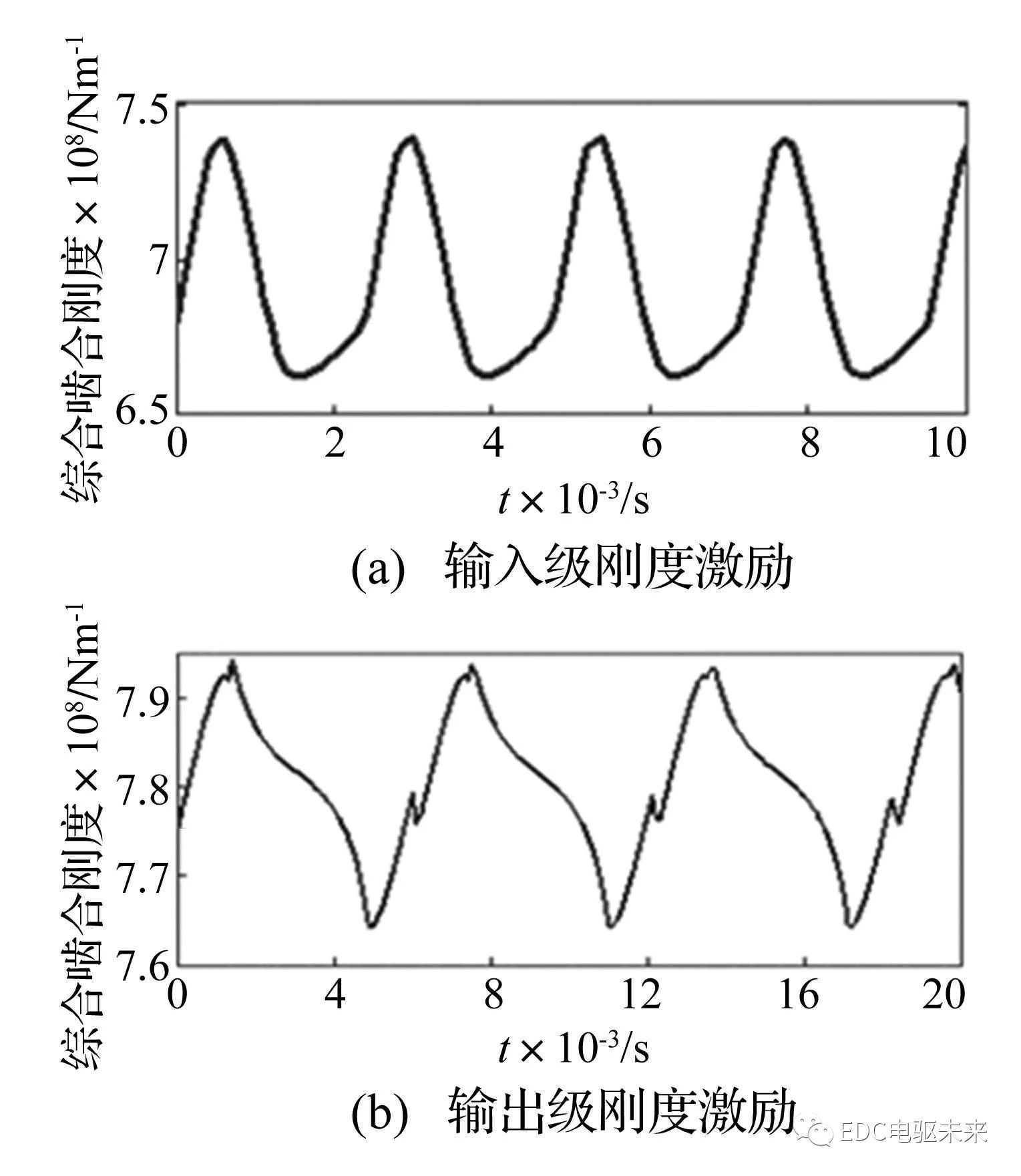
编程得到输入级、输出级齿轮的考虑时变啮合刚度的综合啮合刚度曲线，如图3所示。
图3 综合啮合刚度曲线
Fig.3 Integrated mesh stiffness curve
2.3 齿轮误差激励
由于齿轮加工误差和安装误差使得齿轮啮合齿廓偏离理论的理想位置而引起齿轮瞬时传动比发生变化，使齿轮啮合时发生碰撞与冲击，从而产生齿轮啮合误差激励。根据齿轮设计的精度等级确定齿轮的偏差,采用简谐函数模拟这种误差，则轮齿误差可用正弦函数表示为:
e( t)= e 0+e r sin(ωt/T+φ)
(5)
式中：e 0、e r分别为轮齿误差常值和幅值，通常取e 0=0，T为齿轮啮合周期，ω为主动齿轮转速，φ为相位角，e r由齿轮的精度等级而定。编程可得到该误差激励，为具有一定幅值和相位的正弦波。
2.4 齿轮冲击激励
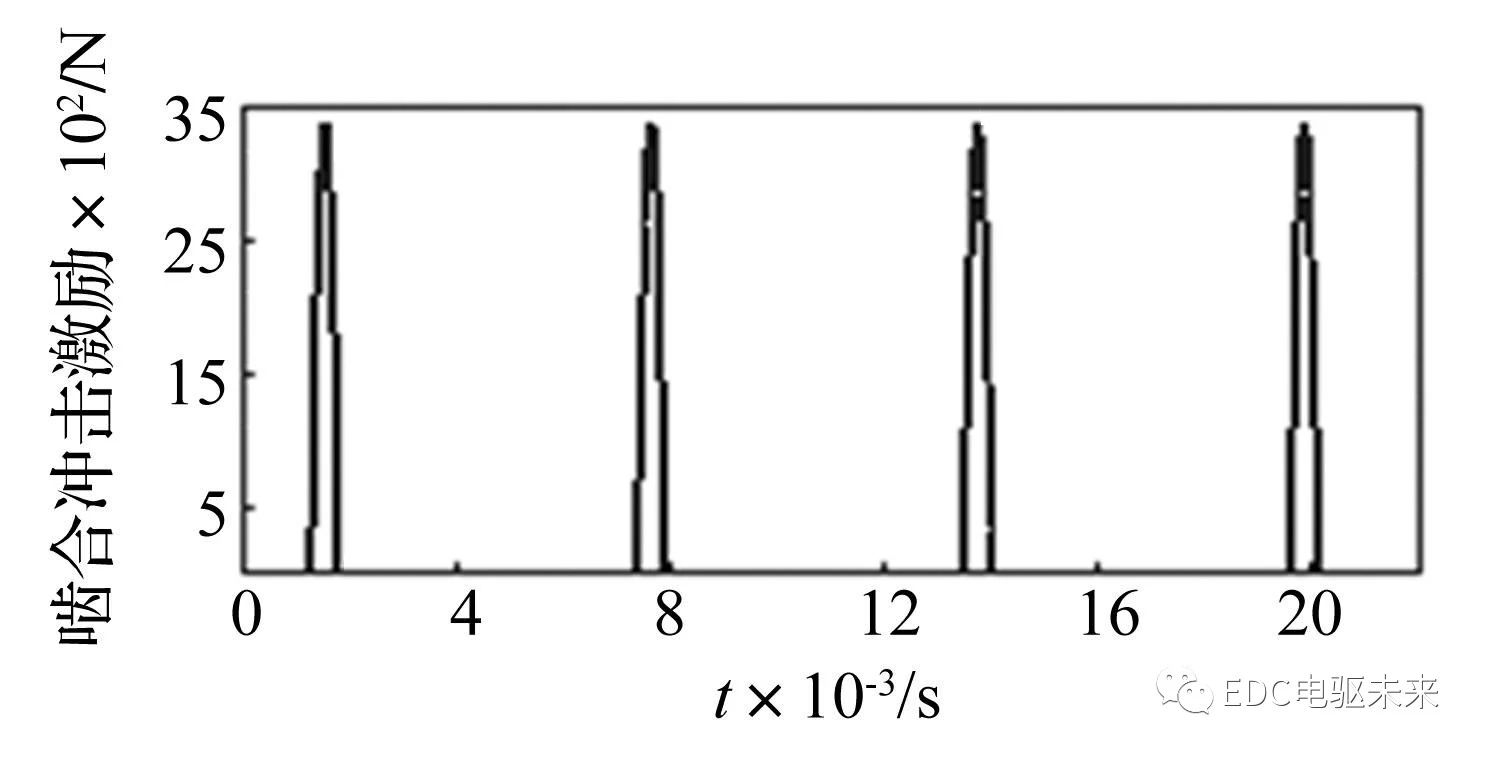
轮齿在进入啮合时，由于齿轮误差和受载弹性变形，其啮入点偏离啮合线上的理论啮入点，将引起啮入冲击；在轮齿退出啮合时，同样会产生啮出冲击；这两种冲击激励统称为啮合冲击激励。考虑到啮入冲击的影响比啮出冲击大，仿真中只计入啮入冲击的影响。可参考文献 [15 ]编程计算齿轮传动系输入、输出级啮合冲击力，某级冲击激励曲线如图4所示。
图4 齿轮啮合冲击
Fig.4 Gear mesh shock
3 电机电磁激励计算
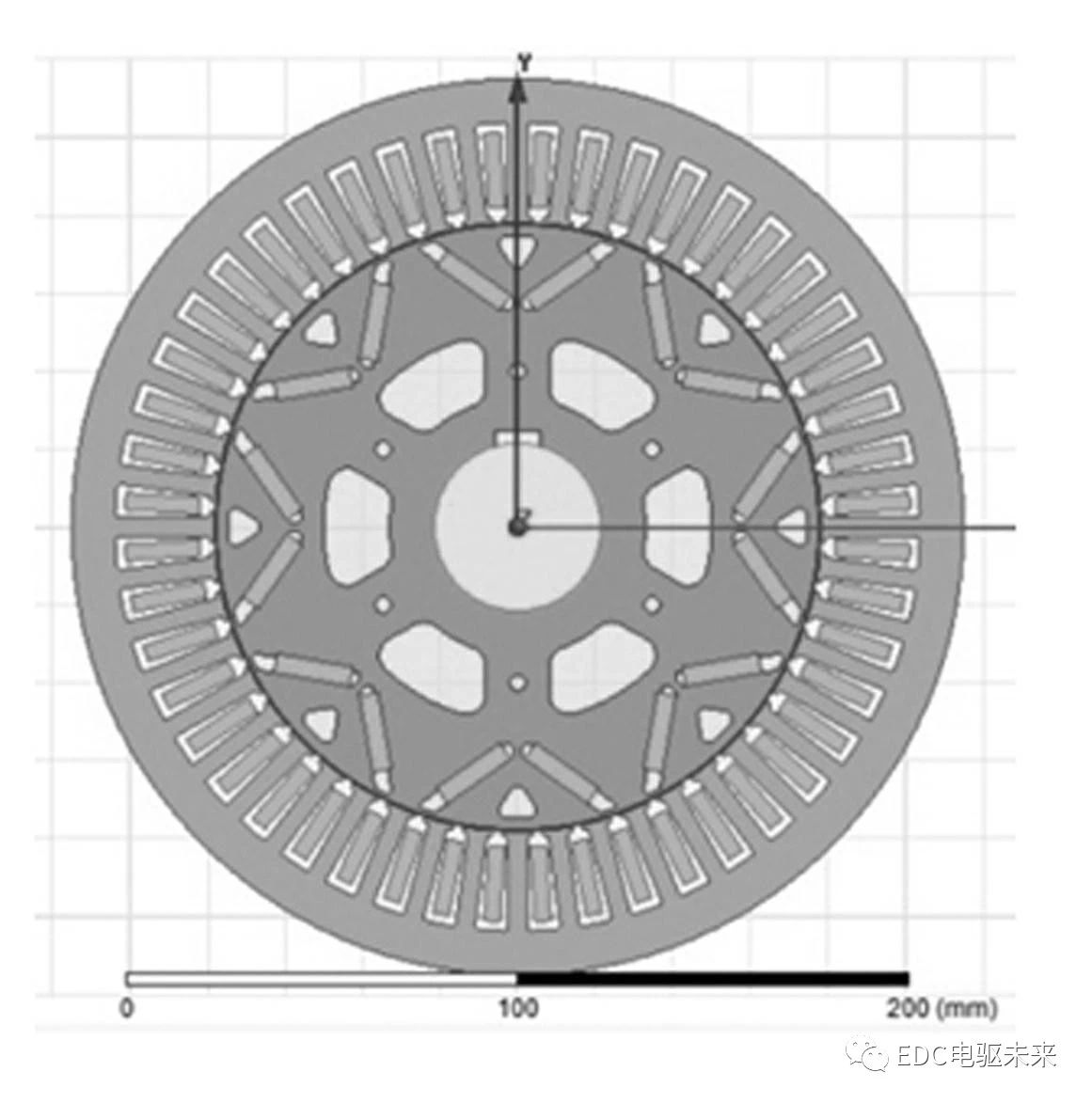
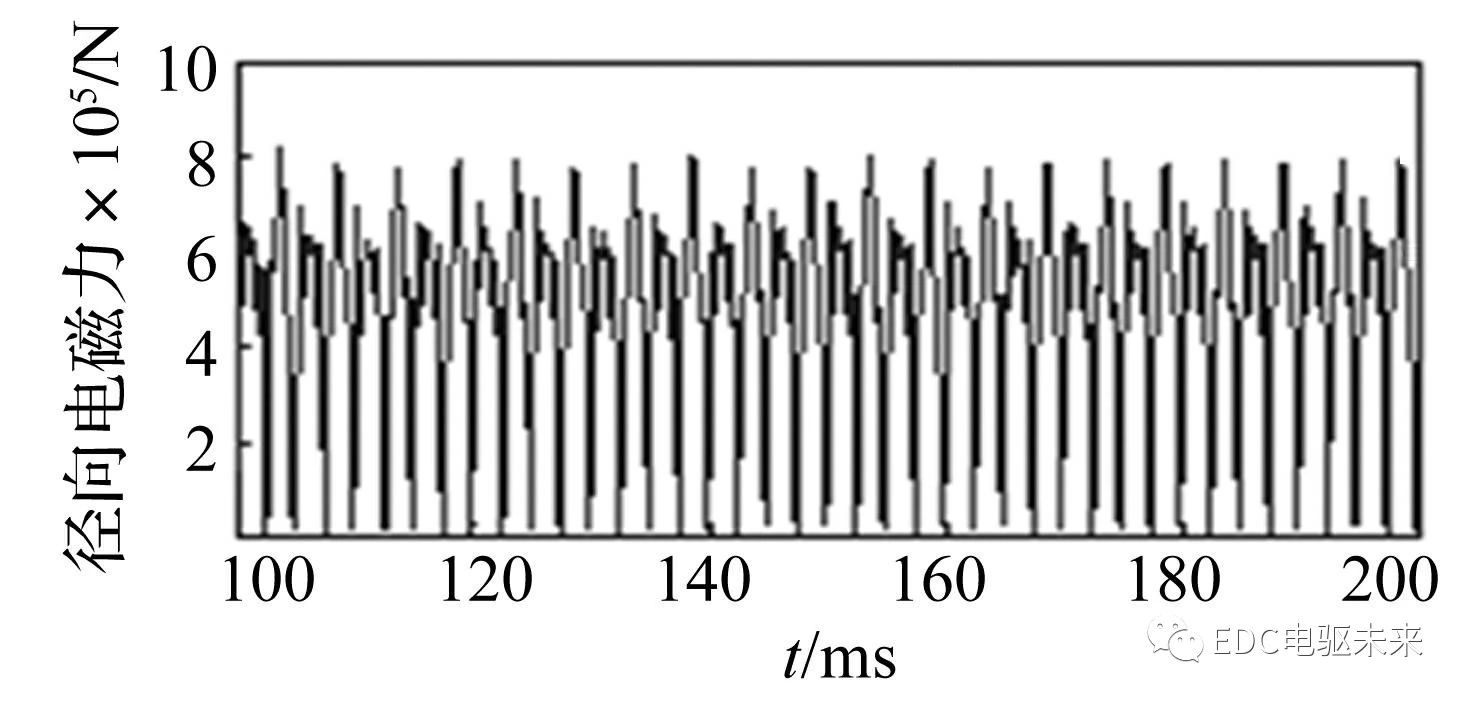
所研究电动车的驱动电机是45 kw永磁同步电机。使用有限元软件 Ansoft/ Maxwell，搭建二维有限元电磁分析模型，如图5所示。基于 Maxwell电磁理论可计算转子在任意转速下的径向电磁力波和切向电磁力波，电磁力波的理论计算及仿真结果可参见文献 [12 ]，仅以电机转子3 000 r/ min为例，给出电磁力波仿真结果如图6、图7所示。
图5 电机有限元电磁仿真模型
Fig.5 Finite element electromagnetic
simulation model of the motor
图6 定子齿槽某点径向电磁力波
Fig.6 Stator alveolar radial electromagnetic force at one point
图7 定子齿槽某点切向电磁力波
Fig.7 Stator alveolar tangential electromagnetic force at one point
4 动力总成振动特性仿真
4.1 动力总成有限元模型
根据模型的几何特征、分析类型和精度要求,对体部分采用四面体和六面体单元, 薄壳部分采用壳单元, 体单元与壳单元通过共节点连接。考虑动力总成内部齿轮传动系统的影响，通过 Rigids单元与壳体相连接来模拟轴与轴承的接触, 最后得到的动力总成有限元模型外观如图8所示。为验证该动力总成模型的正确性，分别进行了减/差速器部件、电机部件、动力总成组件的模态仿真分析和模态试验验证，具体可参见文献 [11，14 ]。
图8 动力总成有限元模型
Fig.8 Finite element model of the powertrain
4.2 动力总成系统动态响应分析
在整车状态下，动力总成通过悬置系统连接在副车架上，但是悬置系统的模态频率域较低(为30 Hz~90 Hz，表2所示为动力总成悬置系统模态试验结果)，不影响高频振动及噪声的测量结果，因此在进行动态分析时，约束悬置安装处的各向自由度；添加激励时，将前面计算得到的齿轮啮合动载荷和电磁力作为综合激励，分别施加于动力总成轴承处和电机定子齿处，进行动力总成在综合激励下的动态响应分析。在后处理模块中可提取减速器和电机表面振动加速度结果，为便于分析，将振动加速度时域结果进行快速傅里叶变换，得到频域结果如图9、图10所示。
从图9看出，减速器 X向加速度在1 250 Hz、2 526 Hz、3 333 Hz、3 815 Hz出现峰值，而1 250 Hz、2 526 Hz和3 815 Hz分别是齿轮啮合频率的一倍频、二倍频和三倍频，说明这三处峰值是由齿轮啮合激励引起，而3 333 Hz则可能是由电机的电磁力波激励引起，若不考虑电磁力波激励并且不使用动力总成整体模型进行仿真则无法获得该频率。
表2 整车状态下动力总成悬置系统模态试验结果
Tab.2 modal test result of powertrain mounting
system under whole vehicle situation
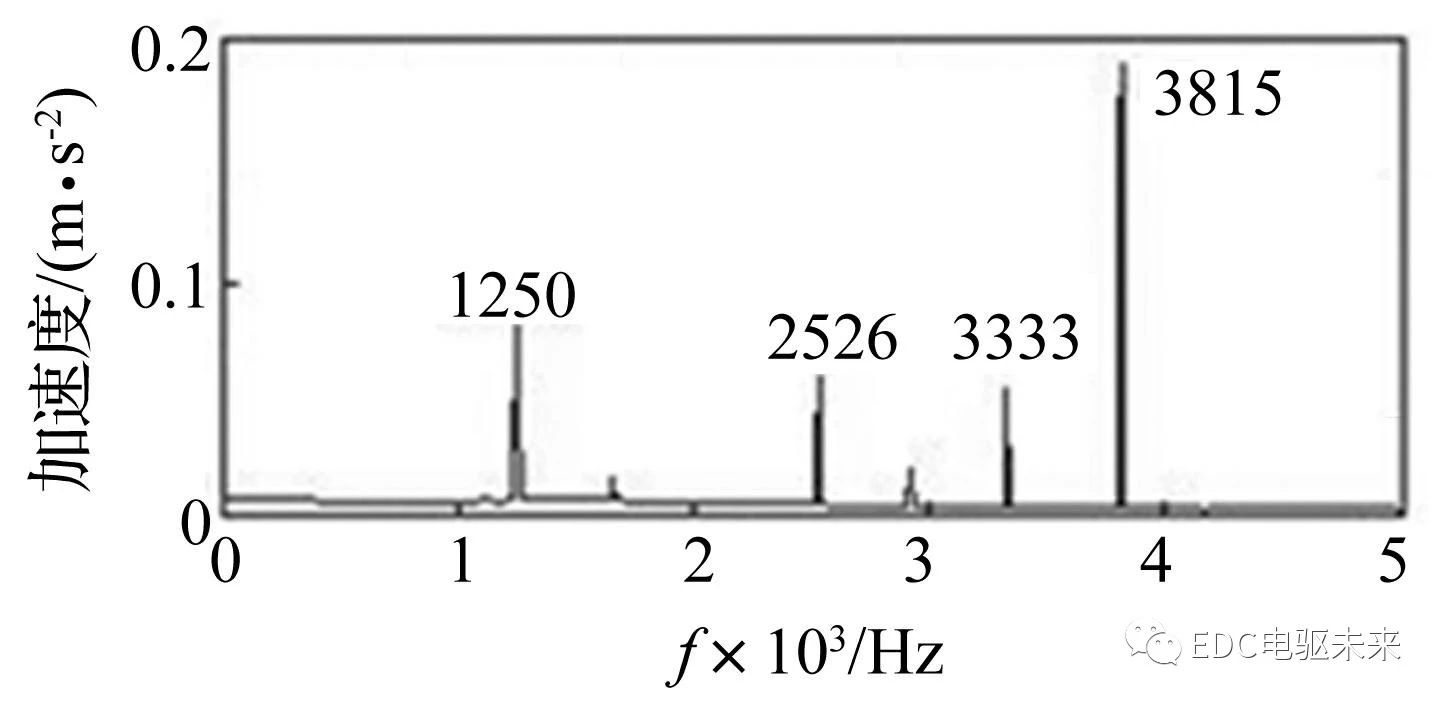
图9 减速器表面某点X向加速度频域曲线
Fig.9 X-direction acceleration on
Reducer surface under frequency domain
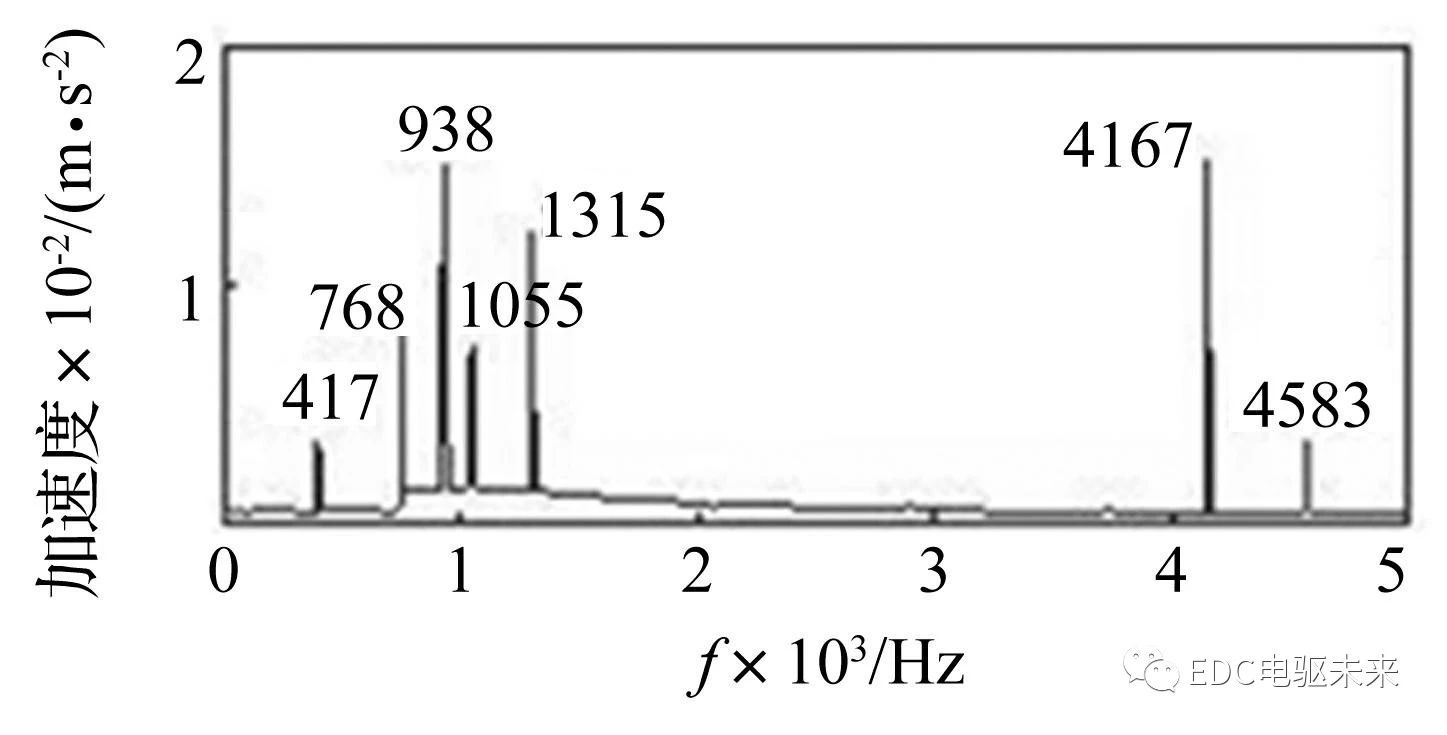
图10 电机表面某点X向加速度频域曲线
Fig.10 X-direction acceleration
on motor surface under frequency domain
图11 动力总成表面速度分布
Fig.11 Velocity distribution of Powertrain surface
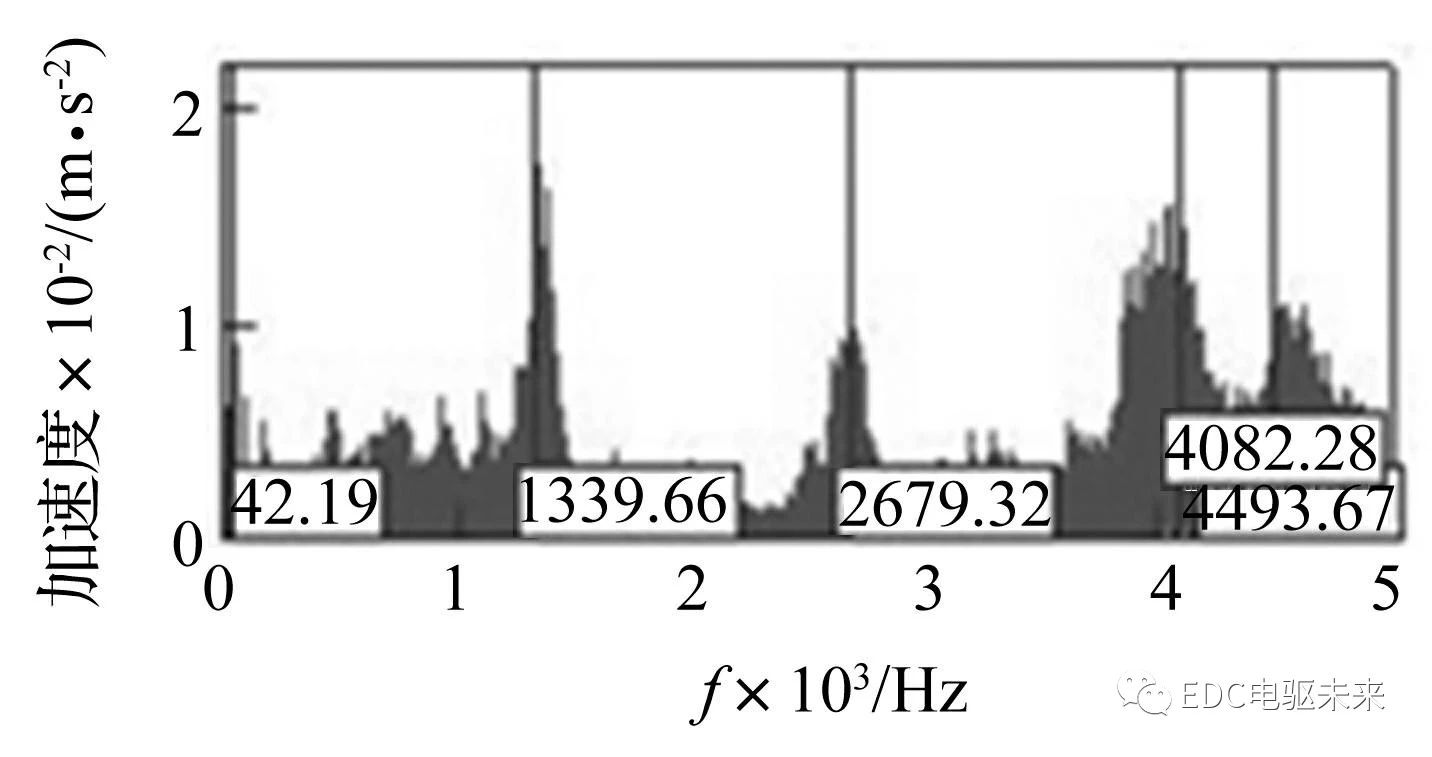
从图10 可看出，在电机外侧X向加速度峰值频率中，417 Hz、768 Hz、1 315 Hz、4 167 Hz、4 580 Hz是由电机径向电磁力波引起，对应的电磁力波激励频率为400 Hz、800 Hz、1 200 Hz、4 000 Hz、4 580 Hz，这些激励频率引发了总成壳体与其相近频率点的模态共振 。而938 Hz、1 055 Hz则可能是由于切向电磁力波激励和齿轮激励综合作用的结果，若不考虑切向电磁力波激励和齿轮激励，并且不使用动力总成整体模型进行仿真也无法获得此二频率。
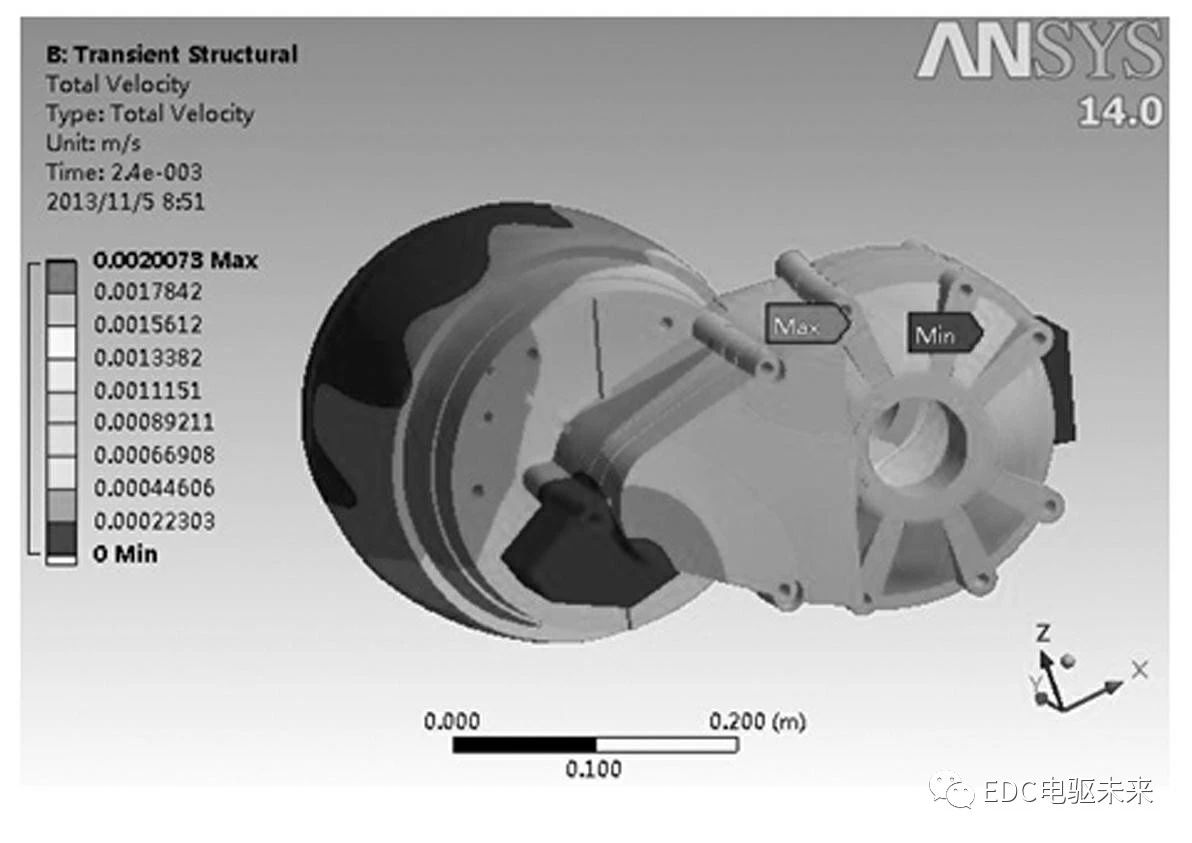
为整体把握动力总成的振动情况，奠定后续基于动响应进行箱体优化的基础，可以查看任意时刻动力总成表面加速度和速度的分布情况，如图11所示为动力总成表面速度分布情况。由图可知差速器部分轴承座附近壳体的加速度值和速度均较大，是后续优化的重点，暂不涉及动力学优化的内容。
5 整车振动试验
为验证仿真结果的正确性，在半消声室内，转鼓试验台上进行整车状态下的振动噪声试验。图12所示为试验现场图，其中车辆即为所研究的集中式驱动纯电动车，在举升机上贴好加速度传感器，将车辆固定在转鼓试验台上，然后对应传感器位置布置麦克风。由驾驶员操作车辆，使用 LMS数采系统记录不同工况下的振动噪声数据，用于后续处理分析。试验主要测量动力总成箱体表面的振动加速度、噪声信号、电机转速以及转矩信号。图13所示为某一加速度传感器及对应位置的麦克风布置图。
图12 消声室振动试验
Fig.12 Vibration test in Anechoic chamber
图13 传感器和麦克风布置图
Fig.13 Layout of sensor and microphone
将图14的试验结果与图9的仿真结果对比可知，除仿真中1250 Hz的频率峰值未在试验中测得外，其余的三个峰值频率2 526 Hz、3 333 Hz、3 815 Hz均在试验中被反映了出来。同时从试验结果可知，在3 000 Hz到4 500 Hz的频域内，减速器表面具有较密集的峰值，这与动力总成第七阶次到第十阶次的固有模态频率均分布在此频率范围内相一致。
图14 减速器表面X向加速度频谱曲线
Fig.14 X-direction acceleration on
Reducer surface under frequency domain
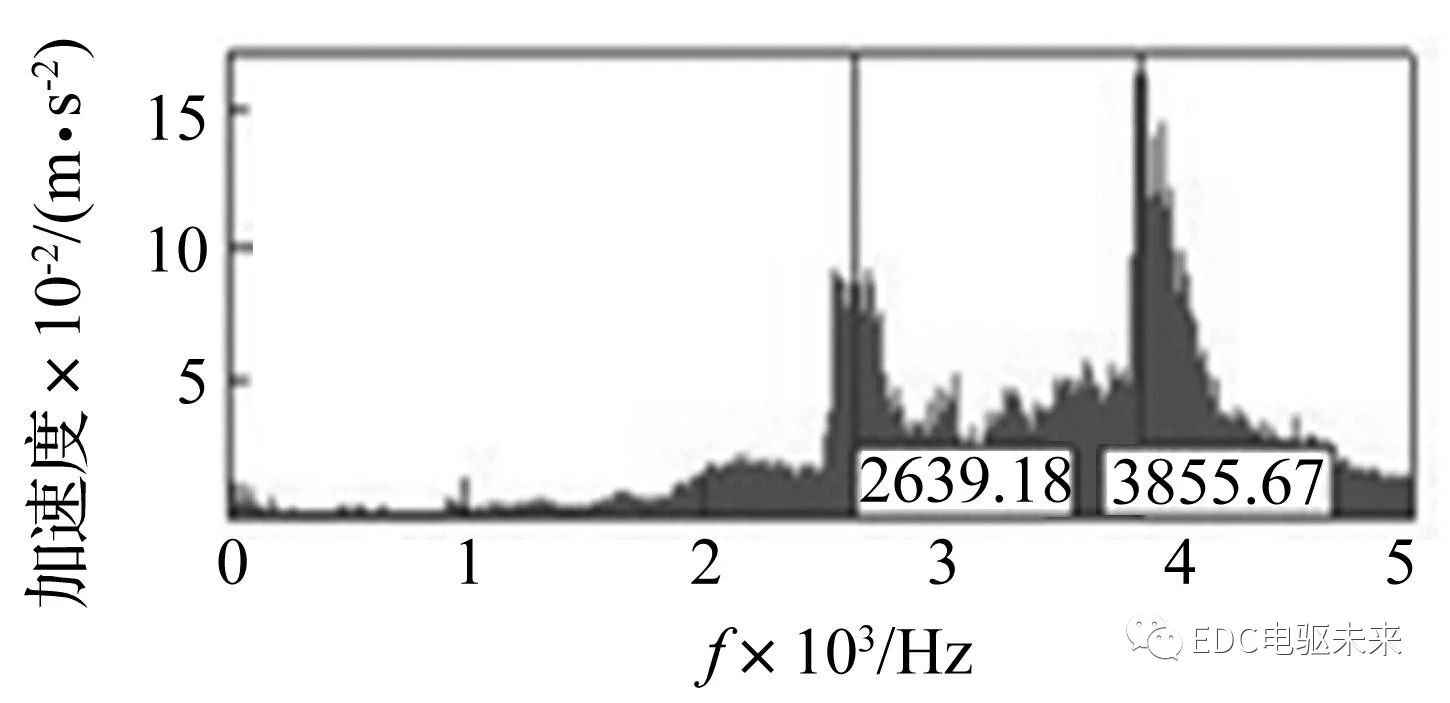
将图15的试验结果与图10的仿真结果对比可知，除试验中2 679.32 Hz对应的峰值外，仿真结果基本反映了试验中较为显著的峰值，而且频率值对应的也较好，证明仿真结果的正确性。对于减速器表面和电机表面均测得的2 650 Hz附近的峰值，原因是齿轮综合激励引发了总成第六阶模态(第六阶固有频率值为2 655 Hz)共振。在电机表面振动仿真结果中未获得该频率，说明仿真模型和激励的添加仍有改进空间。但是，总体来看试验结果和仿真结果中各个测点加速度的主要频率及其幅值均具有较强的一致性，说明考虑综合激励、建立总成整体模型这一仿真方法可以较好的预测主要激励源对动力总成振动特性的影响。
图15 电机表面X向加速度频谱曲线
Fig.15 X-direction acceleration on
motor surface under frequency domain
6 结 论
(1)将电机和减速器视为整体，建立动力总成整体模型，从而进行的仿真研究与单纯对电机壳体或者减速器箱体进行仿真研究相比，更能反映动力总成的振动噪声特性。
(2)综合考虑机械传动部件的激励和各向电磁激励，与单纯考虑径向电磁力波相比，能得到更好的仿真结果，与试验结果吻合的较好。
(3)将动力总成视为整体、综合考虑机械激励和电磁激励的仿真方法虽取得了较好的效果，但是仍有个别频率的峰值未给予很好解释，应该继续进行总成模型的细化、激励的更准确模拟和添加、轴系柔性及支撑柔性的考虑等工作，以使该仿真方法能更好的预测电动车动力总成的振动及噪声特性。
广告 
广告
编辑推荐
最新资讯
-
《rFpro汽车仿真测试应用系列：智能大灯测
2024-12-04 15:38
-
2025年HBK线下培训课程计划
2024-12-04 11:46
-
欧盟委员会拨款46亿欧元，推动净零技术、电
2024-12-04 11:45
-
曼恩能源解决方案，全尺寸二冲程氨发动机开
2024-12-04 11:44
-
大众汽车“主动弹出式引擎盖”技术
2024-12-04 11:42
广告
广告
