广告
纯电动汽车永磁同步电机矢量控制仿真研究
2019-09-04 10:15:20· 来源：汽车技术研究所
电机对于EV 的作用如同人体的心脏一般，所以驱动电机的选择显得尤为重要。永磁同步电机以其优越的可控性和可靠性足以满足电动汽车多工况运行条件，成为电动汽车
电机对于EV 的作用如同人体的心脏一般，所以驱动电机的选择显得尤为重要。永磁同步电机以其优越的可控性和可靠性足以满足电动汽车多工况运行条件，成为电动汽车中应用广泛的驱动电机。PMSM 控制系统的高精准度要求成为现代工业各个领域亟待解决的问题，由于空间矢量脉宽调制控制方式有诸多优点，如调速区间大、高次谐波少、容易公式化等，SVPWM 方法成为PMSM 控制的常客。磁链追踪是SVPWM 方法的基本思想，简单来说，就是将电源转换器和PMSM 视为一体，再由IGBT 的6 个通路开关信号的交叠产生8 个初始电压空间矢量，这8 个初始矢量再合成实际的电压空间矢量，从而使合成矢量的转动路径最大程度上形似圆形的基本磁链圆。一般来说，高性能PMSM 矢量控制系统需要达到高精准要求，因此在 Matlab/Simulink 软件中搭建关于SVPWM 的永磁同步电动机的仿真模型是必不可少的。本文讲述了PMSM 的数学建模方法，对空间矢量控制方法进行了简单的梳理，用模型图形象展示了经典速度、电流双闭环控制系统原理，并对 Matlab/Simulink 得到的结果图进行分析，证明了该仿真实验的实用性。
1 永磁同步电机数学模型
由于永磁同步电机的数学模型变量多，参数时变，且逻辑复杂，因此，为其设计合理的控制算法，建立合适的数学模型成为行业内的重要任务。首先，简化模型，假定PMSM为理想对象，且符合如下要求：
（1）忽略电机铁芯的饱和。
（2）不考虑电机中的磁滞损耗和涡流效应。
式中：T 为周期，T60，T120 分别为电压矢量U60，U120 的作用时间，T0 为零矢量作用时间。将Uref 分解为Uα、Uβ 空间矢量，可得式（7）：
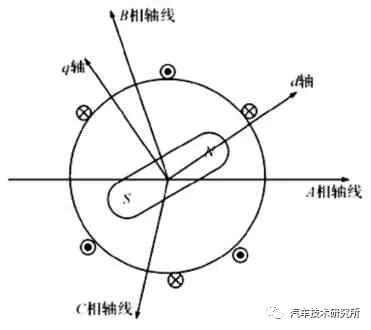
图1 永磁同步电机的物理模型
采用基于d-q 坐标的数学建模方法，是实现PMSM 数学模型解耦的常用方式，这样便于构建PMSM 的数学模型。
为实现坐标置换前后功率的一致性，从定子ABC 三相坐标轴到转子d-q 轴的坐标置换过程中，d-q 轴电流峰值应为定子ABC 坐标系下电流峰值的倍。将定子坐标系下的电压方程变换成d-q 坐标系下的电压方程需要通过一个变换因子实现，变换后的方程如下：
式中参数如下表：
表1 方程各参数
d-q 坐标系中的PMSM 转矩方程为：
式中：是机体永磁体的ψ和Isq 合成的永磁转矩。
以Is 为例，经过3/2 旋转变换可得：
2 矢量控制原理
矢量控制算法是建立在PMSM 的数学模型基础上的控制理论，其主要思想是：通过坐标置换把复杂的交流电机的数学模型转化成直流电机模型，对交流电机耦合的模型进行解耦，然后对其采用直流电机的控制方法，最终经过坐标逆变换回到控制对象本身。
2.1 坐标变换理论
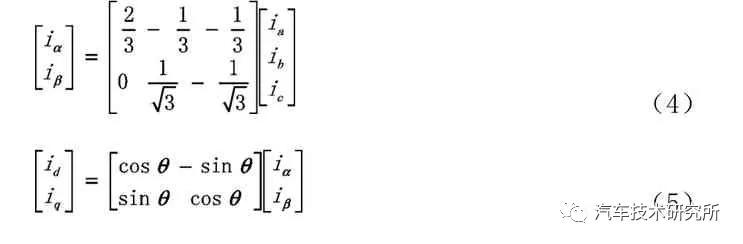
传统矢量控制中，先把三相的a-b-c 坐标转成两相的坐标，此过程称为Clark 变换；再把静止的坐标系转成不断变化的d-q 坐标，此过程称为Park 变换。由于电机采用星形连接且通入的三相电流互差120o。则可得如下等式：
（3）通入电机中的三相绕组电流为对称的三相正弦波电流。
2.2 SVPWM 原理
SVPWM 是以等均值原则为基础的 ，所谓等均值原则，就是在一个上下电平组合中，求电压空间矢量均值，并且将此均值等效为某一电压值。由此以来，该矢量通过转动到对应区域中的零矢量，并且在时域上进行不同的组合得到不同时刻的电压矢量。通过电源转换器的不同开关组合所对应的实时磁通去接近理论磁通圆[6]。
假定某时间内Uref 在第2 个扇形区域，依据伏秒平衡原理：
回到家，老伴早已准备好了晚餐，是典型的中式清淡食谱，两盘青菜一坛菌汤。虽说都是蒋利学可口的，他都几乎没顾上看一眼，便一头扎进书房改起学术报告来。老伴担心他身体吃不消，忙不迭地盛好饭菜端进书房，想劝他趁热赶紧吃一口再赶写学术报告，蒋利学却一点儿也不领情，挥手说：你没看我正忙着吗？
有效电压空间矢量幅值都为Udc，由式（6）和式（7）两式推导可得式（8），由式（8）推导可得式（9）：
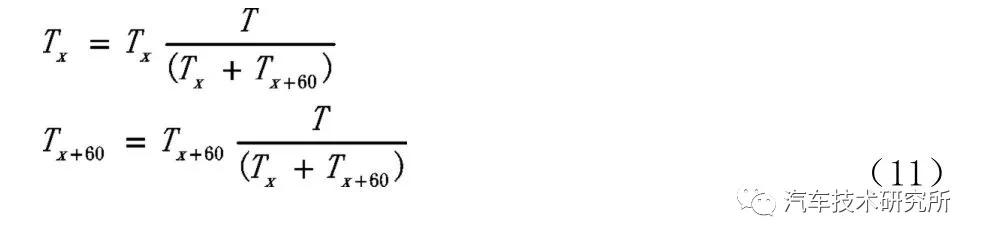
式（9）表明，电源转换器输出相电压最大值是，SPWM相电压最大值是0.5Udc，在相同的直流母线电压下，SVPWM要高出SPWM 大约15%。当参考电压Uref 介于不同扇区时，同理可得邻边电压矢量作用时间，为了较方便的确定时间，定义：
如果相邻电压矢量作用时间TX，TX+60 之和大于周期T，则进行饱和约束：
3 仿真模型的建立
本文利用MatlabR2014b 仿真软件，基于其中的Simulink Common 模块库和SimPowerSystems 库中的模块，搭建PMSM的矢量控制仿真模型。SimPowerSystems 栏里具有电力电子领域各种成型模块，利用其中的电机模块、电源逆变器模块可以大大降低模型搭建的复杂程度。整个模型由多个不同的小模块构成，其中矢量控制模块主要包括坐标变换模块和SVPWM 模块。模型搭建流程如图2 所示。
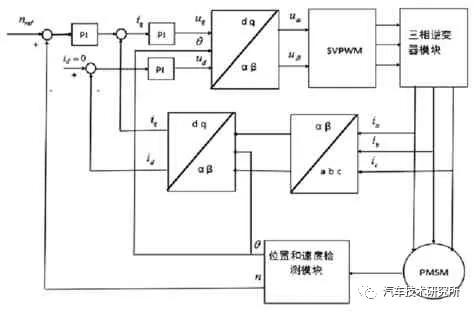
图2 速度、电流双闭环矢量控制系统原理框图
利用id=0 的控制方法，是PMSM 矢量控制的核心。通过对定子侧电流和转子侧转速的监控，来构建电流侧和转速侧的矢量控制系统。矢量控制系统主要是由Is 监控，ωr 监控，Clark、Park 变换及其逆变换、空间矢量脉宽调制等几个模块组成。其中，定子侧的电流由同步电机定子端提供，然后整合到转子侧的旋转坐标下得到一个回馈值，再与实际值进行对比后由电流整流器产生。定子三相电流经过空间矢量脉宽调制得到脉冲驱动逆变器产生三相定子电压输送给PMSM的定子端，达到控制目的。以PMSM 的数学模型及控制框图为基础，搭建出Simulink 模型,如图3、4 所示。
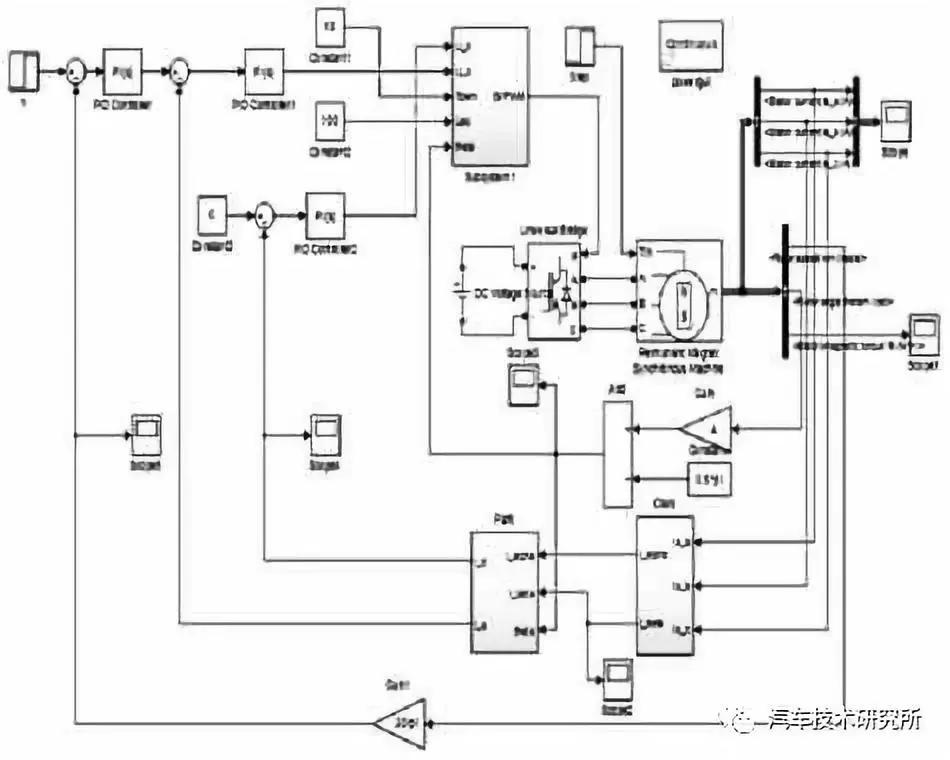
图3 PMSM 矢量控制仿真模型
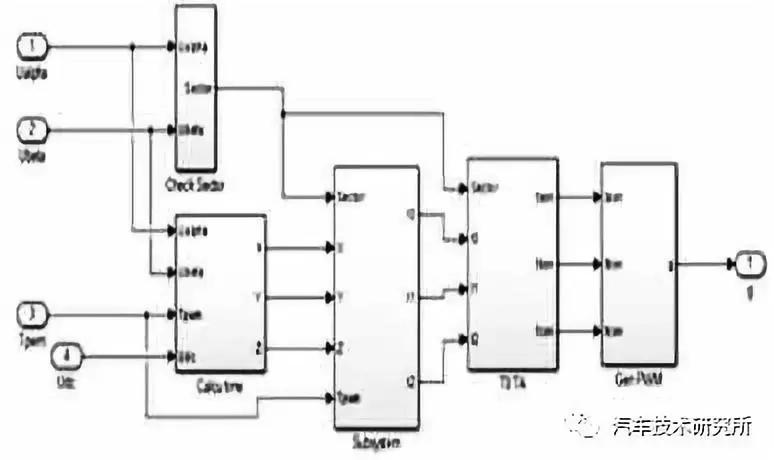
图4 Matlab/Simulink 系统中SVPWM 模型
4 仿真结果分析
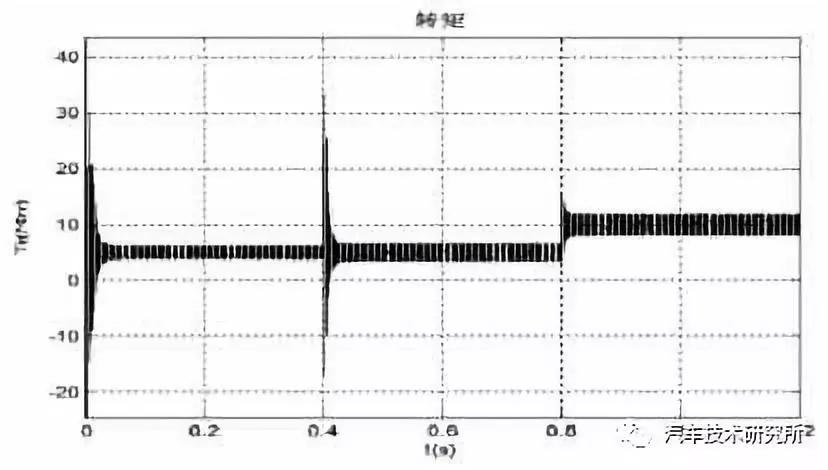
在Matlab/Simulink 中搭建永磁同步电机基于id=0 的矢量控制模型后，进行仿真分析，仿真时需要规定PMSM 的具体参数，本文规定PMSM 的参数如下：定子每相电阻R=2.75，转子直、交轴电感Ld=Lq=0.008H，转子永磁磁链=0.273Wb，转动惯量J=0.000815kg。m2=，Nn=1000rad/min，Tn=4N.m，in=3.3A，极对数p=4。起始给定转速500rad/s，0.4s 时加载到800 rad/s，模拟超车加速工况；起始加转矩5N.m，0.8s时加载到10 N.m，模拟大力矩爬坡工况。仿真时间设置为1.2s。由此仿真获得的的电磁转矩仿真波形图如图5 所示，转子侧转速结果图如图6 所示，定子侧电流结果图如图7 所示。
图5 电机电磁转矩波形图
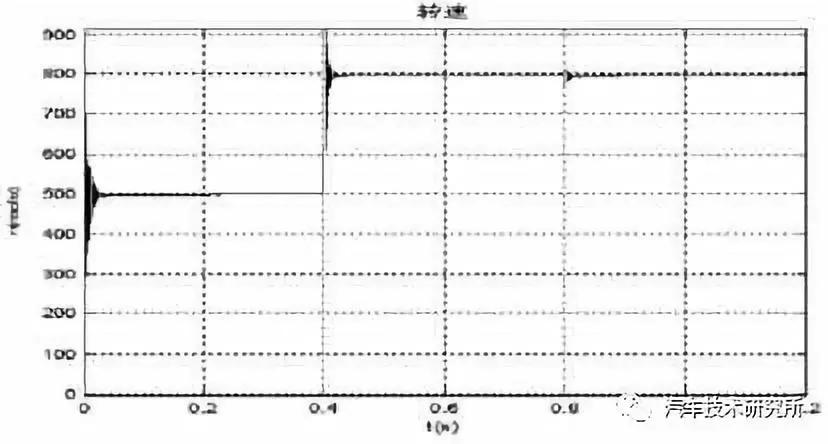
图6 转子侧转速
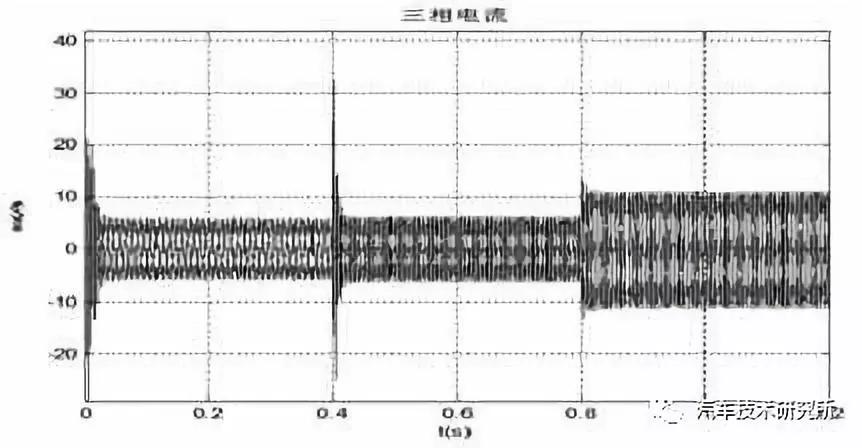
图7 定子三相电流
由图5 可得：在0.4s 时，转速突变，转矩波动时间短且恢复较快，即代表超车加速工况下，电动汽车转矩脉动响应迅速，行驶稳定性能好；在0.8s 时，负载突变，转矩曲线轻度浮动，即代表大力矩爬坡工况下，电动汽车转矩脉动小，行驶稳定性能好。
由图6 可得：在0.4s 时，转速突变，转速响应速度快，说明电动汽车加速性能好；在0.8s 时，负载突变，转速急剧下降，但又可以很快恢复到初始值附近，运行在稳定状态时无静差，说明电动汽车动力性好。
由图7 可得：在两种工况下，电机相电流脉动均不大且波形合理，相电流冲击很小说明系统具有较好的鲁棒性。
通过分析各个仿真图可证明了本文所提出的PMSM 控制系统仿真建模方法的有效性，PMSM 矢量控制系统具有很好的动态响应特性和速度控制特性，控制效果突出，适用于电动汽车多工况运行的情况。
5 结论
本文在结合PMSM 基本原理，对PMSM 进行数学建模，利用矢量控制思想和SVPWM 技术，搭建了基于Simulink 环境下的仿真模型。通过在仿真平台中模拟电动汽车超车加速工况和大力矩爬坡工况进行仿真，根据仿真波形分析得出两种工况下永磁同步电机的特性。由分析结果可知：矢量控制系统稳定性能好，且静、动态特性优秀，与实际的永磁同步电机的运行特性相吻合，且适用于电动汽车多工况运行的情况。采用该仿真系统，可证明数学建模的合理性，且此仿真模型的适用性好，改变各个模块的参数可以适应不同的控制需求。
广告
广告
编辑推荐
最新资讯
-
厂商要多努力，才能让用户听起来毫不费力？
2024-11-22 17:10
-
TOP30！海克斯康入选2024福布斯中国数字科
2024-11-22 15:25
-
揭秘国产装备制造厂商的成功秘籍：好耐电子
2024-11-22 15:24
-
一文详解安全分析方法STPA：以自动紧急制动
2024-11-22 15:20
-
选对涉氢压力表：守护涉氢场所安全的关键一
2024-11-22 15:19
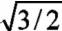
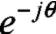
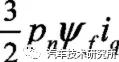
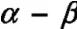
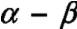
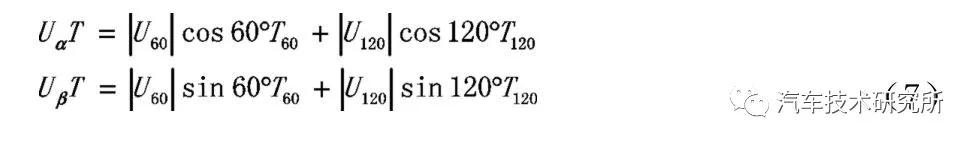
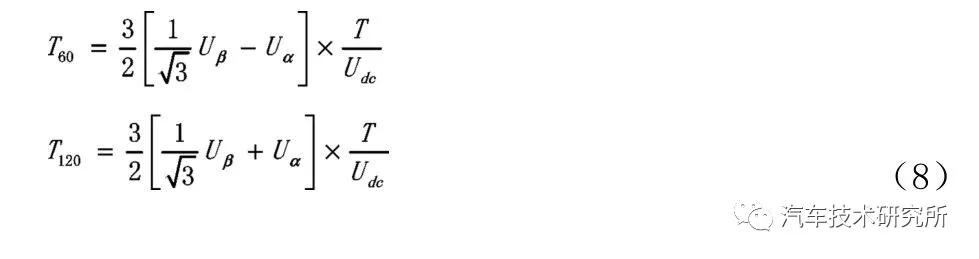
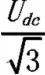
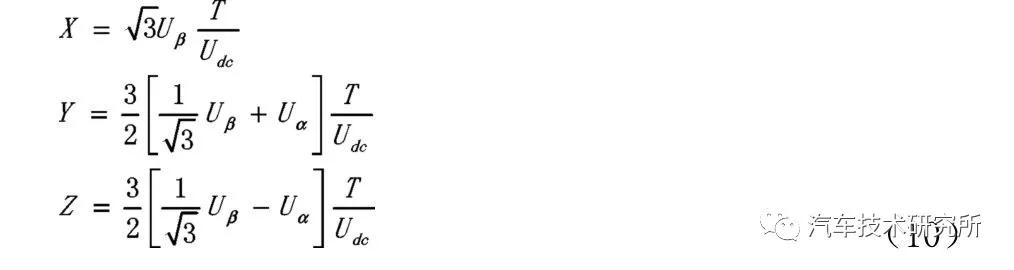
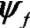
广告
广告
