广告
低速工况下轨迹追踪的转向动力学建模
2019-09-24 23:12:13· 来源：同济智能汽车研究所
编者按：仿真是实车试验前的关键一环，而仿真时使用的车辆模型则直接影响了仿真的精度。现有的仿真系统多使用车辆的二自由度模型，考虑车辆的侧向运动及绕z轴的
编者按：仿真是实车试验前的关键一环，而仿真时使用的车辆模型则直接影响了仿真的精度。现有的仿真系统多使用车辆的二自由度模型，考虑车辆的侧向运动及绕z轴的横摆运动，并假定车速恒定，侧偏刚度为定值，线性二自由度模型忽略了转向系、悬架系统等的影响, 简化分析过程的同时保留了对车辆转向特性、横摆响应的描述, 因此在操纵稳定性研究中得到了广泛的应用。但实际应用中，当到达一定速度时，其精度便会降低，依托其建立的控制器的控制效果也会随之变差，甚至发散。在我们实际使用、改进模型时，如何在尽量少的增加模型复杂度的情况下更准确的模拟实际情况，是重点与难点。
本文译自："Modelling the dynamic behavior of the steering system for low speed autonomous path tracking"
文章来源：2019 IEEE Intelligent Vehicles Symposium (IV)
作者：Ádám Domina, Viktor Tihanyi
原文链接：https://ieeexplore.ieee.org/document/8814185
摘要：在未来，随着高度自动化车辆的出现，驾驶员辅助系统的使用将变得更加普遍。最初，驾驶辅助系统仅仅辅助驾驶员进行驾驶，但必定会逐渐接管整个车辆的控制。在这一过程中，车辆必须自己规划行驶轨迹并安全的地跟踪该轨迹，同时保证乘客的舒适。为了开发出合适的轨迹追踪控制器，必须首先在模拟环境中进行仿真，然后进行实车的测试。 在之前的一篇论文中，作者使用了不同的路径跟踪控制器，并先后进行了仿真与实车测试。在仿真环境中，使用了描述车辆横向动力学特性的单轨模型。仿真和实车测试的结果显示出了一定的差异。本文旨在找出在转向系统的动态特性中出现差异的原因，包括轮胎的影响。在此基础上，我们调整了车型，并进行了测量以识别转向系统和轮胎的动力学。在分析测量结果后，建立了描述转向系统的动力学模型，在此基础上扩展了车辆模型。最后，使用改进后的车辆模型进行了仿真，并与实车试验结果进行了对比，结果表明模型改进后更加贴近实车试验的结果。
1、前言
近年来，自动化系统的车辆收到了汽车制造商们越来越多的关注。驾驶员在驾驶期间执行的任务及其复杂，根据SAE级别，实际可用的，LV3级别以下的自动驾驶系统旨在为驾驶员提供支持以减少他们的负荷。这些系统改善了道路安全性，提高了驾车出行的效率，以及舒适性，同时让我们的出行更加环保。全球正面临着愈加严峻的交通挑战，而自动驾驶是解决这些问题的一剂良药。
为了实现自动驾驶，一方面必须提高车辆的自动化水平，另一方面必须开发智能基础设施和智能运输环境。智能城市和V2X通信的出现就是很好的例子，在后一种情况下，车辆可以与其他车辆或交通基础设施进行通信。未来的自动驾驶车辆必须执行复杂的控制操作，以实现车辆在路上的平稳行驶。这样一个复杂的系统的开发需要将很多的影响纳入考虑。因为为所有可能的场景做准备是一项非常困难的任务，所以开发和测试这样的系统对开发人员来说是一项重大的挑战[1]，[2]。
自动驾驶车辆的控制分为四层。它们分别是驾驶员交互层，环境感知层，决策层和执行层。驾驶员交互层负责进行人机交互。环境感知层监控车辆车辆所处的环境，识别物体，障碍物，交通参与者以及水平和垂直交通标志[3]。决策层根据从其他层收集的数据进行决策和路径的规划。执行层负责车辆的纵向和横向控制，并执行从命令层接收的指令。作为本文主题的路径跟踪算法属于执行层。
本文的主题是路径跟随控制器的开发。首先，在模拟环境中使用车辆模型和相应的控制器来测试算法。在该阶段，实际建模是必要的，否则控制器算法在真实环境中的表现将完全不同，这是控制器的开发过程[5]。软件仿真的优点是可以在软件环境中轻松调整控制器，如果它们正常工作，则可以在真实车辆上进行测试，节省时间和资源。车辆模型越复杂，仿真结果就越接近测量结果。在之前的论文[4]中，作者已经实现了三个路径跟随控制器[6]，[7]，[8]，并且在仿真环境中的单轨动力学模型上对它们进行了测试。在控制器正常运行后，又将其在真实车辆上进行了测试。因为忽略了对车辆行为具有显著影响的真实车辆的许多动力学因素，测试结果与实车试验结果呈现出了一定的差异。随着速度的增加，仿真和实际车辆运动特性之间的差异越来越大。在更高的速度下，真实车辆开始在路径周围振荡，而在模拟中，速度值则没有产生影响。本文是作者前期论文的延续，侧重于评估实车和横向动力学单轨模型之间的差异。在本文中，已经存在且常用的模型[8]，[9]，[10]，[11]，[12]已经通过转向系统和轮胎的动力学进行了升级。
2、试验车辆和改进的车辆模型
图一展示了试验车辆。为了实现最高水平的自动化，布达佩斯技术与经济学院的汽车技术系不断对车辆进行改进。该试验车用于在实践中对研究结果进行测试。该车配备dSpace Autobox，负责车辆控制，摄像头，激光雷达和雷达传感器，以及两个高精度GNSS系统。两个GNSS需要有冗余，如果一个不能以足够的精度工作，另一个仍然可以定义车辆的位置。这对于基于GNSS定位的路径跟踪至关重要。
图1.试验车辆
单轨动力学模型用于模拟结果[4]，其模拟的适用性速度上限为15km / h。
在更高的速度下，仿真与现实之间存在显着差异。模拟中的路径跟踪保持准确，事实上车辆明显偏离轨道。试验中存在有两种典型的缺陷运动。一个是车辆沿路径的摆动运动。另一个是到达弯道时车辆的超调，超调发生在当车辆刚刚到达转弯位置，开始转弯操作时。现实与仿真之间差异的原因是忽略了许多动力学因素。转向系统的惯性和阻力应被纳入考虑——这通常在讨论单个时间常数[13]，或横摆阻尼[14]，[15]以及轮胎的动态特性时被纳入考虑，否则车辆将会在与参考值相比没有任何延迟的情况下达到转向角。如果轨迹跟踪控制器发出的指令发生了延迟，则车辆的转向将在需要转向的点之后发生，这解释了超调和振荡。使用的车辆模型由两个等式描述：
其中Vy是车辆的横向速度，Cf和Cr是前轮胎和后轮胎的侧偏刚度，lf和lr是车辆重心（C.G.）与前后轴之间的距离。δ是转向角，ω是车辆的横摆角速度，Vx是车辆的纵向速度，m是车身质量，Iz是车辆沿z轴的转动惯量。由于纵向速度不变，故忽略了车辆的纵向动力学特性。在测量期间，车辆在轨道到达预定轨迹之前开始加速到期望的速度。在任何情况下，在到达轨道的最后一个点之后停止测量。这意味着在模拟中将Vx的值调整为常数不会导致模拟和测量之间的任何差异。方程式由描述转向动力学的第三个方程补充：
其中Mmot是电动转向伺服电机产生的扭矩。 Mtire是转向阻力矩，由车轮绕其垂直轴（z轴）旋转时，橡胶与沥青路面的摩擦产生。Msa是回正力矩，icw是转向系统的传动比。Θ是转向系统的转动惯量，包括转向柱，小齿轮，齿条，轮毂和车轮。是转向柱的角加速度。所描述的扭矩是包含多个因素的函数，在下文中，将定义这些扭矩。
A．转向系统的惯性
创建转向系统的模型需要知道转向系统转动惯量（Θ）[17]。如果（3）式中的Mtire和Msa的值为零，则可以确定Θ。当车辆以零速度移动并且轮胎与地面之间没有摩擦时，会发生这种情况。由于速度为零，Mtire为零，由于没有摩擦，Msa为零。当汽车被升起时会发生这种情况。因此，抬起车辆进行测量，以计算Θ的值。在这种状态下，（3）式可以简化为（4）式。
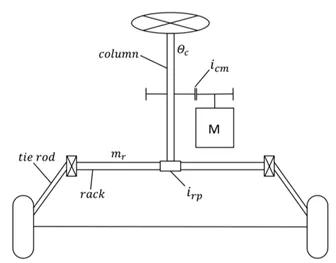
图2.转向系统运动模型
在测量期间，考虑到Mmot不是电动机轴上的扭矩，而是转向柱上的扭矩，将记录转向角（δ）和电动转向伺服发动机扭矩（Mmot）在转向柱上的值。在测量期间，在指定的扭矩值下测量转向柱的旋转。可以通过求取δ的二阶导数来计算转向柱的角加速度，而Θ的值可以由（4）计算。计算得出的θ值是整个转向系统换算到转向柱的总惯性。 “图2“显示了转向系统的运动学布置。测量结果显示Θ的值为0.00345kg * m2。
B． 回正力矩
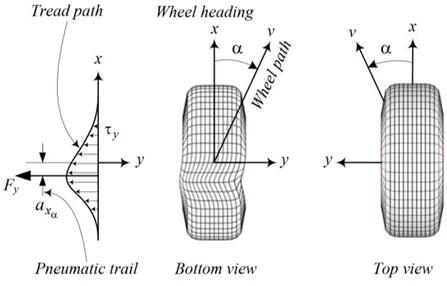
当车辆在弯曲的轨迹上移动时，侧向力（Fy）会对车辆产生影响。侧向力将经由轮胎与地面之间的摩擦关系传递。横向力位于轮胎印迹中心线后面的axα处。这个距离称为轮胎的拖距。由此产生了回正力矩Msa，其使车轮绕其z轴旋转，并且倾向于减小侧偏角α。 “图3”显示回正力矩的原理。
图3.回正力矩
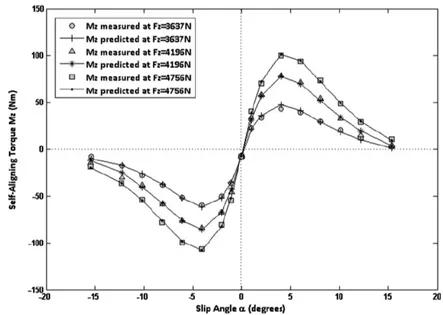
图4.轮胎的侧偏角-回正力矩特性
回正力矩的值是由轮胎和车辆确定的，其确定需要复杂的测量系统。因此，我们基于侧偏角的知识，从实验数据确定回正力矩。 “图4“显示了在不同载荷下的测量数据，回正力矩表示为侧滑角的函数。使用车辆模型计算侧滑角，因此可以使用图4中的图表确定Msa.试验车的前轴载荷为380 kg，这与最小轴载的测量数据相差很小，因此可以使用。在图4中，使用圆圈标记了相应的数据集。该图将Msa定义为侧偏角角Msa（α）的函数。
C． 转向阻力矩
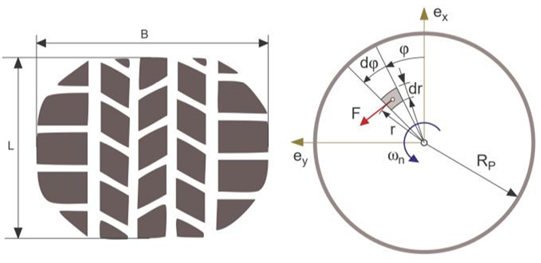
式（3）中的扭矩是由轮胎与路面之间的摩擦引起的。“图5“表示出了接触面和计算转向阻力矩的原理。
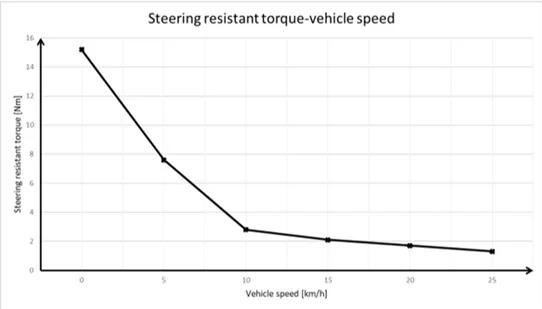
转向阻力矩是车速的函数。扭矩大小与速度成反比，车辆速度越快，其值越低。当车速为零时转向阻力矩最大。
在“图 5“中，F是切向力，它是由在半径r上的每个dA单元产生的。知道摩擦系数μ后，可以通过F =μ* Fz计算F。根据（5）[20]，要计算Mtire，必须将整个接地区域积分。
其中A为整个接触面积。
图5.转向阻力矩的近似处理
图6.转向阻力矩-车速对应关系图
由于压力分布和摩擦条件未知，因此以不同的速度进行测量以确定转矩。在测量期间，在转向柱上施加扭矩，并在不同的车速下测量转向柱的旋转。只有在（3）中已知Msa和Θ才能确定Mtire，因为在这种情况下，Mtire是等式中唯一未知的：Msa由图4确定，Θ已知，δ由测量得到。测量从0 km / h开始，在所有测量中每次将速度提高5 km / h，最高达25 km / h。 “图.6“展示了测量结果。测量结果表示为当前速度下的转向扭矩值。在所有相邻点之间通过线性插值来计算每个点之间的扭矩值。在有了这些作为基础之后，我们在软件环境中创建了转向系统的动态模型。
3、仿真结果与试验结果的比较
在完成车辆模型的开发之后，运行模拟。预期结果将尽可能接近实际车辆测量值，但仿真不会与测量结果完全匹配。如果仿真结果本质上接近测量结果，那么车辆模型可以认为是可接受的，因为总是会存在环境的随机影响和模型的不准确性，而导致不能实现完美匹配。最重要的是仿真中应存在缺陷形式的运动，它们的具体值并不重要，因为随机效应对其有着显着的影响。在振荡中，路径的偏移量和振荡频率是比较的基础标准。测量和模拟的振荡不需要同相。
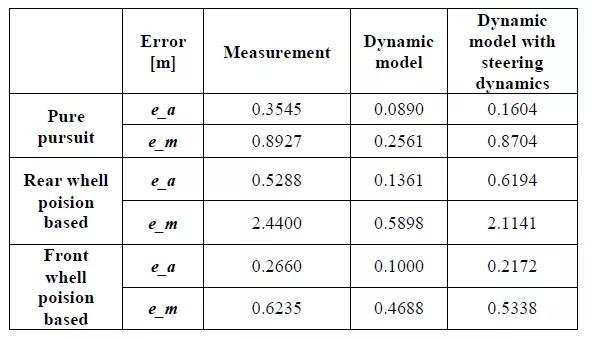
在超调的情况下，超调的位置和程度是最重要的。即使在振荡和超调的情况下，它们的存在也足以得出关于模拟结果的真实性的结论，并且如果必要的话，可以进一步开发路径追踪控制器。在本章中，比较了模拟和测量结果。在每个图中，黑线表示参考路径，绿色表示车辆的记录路径，红色表示侧向单轨动力学模型的仿真结果，蓝色表示改进的单轨动力学模型的仿真结果，其中包含了转向动力学。“表1”表示横向误差，用误差的均方根表示，E_a表示平均侧向误差，E_m表示最大误差。
A. 仿真结果——基于后轮位置的控制器
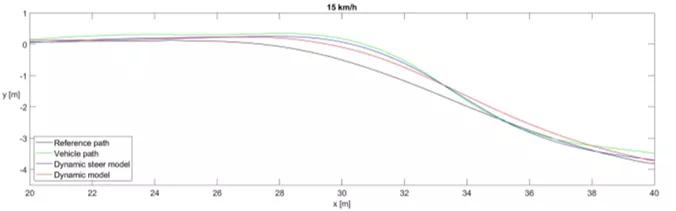
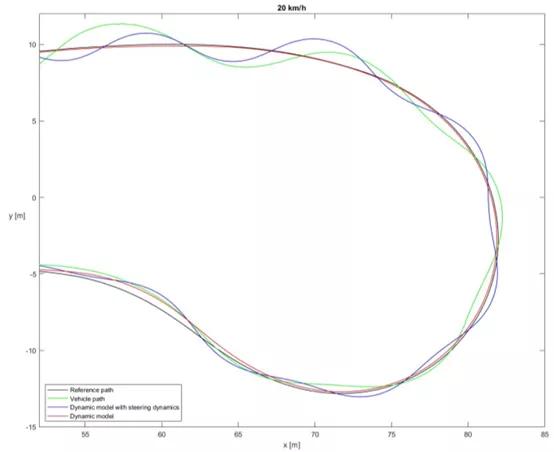
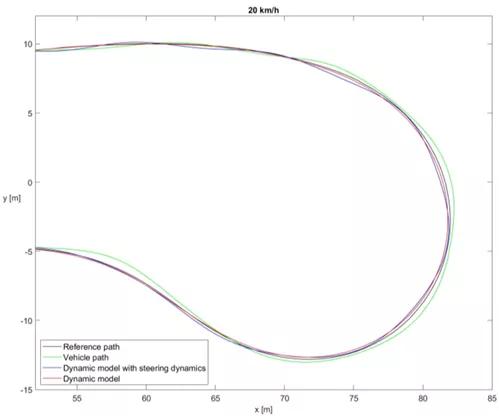
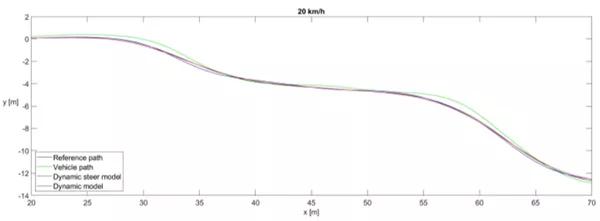
基于后轮位置的控制器的仿真结果如图7，图8所示。在控制器调整期间的模拟中，车辆准确地跟踪轨道，如图7中的红线所示。在该模拟中，使用横侧向单轨动力学模型。在测量期间，该控制器显示出了不稳定性，倾向于振荡，特别是在较高速度范围内，在20km / h时，由于不稳定，车辆变得危险，因此必须中断测量。如图8中的绿线所示，在转弯操纵中存在显着的超调。在包含转向动力学的改进模型的模拟中，模拟结果显示与测量相同的运动形式。振荡完全相同，其频率，幅度和相位与测量结果一致。模拟非常接近测量结果。通过提高速度，车辆以与测量期间相同的方式变得不稳定。进一步的结果如图7所示，这说明了超调的结果。改进的车辆模型模拟超调更准确，结果明显更接近测量结果。超调也出现在更简单的模型中，但它比测量值小。
图7.基于后轮位置的控制器——在15km/h时的小s型曲线结果
（图中黑线为参考路径，绿线为实车试验时的车辆路径，红线为改进前的单轨模型的仿真结果，蓝线为改进后的动力学模型的仿真结果）
图8.基于后轮位置的控制器——在20km/h时的反转曲线结果
仿真结果证实了测量结果，后轮位置控制器适用性的上限为15 km / h。控制器调整到了更简单的模型，因此在改进的模型上重新调整它可以改善其性能，最大化其可用性。这也适用于此处讨论的其他控制器。
B．纯路径追踪控制器
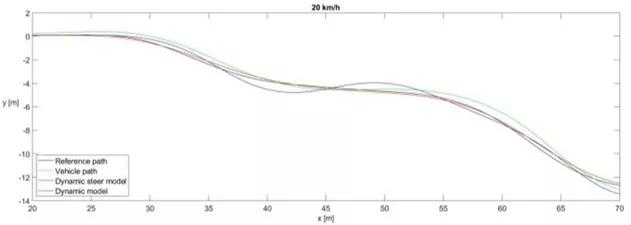
纯追踪控制器的仿真结果如图9和图10所示。采用纯追踪控制器，改进后的模型也能更准确地返回结果。震荡也在仿真中精确地再现，但是在仿真中幅度不太准确。存在过调，其程度被夸大了。
改进车型的仿真结果靠近纯追踪控制器的测量结果，其上限为20 km / h。
图9.纯追踪控制器——在20km/h时的小s曲线结果
图10.纯追踪控制器——在20km/h时的反转曲线结果
C．基于前轮位置的控制器
纯追踪控制器的仿真结果如图11和图12所示。仿真中出现了振荡，其频率接近测量结果。使用改进模型的仿真中的超调比旧模型更接近测量结果。根据仿真结果，基于前轮位置控制器的适用范围与测量结果相同，其上限为20 km / h。
图11基于前轮位置的控制器——在20km/h时的反转曲线结果
图12基于前轮位置的控制器——在20km/h时的小s曲线曲线结果
表1.侧向误差——20KM/h
4、结论
本文中，改进了作者在前一篇文章中使用的车辆模型。之前的模型仅包含车辆横向动力学的一部分。使用该模型，测量和模拟结果之间存在着显着的差异。基于该模型的仿真结果仅可达15 km / h。
因此，考虑到转向系统和轮胎的动态特性，该模型得到了进一步发展。改进的车辆模型的结果接近于测量结果，将模拟的适用性扩展到了至少20km / h。阐述了转向系统的模型，用测量来辨识系统，并且确定其转动惯量。建立了车速和轮胎转动阻力矩之间的关系。通过改进的模型，进行了仿真。
最后，对仿真结果进行了比较，仿真结果与测量结果具有良好的相关性。
联系人：李老师
电话：021-69589225
邮箱：11666104@tongji.edu.cn 
广告
广告
最新资讯
-
汽车网络安全法规(R155&R156)和标准(ISO 21
2024-11-18 07:56
-
氢内燃机实车示范运行在天津正式启动
2024-11-18 07:53
-
氢燃料电池卡车创企“冰河时代”！HVS命悬
2024-11-17 09:45
-
小米端到端大模型：智能驾驶的“新大脑”
2024-11-17 09:44
-
阿斯顿马丁推出新款 F1 模拟器
2024-11-17 09:43
广告
广告
