广告
同步器换挡过程动力学建模分析与实验
2020-02-09 12:26:10· 来源：EDC电驱未来 作者：张志刚
1 换挡机理1.1换挡过程简介惯性同步器主要分为锁环式与锁销式两种,本文主要研究锁环式同步器,其主要由待接合齿圈、接合套、滑块、压簧、同步环、摩擦锥环、花键
1 换挡机理
1.1换挡过程简介
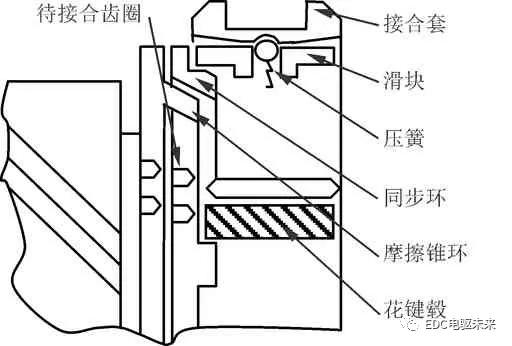
惯性同步器主要分为锁环式与锁销式两种,本文主要研究锁环式同步器,其主要由待接合齿圈、接合套、滑块、压簧、同步环、摩擦锥环、花键毂等组成,具体结构如图1所示。
图1 同步器结构简图
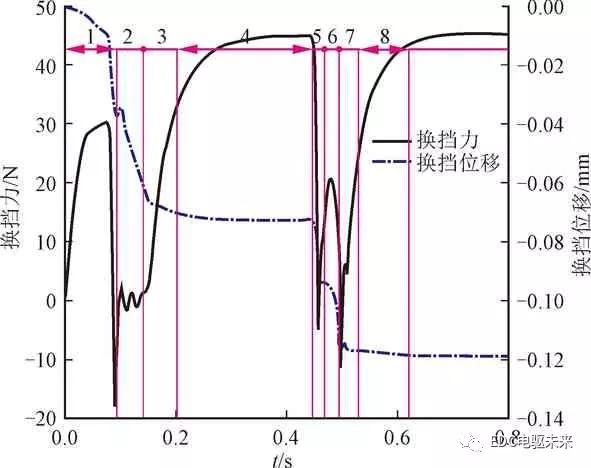
同步器换挡过程主要可以划分为摘挡、滑移、预同步、同步、拨环、二次冲击、齿轮拨转、齿轮啮合等8个阶段,如图2所示。
1:摘挡;2:滑移;3:预同步;4:同步;5:拨环;6:二次冲击;7:齿轮拨转;8:齿轮啮合
图2 同步器换挡过程划分
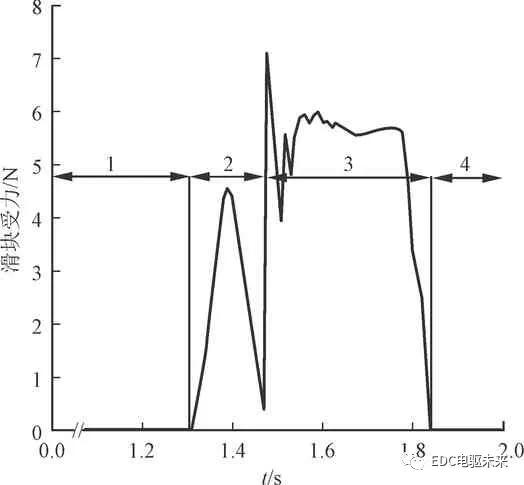
同步器的主要功用是在较短时间内使得变速器输入输出端转速同步,预同步与同步阶段同步器对同步性能有着重要影响。在预同步阶段,接合套带动滑块做轴向运动。整个阶段滑块受力分析如图3所示。
1:摘挡;2:滑移;3:预同步;4:同步
图3 滑块受力分析
滑移阶段滑块受到轴向力开始做轴向运动,预同步阶段滑块推动同步环继续向摩擦锥环做轴向运动。由于同步环与摩擦锥环间存在润滑油,当同步环向摩擦锥环轴向运动时两环之间会产生黏性转矩。在黏性转矩作用下,同步环被错开半个齿,接合套被锁止。当换挡力进一步增加时,滑块锁止定位机构失去平衡,被压入接合套内的凹槽之中,此时滑块轴向力消失,预同步阶段结束。
同步阶段由于换挡拨叉轴向力作用,同步环继续向摩擦锥环做轴向运动,存在同步环与摩擦锥环间的润滑油被挤压到间隙外。在此过程中,由于两摩擦表面微凸体接触与油膜剪切产生了粗糙摩擦转矩和黏性剪切转矩。在两种转矩的共同作用下,同步器输入输出端实现了同步。
针对同步器同步机理,分别建立油膜压力、微凸体接触压力、同步环承载力、同步力矩4个模型。
1.2 油膜压力
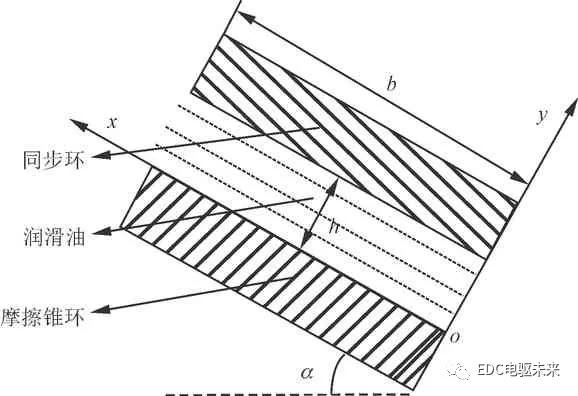
同步过程中同步环与摩擦锥环相对转动,作用在接合套上的轴向力使得同步环与摩擦锥环之间的间隙不断减小,间隙内的润滑油被挤出或渗透到摩擦锥环表面。根据同步环和摩擦锥环结构特点与润滑油物理特性可知,间隙内润滑油运动规律满足雷诺方程。针对同步环和摩擦锥环之间油液的挤压运动,以同步环摩擦表面切向方向为x轴,以垂直于同步环摩擦表面方向为y轴,建立同步器同步过程中油液挤压模型二维坐标系,如图4所示。
b:同步环宽度;α:摩擦锥角;h:同步环与摩擦锥环摩擦表面平均间隙
图4 同步环与摩擦锥环结构示意图
通过对同步环与摩擦锥环间的油液变化规律分析可以发现:①同步环与摩擦锥环之间的油液成轴向对称分布;②圆周方向油膜厚度为一常数;③两摩擦表面接近速度为dh/dt。
在考虑压力流量因素和材料渗透性下,假设同步环摩擦材料厚度为d,同步环与摩擦锥环间润滑油的运动规律满足
(1)
式中:p为同步环所受油膜压力;h为同步环与摩擦锥环摩擦表面平均间隙;Φ为摩擦副渗透性;φx为x轴方向Patir和Cheng压力流量因数。
假设同步环和摩擦锥环两表面粗糙峰高度都服从均值为0的高斯概率分布,则有
(2)
式中:hoil为两摩擦表面间油膜厚度;erf(·)为误差函数。
油膜压力边界条件代入式(1),求得油膜压力为
(3)
式中
1.3 微凸体接触压力
假设同步过程中同步环与摩擦锥环之间只发生弹性摩擦,则摩擦副微凸体接触压力为
(4)
式中:H=hoil/σ为膜厚比;λ为摩擦表面粗糙峰密度;R为粗糙峰曲率半径;σ为两摩擦表面联合粗糙度,分别为同步环和摩擦锥环表面粗糙度;E′为摩擦副当量弹性模量;A为名义接触面积;Fn(H)为膜厚比相关函数。E′、Fn(H)分别为
(5)
Fn(u)=(s-u)nφ*(s)ds
(6)
式中:E1、E2分别为摩擦锥环和同步环的弹性模量;υ1、υ2分别为摩擦锥环和同步环的泊松比;φ*(s)为摩擦表面峰顶高度的高斯概率密度函数。
同步环摩擦材料为铜基粉末冶金,摩擦锥环材料为高碳钢,λβσ=0.05,σ/β=0.011 3,E′=2.7×108Pa。
1.4 同步环承载力
同步过程中同步环承载力由油膜压力和微凸体接触共同承载,即
Ftotal=(1-B)Foil+BFc
(7)
式中:Foil为油膜压力;Fc为微凸体压力;B为微凸体接触面积与名义接触面积之比
(8)
其中0≤B≤1。当B=0时表示同步环承载力全部由油膜压力承担;当B=1时表示同步环承载力全部由微凸体压力承担。根据所建坐标系,求得Foil、Fc分别为
(9)
(10)
通过对同步环受力分析可知,同步环承载力Ftotal等于接合套所受轴向力Fsleevesinα。结合式(4)和式(9)～(12)可解得油膜变化率为
(11)
1.5 同步力矩
同步力矩T主要由黏性转矩Toil和微凸体接触摩擦转矩Tc共同组成,即
T=(1-B)Toil+BTc
(12)
(13)
(14)
式中:fc为滑动摩擦系数,fc=0.13+0.008lgω。
依据变速器升降规律,其同步力矩为
(15)
式中:I为同步器输入端等效转动惯量;ωi为摩擦锥环与同步环之间的转速差。将式(13)～(15)代入式(12)整理可得
(16)
2 同步器动力学模型
2.1 联合仿真模型
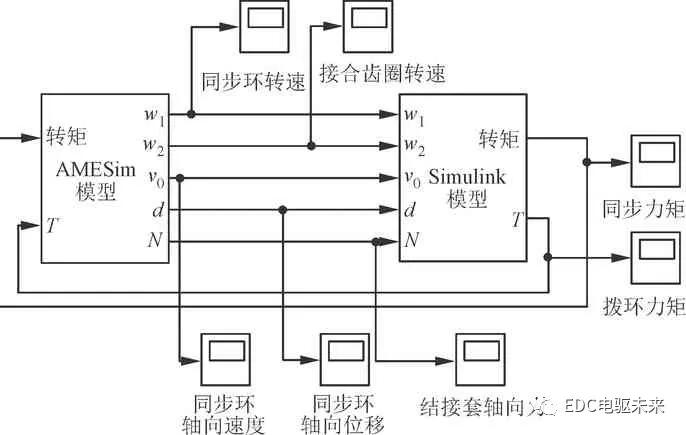
基于所建数学模型,利用Simulink建立同步器摩擦模型,其中AMESim模型为Simulink模型调用模块。Simulink模型包括油膜厚度、转速差、同步力矩(黏性转矩与微凸体接触摩擦转矩)以及拨环力矩(即同步过程中接合套作用于同步环上使得同步环相对于接合套有相对退转趋势的力矩)计算模块,其所建同步器Simulink摩擦模型如图5所示。
图5 同步器Simulink仿真模型
将AMESim中计算的接合齿圈转速、同步环转速、同步环轴向运动速度、同步环轴向位移、同步环所受轴向力输入到Simulink模型中;根据所建的油液剪切模型和微凸体接触模型,运用4阶Runge-Kutta方法对转速差和油膜厚度求解。
将所得同步力矩输入到AMESim模型中,实现AMESim与Simulink同步仿真。同时,将Simulink模块中所计算的拨环力矩输入到AMESim模型,从而准确控制同步器换挡过程中的拨环过程。同步器动力学联合仿真模型如图6所示。同步器物理模型由AMESim中机械结构模块搭建,摩擦模型由Simulink调用求解。仿真过程中同时打开两个模型,AMESim模型模拟同步器机械运动过程,Simulink模型解析同步器摩擦过程。
图6 同步器动力学联合仿真模型
2.2 数值求解
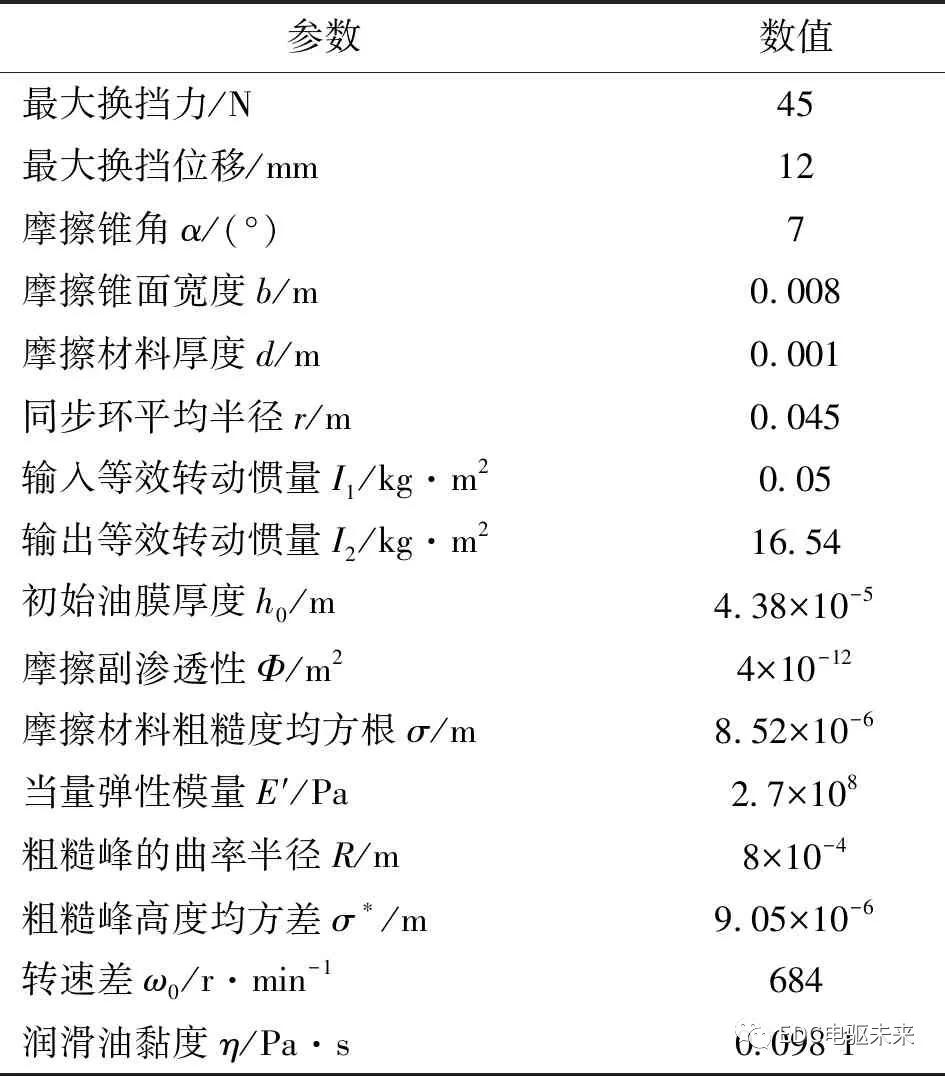
基于某款国产变速器实测数据,建立同步器动力学联合仿真模型,相关参数见表1。
表1 同步器动力学联合仿真模型相关参数
将初始数值输入到所建动力学联合仿真模型,采用4阶Runge Kutta方法对式(11)和式(16)进行耦合求解,同步计算出油膜厚度和转速差。将AMESim模型中计算所得初始油膜厚度和转速差输入到Simulink模型中,并将每次求解得到的油膜厚度和转速差作为下次迭代的初始值。微分方程迭代步长为0.001,当转速差小于0.001 r·min-1时,默认为同步完成。
2.3 仿真结果
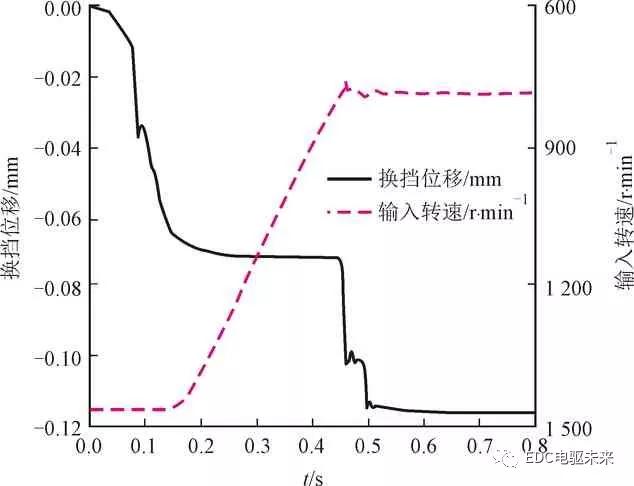
运用所建同步器动力学联合仿真模型对换挡过程进行仿真,其换挡力、同步力矩、换挡位移以及输入转速的仿真结果如图7所示。由图7可知,所建模型能够对换挡过程中的换挡力、同步力矩、换挡位移、输入转速的变化规律进行仿真。由图7a可知,所建模型换挡力仿真结果能够对换挡过程中的摘挡、同步、二次冲击、齿轮啮合等阶段进行模拟,同步力矩仿真结果能够体现同步器同步过程。由图7b可知,换挡位移与输入转速变化趋势具有相关性。在同步过程中输入转速不断减小,换挡位移保持不变。所建模型能够对换挡位移与输入转速的变化规律进行仿真。
(a)换挡力与同步力矩
(b)换挡位移与输入转速
图7 同步过程的仿真结果
3 同步器动力学联合仿真模型实验验证
3.1 同步器换挡性能测试系统
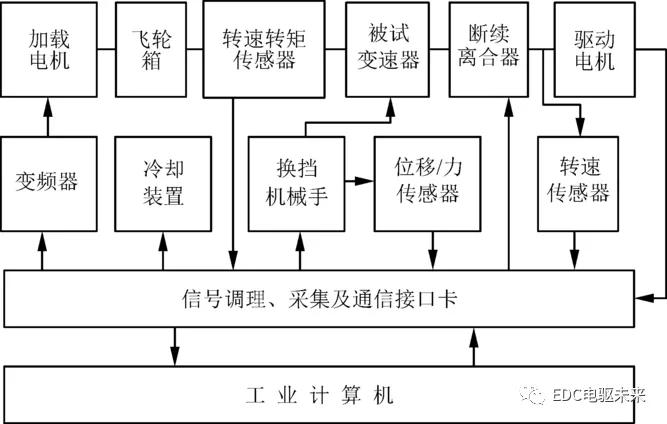
为了满足同步器换挡性能实验测试需求,设计开发了同步器换挡性能测试系统,如图8所示。
(a)结构原理图
1:换挡机械手;2:被试变速器;3:转速转矩传感器;4:惯量盘;5:加载电机;6:冷却装置
(b)实验台实体
图8 同步器换挡性能测试系统
3.2 实验结果
基于自主开发的同步器换挡性能实验台,对所建模型进行了实验验证。为确保仿真与实验结果的一致性,参照仿真条件以及同步器实际工作环境设置实验工况,具体同步器换挡测试实验相关参数见表2。
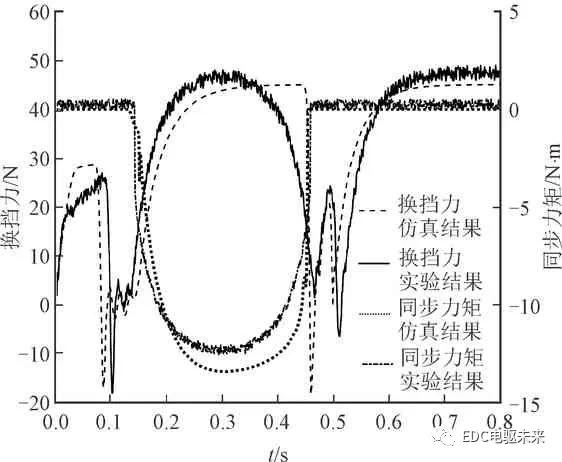
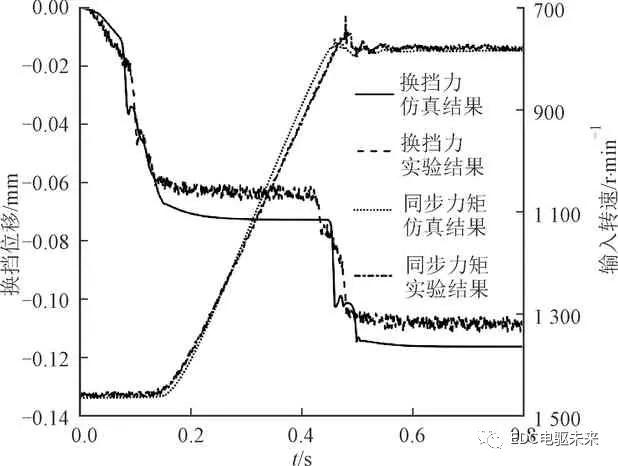
提取实验与仿真中的换挡力、换挡位移、同步力矩、输入转速等数据进行对比分析,验证所建模型的准确性。按照实验大纲要求,在相邻两挡间交替换挡,并采集相应数据。测得的1→2挡的换挡力、同步力矩、换挡位移、输入端转速与仿真分析结果的对比分别如图9、图10所示。
由图9可知,所建模型能够对换挡力和同步力矩进行有效预测。换挡力实验结果与仿真结果变化趋势基本一致,换挡力最大误差值为5.03 N,同步力矩最大误差值为2.94 N·m。仿真结果中摘挡、同步以及二次冲击阶段存在一定误差,产生此现象的原因有:一是因为在实验过程中,换挡实验员虽经过专业培训,但所施加的换挡力大小还是存在一定误差;二是因为所建模型中系统阻尼与实验被测系统阻尼存在一定误差,模型所计算出同步力矩实验结果与仿真结果的变化规律基本一致,但由于所建模型中摩擦系数变化规律欠准确,且被试同步器只进行了磨合实验,所以在同步阶段同步力矩实验结果略小于仿真结果。
表2 同步器换挡测试实验相关参数
图9 换挡力和同步力矩的实验与仿真结果对比
图10 换挡位移和输入转速的实验与仿真结果对比
由10可知,所建模型换挡位移仿真结果与实验结果变化基本一致,其换挡位移最大误差为11 mm,输入端转速最大误差为31 r·min-1。由于仿真模型与实验对象中各个间隙存在一定误差,在摘挡、同步以及二次冲击阶段换挡球头位置略有不同,故换挡位移实验与仿真结果有一定的误差。所建模型能够有效预测同步器输入端转速。由于油液阻力和空气阻力的影响,同步阶段输入转速实验结果下降速率小于仿真结果。在齿轮啮合阶段,由于实验过程中换挡力大于仿真换挡力,所以在同步完成后实验输入转速略大于仿真结果。
3.3 误差分析
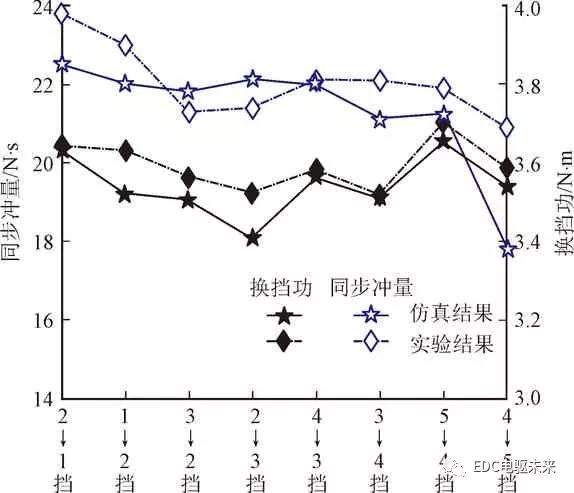
为了进一步验证所建模型准确性,对被试变速器中各挡位同步器进行了实验验证。为了定量评价所建模型的准确性,采用同步冲量与换挡功对仿真结果与实验结果进行定量分析,结果如图11所示。
图11 同步冲量与换挡功实验仿真对比结果
由图11可知,各挡位同步器实验结果的同步冲量比仿真结果略小,这是由于在实际进行同步器换挡性能实验过程中,同步器各旋转部件受到了变速器油液阻尼影响。低挡位的同步冲量大于高挡位,产生此现象的原因是低挡位间的传动大,同步器输入输出端转速差大,同步时间延长。进行动力学仿真时,在参数一定的情况下二次冲击一定会发生,而在进行同步器换挡性能实验时,二次冲击的产生是随机的,故各挡位仿真结果的换挡功略大于实验结果。
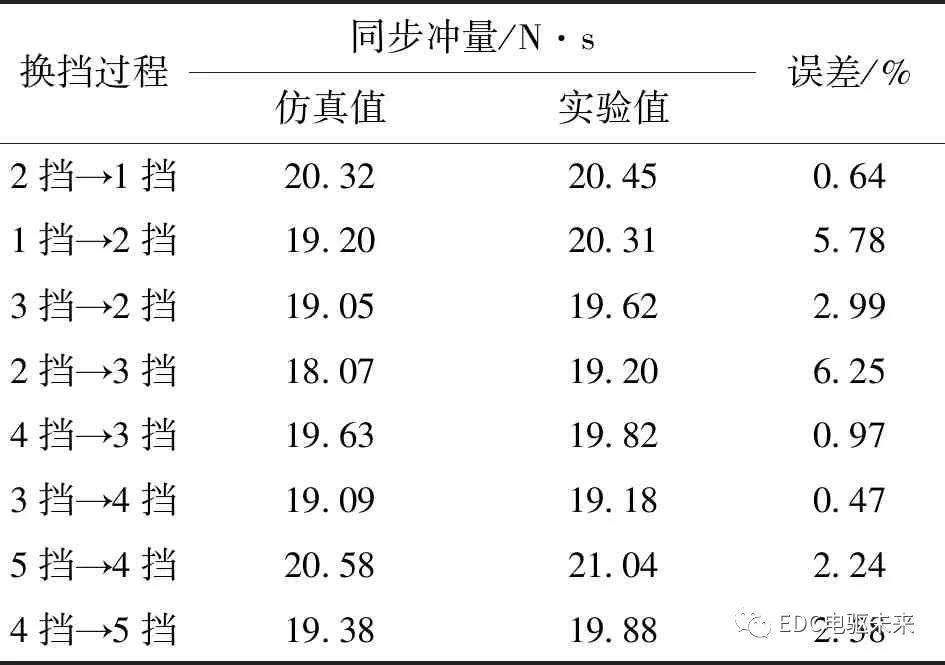
为定量分析所建模型的误差大小,将同步冲量和换挡功的仿真结果与实验结果进行统计分析,结果如表3、4所示。
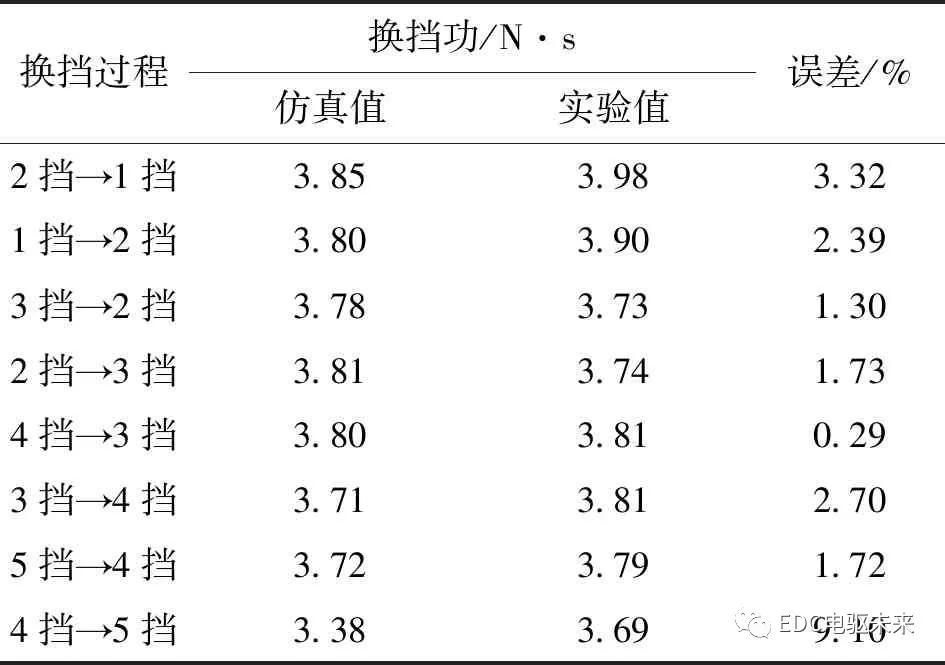
由表2可知,同步冲量仿真与实验结果误差较小,最大误差为6.25%,最小误差为0.47%。由表3可知,各挡位仿真的换挡功与实验结果的一致性较好,最大误差为9.10%,最小误差为0.29%。同步冲量与换挡功的误差值均小于10%,故所建动力学仿真模型能够表征同步器换挡机理。
表3 不同换挡过程的同步冲量对比结果
表4 不同换挡过程的换挡功对比结果
4 结 论
通过对同步器换挡过程的分析,建立了油膜压力、微凸体接触压力、同步环承载力以及同步力矩4个数学模型,基于所建数学模型建立了动力学仿真模型,并对所建模型进行了实验验证,结果表明:
(1)所建模型能够对换挡过程中的换挡力、同步力矩、换挡位移、输入转速等变化规律进行有效仿真;
(2)各挡位工况下的同步冲量仿真与实验结果误差较小,最大误差为6.25%,最小误差为0.47%;换挡功仿真与实验结果的一致性较好,最大误差为9.10%,最小误差为0.29%。
广告 
广告
编辑推荐
最新资讯
-
突然解散！又一智驾公司总部封楼！
2025-02-24 12:09
-
【直播预告】当"双碳"遇上高压快充：破局新
2025-02-24 12:08
-
直播｜车载高速以太网测试技术线上研讨会
2025-02-24 11:11
-
【方案】安全气囊高压钢瓶测试
2025-02-24 10:55
-
直播｜德赛西威：智能驾驶域控制器以太网测
2025-02-24 10:54
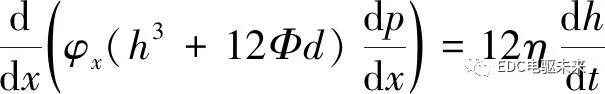
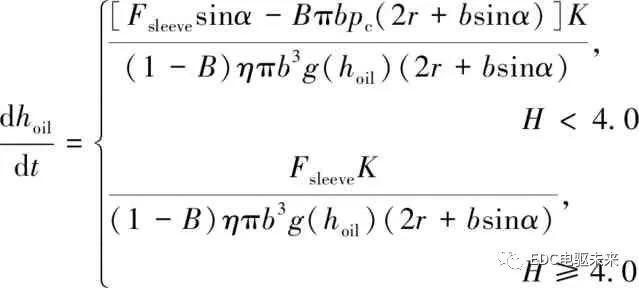
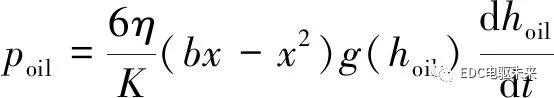
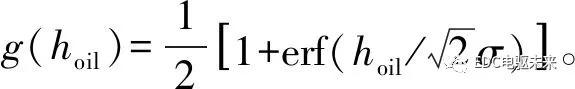
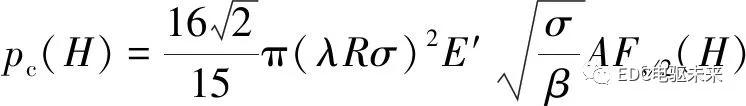
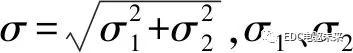
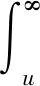
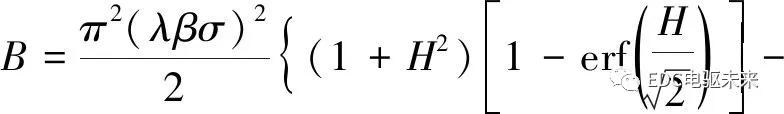
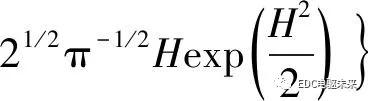
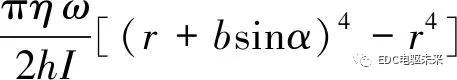
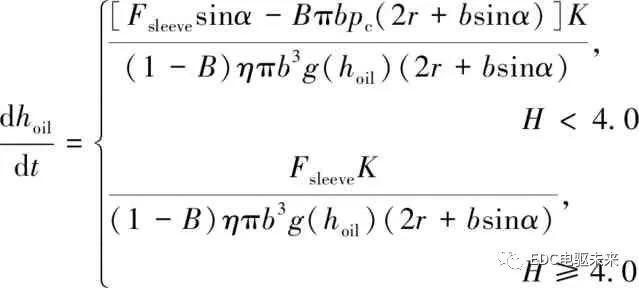
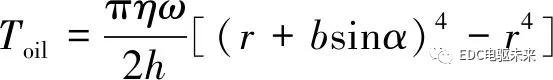
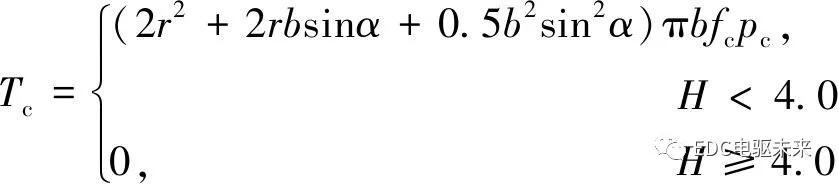
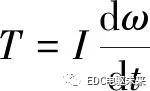
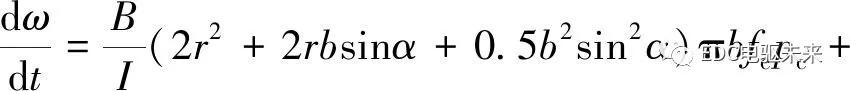
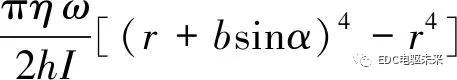
广告
广告
