广告
疲劳损伤谱(FDS)的基本原理
2020-03-10 00:41:47· 来源：模态空间 作者：王朋波
原创 前天01概述我们在进行车辆可靠性耐久性研究时，需要设法对耐久载荷的强度进行量化评估，伪损伤值是最常用的一种手段。伪损伤值不考虑具体结构，直接把各种
01 概述
我们在进行车辆可靠性耐久性研究时，需要设法对耐久载荷的强度进行量化评估，伪损伤值是最常用的一种手段。
伪损伤值不考虑具体结构，直接把各种载荷信号都看作广义应力，以广义应力为输入，使用指定的标准SN曲线，再按照与计算真实疲劳损伤相同的方式进行循环计数和损伤累积。
伪损伤值因为计算简单，且只是信号本身的特性，不涉及具体结构，所以在整车及零部件耐久试验中获得了广泛应用。伪损伤值的最大局限性在于其忽略了信号的频域特性，对载荷强度只能粗略评估，无法体现载荷作用于不同固有频率的结构时的差别。
疲劳损伤谱（Fatigue DamageSpectrum，简称FDS）也是载荷信号本身的一种特性。疲劳损伤谱描述了载荷信号作用于单自由度振动系统所造成的疲劳损伤值与单自由度系统固有频率之间的关联。因为它考虑了频率的影响，与伪损伤值相比，能更准确的反应载荷信号对实际结构的破坏能力。
02 疲劳损伤谱的计算流程
疲劳损伤谱的计算流程简述如下：
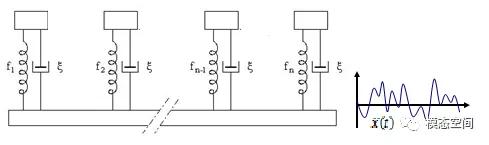
1.将载荷信号施加于图1所示的一系列线性单自由度质量-弹簧系统，分别计算出各单自由度系统相对于支座的位移的时间历程z(t)。
2.单自由度系统的应力与相对位移z(t)成正比，所以我们可得到应力的时间历程σ(t)=Kz(t)。
3.对应力时间历程σ(t)进行峰谷值编辑和雨流计数，提取出应力循环。
4.使用标准SN曲线，根据Miner线性损伤累计准则，计算出每个单自由度系统的疲劳损伤值。
5.最后以单自由度系统的疲劳损伤值D为横轴，以单自由度系统的固有频率f0=ω0/2π为纵轴，绘制成一条曲线D(f0) ，该曲线就是载荷信号的疲劳损伤谱。
单自由度系统的阻尼特性会影响其应力响应值，所以计算疲劳损伤谱之前需要指定阻尼参数，通常指定阻尼比ξ=C/2√Km，也可指定品质因子Q=1/2ξ。
图1 用于计算疲劳损伤谱的单自由度振动系统
计算疲劳损伤谱所用的SN曲线不是某种材料的实际曲线，而是简化的标准曲线，通常使用双对数坐标系下的斜直线，如图2。
图2 计算疲劳损伤谱所用的标准SN曲线
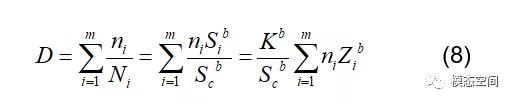
图2展示的循环寿命N和应力幅值S之间的关系，可用下式表示。
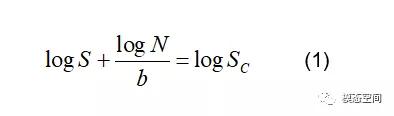
其中b和SC分别为图2中SN曲线的斜率倒数和截距（即SN曲线延长线与Y轴的交点）。斜率倒数b的数值一般要求在-1到-10之间，其中常用数值有-3、-4、-5、-7等。截距SC的数值设定则无严格规定。
总之，计算信号的疲劳损伤谱，需要设定四个常数，即阻尼比ξ、SN曲线的斜率倒数b、SN曲线的截距SC、系统应力与相对位移之比K。
其中ξ和b的取值将影响疲劳损伤谱曲线的形状，设定时必须格外慎重，应尽量符合实际情况。而SC和K的取值改变只会导致疲劳损伤谱曲线沿Y轴缩小或者放大，曲线形状并不会变化。
大多数情况下，我们并不关心某个信号的疲劳损伤谱绝对数值，而只关心不同信号疲劳损伤谱之间的对比。对于多个载荷信号，只要采用相同的SC和K，无论具体取值如何，它们的疲劳损伤谱的比例关系保持不变。所以我们不需过于纠结SC和K如何设定。可将K的数值和SC的取值都设定为1.0以简化计算，也可参照计算伪损伤值时的做法，将SC设置为系统应力σ(t)最大幅值的5倍，即
03 正弦载荷信号的疲劳损伤谱
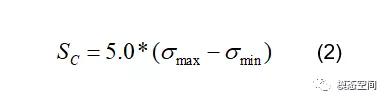
下面我们以正弦载荷信号为例，来介绍疲劳损伤谱的具体计算过程。
图3 承受正弦加速度载荷的单自由度系统
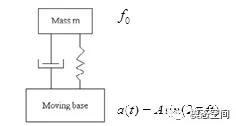
如图3，固有频率为f0（圆频率ω0=2πf0），阻尼比为ξ的线性单自由度系统，支座施加正弦加速度载荷a(t)=Asin(2πft)，载荷持续时间为T。显然，单自由度度系统中质量m的相对位移z(t)也是正弦变化，z(t)的幅值为
根据Miner线性损伤累积准则，正弦载荷作用T时间后，系统的损伤值为
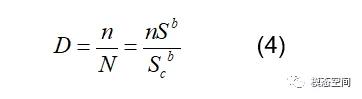
其中n=fT为载荷循环次数，S为应力幅值。
应力幅值与相对位移幅值存在比例关系S=KZm ，所以
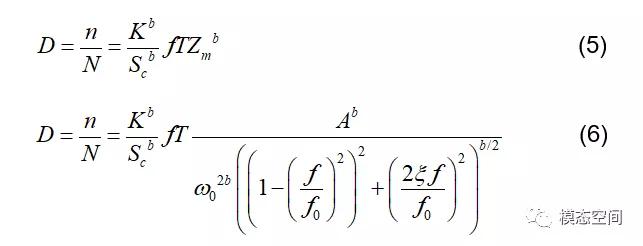
根据式(6)，我们可绘制出正弦载荷的疲劳损伤谱，如图4。单自由度系统的疲劳损伤在共振点达到最大值，此处f0的取值为
图4 正弦加速度激励信号的疲劳损伤谱曲线
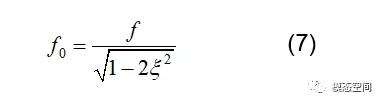
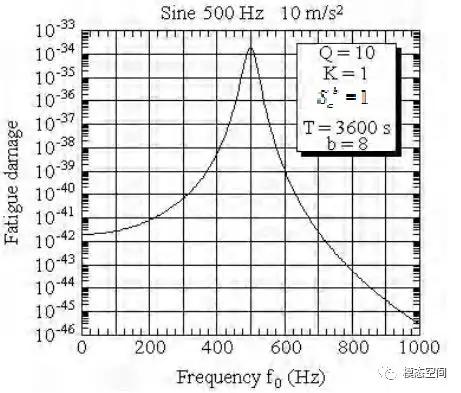
04 随机信号的疲劳损伤谱
随机载荷信号可以用时域波形描述，也可以用功率谱密度描述。如图5
图5 随机载荷信号的时域波形描述和频域PSD描述
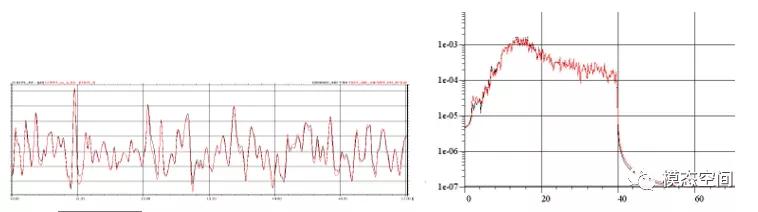
时域随机信号疲劳损伤谱的计算方法与上述正弦信号的计算方法并无本质差别。将时域随机信号施加于一固有频率为f0，阻尼比为ξ 的线性单自由度系统，我们可以用瞬态动力学方法计算出系统的相对位移z(t)。
对z(t)进行雨流法计数，计算出每个幅值Zi所对应的循环次数ni。然后利用Miner线性损伤累积准则，计算出单自由度系统的疲劳损伤值
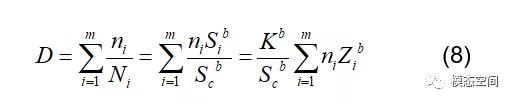
以固有频率f0为横轴，疲劳损伤值D为纵轴绘制曲线D(f0)，就是该时域随机信号的疲劳损伤谱。
耐久性随机载荷通常持续时间很长，考虑整个时域波形会导致较大的计算量。幸运的是，耐久性随机载荷通常都是平稳的和各态历经的，这样我们只需要截取一个代表性时间段Ts的波形，计算该段载荷所造成的损伤DTs(f0)，然后用下式得到总持续时间Ttotal所对应的损伤D(f0)
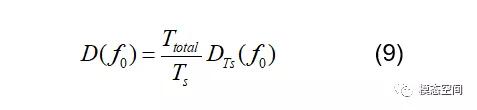
对于PSD形式的随机载荷信号，则可以采用频域疲劳理论来计算单自由度系统的损伤值D(f0)。
1.首先根据输入载荷PSD GL(f)，计算出单自由线性系统相对位移的PSDGz(f)，即
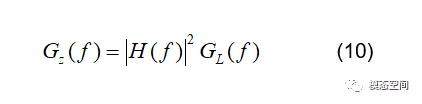
2.因为相对位移与系统应力成比例关系，所以可进一步得到单自由度系统的应力PSD GS(f)
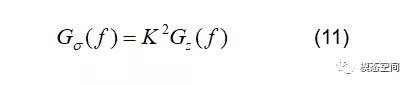
3.得到应力PSD后，可计算出应力PSD的力矩mn、穿零概率期望E[0]、峰值概率期望E[0]和不规则因子γ等数值。
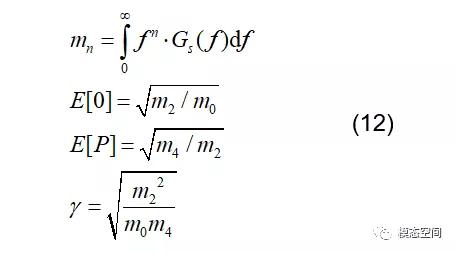
5.得到概率密度函数p(S)后，则在时间段T内，应力幅度在S和S+dS之间的循环次数为
有多种频域失效模型可供选择，区别只在于概率密度函数p(S)的计算方法不同。实际操作中，经常使用Lalanne模型来计算耐久性随机载荷的疲劳损伤谱，如下式
其中函数erf的定义如下：
05 结语
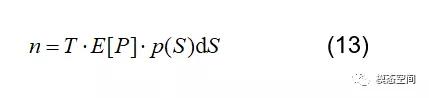
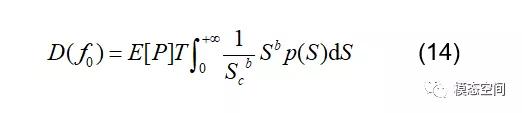
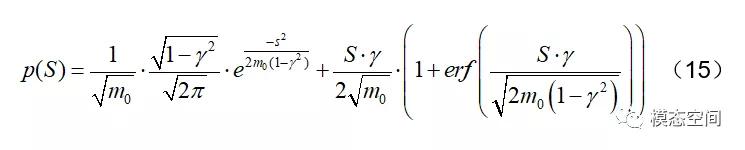
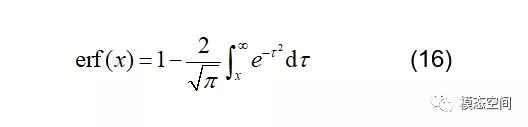
疲劳损伤谱的计算过程中只考虑了理想化的单自由度系统，并不涉及到载荷信号实际所作用的结构。换言之，对于某个指定的载荷信号，其疲劳损伤谱就只与我们设定的四个常数有关，与载荷所作用的具体结构和产品无关。
疲劳损伤谱的算法实质上借鉴了冲击响应谱和伪损伤值的算法。它模仿冲击响应谱，将载荷施加于一系列单自由度线性系统，然后计算单自由度系统的响应。得到单自由度系统的相对位移后，又模仿伪损伤值算法，利用标准SN曲线和Miner线性准则进行疲劳损伤计算。
疲劳损伤谱描述的是单自由度系统的损伤值随其固有频率的变化，能体现载荷信号中不同频率成分的贡献。而伪损伤值只是一个单一数值。所以疲劳损伤谱相比伪损伤值能提供更多的信息，对载荷的评价更为精细。
疲劳损伤谱常用于加速度载荷，但实际上它对于力、力矩、位移、速度等载荷同样适用。伪损伤值是直接分析载荷信号的波形，其结果通常会夸大高频成分的贡献，所以很多情况下要对载荷进行低通滤波处理。而疲劳损伤谱并不是直接分析载荷信号，而是对单自由度系统的响应进行计算，能够比较合理的评估高频成分的贡献，无需对信号进行滤波处理。
疲劳损伤谱在国内应用较少，但在国外已用于道路试验用户关联和台架试验加速，取得了良好的效果。有关疲劳损伤谱的工程应用，后续将有文章进行讨论。
广告 
广告
广告
最新资讯
-
生产制造 | 产品加工-EDGECAM 高效自动编程
2024-12-27 17:39
-
设计仿真 | Adams_Controls变拓扑分析
2024-12-27 17:39
-
设计仿真 | Digimat用于碰撞、冲击模拟热塑
2024-12-27 17:38
-
设计仿真 | 海克斯康 MSC Nastran 助力沃尔
2024-12-27 17:37
-
CAERI风洞丨整车环境风洞风雨场探究
2024-12-27 17:16
广告
广告
