广告
基于阶次分析的永磁同步电机噪声源识别
2020-03-14 00:31:23· 来源：EDC电驱未来 作者：林福
昨天点击上方右侧EDC电驱未来可订阅哦！下载方式，详见文末！！！本文首先进行了电机噪声试验，根据不同的阶次特征对主要噪声进行了分类。其次针对台架的机械噪
本文首先进行了电机噪声试验，根据不同的阶次特征对主要噪声进行了分类。其次针对台架的机械噪声源进行了分析，并且探讨了不同影响因素（包括电流谐波和转子动态偏心）下的径向力波特征，通过实际安装条件下的电机模态分析识别出了共振区的模态参数。综合不同影响因素下的机械和电磁激励特征分析以及电机模态分析对主要的阶次噪声和共振噪声来源进行了解释，并且分析了各影响因素产生的噪声对总体噪声的贡献。
1 永磁同步电机噪声试验及分析
噪声测试的对象为一6极9槽分数槽集中绕组永磁同步电机，定转子结构如图1所示。测试台架示意图如图2所示，电机转轴通过联轴器与测功机连接，通过2个夹紧片将定子固定在定位圈内，转轴两端通过轴承支撑在轴承座上，通过隔音罩将测功机和联轴器的噪声隔离。
图1 永磁同步电机定转子结构
Fig.1 Stator and rotor structure of permanent magnet synchronous motor
图2 电机噪声测试台架示意图
Fig.2 Schematic diagram of motor noise test bench
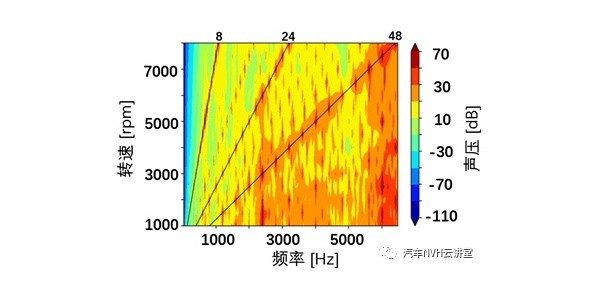
噪声测点布置在离电机中心正上方35 cm处，测试电机的近场噪声。电机噪声源的识别可以采用稳定工况下的噪声信号，也可以选择加速工况下的噪声信号。图3所示为电机在额定运行工况下噪声频谱，对应的转速为3 600 r/min，负载扭矩为2.7 N·m。加速条件下的噪声信号采集过程如下：先将电机稳定在1 500 r/min，然后匀加速上升到5 000 r/min，通过LMS SCADAS III数采系统采集加速过程中的噪声时域信号，并对其进行短时傅里叶变换，结果如图4所示。通过对比图3和图4可以看出，加速条件下的电机噪声包含所有稳态噪声的阶次，而且相比稳态信号具有2个优点：1）由图4可以发现有些噪声阶次随着转速升高频率向右移动，而有些噪声阶次则以9 000 Hz为中心向两侧移动，当两者频率重合时，采用稳态下的噪声信号进行声源识别容易混淆两种阶次特征；2）加速条件下的噪声信号更易于观测电机的共振区域。因此本文采用加速条件下的噪声信号对电机噪声来源进行识别。
图3 额定工况下的电机噪声A计权声压级
Fig.3 Frequency spectrum of A-weighted sound pressure level of motor noise under rated condition
注：fc为开关频率，Hz；f0为电流基频，Hz；图中数字表示阶次，下同。
Note: fcis the switching frequency, Hz; f0is the fundamental current frequency, Hz; The number denotes the order, the same below.
图4 加速过程中的电机噪声A计权声压级时频图
Fig.4 Time-frequency map of A-weighted sound pressure level of motor noise in acceleration process
根据图4可以将主要的噪声分为以下5类：
1）分数阶噪声：幅值比较大的包括3.2和4.8阶噪声。
2）6k阶噪声：主要包括6、12、18、24、30、36、42、48、54、60、66、72和78阶噪声。
3）6k±1和6k±2阶噪声：主要包括7、8、17、19、20、35、37、38和43阶噪声。
4）以开关频率fc(9 000 Hz)为中心的噪声阶次：主要包括fc、fc±f0、fc±2f0、fc±3f0、fc±5f0、fc±7f0和fc±9f0等。
5）共振噪声：比较明显的共振区域包括 1 180～1 389、2 411～2 822和3 200～3 425 Hz，该“固定”区域的噪声来源于2）和3）中的阶次噪声对应的激励频率靠近结构模态频率引起的共振而辐射的噪声，可以看到该部分噪声的能量较高，对电机噪声的贡献是最主要的。
下面通过机械和电磁激励分析并且结合电机模态分析对上述5类噪声的来源进行解释。
2 滚动轴承的噪声阶次特征分析
滚动轴承产生的噪声阶次特征与轴承的尺寸和滚珠的个数相关，图5所示为滚动轴承模型。
图5 滚动轴承模型
Fig.5 Rolling bearing model
注：D为轴承节径，mm；β为接触角，rad；db为滚珠直径，mm。
Note: D is the pitch diameter, mm; β is the contact angle, rad; dbis the ball diameter, mm.
较常见的轴承噪声阶次包括内外圈的通过频率，为滚珠通过内滚道和外滚道时产生的冲击特征，由文献[7]可得内圈和外圈的通过频率分别为
式中fir、for为轴承内外圈的通过频率，Hz；Nb为滚珠个数；fr为转轴的转动频率，Hz。D为轴承节径，mm；β为接触角，rad；db为滚珠直径，mm。台架中所用到的轴承为8个滚珠，对应的轴承的内外圈通过频率分别为4.8阶和3.2阶，因此测得分数阶噪声来源于台架的滚动轴承。
3 不同影响因素下的电磁激励阶次特征分析
3.1 理想条件下的电磁力阶次特征
理想条件指的是电机不发生偏心，三相电流为正弦波。对于永磁同步电机而言，由麦克斯韦应力张量法可推导引起电机电磁噪声的径向力波，即
式中Pr表示理想条件下引起电机电磁噪声的径向力波，N/m2；brs表示径向气隙磁密，T；μ0为真空磁导率，H/m。
在永磁同步电机中，气隙磁场包括永磁体产生的磁场和绕组通电后产生的电枢磁场，两者都为旋转磁场，同时具有随空间分布和随时间变化的特征，而定子开槽只影响气隙磁场的空间分布，通常引入气隙比磁导对磁场进行修正。对于本文研究的6极9槽电机，由于其为表贴式电机，有效气隙长度较大，磁路一般不饱和，因此通过将永磁体磁密和电枢磁密线性叠加再乘以考虑开槽效应的气隙比磁导可以得到气隙磁密，即
式中Br_mag， Br_arm和λa分别表示径向永磁体磁密、径向电枢磁密和气隙比磁导，三者可通过傅里叶级数进行表示
式中θ表示空间角度，t表示时间，p表示极对数，Qs为定子槽数，Nt为电机的空间周期数。Bmn、Bav和λaμ分别表示永磁体磁密、电枢磁密和气隙比磁导谐波幅值。sv表示空间vNt次电枢磁密谐波的旋转方向，当其与转子旋转方向相同时为1，相反时为-1。
由式（7）可知，开槽不影响磁密的频率特征，因此在推导径向力波阶次特征时忽略开槽的影响，结合式（3）～（6）可以得到不考虑开槽效应的径向力波，展开后得到
由于 sv、sv1和 sv2只能取±1，由式（8）可知理想条件下的径向力波的频率特征为电流基频的偶数倍，即为极数的整数倍阶，对于6极电机而言，即为6k阶(k为整数)。因此测得的6、12、18、24、30、36、42、48、54、60、66、72和78阶噪声主要来源于永磁体磁密和电流基波磁密作用下的电磁激励。
3.2 电流谐波引起的电磁力阶次特征
目前的调速永磁电机大多采用变频器供电，变频器供电下电流波形不再是理想的正弦波，电流中存在着大量的电流谐波，电流谐波的存在使得电磁力频率成分更加丰富，也增加了结构共振的可能性。在噪声试验测试过程中通过电流钳对电机相电流进行监测，图6所示为将测试的加速过程中的A相电流通过短时傅里叶变换得到的结果，从图中可以看出电机的电流谐波可以归为两类，一种是电流基频f0的(6k±1)倍电流谐波，随着转速的升高在时频图中朝右移动，幅值较大的包括5、7、11和13次谐波。另一种电流谐波以开关频率fc为中心对称分布，包括fc，fc±f0，fc±2f0，fc±4f0和fc±8f0等。
假设电流谐波的频率为fh，相位为θh，其产生的电枢磁密可表示为
式中h为根据电流频谱得到的某一电流谐波，Bahv为其产生的空间vNt次电枢磁密幅值。
电流谐波对径向力波的贡献主要来源于其产生的磁场与永磁体磁场的相互作用，因此电流谐波产生的额外径向力波可表示为
由上式可知频率为 fh的电流谐波产生的径向力波的频率特征为nf0±fh。由于在永磁体磁密中，基波磁密(n=1)的幅值最大，若只考虑永磁体基波磁密的作用，可得到图6中的电流谐波产生的径向力波的主要阶次，如表 1所示。
图6 加速条件下的A相电流时频图
Fig.6 Time-frequency diagram of A phase current in acceleration process
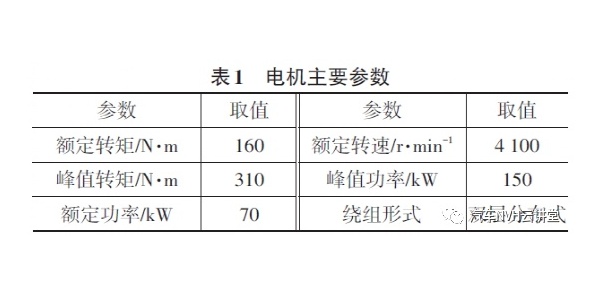
表1 电流谐波产生的主要径向力波阶次
Table 1 Radial force order due to current harmonics
由表1可以看出，对于(6k±1)f0类型的电流谐波，其产生的径向力波的频率特征也为电流基频的偶数倍，与理想条件下的径向力波的频率特征重合，因此不能通过振动或者噪声信号反推该类电流谐波的存在。而对于形如fc±hf0类型的开关频率附近的电流谐波，其产生的径向力波的特征满足 fc±(h±1)f0，可以通过振动或噪声信号反推对应的电流谐波阶次。
通过表1可以发现，图4中的12(4f0)、18(6f0)、24(8f0)、30(10f0)和36(12f0)阶等6k阶噪声除了受永磁体磁密和电流基波磁密作用产生的电磁激励外，还来源于(6k±1)f0类型电流谐波的作用。而 fc、fc±f0、fc±2f0、fc±3f0、fc±5f0、fc±7f0和 fc±9f0等形式的噪声来源于开关频率附近电流谐波的作用，其对应的电流谐波都可以在表 1中找到。可以发现满足fc±af0(a为整数)的噪声，其可能的电流谐波阶次为fc±(a±1)f0。
3.3 转子动态偏心引起的电磁力特征
第三，提高企业员工的工作能力与风险意识。企业员工具有良好的风险意识，可以提高企业内部的控制管理效率，减少各种风险的出现。同时企业员工具备足够的工作能力，可以使其有效的对会计政策、今后阶段相应的财务风险问题进行解读，及时制定合理的风险防范措施，减少各项管理风险。
图7 转子动态偏心示意图
Fig.7 Schematic diagram of rotor dynamic eccentricity
注：ωr=2πfr，为转动角频率，rad/s；fr为转动频率，Hz；ed为偏心距离，mm。
Note: ωris the rotation frequency and equals to 2πfr, rad/s; fris the rotation frequency, Hz; edis the eccentricity length, mm.
从图7中可以看出，电机发生动态偏心时，气隙长度随时间发生变化，因此动态偏心会引起额外频率的径向力波，其对气隙磁密的影响通常通过引入偏心修正系数进行考虑，表达式如下
从图7中可以看出，电机发生动态偏心时，气隙长度随时间发生变化，因此动态偏心会引起额外频率的径向力波，其对气隙磁密的影响通常通过引入偏心修正系数进行考虑，表达式如下
式中λd为偏心修正系数；εd=ed/g'，其中ed为偏心量，mm；g′为有效气隙长度，mm。
令气隙中空气的长度为 g，mm。对于内置式电机g′=g，而对于表贴式永磁电机g′=g+hm/ur，其中hm为永磁体厚度，mm；ur为永磁体相对磁导率。因此当电机偏心量相同时，内置式永磁电机的气隙磁密的畸变大于表贴式电机，即内置式电机对偏心更加敏感。
电机中的径向力波可以表示成一系列不同空间阶数和频率的力波的叠加，即式（8）可表示为m
式中m表示径向力波的空间阶数，Am、fm和φm分别表示m阶径向力波的幅值、频率和相位。
通过气隙磁密修正系数可以得到动态偏心下的径向力波
可以看出转子动态偏心会引起额外的空间阶数的径向力波，由于电机振动噪声对径向力波的空间阶数变化较为敏感，因此转子偏心引入空间低阶的径向力波，会严重加剧电机的振动和噪声。此外动态偏心还会引起额外的径向力波频率成分，在原有的2pk阶两侧出现2pk±1 和2pk±2阶力波分量。对于6极电机而言，转子动态偏心产生的径向力波频率特征为6k±1和6k±2阶。因此图4所示的7、8、17、19、20、35、37、38和43阶噪声来源于转子动态偏心，而且从图中可以看出虽然该部分激励幅值较小，但在靠近结构模态频率处仍能产生较大的噪声。
4 电机固有特性分析
由图4可以看出加速过程中的噪声时频图中存在明显的“固定区域”的噪声，其来源于电磁力频率靠近结构模态频率时引起的结构共振产生的声辐射。为了识别出这些区域对应的模态需要对电机进行模态分析，以求进一步从结构优化角度进行减振降噪。
4.1 定子有限元建模及试验验证
在图2所示的定子安装中，定子固定在定位圈内，难以在定子表面布置加速度传感器，因此无法进行定子实际安装条件下的定子模态试验。本文首先通过自由条件下的定子铁芯和定子总成的模态试验来验证建立的定子有限元模型，再模拟定子在台架中的约束来识别定子在实际安装条件下的定子模态参数。
定子铁芯在结构上由硅钢片沿轴向叠压而成，而且在定子齿上绕有线圈，由于在有限元建模中不可能按照实际的结构对定子铁芯和绕线进行建模，因此需要建立起对应的定子铁芯和绕组的等效模型，等效模型的准确性通过模态试验进行验证。
为了分别验证定子铁芯和绕组建模的准确性，分别进行了定子铁芯和定子总成的模态试验，如图8所示。在试验过程中，沿定子周向均匀布置12个振动测点，沿轴向布置两圈，通过激振器施加宽频激励信号，并且由力传感器测量激振信号，最终可以获取激振点到振动测点间的频响函数，用于模态参数识别。为了减小传感器带来的误差，进行分批测量，每次只测量激振点到 3个振动测点的频响函数。图9所示为对应的定子有限元模型，其中定子铁芯为实体模型，而绕组等效模型的选择则考虑到该6极9槽电机为分数槽集中绕组电机，一个线圈绕在一个齿上，端部绕组较短，因此忽略端部的建模，只考虑绕组在槽内的部分。
图8 定子模态试验
Fig.8 Modal test of stator
图9 定子有限元模型
Fig.9 Finite element model of stator
由实际的定子铁芯和绕组结构可知该等效模型需要考虑材料的各向异性。由于电磁力沿轴向分布基本一致，因此电机的轴向一致模态（变形沿轴向一致）对电磁振动和噪声的贡献是最大的，所以在模型等效时以轴向一致模态频率为目标，而忽略反对称模态。在材料参数上，由轴向一致的模态振型的运动方向可知，x，y方向上的杨氏模量Ex，Ey以及xy平面内的剪切模量Gxy对这些模态频率的影响是最大的。通过模态试验测得的定子铁芯和定子总成的模态频率对铁芯和绕组的Ex，Ey和Gxy进行修正，使得定子的有限元仿真模态频率靠近实测模态频率。图10为试验和有限元分析得到的模态振型，图10a中的点即为模态试验中的振动测点。表 2所示为等效后的定子频率与实测模态频率的对比，可以看到等效后的定子铁芯和定子总成的模态频率与实测频率的相对误差分别在1%和5%以内，满足工程误差的要求，说明了该定子有限元建模的准确性，可以用来进一步预测约束条件下的定子模态参数。
图10 定子试验和有限元模态振型对比
Fig.10 Contrast of tested and simulated mode vibration of stator
表2 定子有限元模态与试验模态频率对比
Table 2 Contrast of simulated and tested mode frequency of stator
4.2 定子约束模态分析
为了预测定子在实际安装条件下的定子模态参数，按照台架安装下的约束对定子进行了模态分析，由于定子在两个圆弧边上通过夹紧片夹紧，因此通过在定子铁芯外表面与夹紧片的接触处施加固定约束来模拟定子在台架中的安装条件。图11所示为约束条件下的定子有限元模态分析得到的轴向一致的模态振型及对应的频率（为了更清楚的观察振型，图中隐藏了绕组部分）。可以看出图11所示的模态频率处在图4中的1 180～1 38 9、2 411～2 822和3 200～3 425 Hz 3个共振区域中，为共振对应的定子模态，当电磁力频率靠近该三处模态频率时产生较大的电磁振动和噪声。
图11 定子约束模态振型和频率
Fig.11 Restrained modal vibration and frequency of stator
注：图中隐藏了绕组部分。
Note: Winding section is hidden in the graph.
4.3 转子模态分析
转轴不对中、不平衡主要引起2阶以内的机械激励，而在电磁激励方面，对于本文的6极9槽电机，发生转子动态偏心时会产生 1阶的不平衡磁拉力。综合两方面来源可知，引起转轴弹性变形的主要激励源在2阶以内，在达到最高转速5 00 0 r/min时，频率为167 Hz。进一步建立转子的有限元模型，对其进行有限元模态分析，图12所示为转子前两阶模态参数，可以看出转子的模态频率距离激励频率较远，电机在整个转速运行范围内并没有激起转子的共振，因此在图4中并没有找到转子模态频率对应的共振区域。
注：激励频率为167 Hz。
Note: Excitation frequency is 167 Hz.
从图4的噪声时频图可以看出对噪声贡献最大的为图11所示的定子模态，但仍有其他噪声能量相对较低的共振区域未得到解释，例如：1 900、4 300和 5 200 Hz附近的区域共振。在这些区域内并没有找到对应的定转子模态频率，推测其来源于电机夹具、台架本身的固有特性。
图13 不同转速下各噪声来源对总声压级(A计权)的贡献
Fig.13 Contribution of each source to the overall sound pressure level (A-weighted) in the whole speed range
注：图中6k阶噪声对应的激励来源包含两部分：1) 理想条件下的电磁力；2) (6k±1)f0次低阶电流谐波引起的电磁力。
Note: The corresponding force of the 6k-th order noise in the figure includes two sources: 1) the electromangetic force under the ideal case; and 2) the electromangetic force resulting from current harmonics with the (6k±1)f0-th orders.
5 噪声贡献量分析
通过LMS Test.lab软件可以提取图4所示的各阶次噪声，并且根据噪声的分类将相同影响因素产生的阶次噪声叠加后可以得到各影响因素产生的噪声，如图13所示。值得注意的是，根据不同影响因素下的电磁激励特征分析，图中的6k阶噪声包含两部分来源：1）理想条件下的电磁力；2）(6k±1)f0次低阶电流谐波引起的电磁力。由于这两部分来源阶次特征重合在一起，通过噪声信号不能区分。
从图中可以看出随着转速的上升，总声级呈现上升趋势。其中永磁体磁场和(6k±1)f0次电流谐波产生的磁场相互作用导致的6k阶噪声以及开关频率附近的电流谐波导致的高频噪声对总体噪声的贡献最大。转子动态偏心产生的阶次噪声取决于偏心阶次同结构模态的靠近程度，从图4可以看出当电机运行在4 400 r/min附近时，动态偏心产生的17、19和20阶电磁力靠近定子1 267 Hz模态频率，而35、37和38阶电磁力靠近定子2 460 Hz模态频率，因此在该转速下，动态偏心产生的阶次噪声达到最大。滚动轴承产生的分数阶噪声对总体噪声的贡献较小，然而其随转速的升高逐渐增大，在高速时，对总体噪声仍有一定的贡献。
6 结 论
1）低阶次的电流谐波产生的电磁激励与理想条件下的电磁力特征重合，所贡献的噪声阶次都为极数的整数倍；而以开关频率为中心的高频电流谐波则会引起开关频率附近的边频电磁噪声。
2）转子动态偏心在原有的极数的整数倍阶次噪声两侧引起额外的±1和±2阶的边频阶次噪声，贡献的比较明显的噪声阶次主要来源于其产生的电磁力通过结构模态时产生的结构共振导致。
3）定子振型沿轴向分布一致的模态对电磁振动和噪声的贡献是最主要的，通过考虑铁芯和绕组材料的各向异性可以建立较为准确的定子结构模型。
4）针对本文的6极9槽电机，通过各影响因素的噪声贡献量分析可以发现，永磁体磁场和低阶次电流谐波产生的磁场相互作用导致的极数的整数倍阶噪声以及开关频率附近的电流谐波导致的高频噪声对总体噪声的贡献最大，动态偏心产生的噪声次之，滚动轴承产生的噪声贡献量最小。
广告 
广告
最新资讯
-
荷兰Zepp氢燃料电池卡车-Europa
2024-12-22 10:13
-
NCACFE -车队油耗经济性报告（2024版）
2024-12-22 10:11
-
R54法规对商用车轮胎的要求（上）
2024-12-22 10:10
-
蔚来ET9数字架构解析
2024-12-22 09:53
-
4G/5G网络新时代的高效紧急呼叫系统NG-eCal
2024-12-20 22:33
广告
广告
