广告
同轴直联电驱桥传动系统动态特性研究
2020-04-13 22:35:22· 来源：EDC电驱未来
1 引言以纯电驱动汽车同轴直联行星轮系为研究对象，应用集中参数理论建立了系统的动力学模型，对不同输入转数下系统的动态响应进行计算及分析，以得到整个传动系
1 引言
以纯电驱动汽车同轴直联行星轮系为研究对象，应用集中参数理论建立了系统的动力学模型，对不同输入转数下系统的动态响应进行计算及分析，以得到整个传动系统的动态特性。
2 传动系统动力学模型建立
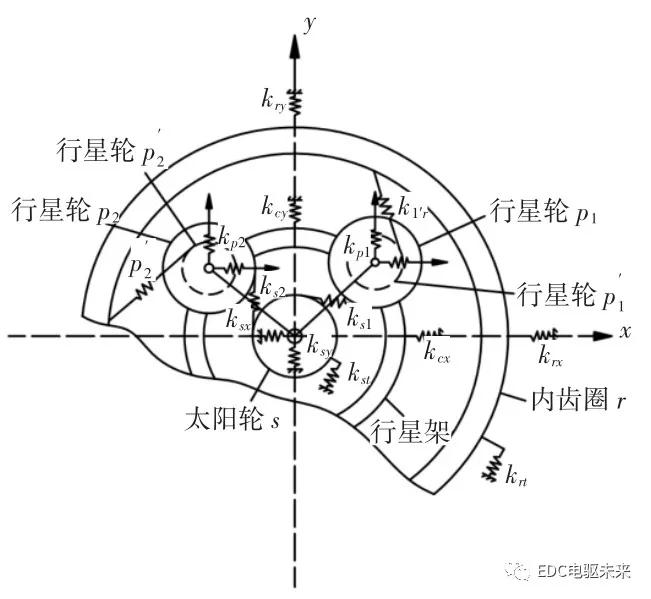
本研究采用同轴直联纯电驱动车桥为研究对象，动力学模型，如图1所示。纯电驱动车桥采用行星减速机构，驱动电机壳体与车桥壳体共用，驱动电机轴与行星减速机构太阳轮一体化设计，从而实现输入与输出的同轴直联与深度集成。这种设计能够有效地解决电动汽车偏载、重量重、体积大与能耗高等问题，并改善行驶平顺性。
图1 行星轮系动力学模型
Fig.1 Dynamic Model of the Planetary Gear Set
图中：ksx，kcx，krx—太阳轮、行星架与内齿圈的 x 向刚度；ksy，kcy，kry—太阳轮、行星架、内齿圈的 y向刚度；kst，krt—太阳轮与内齿圈的切向刚度；kp1，kp2—两行星轮径向刚度；ks1，ks2—太阳轮与两行星轮的啮合刚度；k1’r，k2’r—两行星轮与内齿圈的啮合刚度。设行星轮个数为N，则太阳轮与行星轮n（n=1，2，3，…，N）啮合部位的局部放大图，如图 2 所示。
图2 啮合部位局部放大图
Fig.2 Partial Enlarged Drawing of the Meshing Position
图中：φn—行星轮n中心和太阳轮中心连线与x轴正向的夹角；αsn—太阳轮与行星轮n的啮合角；ωs与ωn—太阳轮与行星轮n的转数；rs与rn—太阳轮与行星轮n的基圆半径；xs与xn—太阳轮与行星轮n在x方向上的位移；ys与yn—太阳轮与行星轮n在y方向上的位移。设定ksn受压为正方向，则太阳轮与行星轮n之间相对位移在啮合线上投影为：
同理，行星轮n’与内齿圈相对位移沿啮合线投影为：
式中：xn′与 xr—行星轮 n′与内齿圈的 x 方向位移；αn′r—行星轮 n′与内齿圈的啮合角；yn′与yr—行星轮n′与内齿圈的y方向位移；ωn′与 rn′—行星轮 n′的转数与基圆半径；ωr与 rr—内齿圈的转数与基圆半径。
行星轮n与行星架间相对位移在xn，yn坐标轴及行星架扭转方向上投影为：
式中：xc，yc—行星架 x，y方向位移；ωc—行星架转数；rc—行星轮与太阳轮中心距。
3 系统运动方程建立
设输入转矩为Ts，输出转矩为Tc。忽略系统元件与结构件之间摩擦带来的影响，建立系统运动微分方程为：
式中：ms—太阳轮质量；csx—太阳轮x向阻尼；csy—太阳轮y向阻尼；csn—太阳轮与行星轮n之间啮合阻尼；Js—太阳轮转动惯量；θs—太阳轮转角；以顺时针为正方向；cst—太阳轮切向阻尼。mn与 mn′—行星轮 n 与 n′的质量；cn′r—行星轮 n 与内齿圈之间啮合阻尼；cpn—行星轮n径向阻尼；Jn与Jn′—行星轮n与n′的转动惯量；θn—行星轮n的转角。mc—行星架质量；ccx—行星架的x向阻尼；ccy—行星架的y向阻尼；Jc—行星架转动惯量；θc—行星架转角。mr—内齿圈质量；crx—内齿圈x向阻尼；cry—内齿圈y向阻尼；Jr—内齿圈转动惯量；θr—内齿圈转角；crt—内齿圈切向阻尼。
4 系统动态特性计算
将式（4）-式（7）统筹整理成矩阵形式：MX¨+CX˙+KX-T=0（8）式中：M—系统质量矩阵；C—阻尼矩阵；K—刚度矩阵；T—转矩矩
阵。应用Runge-Kutta方法对方程组进行求解，并定义系统
式中：xi peak—构件i振动位移峰值；ximax—构件i在当前转数下振动位移最大值；xi min—构件i在当前转数下振动位移最小值。各构件在不同转数下的径向振动位移峰值计算结果，如图4所示。
图3 各构件径向振动位移峰值
Fig.3 Radial Displacement Peak Value of the Components
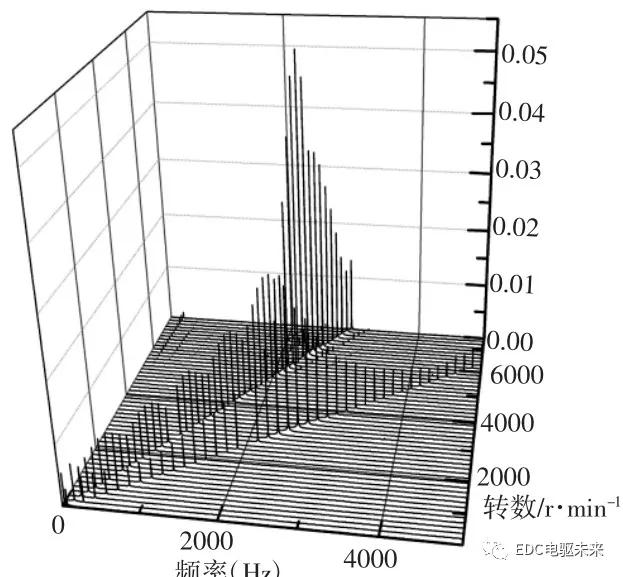
图3中，点划线所示为行星架径向位移随转数变化趋势，虚线所示为太阳轮径向位移随转数变化趋势，细实线所示为内齿圈径向位移随转数变化趋势，粗实线所示为行星轮径向位移随转数变化趋势。可以看出，各结构件径向位移峰值随转数变化趋势大致相同，只是变化幅度有较大区别。各结构件振动位移峰值在计算频段内呈现双峰特征，分别对应系统两阶临界转数。在转数达到二阶临界转数之前，行星架径向振动要大于太阳轮径向振动，而在转数达到二阶临界转数之后，太阳轮径向振动要大于行星架径向振动。选取图4中行星架径向位移作为研究对象。为获得不同转数下行星架径向位移的频域特性，对从（150～7500）r/min，转数步长Δn=150r/min取50组不同转数进行行星架径向振动计算，并将结果做FFT处理，得到结果，如图4所示。
图4不同转数下行星架径向振动频域特性
Fig.4 Radial Vibration Frequency Characteristics of the Planet Carrier Under Different Revolutions
图4 中，行星架径向振动频域结果表现为两个峰值，随着输入转数上升，两峰值频率均呈现线性增高趋势。较低峰值频率对应行星轮n′与内齿圈啮合频率fm1，而较高峰值频率对应太阳轮与行星轮n的啮合频率fm2。fm1与fm2对应峰值频率对总体振动贡献情况随转数变化规律，如图5所示。
图5峰值频率对总体振动贡献随转数变化情况
Fig.5 Changes of Contribution of Peak Frequency to Total Vibration with Rotation Speed
图5 中，实线所示为fm1对总体振动贡献情况，虚线所示为fm2对总体振动贡献情况。可以看出，两峰值频率对总体振动贡献在低频段比较接近，在中频段fm2对应峰值频率对总体振动贡献增大较快，随后迅速衰减。在大部分频段内fm1对总体振动贡献较大，这一点在高频段尤为明显。这说明当输入转数发生变化时，行星轮n′与内齿圈之间的啮合振动对行星架影响随转数上升呈逐步增长趋势，而太阳轮与行星轮n之间的啮合振动对行星架影响变化幅度较小并随转数上升呈先上升后迅速下降趋势。这是由于行星轮刚度较小，行星轮n′与内齿圈之间啮合刚度kn′r小于太阳轮与行星轮n之间啮合刚度ksn，啮合刚度较小的路径对输出构件的振动情况影响更大。此外，随着输入转数的升高，对系统动态特性产生影响的相关频率朝高频方向移动，这一结果对电动车桥进一步的隔振研究具有重要意义。
5 结论
建立了电动车桥同轴直联行星轮系模型，并使用Runge-Kutta方法进行求解，得到了系统在不同输入转数下的动态特性，之后对计算结果进行峰值计算与时频特性分析，得到以下结论：
（1）各构件振动频域结果呈现双峰值，分别对应行星轮与内齿圈啮合频率和太阳轮与行星轮啮合频率，随转数升高峰值频率呈线性升高趋势，啮合刚度较小的路径对输出构件的振动情况影响更大。（2）行星轮与内齿圈啮合频率对整体振动的贡献变化在二阶临界转数前不明显，而在二阶临界转数后明显上升，而后又迅速下降。（3）太阳轮与行星轮的啮合频率对整体振动的贡献变化在一阶临界转数后迅速上升，而后逐渐衰减至不明显。在进一步隔振设计与优化时可根据计算结果避开临界转数，减小传动系统振动对整车振动的影响，提升电动汽车NVH性能。
- 下一篇：纯电动客车AMT换挡策略研究与仿真分析
- 上一篇：德国大众等在无锡设立研发和测试中心
广告
最新资讯
-
国外Rivian和Lucid被认为是特斯拉劲敌，而
2024-05-03 09:26
-
干货丨燃料电池低温特性测试——冷冻解冻循
2024-05-03 09:25
-
特斯拉放弃“一体化压铸”
2024-05-03 08:58
-
纯电动汽车电驱动系统功能安全技术全方位解
2024-05-03 08:54
-
动力电池行业离职率飙升
2024-05-02 17:19
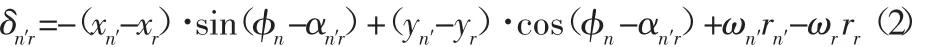
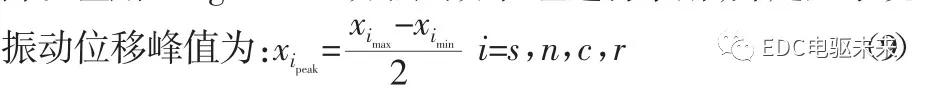
广告
广告
