广告
锂离子电池聚丙烯隔膜变形模式研究
2020-04-15 00:00:07· 来源：汽车安全与轻量化
清华大学周青教授团队，美国麻省理工学院Wierzbicki教授团队以及康涅狄格大学徐弘毅教授团队近期联合针对锂离子电池中的PP隔膜进行了深入的力学研究。利用扫描电
清华大学周青教授团队，美国麻省理工学院Wierzbicki教授团队以及康涅狄格大学徐弘毅教授团队近期联合针对锂离子电池中的PP隔膜进行了深入的力学研究。利用扫描电子显微镜下的隔膜图像，建立了隔膜微尺度的有限元模型，并对隔膜正交各向异性的变形特征进入了深入的仿真和理论的分析。这项工作[1]发表于力学领域重要期刊《极端力学快报》（Extreme Mechanics Letters）。文章由麻省理工学院朱俊儿博士和康涅狄格大学徐弘毅助理教授担任共同通讯作者，第一作者为清华大学的博士研究生潘哲鑫。
目前商业化的锂离子电池中，隔膜是一种用于隔绝电池内正负电极的直接接触的多孔聚合物。对电池性能和安全性有着重大的影响。尽管锂离子电池制造技术日新月异，但由于其较高的性价比，干法制成的聚烯烃（polyolefin）薄膜仍是目前应用最广泛的隔膜之一，例如聚乙烯（polyethylene, PE）、聚丙烯（polypropylene, PP）等。这种材料的独特之处在于其由于制造过程中的干法拉伸工序而具有高度的正交各向异性的微观结构（如图1所示的一种干法PP隔膜）。从图1b中可以看出，原有的隔膜材料在制备过程中在加工方向（MD）上 形成伸长的纤维（fibrils）和孔洞（voids）结构，而未被明显改变的部分则在横向（TD）上形成平行的片层结构（lamellae）。
本研究中的三支团队此前各自均在电池隔膜材料和力学表征方面具有大量积累。例如，MIT团队的张晓伟博士对市场上多种不同的隔膜材料进行了全面的力学实验[2,3]，对隔膜材料的变形机理进行了深入的探究[4-6]，并形成了其博士论文[7]; 清华团队的罗海灵博士对电池隔膜进行了准静态和动态载荷中干、湿两种状态下的力学实验[8,9]，并发现隔膜材料的损伤对电池的安全具有决定性的影响[10]；康州大学团队徐弘毅教授成功搭建了一套基于微观图像创建隔膜材料和力学模型的框架，并有效地预测了隔膜材料力学行为的各向异性[11,12]。本研究是三支团队首次将各自现有的数据和模型进行综合和总结，目的是建立一个可以应用于电池安全和性能研究、满足多种加载工况需求、以及兼顾多尺度力学和物理机理的精确有限元模型。
现有的实验结果显示，由于微观结构和性质的关系，干法制备的PP隔膜在两个正交方向上表现出不同的变形机制。当在MD中以较小的变形拉伸时（图1d），纤维和片层呈串联状态而同时沿相同方向承受载荷。因为原纤维的可扩展性非常有限，所以当变形较大时，应变会集中于在片层中（图1e）。当在TD上拉伸时，纤维不再主要承受载荷，主要变形模式是片层变薄，然后是局部的变形和“颈缩”的发生。此外，实验发现：当工程应变超过60％时，微观结构会进入一种具有失稳的模式（图1g）在宏观上材料会变得透明（图1i，j）。这些不同的变形机制表现在材料的力学性能上，则是两个方向上的拉伸强度大约相差十倍（图1h）。此外，实验中还发现TD加载下薄膜会发生失稳而产生“起皱”现象而MD加载则不会，该独特的力学现象已被MIT的朱俊儿博士等在参考文献[12]中进行了理论层面的分析。
图1 （a) 隔膜微观结构的三维重建 （b) 干法制备过程会使得隔膜具有很强的正交各向异性（c) 俯视图中显示了片层和纤维的差异。当电池在 MD方向(d)-(e) 或TD方向(f)-(g)拉伸时，这种各项异性在应力应变曲线 (h) 就会有明显的差异
在这项研究中，我们通过力学实验后的显微扫描，观测形貌，并结合基于图像的微结构建模技术进行数值模拟，最后通过理论上分析成因。通过实验，仿真和理论分析相结合的方式，我们可以透彻地理解隔膜变形模式的特征。
我们以扫描电子显微镜（SEM）的检查结果为起点来进行材料的微观结构仿真。根据SEM图像，可以确定三个不同的组分：片层，纤维和孔隙。图2描述的是图像处理流程。首先对原始微结构图像（图2a）上进行灰度处理，再基于灰度值和几何特征将像素分类为上述三个组分之一。分类后得到像素化的微结构图像（图2c），再将该图像映射为网格以进行有限元分析。每个元素的物理尺寸是从原始SEM图像的比例尺获得的。
图2 基于图像的微观结构建模过程：利用SEM图像（a）并对其进行特征筛选（b）。然后可以获得一个三相模型（c），其中包括纤维，片层和孔隙（d＆e）。（f）解释纤维形成的微观机理
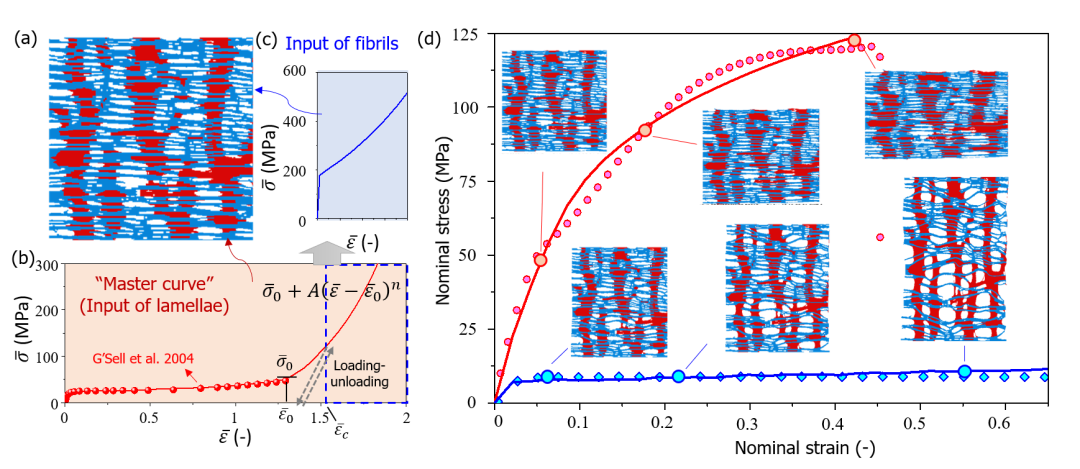
如上所述，我们基于微观结构的模型就将隔膜的单元划分为两种组分：片层（红色）和纤维（蓝色）， 如图3a 所示。二者都需要材料属性的定义作为模型输入。从图2f 的示意图中我们可以看出，这两种不同的材料本质上是聚合物受到外力载荷形成的，可以认为它们只是同一材料在不同加载阶段下的体现。因此，在本研究中，我们通过对两个组分使用同一条“主曲线”来定义。片层被视为该主曲线定义的材料，而纤维是干法拉伸制备过程的产物。因此，通过在卸载过程之后将主曲线加载到特征等效应变来获得硬化曲线。以这种方式，原始的结晶片层变成了拉伸的无定形纤维，因此与材料的物理过程相对应。我们使用主曲线的卸载后重新加载 的过程（图3c）作为纤维的材料输入。
我们从现有聚丙烯材料的文献中获得了这条至关重要的主曲线（图3b）。但由于宏观的聚丙烯材料实验数据往往不能达到较大的变形范围。我们人为地结合曲线尾部地特征进行了一定地延伸，使其范围能够包括 200%的应变。图3d 中展示了优化后MD和TD方向的仿真和实验的对照结果，包括有限元网格变形过程的序列。我们可以发现，我们的模型可以很好地描述材料巨大的各向异性行为。
图3：基于微观结构的力学模型（a）中，片层（b）和纤维（c）的材料输入曲线本质上是同一主曲线（b）的两个部分。主曲线则来自文献中实验数据。（d）图为有限元仿真在两个方向上结果，均有着较高的准确度。虚线对应实验数据；实线对应校准和仿真曲线。
图4a和b分别显示了MD和TD中实验观察结果和数值模拟之间的详细比较。数值模拟几乎可以完美地再现在SEM下观察到的变形模式。此外，我们将此数值模型应用于对角线方向的拉伸，也获得了令人满意的预测。基于这些对已开发的微结构数值模型的可靠验证，我们将该模型随后用于理论分析。
理论分析需要解释的基本问题之一是在TD方向大变形下的上述透明现象。在变形过程中，材料的片层会变薄并产生新的纤维。这样，在不透明的结晶相逐渐变成透明的非晶相，从而在样品中形成可见的宏观透明区域（图1i和j）。但是，尚未完全了解此现象背后的潜在物理机制。是什么导致了图4b中变形模式的变化？一个简单的答案是，该微结构在某个点处从一个均匀的模式分叉到另一个能量较低的模式。
为了阐明其机理，我们采用了隔膜的变形总能量最小的原理，即晶体片层中的应变能和非晶纤维中的应变能之和，如图4d所示。请注意，本研究中的所有能量都是在均质介质构型上定义的，因此，总能量的计算应考虑结晶相和非晶相的重量百分比以及当前的结晶度，由于结晶度也会在变形过程中发生变化，从而会导致能量随着变形非单调的变化。对能量求导取零可以得到此时材料的伸长率为1.59，相应的工程应变为59％，意味着此时会发生从晶相到非晶相的大规模转变，即隔膜透明状态的产生。该理论计算结果，非常接近实验观察到的62.8％。在论文和补充材料中，有更详细的推导。
图4 基于微观结构的隔膜有限元模型可以准确预测MD（a）和TD（b）中的变形模式。（c) (d) 对于TD中的大变形模式，我们提出了材料失稳机制的理论分析
综上所述，我们的实验结果表明，干法分离的PP隔膜在不同方向拉伸时，其变形差异明显。利用微观建模手段，我们建立了一个基于SEM图像的有限元模型来模拟拉伸过程，发现该模型可以成功地再现变形模式并准确预测应力-应变响应。与现有建模工作相比，我们的模型基于材料本身，因此其成功不依赖复杂的标定，几乎所有参数都直接来自实验数据。这一优势使当前模型对于机理研究相对可靠。根据实验和数值结果，我们仔细地对材料的微观结构不稳定性以及在大变形下产生的透明现象进行了理论分析。我们发现隔离膜变成透明的原因有两个方面。一种是指在薄片中产生新纤维的应变局部化，另一种是因为纤维和片层都可以通过变形和整个结构耗散能量能量应该达到最小。我们相信，这种结合了实验，数值计算和理论的研究将为锂离子电池的安全问题提供一个新的理解和表征的途径。
参考文献：
[1] Z Pan, J Zhu, H Xu, T Sedlatschek, X Zhang, W Li, T Gao, Y Xia, & T Wierzbicki, Microstructural deformation patterns of a highly orthotropic polypropylene separator of lithium-ion batteries: Mechanism, model, and theory, Extreme Mechanics Letters (2020) 100705.
https://doi.org/10.1016/j.eml.2020.100705
[2] X Zhang, E Sahraei, & K Wang. Li-ion battery separators, mechanical integrity and failure mechanisms leading to soft and hard internal shorts. Scientific reports 6 (2016): 32578.
https://doi.org/10.1038/srep32578
[3] X Zhang, E Sahraei, & K Wang. Deformation and failure characteristics of four types of lithium-ion battery separators. Journal of Power Sources 327 (2016): 693-701.
https://doi.org/10.1016/j.jpowsour.2016.07.078
[4] X Zhang, J Zhu, & E Sahraei. Degradation of battery separators under charge–discharge cycles. RSC advances 7.88 (2017): 56099-56107.
https://doi.org/10.1039/C7RA11585G
[5] J Zhu, X Zhang, H Luo, & E Sahraei. Investigation of the deformation mechanisms of lithium-ion battery components using in-situ micro tests. Applied Energy 224 (2018): 251-266.
https://doi.org/10.1016/j.apenergy.2018.05.007
[6] J Zhu, X Zhang, & T Wierzbicki. Stretch-induced wrinkling of highly orthotropic thin films. International Journal of Solids and Structures 139 (2018): 238-249.
https://doi.org/10.1016/j.ijsolstr.2018.02.005
[7] X Zhang. Mechanical behavior of shell casing and separator of lithium-ion battery. Ph.D. Thesis. Massachusetts Institute of Technology, 2017.
http://dspace.mit.edu/handle/1721.1/7582
[8] X Jiang, H Luo, Y Xia, & Q Zhou. Mechanical behavior of lithium-ion battery component materials and error sources analysis for test results. SAE International Journal of Materials and Manufacturing 9.3 (2016): 614-621.
https://doi.org/10.4271/2016-01-0400
[9] J Zhu, H Luo, W Li, T Gao, Y Xia, & T Wierzbicki. Mechanism of strengthening of battery resistance under dynamic loading. International Journal of Impact Engineering 131 (2019): 78-84.
https://doi.org/10.1016/j.ijimpeng.2019.05.003
[10] H Luo, Y Xia, & Qing Zhou. Mechanical damage in a lithium-ion pouch cell under indentation loads. Journal of Power Sources 357 (2017): 61-70.
https://doi.org/10.1016/j.jpowsour.2017.04.101
[11] H Xu, M Zhu, J Marcicki, & X G Yang. Mechanical modeling of battery separator based on microstructure image analysis and stochastic characterization. Journal of Power Sources 345 (2017): 137-145.
https://doi.org/10.1016/j.jpowsour.2017.02.002
[12] H Xu, and C Bae. Stochastic 3D microstructure reconstruction and mechanical modeling of anisotropic battery separators. Journal of Power Sources 430 (2019): 67-73.
https://doi.org/10.1016/j.jpowsour.2019.05.021
广告
最新资讯
-
国际化新进程｜德赛西威欧洲新科技园区奠基
2024-05-17 20:15
-
位于上海市内辐射长三角的智能网联功能和性
2024-05-17 20:11
-
2024中国汽车知识产权年会成功召开
2024-05-17 20:05
-
汽车智能座舱声学领域音频全栈测试技术研讨
2024-05-17 20:01
-
HEADlab数采系统十大神奇部件，工作效率Up
2024-05-17 19:58
广告
广告
