广告
基于滑模自抗扰的电制动系统动态负载模拟
2020-05-04 23:10:40· 来源：EDC电驱未来 作者：马瑞海
本文中针对电动汽车制动模式切换及防抱死制动两类动态工况，设计了基于自适应模糊滑模自抗扰（AFSMC＋ESO）的动态加载控制算法。首先，结合感应电机模型，建立车
本文中针对电动汽车制动模式切换及防抱死制动两类动态工况，设计了基于自适应模糊滑模自抗扰（AFSMC＋ESO）的动态加载控制算法。首先，结合感应电机模型，建立车辆和台架机电一体化耦合模型；其次，采用ESO估计系统未建模动态，以新型无抖振AFSMC实现测功机转速跟踪控制；为验证本文提出方法的有效性，与传统PI、ADRC和MPC的负载模拟方法对照；最后，给出两类动态工况下的对比仿真结果，讨论并得出结论。
1 系统模型
1.1 车辆动力学模型
前驱集中式电动汽车电制动系统如图1所示。车用电机为感应电机；忽略系统左右侧差异，电制动力矩经变速器、差速器和左右半轴均匀传递至车轮处。
图1 前驱集中式电动汽车电制动系统
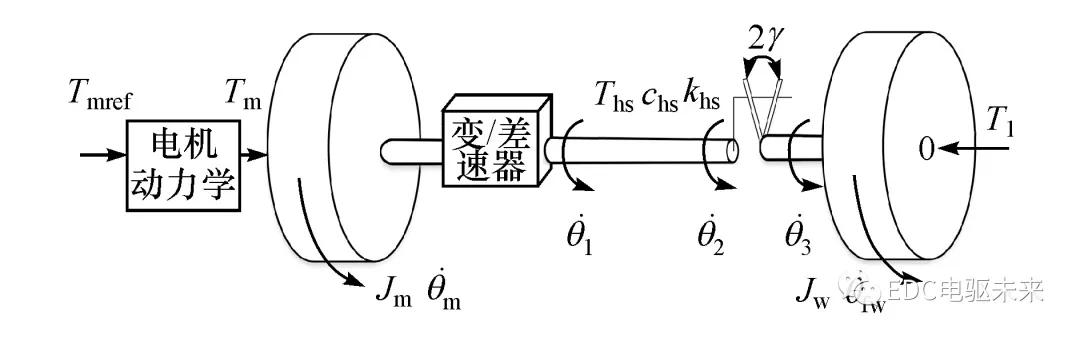
考虑传动环节弹性及非线性齿隙，动力总成模型可简化为双惯量系统［3］，如图2所示。假设传动系弹性主要表现在半轴处，并将传动系齿轮间接触间隙简化为单个齿隙，大小为2γ。
图2 动力总成简化模型
电机参与车辆制动时，电机输出轴至差速器的动力学方程可表示为
式中：T m为电机转矩；T hs为半轴转矩；i0ig为总传动速比；θm为电机输出轴转角；b m为电机阻尼系数；为电机至差速器的等效惯量。可表示为
式中：J m、J1、J2、J3、J diff和J hs分别为电机、减速器输入轴及齿轮、减速器中间轴及齿轮、减速器输出轴及齿轮、差速器和半轴转动惯量。
齿轮两侧未接触时，｜θb｜＜γ，电机与车轮机械解耦，电机力矩无法传递至半轴处；当齿隙两侧齿轮相接触时，齿隙角｜θb｜＝γ。半轴力矩可表示为
式中：k hs为半轴扭转刚度；c hs为半轴扭转阻尼；θs＝θ1-θ3，θb＝θ2-θ3，θ1、θ2和θ3分别为半轴首、末端和车轮转角。齿隙位置θb可表示为
半轴传递至车轮处的制动力矩T fw可表示为
液压制动系统模型参照文献［22］建立，轮胎模型采用Pacejka魔术公式［23］。不考虑道路坡度，驱动轮动力学方程可表示为
式中：J w为车轮转动惯量；θfw为前轮转角；T hf为前轮液压制动力矩；Fx f和Fz f分别为前轮轮胎地面纵向力和法向力；r为车轮半径；f为滚动阻力系数。车身纵向动力学方程可表示为
式中：m为车辆质量；v为车速；F air为空气阻力。
1.2 台架动力学模型
车用电机与测功机刚性共轴连接。沿车用电机至测功机轴向，取顺时针方向为车用电机转速及转矩的正方向，逆时针方向为测功机转速及转矩正方向。因此，台架机械动力学方程可表示为
式中：J＝J m＋J dy，b＝b m＋b dy，J dy和b dy分别为测功机转动惯量和摩擦因数；θdy为测功机转角；T dy为测功机转矩；ΔJ和Δb为模型不确定部分。
1.3 感应电机数学模型
车用电机与加载测功机均为感应电机，dq轴坐标系下感应电机电压、电流、磁链及转矩方程为
式中：id_j、iq_j、ud_j及uq_j分别为dq轴坐标系下定子电流及电压；φrd_j为转子磁链；Tj为电磁转矩；L m_j、L s_j和L r_j分别为定转子等效互感、定子等效自感及转子等效自感；R s_j和R r_j为定转子绕组电阻；ωe_j为同步速；n p_j为极对数；σj为漏感系数。j表示m或dy，指电机或测功机。关键参数见表1。
表1 车辆及台架关键参数
2 测试对象
2.1 正常制动控制
电动汽车正常制动时，电制动系统提供回馈制动力矩协同液压制动力实现制动需求。最大电机制动力矩策略［24］是常见制动力分配方法，根据车辆状态如电机转速及电池荷电状态等实时估计电机所能提供的最大制动力矩T1，同时计算满足驾驶员制动需求下所需前轮制动力矩T2，进一步确定电机回馈制动力矩命令值及液压制动力矩期望值分别为min（T1，T2）和T2-min（T1，T2）。该策略最大化利用电机制动能力，尽可能多的回收车辆动能。
正常制动过程涉及整车能量经济性及驾乘舒适性。为验证制动控制算法有效性，测试台架须能够精确模拟电制动系统动态负载，特别是制动模式切换的高动态过程。
2.2 防抱死制动控制
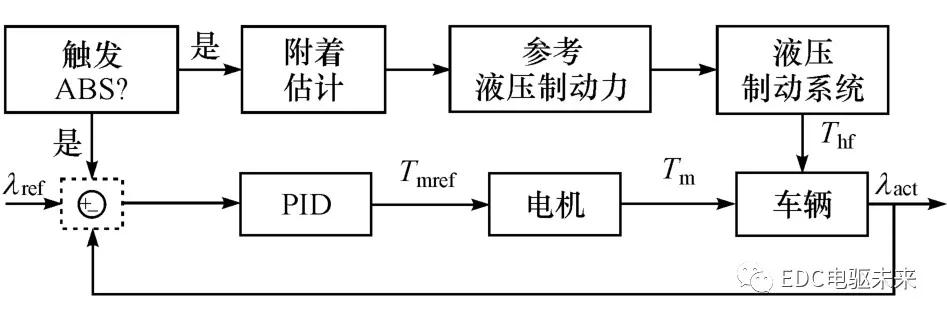
文献［25］中设计了基于PID的机电混合防抱死制动控制方法，见图3。防抱死制动触发后，估计路面附着以确立当前路面所能提供的最大制动力；电制动系统在滑移率PID闭环控制下提供制动力矩，动态调节车轮滑移率稳定于参考值；电机不足以提供足够制动力时，液压制动系统辅助提供稳态力矩。
图3 防抱死制动控制
防抱死制动控制涉及整车安全性，为保证台架测试有效性，负载模拟算法应准确模拟防抱死控制下电制动系统动态负载，特别是防抱死控制性能差、滑移率高频波动的情况。
3 负载模拟方案及控制算法
3.1 台架测试方案
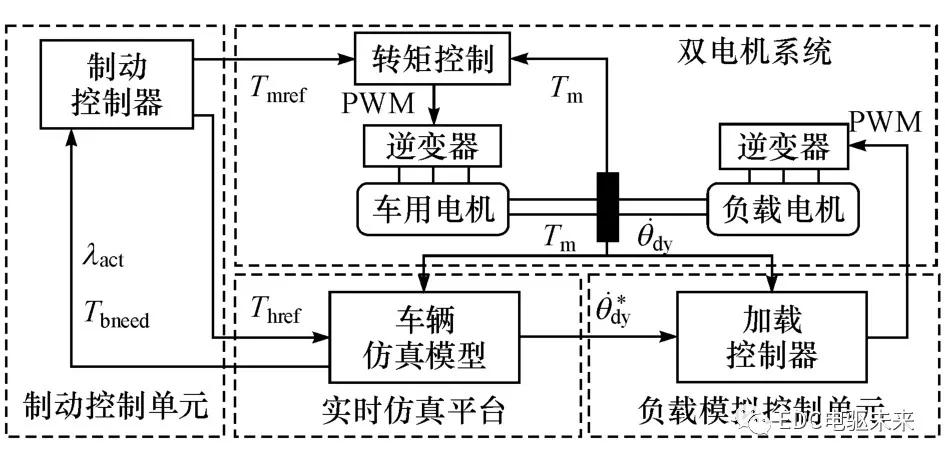
应用完全电模拟的拓扑结构和转速跟踪控制模式模拟待测电制动系统机械负载。负载模拟方案见图4，车辆实时仿真平台、制动控制单元、负载控制单元和双电机系统共同组成台架测试系统。
图4 负载模拟方案
制动控制单元实时监测仿真平台计算的车辆运行状态，依据制动控制算法，控制车用电机对车辆进行制动。负载模拟控制单元控制台架转速实时跟踪仿真平台计算的目标值；跟踪误差越小，负载模拟性能越好，台架测试越有效。
3.2 负载模拟控制算法
为精准模拟传动系弹性及齿隙作用下电制动系统动态负载，本文中设计了自适应模糊滑模自抗扰的负载模拟算法。测功控制系统如图5所示，其中，T m、、i a、i b及i c可测。ESO估计系统未建模动态并前馈补偿，AFSMC控制测功机转速跟踪参考值，q轴电流iq_dy及转子磁链φrd_dy采用PI控制。
3.2.1 扩张状态观测器
图5 测功机控制系统
本文采用非线性ESO估计测功机系统未建模动态及外部扰动，构建如下：
式中：z1、e1分别为转速估计值及估计偏差；z2为扰动估计值；u为控制输入；β1、β2为观测器增益；α1、α2∈［0，1］；δ＞0；fal（e1，α1，δ）为非线性函数。
3.2.2 自适应模糊滑模控制
针对测功机加载控制系统，设计滑模变量如下：
式中：h和c1为正实数；e＝。
为实现控制目标，将系统控制律u设计为
式中：u eq为等效控制律；u r为非线性控制律。
将式（8）代入式（12），得滑模变量1阶导数：
取s＝0，得等效控制律u eq。其中，车用电机力矩及建模不确定部分应用ESO的估计值。
为抑制系统抖振，常采用边界层理论设计非线性控制律，表达式如下：
式中k（t）为控制增益，且k（t）＞Δd，其中Δd为观测器扰动估计偏差Δd＝-z2-（T m＋Δf）／J。
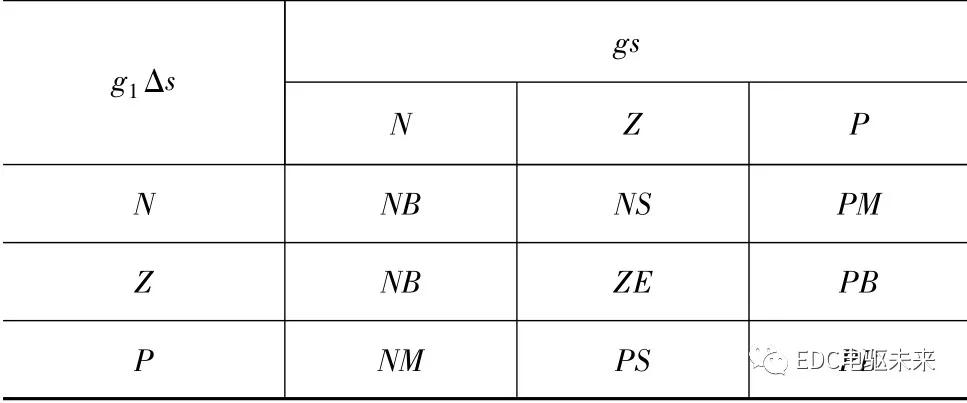
当Δd较大时，上述控制仍有可能诱发系统抖振。根据文献［26］，本文中采用模糊系统取代饱和函数；模糊系统呈现出边界层内具有非线性斜坡的饱和函数特性。取gs和g1Δs为模糊系统输入变量，输出为u fsmc，非线性控制律可表示为
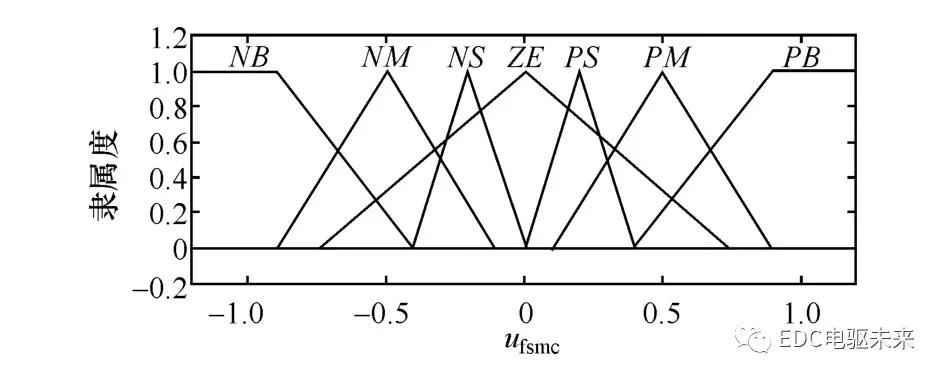
将模糊系统输入变量gs和g1Δs划分为负（N）、零（Z）和正（P）3类模糊集合，输出变量划分为负大（NB）、负中（NM）、负小（NS）、零（ZE）、正小（PS）、正中（PM）和正大（PB）7个模糊集合；以三角函数作模糊隶属度函数，见图6和图7；应用Mamdani模糊模型，系统模糊规则设计见表2；利用质心法进行输出变量解模糊化。
图6 输入变量gs和g1Δs隶属度函数
图7 输出变量u fsmc隶属度函数
表2 模糊规则
由于扰动估计误差Δd上界难以准确获取，k（t）无法精确得到。因此，设计自适应律如式（18）。
式中βk为自适应速率。
3.2.3 稳定性分析
定理1（见文献［27］）对于给定非线性不确定系统（式（8））及滑模面（式（12）），控制增益有上界，满足＜k（t）。
为分析系统稳定性，取Lyapunov函数V（t）如下：
｜s（t）｜＞φ时，联合式（13）和式（18），可得Lyapunov函数V（t）的1阶导数：
进一步，引入正实数（t）可等效如下：
根据定理1，可得
最终，得到Lyapunov函数的1阶导数（t）为
由式（25）可知，当ρ＜βkφ／（k a＋hφ）时，σ＞0，进一步地，（t）≤-k m V1／2-σ＜0，从而保证滑模变量s有限时间内收敛至零点。
4 仿真研究
为验证本文设计方法的有效性，针对电动汽车电制动系统制动模式切换及防抱死制动控制的动态过程开展了仿真研究，并与PI控制、MPC和ADRC等加载控制方法对比。仿真过程系统控制关键参数如下：ESO参数β1＝100，β2＝1000，α1＝α2＝0.75，δ＝0.2，AFSMC控制器参数c1＝0.05，βk＝8000；根据文献［28］对PI控制参数整定，取转速环带宽80 rad／s；ADRC和AFSMC＋ESO中ESO参数一致。
为量化评价加载控制方法的控制性能，采用转速跟踪均方根误差作评价指标，表达式为
式中：δRMSE为转速跟踪均方根误差；n为采样点数。
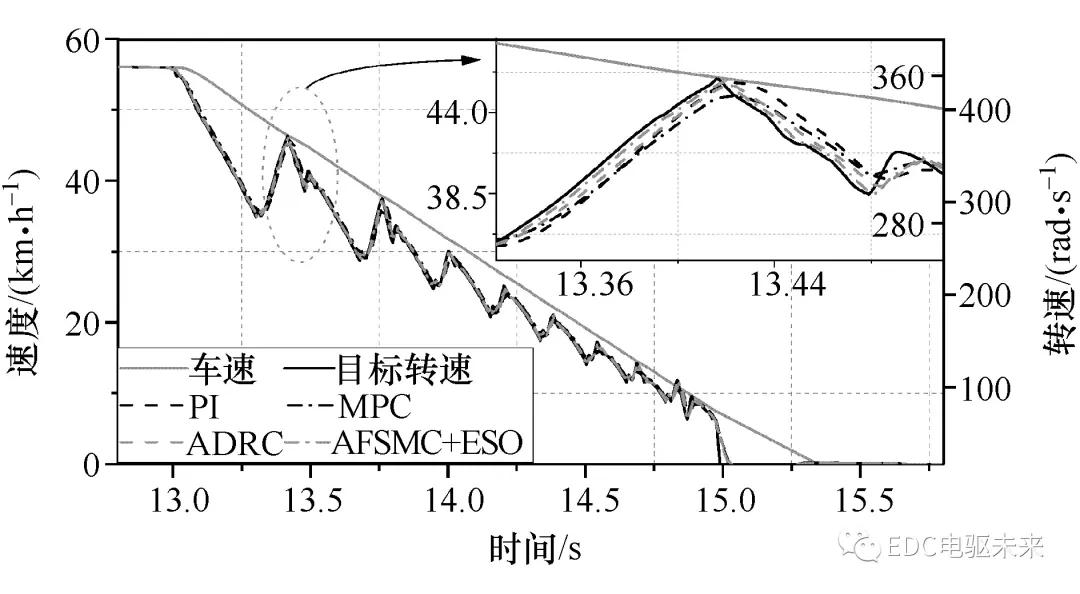
4.1 制动模式切换
正常行驶条件下，采用最大电机制动力矩策略对车辆制动。制动初速度50 km／h，踩制动踏板并保持主缸压力3 MPa；车辆减速至25 km／h时，电机失效撤出，电制动力矩减小至零，液压制动力矩增加，制动模式由纯电制动向摩擦制动过渡，如图8所示。
由图8（a）可知，受传动环节弹性及齿隙影响，制动模式切换瞬间发生传动系扭振，电制动系统转速（台架目标转速）高频振荡，振幅高达17.4 rad／s，振荡频率达6.4 Hz。传统PI及MPC控制下，台架实际转速较目标值有较大滞后，且跟踪精度低，最大转速跟踪误差幅值分别为13.54和8.51 rad／s；而ADRC和AFSMC＋ESO负载模拟动态性能较好，且具有较高的控制精度，最大转速跟踪误差幅值减小至6.19和3.17 rad／s；其中，AFSMC＋ESO具有最高的响应速度和控制精度，台架实际转速紧跟目标值，负载模拟性能更佳。
图8 制动模式切换过程负载模拟效果
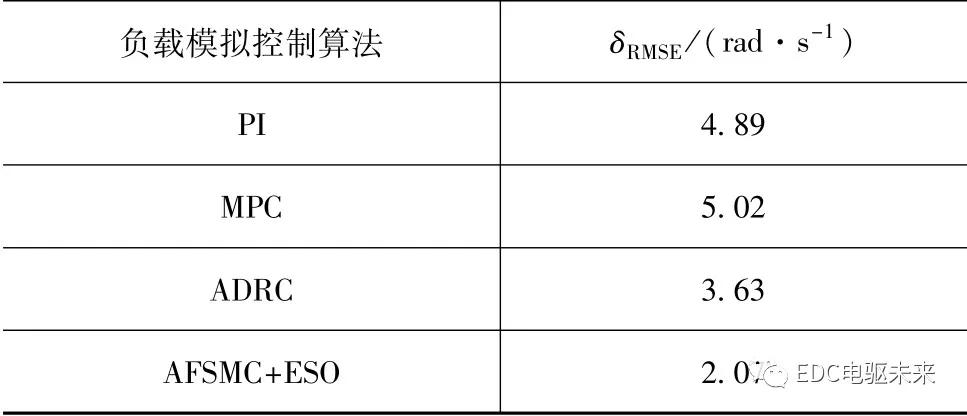
取15.75～16.6 s为制动模式切换过程起止时间；按式（26）计算负载模拟量化误差见表3，提出的AFSMC＋ESO量化误差最小，模拟误差较传统PI、MPC、ADRC分别减小77.8%、65.9%和46.6%。
表3 制动切换过程负载模拟量化误差
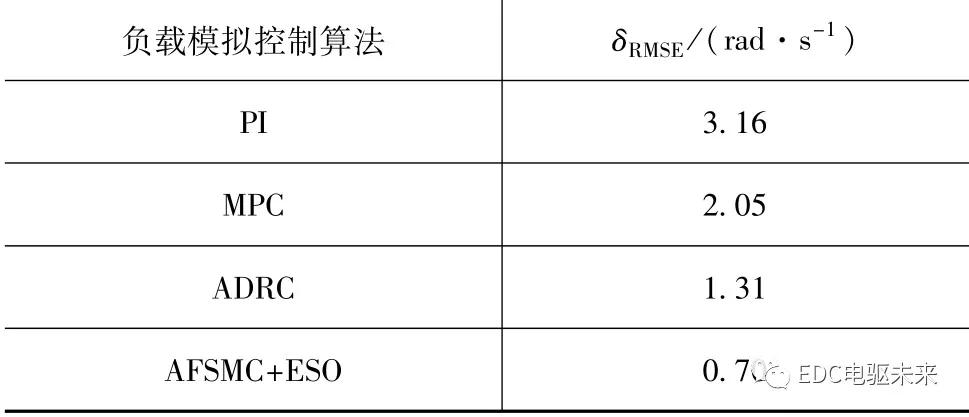
4.2 防抱死制动
高附路面，采用文献［26］中设计的防抱死控制作为测试对象。制动初速度50 km／h，踩制动踏板并保持主缸压力于12 MPa，触发防抱死控制。液压制动系统提供稳态制动力矩，电机动态调节出力使车轮滑移率稳定于期望值。图9为防抱死制动过程负载模拟仿真结果。
图9 防抱死制动过程负载模拟效果
由图9可知，传动环节非线性作用下，防抱死控制性能较差，电制动系统转速高频波动，波幅达77.8 rad／s，频率达5.2 Hz。传统PI和MPC控制下，台架实际转速较目标值有一定的滞后，负载模拟误差较大；而ADRC和AFSMC＋ESO负载模拟动态性能较好，台架实际转速紧跟参考值；其中，AFSMC＋ESO具有最高的响应速度和控制精度，负载模拟性能更佳。
取防抱死制动过程起止时间为13～14.8 s；按式（34）计算负载模拟量化误差，结果见表4，本文中提出的AFSMC＋ESO量化误差最小，模拟误差较传统PI、MPC、ADRC分别减小57.5%、58.8%和43.0%。
表4 防抱死控制过程负载模拟量化误差
5 结论
通过以上的分析和仿真研究，可以得到如下结论：
（1）建立了融合感应电机模型的车辆及台架机电一体化模型，该模型能够精确反映整车动力学控制台架测试时车辆、电机和测功机的机电特性，可适用于车辆动力学和测功机加载控制算法的开发；
（2）传动系弹性及齿隙特性，动态过程易引起传递力矩波动，进而诱发电制动系统运动状态高频振荡；为模拟此类高动态非线性负载，负载模拟算法应具备更高的动态性、抗扰性和控制精度；
（3）结合完全电模拟的负载模拟拓扑及速度跟踪控制的负载模拟方式，提出了自适应模糊滑模自抗扰的测功机加载控制算法，并与传统PI控制、MPC和ADRC对比；在SIMUlink中开展了制动模式切换及防抱死制动控制台架测试的仿真研究。结果表明：提出的负载模拟算法相对传统PI控制、MPC和ADRC，具有更高的控制精度及更高的响应速度；制动模式切换过程负载模拟量化误差较以上控制方法分别降低77.8%、65.9%和46.6%，防抱死制动过程负载模拟量化误差分别降低57.7%、58.8%和43.0%，负载模拟误差大幅减小。因此，该方法可确保台架测试数据真实可靠，为电动汽车制动控制策略台架测试提供理论指导。
广告 
广告
编辑推荐
最新资讯
-
荷兰Zepp氢燃料电池卡车-Europa
2024-12-22 10:13
-
NCACFE -车队油耗经济性报告（2024版）
2024-12-22 10:11
-
R54法规对商用车轮胎的要求（上）
2024-12-22 10:10
-
蔚来ET9数字架构解析
2024-12-22 09:53
-
4G/5G网络新时代的高效紧急呼叫系统NG-eCal
2024-12-20 22:33
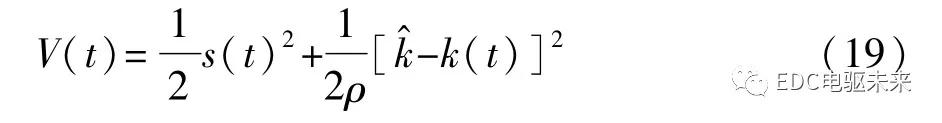
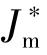
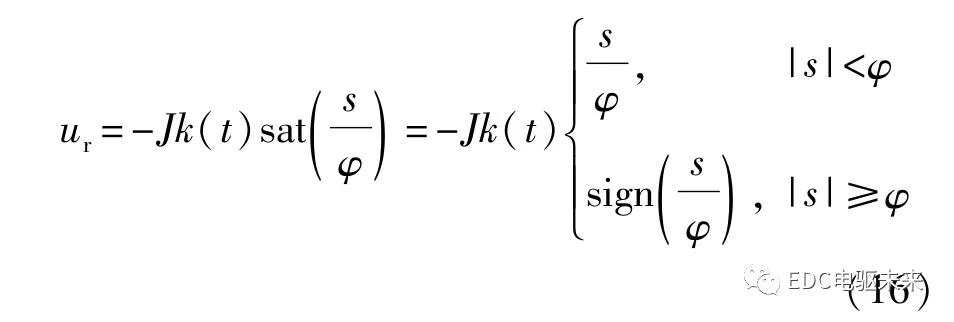
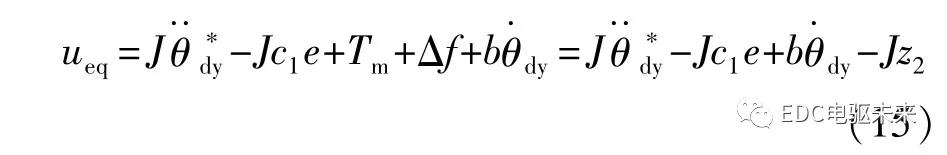
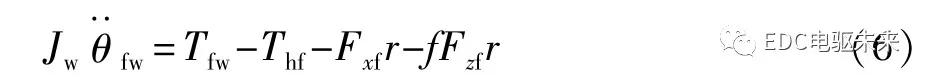
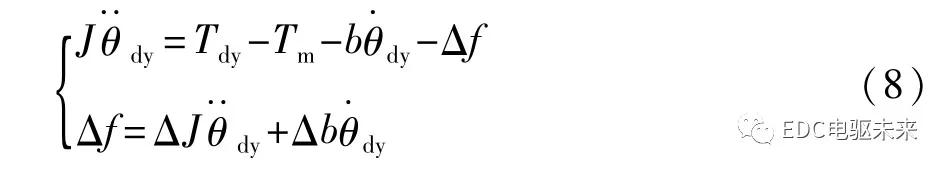
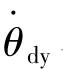
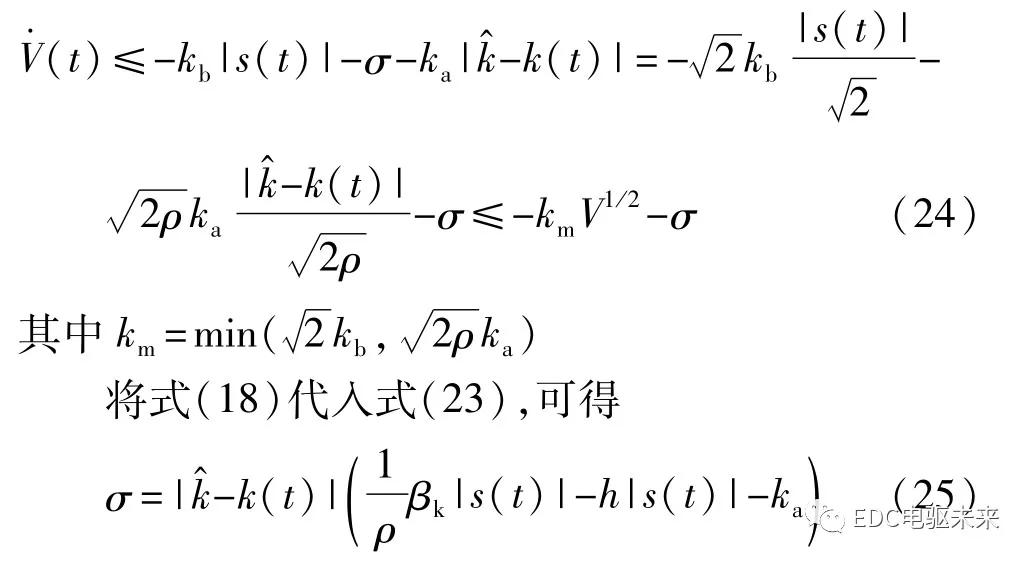
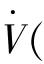
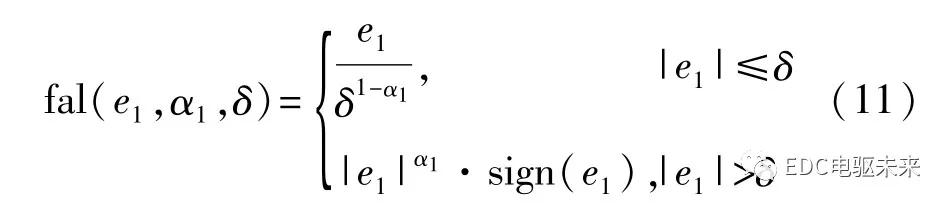
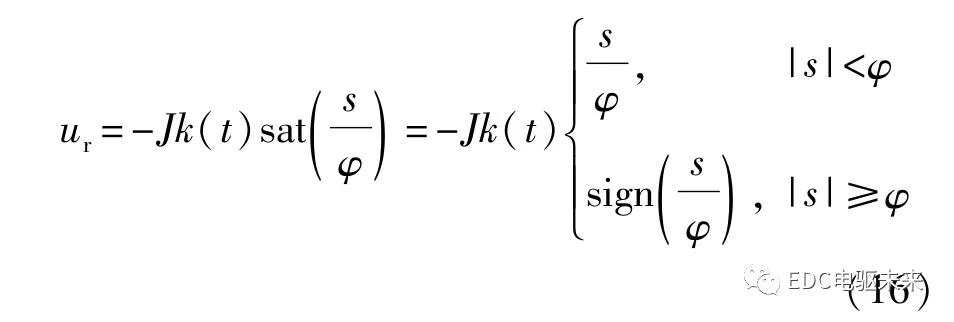
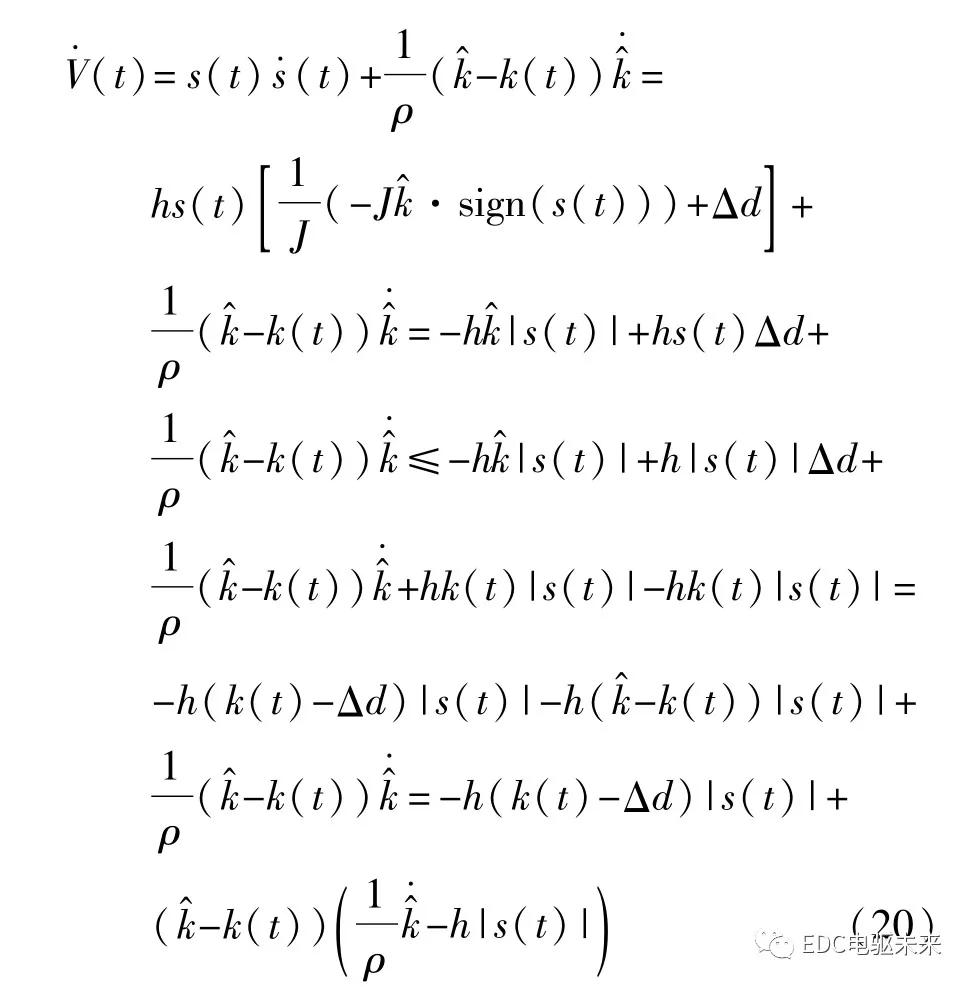
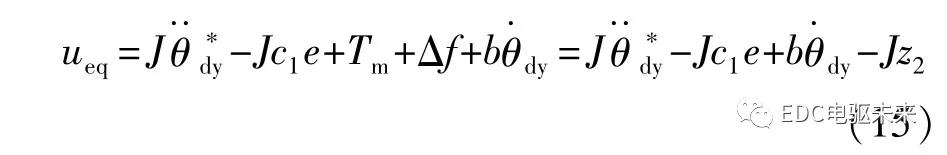
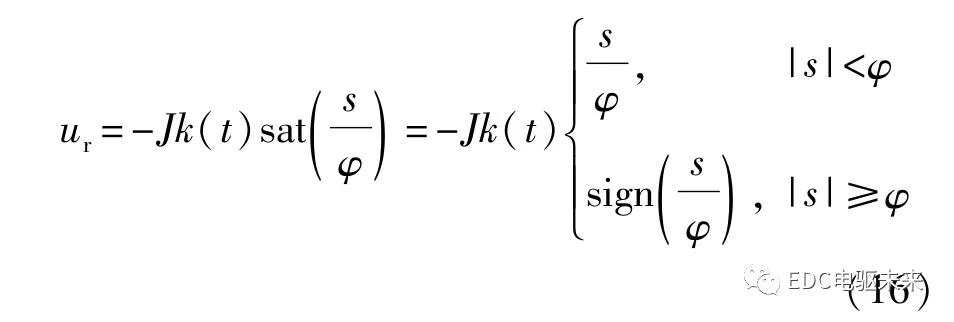
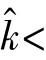
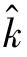
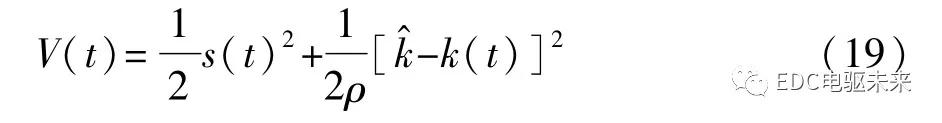
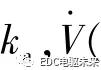
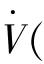
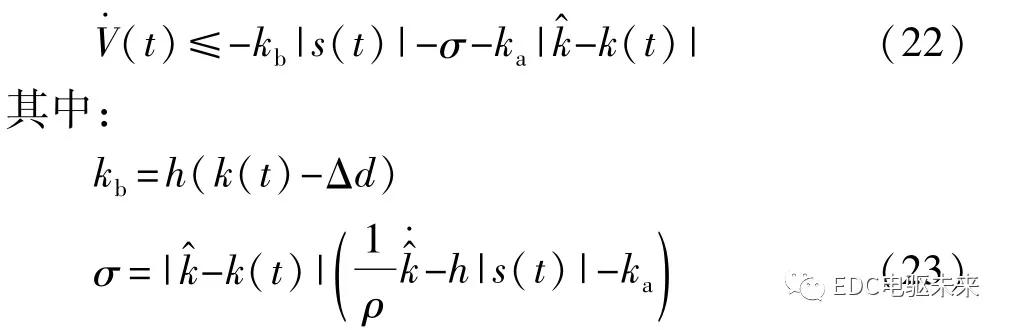
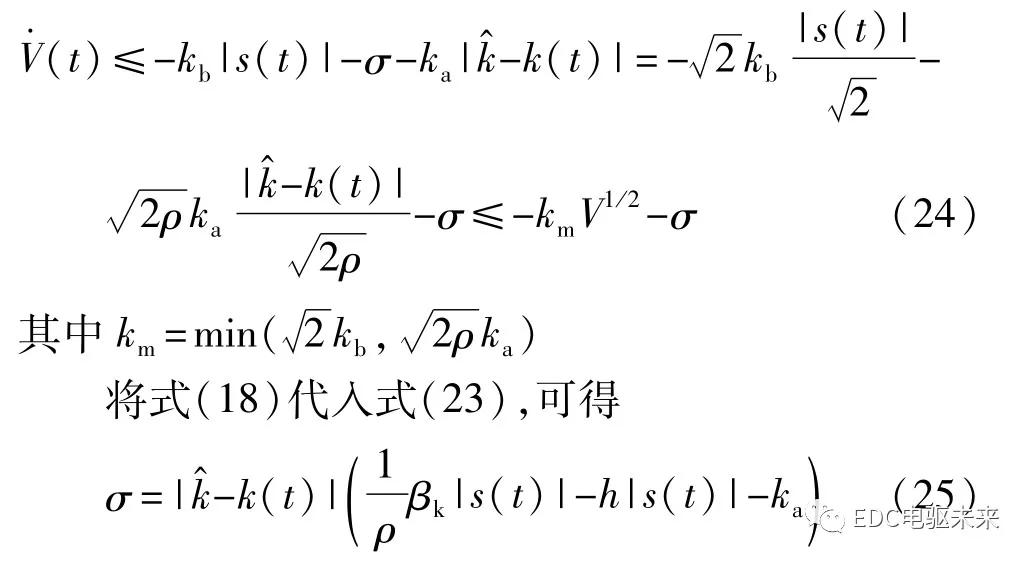
广告
广告
