广告
用直接模拟和混合方法模拟空调风道噪声
2020-05-13 23:37:27· 来源：STAR CCM Online
现代汽车设计对乘员舱舒适性要求越来越高，空调噪声是影响汽车舒适性的主要因素之一。空调噪声一方面来源于风机运行时在腔体内产生的噪声，另一方面是气流在风道
现代汽车设计对乘员舱舒适性要求越来越高，空调噪声是影响汽车舒适性的主要因素之一。空调噪声一方面来源于风机运行时在腔体内产生的噪声，另一方面是气流在风道传播过程中引起的噪声。风道对流动及噪声的产生与传播有重要影响。本文将以一个简化的HVAC风道为基础，说明两种常用的管道噪声模拟方法，模拟结果将与参考文献1中的实验数据进行对比。
几何：简化的风道
为了与实验数据进行对比，仿真分析所用的几何与实验风道保持一致，如图1所示，为一段矩形截面弯管，其中内置一块倾斜的阻力板。入口段长3m，90°弯头内径为4cm，阻力板位于弯头和出口之间，倾斜角度30°，风道内截面尺度为8cm×8cm，壁厚1cm。
图1 简化的风道几何
实验中为了获取远场声学数据，以风道出口为中心，安装了半径为1米的半圆形装置，上面共布置了289个传声器，所有传声器都与风道出口相距1米。为了对比数据，仿真计算中设置相同数量和位置的测点，如图2所示。
图2 几何和远场测点位置
实验中的平均流速为7.5m/s，气流通过弯头时发生分离并形成回流区。由于分离产生的非稳态剪切层撞击到阻力板，从而在阻力板壁面上产生非稳态压力载荷。绕过阻力板后形成湍流旋涡，然后排放到风道外的静止区域。流场结构如图3所示，流动不稳定性清晰可见。
图3 以非稳态密度梯度显示的流场结构
数值方法
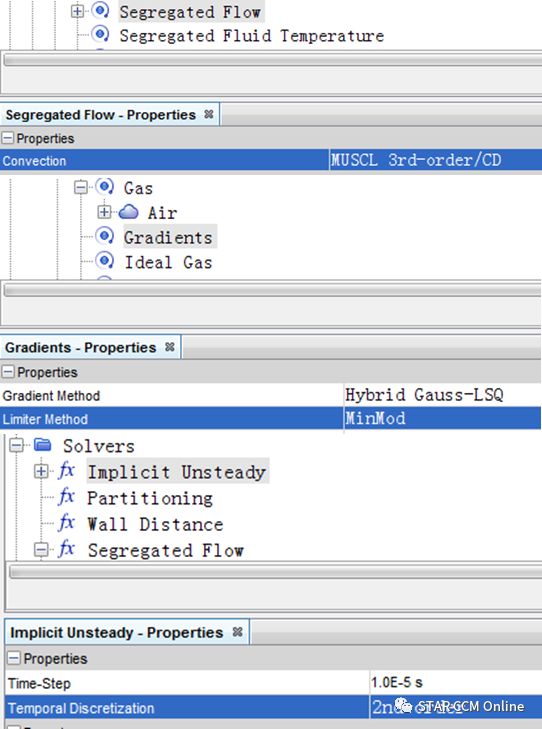
两种仿真方法均用Star-ccm+完成，对流格式采用MUSCL 3rd-order/CD，通量和梯度计算采用混合高斯最小二乘法（Hybrid Gauss-LSQ）结合MinMod梯度限制器。算法为SIMPLE，时间步用二阶精度、向后差分格式，如图4所示。湍流模拟用LES结合WALE次网格尺度模型。
图4 主要求解设置
直接模拟
方法概述
直接模拟方法中，声音的产生、传播以及流体的流动都是通过求解非稳态可压缩NS方程求解的。这种方法对数值求解精度要求很高，求解所用的网格要非常精细，并且需要无反射边界条件，所以计算成本非常高。用直接模拟方法计算远场噪声，需要超大规模的并行才能实现，但对于近场噪声，直接模拟方法是可行的。对于风道的噪声研究，可以考虑用直接模拟方法。
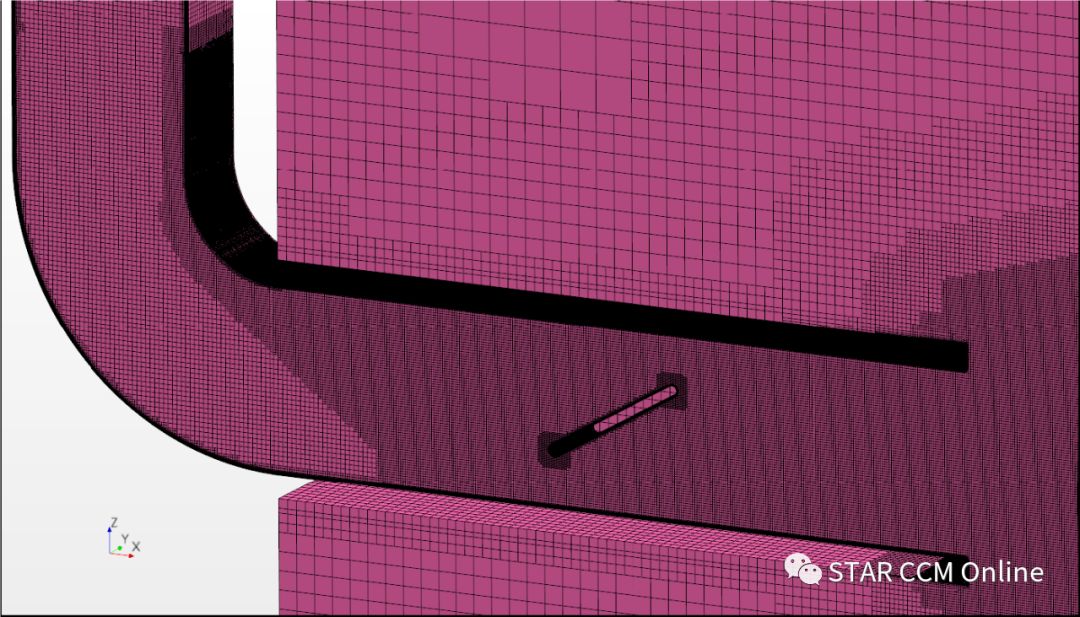
本文所用的网格为带边界层的Trimmer网格，弯头和阻力板附近网格尺寸为1mm，风道出口与测点之间的区域逐渐增长为约1.6cm，测点到计算域出口之间的区域网格进一步粗化。图5表示了网格总体分布形式，图6是关键区域放大图，其中边界层网格y+<1，增长比1.2，x+和z+≈18.
图5 直接模拟计算域中截面网格
图6 弯头和阻力板附近网格放大图
在参考文献1的实验中，在长3m的进气管段安装了一个锥形喷嘴，具有部分反射特性，从而在产生的压力谱中出现共振峰。而模拟中仅包括0.5 m的进气管段，并且进气管是无反射的。因此，预计不会捕捉到共振峰。
无反射处理
为了尽可能地防止边界的反射波进入计算域，Star-ccm+提供了三种策略：Free Stream边界、声学抑制区模型（Acoustic Suppression Zone model）、网格拉伸（Grid Stretching）。三种方法可以同时使用，从而获得最优的求解效果。
1) Free Stream是一种边界类型，对抑制法向撞击到边界的声波非常有效，但是对入射的斜波仍会有部分反射，对对流涡的扰动敏感。设置时只需要把指定边界的类型选为Free Stream，指定相应的参数即可。
2) 声学抑制区模型（Acoustic Suppression Zone model）通过在流动控制方程的右侧添加适当的阻尼项来抑制可能会到达边界的流动扰动，从而在边界位置产生准非反射响应，即允许扰动穿过边界而不会反射回计算域。
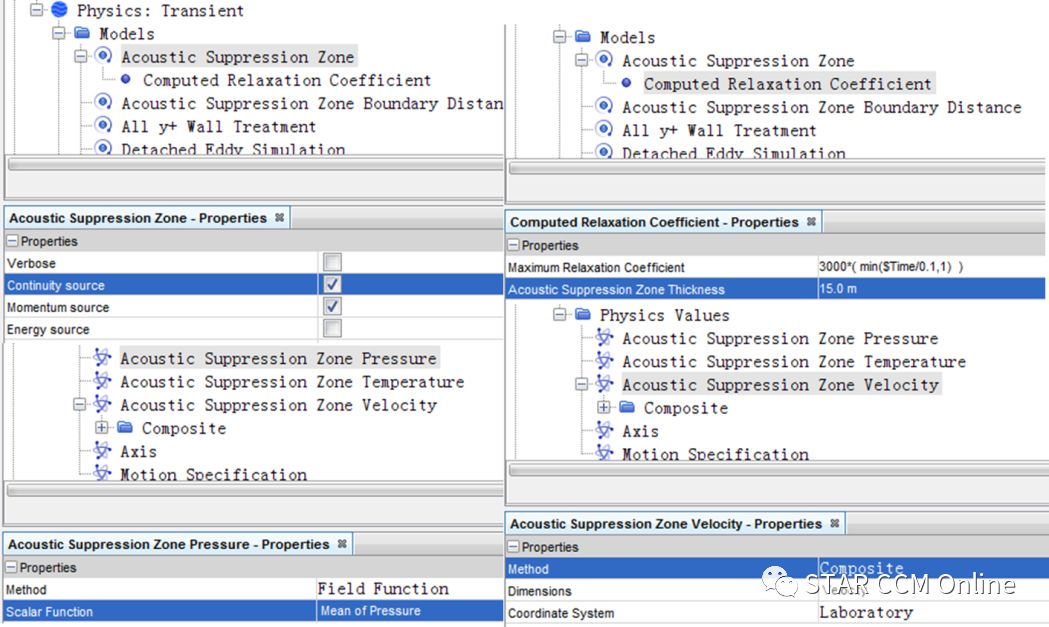
设置声学抑制区模型需要首先在Models中激活Acoustic Suppression Zone，设置相应的模型参数，并在Regions > Fluid >Physics Values中设置压力、温度、速度等变量的目标值，界面如图7所示。
图7 声学抑制区模型主要设置
3) 网格拉伸（Grid Stretching）的概念很简单，就是在远场区域生成尺寸逐渐增长的拉伸网格，直到声波被数值耗散分解和衰减。这种方法不需要调整求解参数，也没有要记录的主流状态，但是过度拉伸也会引起反射。在拉伸区域会导致网格量增加，但与声学计算的网格总量相比，通常可以忽略不计。
最有效的方法是以上三种策略同时使用，外边界使用Free Stream类型，边界的上游添加声学抑制区，并划分拉伸网格，本文中就同时应用了三种策略，最大程度地抑制声波反射：
1) 出口边界类型为Free Stream；
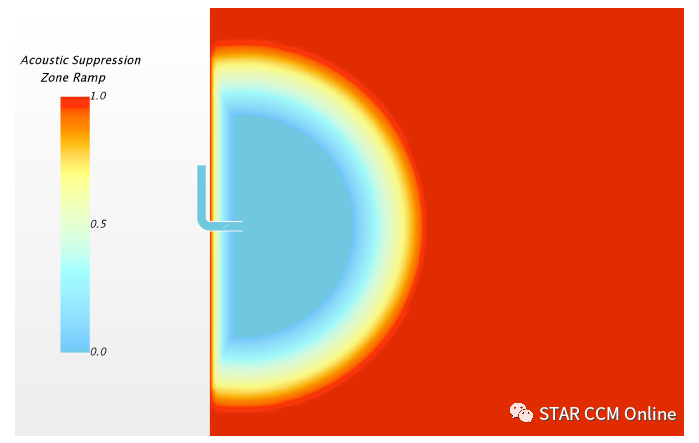
2) 激活声学抑制区模型，海绵区的斜坡函数从测点位置附近开始，是风道出口到半圆面的径向距离的二次函数，以实现对入射声波的最大吸收。斜坡函数的形状如图8所示。
图8 声学抑制区海绵层斜坡函数(Ramp Function)
3) 出口侧的网格逐渐粗化，使湍流到达出口之前被耗散。
为了得到准确的流动边界，首先完成一段入口管的稳态RANS计算，进出口都采用周期边界，得到充分发展的流动变量边界值，提取这些边界值后用于整段风道的稳态RANS计算的入口边界值，然后再将整段风道的稳态RANS结果作为LES的初场，以缩短LES的启动时间。
数据采样方法
可压缩直接噪声计算存在一个问题，就是压力场中既包含流体压力，又存在声学压力，且难以区分两者的贡献值。当前的设置中，风道内的湍流会撞击到一些测点，所以声学结果中会包含流体动力的成分，并不能保证完全是声学数据。
由于湍流压力波动大于声压波动，如果不做处理，湍流压力将占主导地位。有两种采样方法可以从结果中移除流体动力的成分。
在第一种方法中，从模拟的早期阶段提取一小段时间的数据。选择的时间段应满足以下要求：在开始取样之前，风道弯头处和阻力板周围的流动已经发展，在发展的湍流到达测点之前停止取样，以减少测点数据受湍流压力的影响。采样总时间为0.04s，分成3个重叠率为50%的块，频率分辨率为50hz。由于时间信号较短，无法评估气流是否充分发展。因此，这种处理方法的结果仍然会受到流场不确定性的影响，但另一方面，测点处的流体压力波动对结果的影响会大幅减小。
第二种方法中，为了获得采样时间较长、流场不确定性较小的信号，计算至阻力板周围区域的速度均值和方差达到统计收敛，之后，记录0.3s的声学结果。使用11个0.05s的块，50%重叠，获得频率分辨率为20hz的频谱。为了减小流体动力的影响，在风道外的湍流区引入了一个人工增粘区。人工粘性从风道出口处0.1米开始，为了不干扰声源区域，所用的大小应尽可能地阻尼湍流结构，同时足够低，不至于耗散传播的声波。由于声波传播对粘度的敏感度相对较低，所以这样处理不会导致测点处的声压级衰减。
结果分析
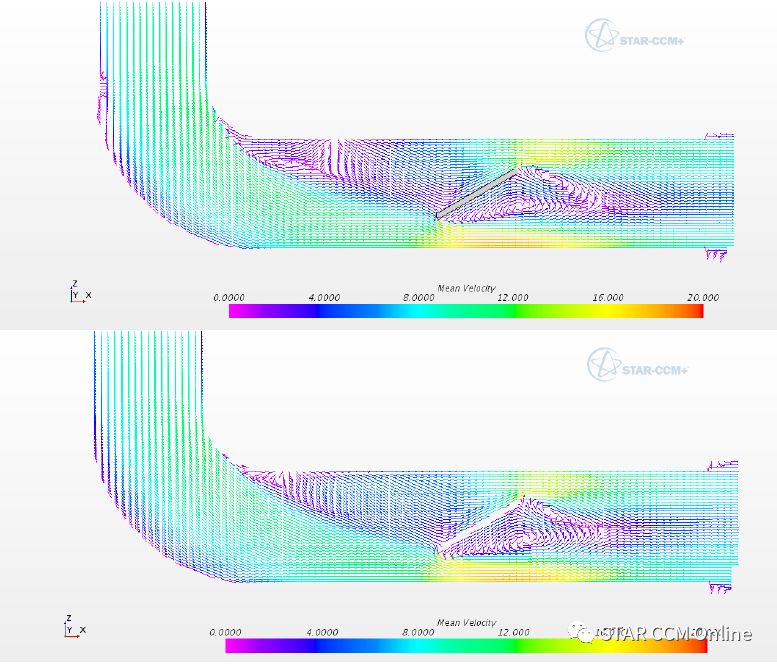
图9上图显示了直接模拟得到的风道中截面流场，可以看出，与图3所示的实验结果是定性一致的。
图9 时均流场矢量图，上图可压缩，下图不可压缩，分离点的偏差是由于两种方法所用的壁面分辨率不同造成的。
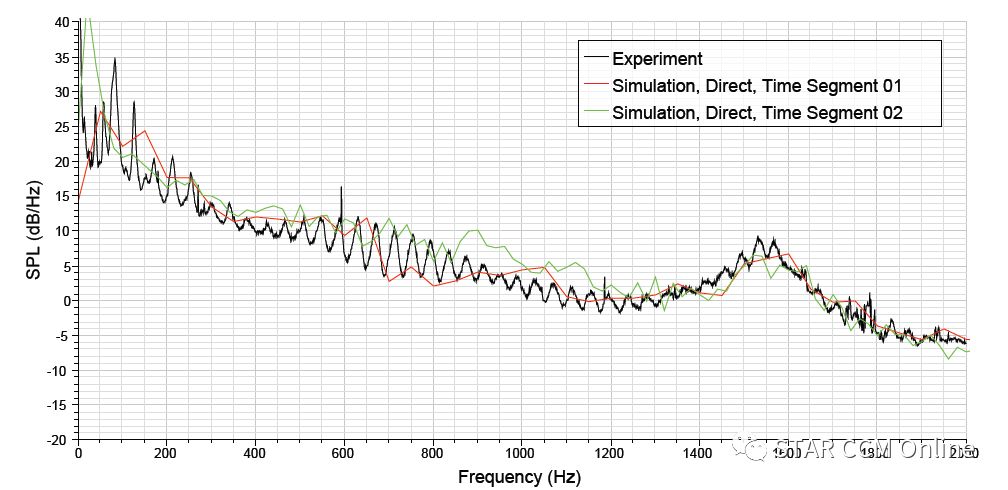
非稳态可压缩模拟的压力波由图2所示的各个测点记录。对单个测点的频谱进行平均，得到如图10所示的频谱图。模拟开始时所取的较短时间间隔的结果标记为“TimeSegment 01”，而较长时间信号的结果标记为“TimeSegment 02”。由图可见，模拟结果合理地捕捉到了实验的趋势。两个结果都与流场不确定性有关，这是由于湍流对测点处的冲击会带来流场压力波动的影响。
图10 可压缩直接噪声模拟结果与实验值对比
混合模拟方法
方法概述
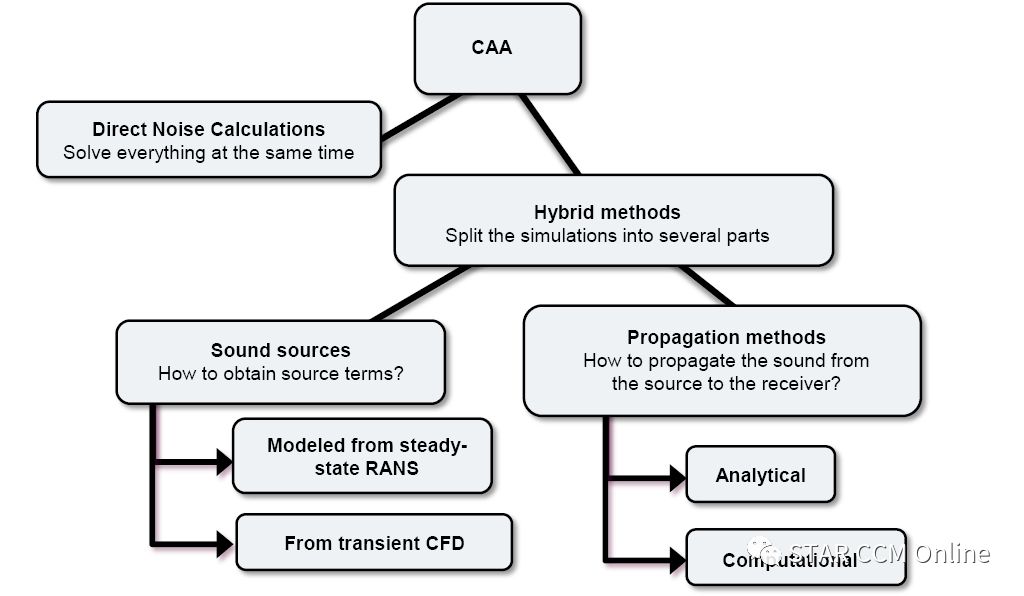
第二种模拟方法是基于不可压缩CFD的混合方法。Star-ccm+提供的声学模拟方法概览如图11所示。混合方法的一个重要优势是可以把流体压力和声压波动分开求解，对近场流动用非稳态的雷诺平均、DES或LES等方法求解，然后再把求解结果作为噪声源，通过求解声波方程得到声学数据，所以可以直接处理声学结果，避免了在可压缩直接模拟方法中存在的困难，即测点处由于受到湍流冲击而产生流动压力波动，从而影响声压结果。
混合方法中计算声源的模型有：
Ffowcs Williams-Hawkings Model，
Lighthill Stress Tensor Model，
Curle Noise Source Model，
Goldstein Axisymmetric Noise Source
Model ，
Proudman Noise Source Model等。
声传播可以用解析法或计算法求解，解析法通过各种公式对声源求积分得到接收点处的声音信号，计算法则求解声扰动的偏微分方程。
图11 Star-ccm+噪声模拟方法概览
混合方法中，声波方程与CFD模拟在同一网格上同时运行，因此不需要在流场与声场之间存储或映射数据。基本的CFD仍然用Trimmer网格计算，网格尺寸与可压缩模拟大致相同，但壁面分辨率稍低，数值格式和设置也是类似的。
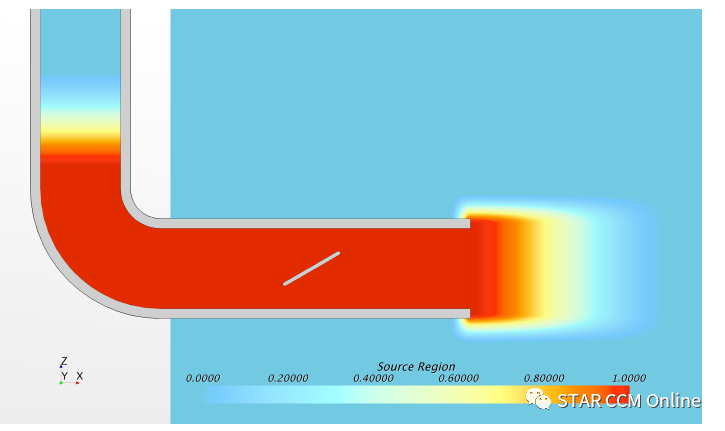
使用混合方法的一个优点是，可以定义一个声源区域，其中的声源项可以由不可压缩流动求解进行评估，并用于声波方程。本例中的源项如图12所示，只有在已定义的声源区内的声源会影响到声辐射，声源区外的结果不会影响测点处的声信号。声源区的调和值(Blending Value)为1.0表示充满声源，而值为0表示没有声源。源项调和值平顺渐变，避免源项突然截断而产生的虚假声源。此外，在声波方程中加入一个阻尼项来衰减传向开放边界的声波。阻尼项的斜坡函数与直接模拟所用的斜坡函数形状相似，如图7所示。
图12 混合方法的声源区域
结果分析
主流场如图8下图所示，与参考文献1的PIV测量结果定性一致。与直接模拟的结果相比有所不同，这是由于弯头处使用的壁面分辨率稍有不同，导致分离点存在差异。
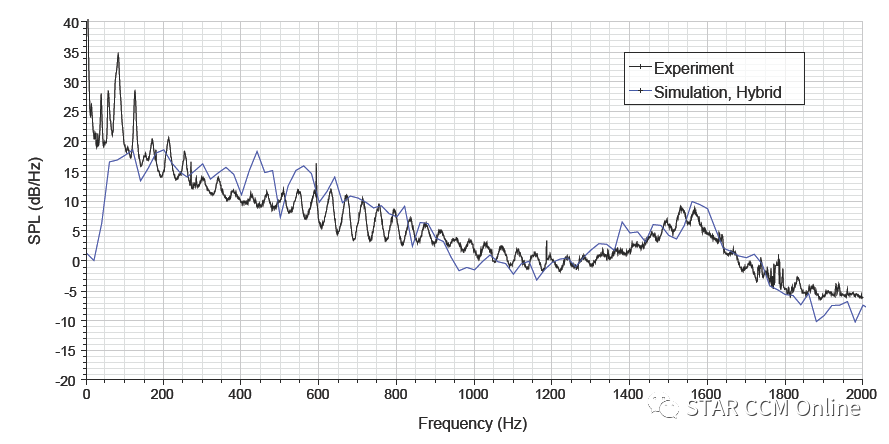
与可压缩直接法一样，混合模拟中的声场记录在远场的测点上。图13对模拟结果与实验数据进行了对比，可以看出，混合模拟的结果与直接法和实验相比，均具有定量可比性。
图13 混合方法模拟结果与实验值对比
总结
本文用两种方法模拟了简化的HVAC风道噪声。第一种方法采用直接计算方法，通过求解非稳态可压缩Navier-Stokes方程，同时模拟流场和噪声；第二种方法是混合方法，分别求解不可压缩CFD和声波方程。结果表明，两种方法可以得到类似的结果，都可以捕捉实验数据的变化趋势。由于模型中没有包含扩展的入流风道，所以无法捕捉到与此相关的风道共振现象。在实验装置中，有些测点位于由风道出口引发的湍流中，而湍流引起的流体压力波动会污染直接计算方法的声学结果。在测点周围的湍流区引入一个特殊的人工粘性区域来减小这种影响，从而获得准确的声学结果。混合方法中不需要处理湍流压力波动，因为流场和声场是分开求解的，这是混合方法的明显优势。
参考文献：
1) A. Jäger et al.,Numerical and Experimental Investigations of the Noise Generated by a Flap in a Simplified HVAC Duct, AIAA 2008-2902, 29th AIAA Aeroacoustics Conference, 2008.
2) Axel Kierkegaard et al., Noise Simulations using Directand Hybrid ethods, AIAA 2016-2855
3) STAR-CCM+ User Guide
广告
广告
编辑推荐
最新资讯
-
谱尼集团河南总部大厦落成并正式入驻运营
2024-11-26 21:30
-
谱尼测试集团山东区域总部大厦落成仪式圆满
2024-11-26 21:26
-
一图读懂丨谱尼测试2024年半年度报告
2024-11-26 21:25
-
谱尼测试获评“2024年苏州市服务业数字化转
2024-11-26 21:24
-
谱尼测试上海电磁兼容实验室扩能投运
2024-11-26 21:23
广告
广告
