广告
斜齿圆柱齿轮载荷分布及热弹流温度场分析
2020-07-06 12:06:46· 来源：EDC电驱未来
作者：薛建华，张振华丨陕西汉德车桥有限公司摘 要啮合面载荷分布是斜齿轮设计和强度校核的基础。以传动误差为基础，基于啮合面和端面刚度建立了斜齿轮单位线载
作者：薛建华，张振华丨陕西汉德车桥有限公司
摘 要
啮合面载荷分布是斜齿轮设计和强度校核的基础。以传动误差为基础，基于啮合面和端面刚度建立了斜齿轮单位线载荷分析模型，通过数值解法得到了斜齿轮啮合面上单位线载荷和转角误差分布。为便于设计和校核，建立了既综合考虑齿廓因素和轴向因素，又能反映啮合面载荷的特征坐标系。将斜齿轮副简化为两个反向圆锥台接触模型，完善了斜齿轮热弹流分析模型，得到了斜齿轮接触点油膜压力、厚度和温度场分布，得到了沿特征坐标分布的闪温。结果：斜齿轮齿廓中部承担了大部分载荷，其变化规律与转角误差相同。
1.引言
平行轴斜齿圆柱齿轮是高速重载传动中的首选，其重合度高，传动平稳，振动和噪音小，已得到广泛应用。斜齿轮啮合过程中单位线载荷的计算是斜齿轮设计和强度校核的基础。 热弹流分析是校核承载能力的重要方法。
本文将载荷和热弹流计算引入工程应用，通过转角误差基于啮合面和端面刚度得到了斜齿轮啮合面上每一点的单位线载荷分布，提出了简化斜齿轮设计和强度校核的特征坐标系，建立了考虑润滑油粘合和密度随温度和压力变化的斜齿轮热弹流分析模型，得到了啮合面上的热弹流温度场，为斜齿轮设计与校核奠定了理论基础。
2.斜齿轮单位线载荷计算
2.1.斜齿轮单位线载荷分析模型
斜齿轮在传动过程中由于受载变形会产生传动误差，如式(1)所示，式中Δθ为传动误差角，rb2为从动轮基圆半径。则该点单位线载荷为w=kδ。设该时刻接触线总长度为L，不考虑基节误差，则必满足载荷平衡方程，如式(2)，P为输入功率n1为小轮转速，rb1为小轮基圆半径。
2.2.斜齿轮单位线载荷计算
斜齿轮端面刚度可以由石川模型求得，斜齿轮参数如表1所示，斜齿轮端面刚度分布如图1所示。
Table 1.The parameters of the helical gear
表1.斜齿轮参数
Figure 1.The stiffness distribution of helical gear end face
图1.斜齿轮端面刚度分布
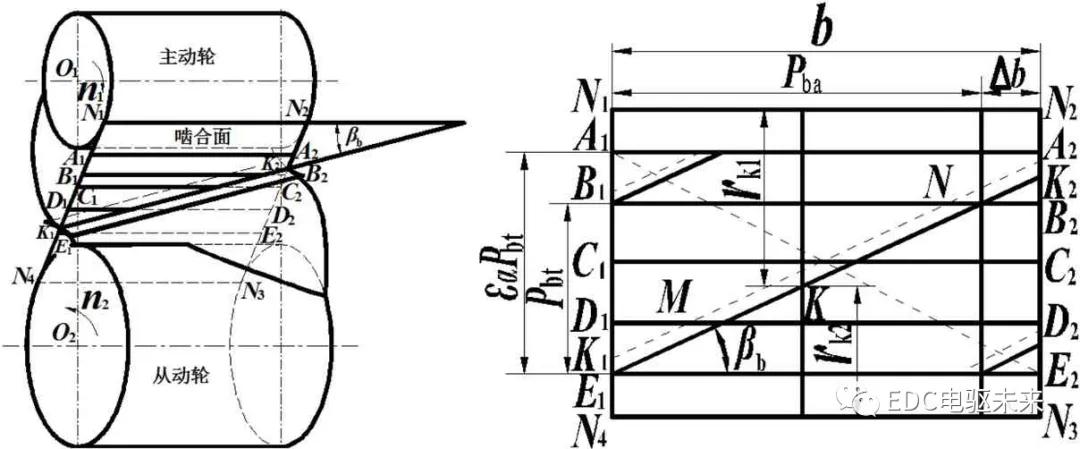
斜齿轮啮合面N1N2N3N4为其基圆内公切面，如图2所示，接触线K1K2为与轴线成基圆螺旋角βb的线段，根据端面啮合状态，可以将啮合区分为双齿啮合区A1A2B1B2、D1D2E1E2和单齿啮合区B1B2D1D2，在双齿啮合区内，接触线总是对应成对出现的。设齿轮副从A1点啮入，E2点啮出，斜齿轮轴向重合度，设εβ=n+Δεβ，n为整数。nPba对应的区域内，接触线总长度为常数，由式(3)计算，其总载荷为，将端面实际接触长度A1E1离散化，设N为划分节点数，则nPba对应载荷如式(4)。
Figure 2.The meshing model and contact face of helical gear
图2.斜齿轮啮合模型及啮合面
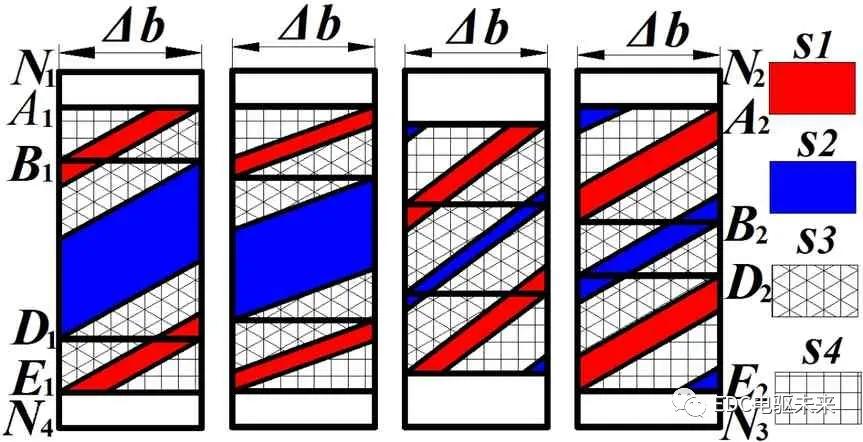
Δb=ΔεβPba对应的接触线长度和分布规律是随时间变化的，与ΔB和βb大小有关，可分四种情况，如图3所示，在s1 区域，接触线长度最长，s2 区域最短，其余区域是渐变的，啮合线长度LΔ为该时刻各段接触线长度之和，WΔ为各点单位线载荷之和，设某时刻共有m条线段参与啮合，每条线段上离散后点数为num，则有：
Figure 3.The analysis model of length of the contact line of helical gear
图3.斜齿轮单位线载荷分析模型
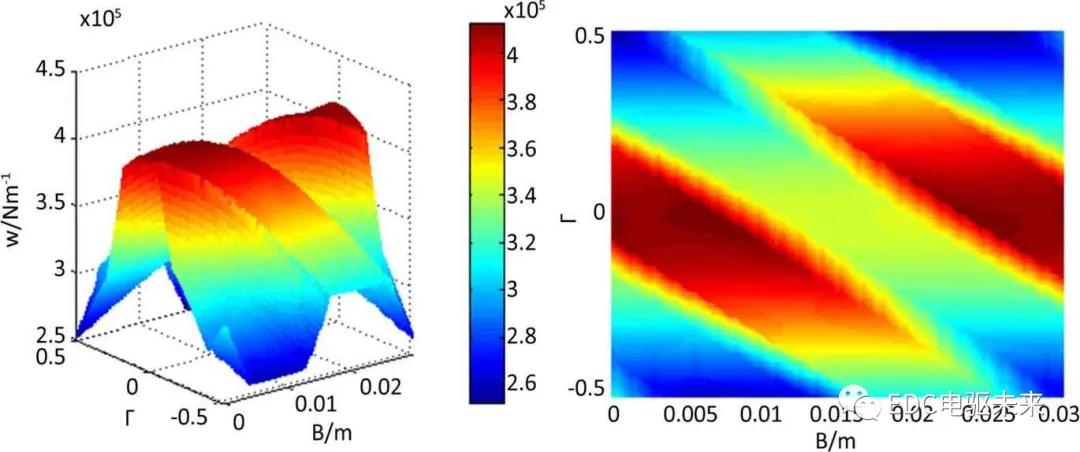
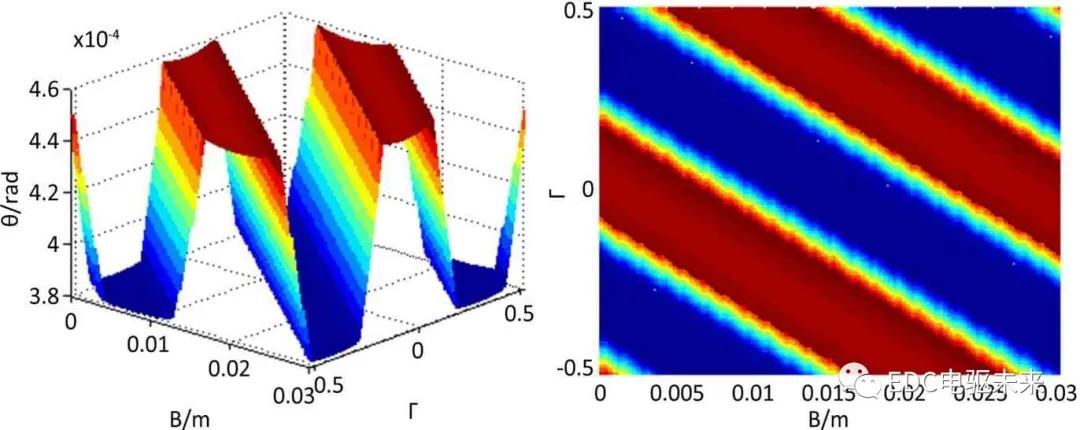
斜齿轮接触线总长度如式(6)，总载荷如式(7)。采用数值计算方法，取初值L=Ln和k0，求得 Δθ0，由式(7)得到总载荷W0，根据总载荷与实际载荷差值修正Δθ，直到载荷精度满足要求，即得到该时刻的转角误差Δθ，根据w=kδ得到接触线上该点的单位线载荷。其啮合面单位线载荷如图4所示，啮合过程中转角误差分布如图5所示，斜齿轮单位线载荷分布趋势与转角误差规律相同，呈方波状分布，方向与齿宽方向成βb角度，只是由于各点啮合刚度不同，齿廓中部单位线载荷比较大，齿顶和齿根单位线载荷较小。
Figure 4.The unite-linear load distribution of helical gear
图4.斜齿轮三维单位线载荷分布
Figure 5.The 3D transmission error distribution of helical gear
图5.斜齿轮三维传动误差分布
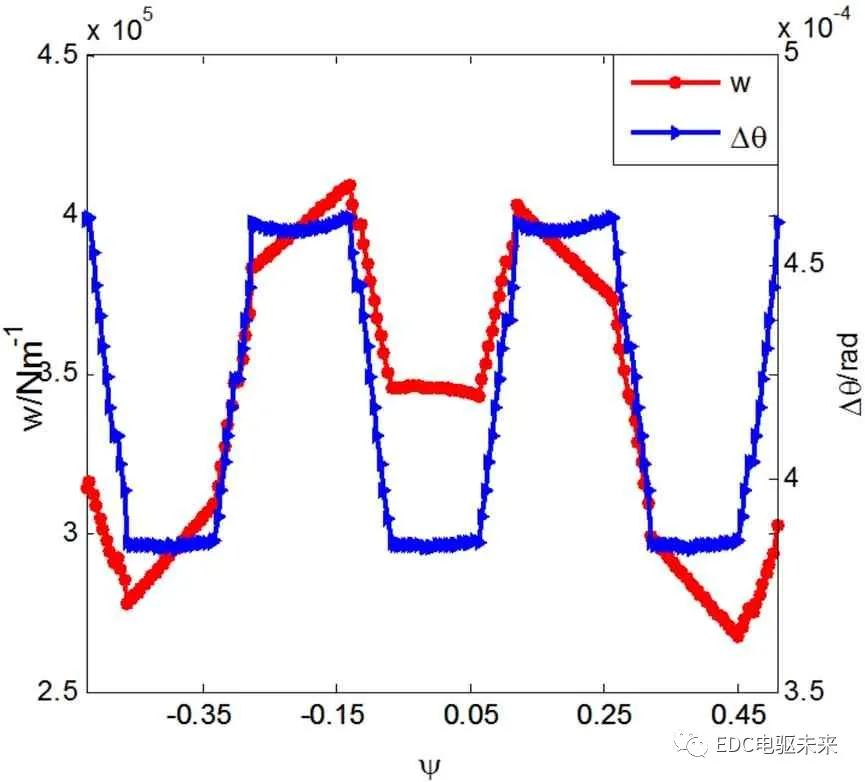
斜齿轮啮合面上每一点单位线载荷、滑动速度、曲率半径等不同，其载荷分布、应力分布、温度分布均应为三维模型，但三维模型计算量大，设计或校核运算周期长，而实际设计和强度校核过程中，往往只关心危险点的强度，故为了既能承载斜齿轮相关信息，又能体现斜齿轮本质，建立斜齿轮特征坐标系，用线段上各点来表征整个啮合面信息，坐标采用各点齿廓坐标，为示与端面坐标区别，用无量纲坐标Ψ 表示，定义与Γ 相同，特征坐标经过啮入点和啮出点，啮入点和啮出点接触线长度最短，滑动速度大，曲率半径小，故为斜齿轮最危险点之一，线段既包含了齿廓方向信息，也包括了齿宽方向信息。特征坐标下单位线载荷和转角误差如图6所示，显然，啮入点载荷和对应轴向最大值基本相同，转角误差也相同，因此特征坐标能反映整个啮合面的变化情况。
Figure 6.Unite-linear load and transmission error distribution of helical gear
图6.斜齿轮单位线载荷和传动误差分布
3.斜齿轮热弹流计算
3.1.斜齿轮分析基本模型
齿轮系统在运转过程中会在接触处形成润滑油膜，由于挤压和粘性剪切，油膜内能增加，温度升高，通过对流换热和热传导使齿轮温度升高。热稳态时，轮齿本体温度高于润滑油温度，因此在进入啮合瞬间，轮齿作为热源对润滑油加热，使润滑油温度升高，由于油膜极薄，几乎接触瞬时润滑油温度即与本体温度一样，以往研究均以热稳态润滑油温度为入口油温，这在接触区前半段，润滑油界面温度低于轮齿温度，这与实际不符，本文以热平衡时本体温度作为初始温度t0，使热弹流温度更符合工程实际。
3.1.1.斜齿轮热弹流基本方程
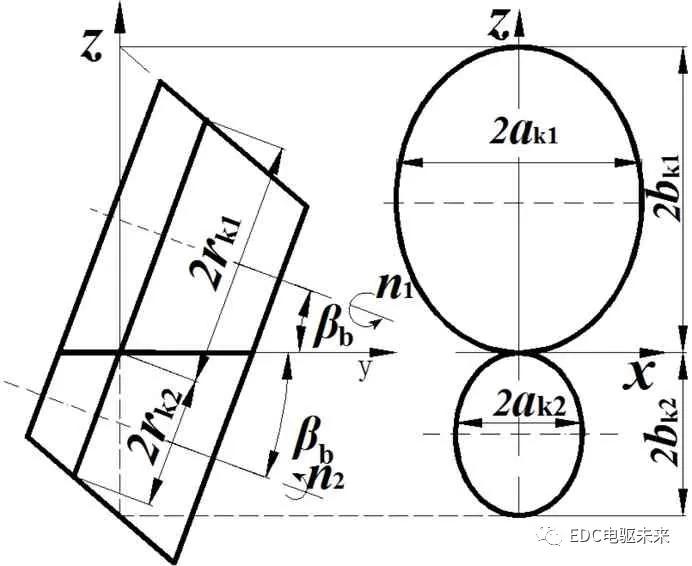
斜齿轮接触线上曲率半径沿齿宽是逐渐变化的，接触线上K点到N1N2距离即为主动轮曲率半径rK1，到N3N4距离为从动轮曲率半径rK2，可简化为两个个反向圆锥台相对滚动，如图7所示，在xoz平面内为两个椭圆，其长短轴如式(8)，在接触处曲率半径如式(9)。
3.1.2.热弹流基本方程
流体润滑雷诺方程为：
Figure 7.Contact analysis model of helical gear
图7.斜齿轮齿面接触分析模型
漳河工程管理局始终坚持“以水为主、综合开发、多种经营、全面发展”的水利经营方针，以资源为依托，大力发展水利经济。
式中：
式中，h0为油膜中心处膜厚，R为综合曲率半径，E为当量弹性模量。
能量方程：
运动方程：
能量方程边界条件：
3.2.热弹流方程的求解及结果分析
3.2.1.热弹流方程的求解
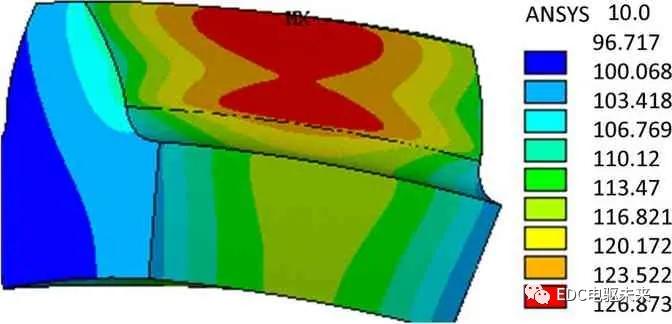
将方程(11)～(18)进行无量纲化，采用有限差分法进行离散，x方向离散成81 个不等距点，z方向离散成21 个等距点，在给定温度场情况下，求解雷诺方程，得到油膜压力和厚度分布，在给定压力和油膜厚度情况下求解能量方程，采用逐行扫描法求解温度场，将两者联立循环求解，直至得到稳定温度场。采用有限元方法求解本体温度，热平衡时润滑油温度toil=60° C，通过有限元法[8] [9]求解得到本体温度t0=396 K (1 23° C )，如图8，润滑油参数如表2所示。
Figure 8.The bulk temperature fields solved by FEM method
图8.斜齿轮有限元本体温度场分布
Table 2.The parameters of the oil
表2.润滑油参数
3.2.2.斜齿轮热弹流温度场计算结果
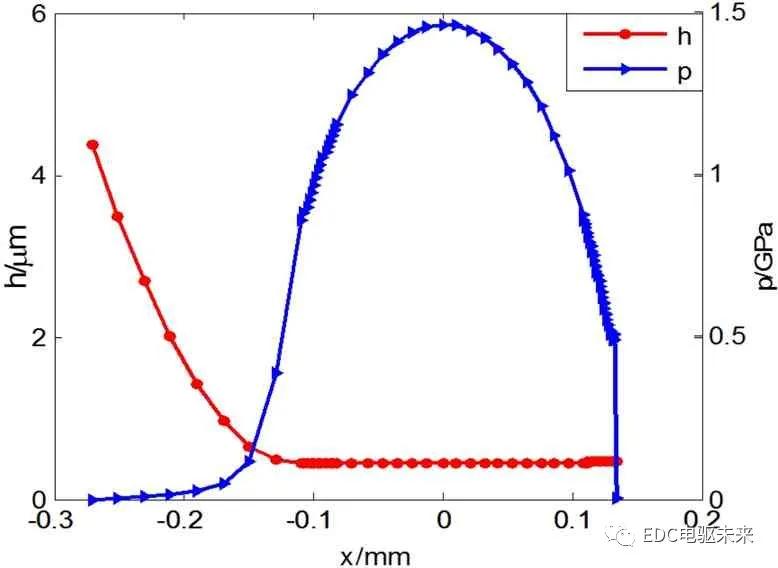
图9给出了啮入点的油膜厚度和压力分布，对于高速重载齿轮，油膜中心压力往往比较大，本例中中心压力已经达到1.45 GPa，油膜厚度约为0.4 μm，与齿面粗糙度数量级相当。由于压力较大，故压力分布和油膜分布不再具有典型的弹流特征，二次压力峰和颈缩靠近出口且很小，压力分布接近赫兹压力分布。
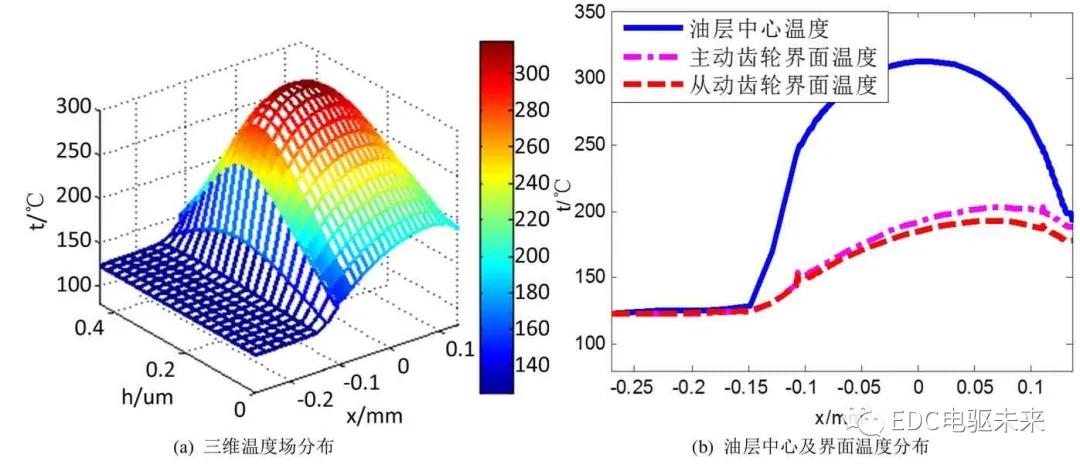
接触区的三维温度场如图10所示，(a)为三维温度场分布，(b)为中心油层和界面温度分布，可见油膜中层温度远大于界面温度，油膜中层温度分布与压力分布趋势相同，在压力最大处取得最大值，而界面温度则略有不同，温度一直升高在出口附近略有下降，取其最大值作为最高温度，其与本体温度之差为该点闪温。
Figure 9.The thickness and pressure of the oil film
图9.斜齿轮油膜厚度和压力分布
Figure 10.The temperature fields of the oil film
图10.斜齿轮油膜温度场分布
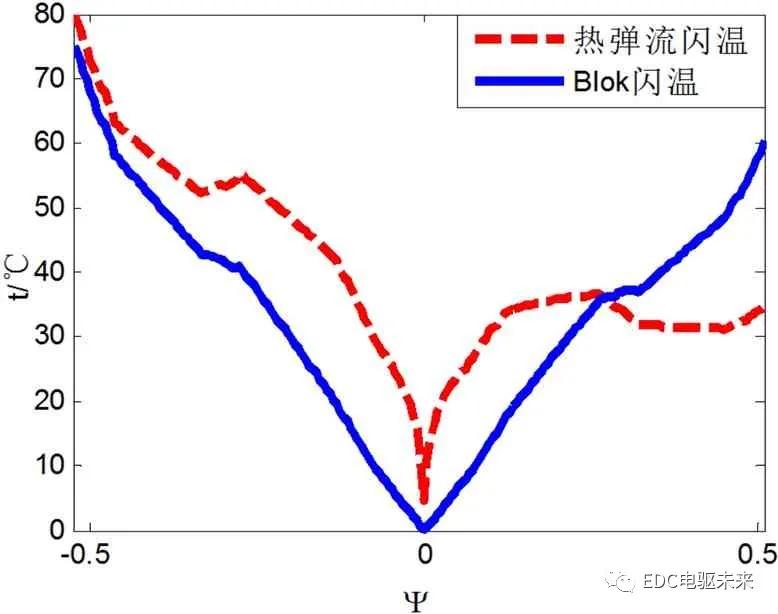
3.2.3.热弹流闪温与Blok 闪温的比较
闪温是引起齿轮热胶合破坏的主要原因，齿面高温致使油膜破裂，两齿面直接接触，摩擦系数增大，从而导致更高温度，使齿面撕裂，引起齿轮热胶合破坏。Blok 根据摩擦理论推导了齿面接触闪温公式，如式(19)。
式中，f=0.06为摩擦系数，w为单位线载荷，λi,ρi,ci,ui为轮齿热传导系数、密度、比热容和切向滑动速度，其中1、2 分别表示主从动轮，b0为赫兹接触半宽。
图11为特征坐标下的热弹流闪温和Blok 闪温的比较，两者分布趋势基本相同，在主动轮齿根和齿廓节点附件，热弹流闪温大于Blok 闪温，而在齿顶附近，热弹流闪温小于Blok 闪温。
Figure 11.The flash temperature of helical gear
图11.斜齿轮闪温分布
4.结论
1) 以端面刚度和啮合面为基础，建立了斜齿轮啮合面单位线载荷分析模型，得到了斜齿轮啮合面上每一点的单位线载荷。啮合面单位线载荷分布与转角误差趋势相同，呈方波状分布，方向与齿宽方向成βb角度，齿廓中部载荷比较大，齿顶和齿根载荷较小。
2) 建立了便于斜齿轮设计和校核的特征坐标系，既包含了齿廓信息，又包含齿宽信息，能够反映斜齿轮危险点信息，特征坐标系能够代表斜齿轮啮合面情况，可以有效地减小斜齿轮设计和校核工作量。
3) 建立了更符合实际工况的斜齿轮热弹流分析模型，得到了斜齿轮接触点的油膜厚度、压力和温度场分布，以及沿特征坐标的闪温分布，高速重载斜齿压力和颈缩靠近出口，沿特征坐标闪温大致呈V 形分布，在主动轮啮入点最大，计算结果与Blok 闪温分布规律一致，在主动轮齿根和齿廓中部，热弹流闪温大于Blok 闪温，在齿顶处，热弹流闪温小于Blok 闪温。
摘自《机械工程与技术》
- 下一篇：Robotaxi：自动驾驶赛道的排头兵
- 上一篇：纯电动载货车动力性和经济型参数设计
广告
广告
编辑推荐
最新资讯
-
氢燃料电池卡车创企“冰河时代”！HVS命悬
2024-11-17 09:45
-
小米端到端大模型：智能驾驶的“新大脑”
2024-11-17 09:44
-
阿斯顿马丁推出新款 F1 模拟器
2024-11-17 09:43
-
汽车动力电池系统试验综述
2024-11-16 08:25
-
汽车可靠性前沿技术研讨会在重庆成功召开
2024-11-16 07:33
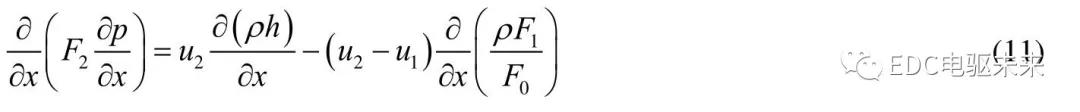
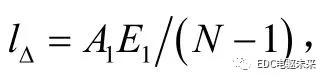
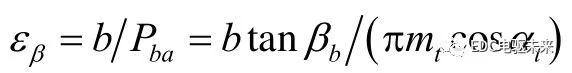
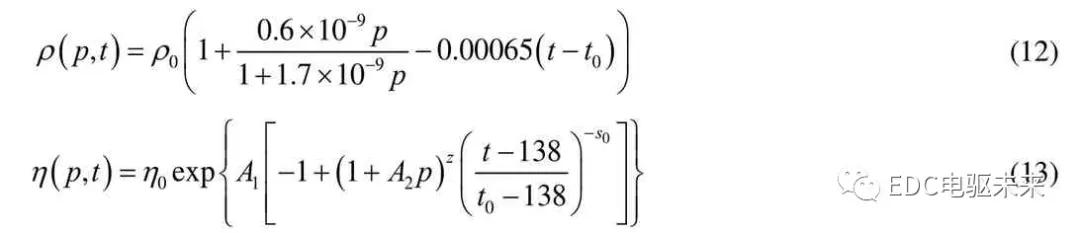
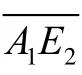
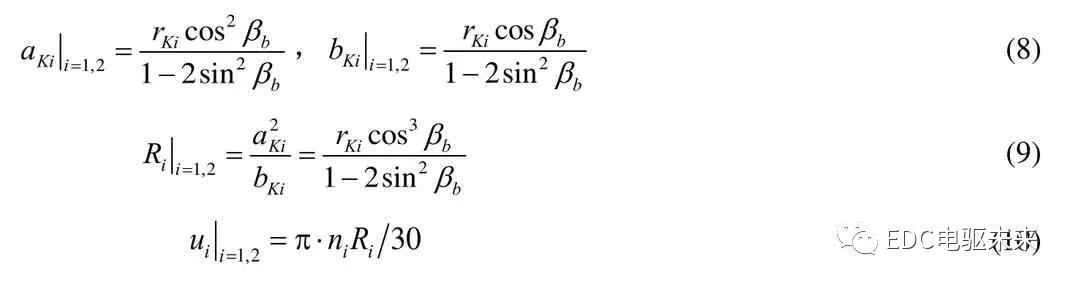
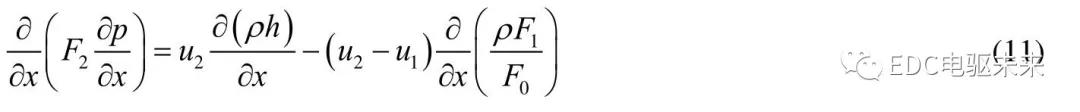
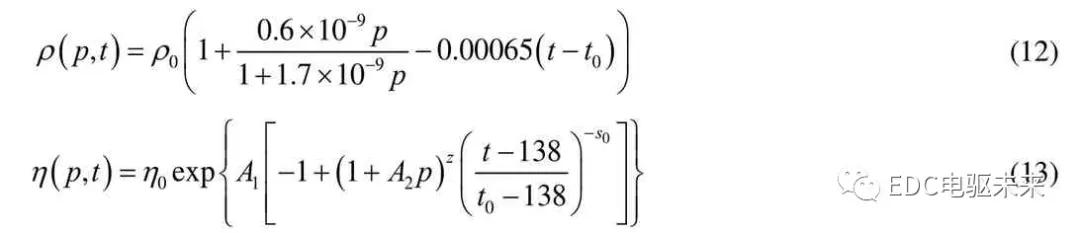
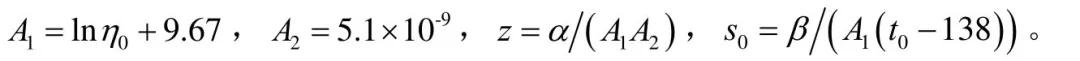
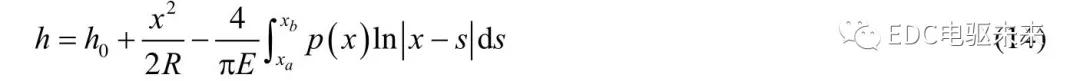
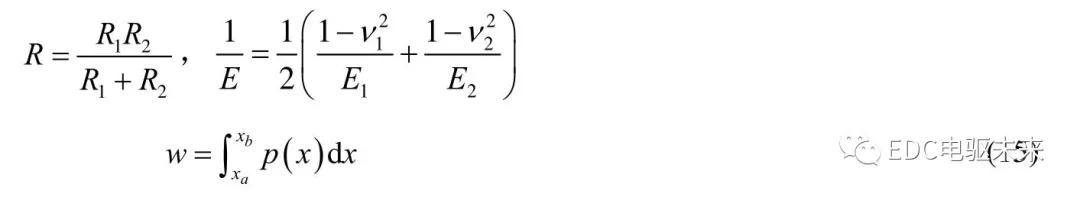
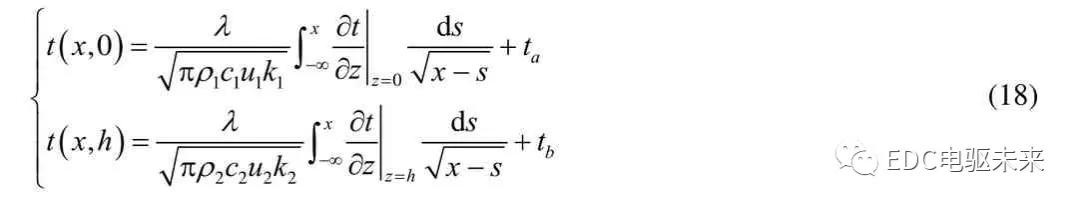
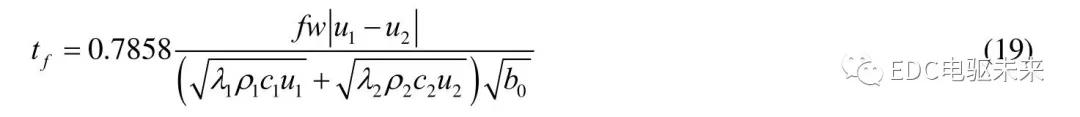
广告
广告
