广告
基于混合DDPG的车辆运动规划方法
2020-08-11 20:07:00· 来源：同济智能汽车研究所
编者按：在无人驾驶的运动规划问题中，经典的优化技术虽然性能优异，但其主要缺点是考虑到复杂的车辆动力学，在线优化需要大量的计算。人工神经网络的方法因其在
编者按：在无人驾驶的运动规划问题中，经典的优化技术虽然性能优异，但其主要缺点是考虑到复杂的车辆动力学，在线优化需要大量的计算。人工神经网络的方法因其在学习、自适应和泛化方面的优良性能而越来越受到人们的关注。作者将无人驾驶技术与机器学习结合起来，采用强化学习中DPPG的方法，设计了基于神经网络的运动规划器，其通过学习的方法来离线进行优化计算。
文章译自：
Hybrid DDPG Approach for Vehicle Motion Planning
文章来源：
16th International Conference on Informatics in Control, Automation and Robotics
作者：
Árpád Fehér, Szilárd Aradi, Ferenc Hegedus, Tamás Bécsi dand Péter Gáspá
原文链接：
https://www.researchgate.net/publication/335068669_Hybrid_DDPG_Approach_for_Vehicle_Motion_Planning/link/5ef22e2592851c3d231ebf31/download
摘要：本文提出了一种结合经典控制技术和机器学习的运动规划解决方案。对于这个任务，一个强化学习环境已经被创建，其中通过设计路径的经典控制回路提供奖赏功能。采用带有动态轮胎模式的平面单轨非线性车辆模型来描述系统动力学。通过驾驶车辆沿轨道行驶来评估规划轨迹的优劣。研究表明，这种封装的问题和环境提供了一个具有连续动作的一步强化学习任务，该任务可以用深度确定性策略梯度的学习代理来处理。这个问题的解决方案提供了一个实时的基于神经网络的运动规划器和一个跟踪算法，并且由于训练过的网络提供了对当前状态-动作对预期回报的初步估计，系统也作为一个轨迹可行性估计器。
关键词：自动驾驶汽车；运动规划；强化学习
1 前言
高度自动化驾驶和自主驾驶有望在多个方面提高道路运输质量，比如提高安全水平的同时降低油耗和排放。该课题的发展潜力使其成为汽车行业和相关学术机构最热门的研究领域之一。本文研究了可行运动规划问题，即车辆必须跟随的轨迹设计和评估问题。
许多不同的方法已经演变多年来解决运动规划问题轮式车辆，它们都有优点和缺点。几何方法从几何曲线收集车辆的路径，如螺旋线，圆弧和样条。通常的选择是将曲率定义为弧长的函数(Li et al.，2015)。它们通常用于简单的低动态场景，如自动泊车(Vorobieva et al.， 2013)。虽然这些算法的计算成本很低，但考虑车辆非完整动力学的能力受到最大转向角度和几何加速度约束的使用限制(Minh and Pumwa, 2014)。其他流行的轨迹规划方法是基于图搜索技术。将车辆的配置空间(可能状态空间)进行离散或随机采样，构建安全可达且未占据状态的图(Palmieri et al.，2016)。然后，通过一些启发式方法沿着图搜索由适当选择的度量定义的最短连接(Gammell et al.，2015)。基于图搜索的方法的制定使处理碰撞避免变得容易，但是车辆动力学的考虑仍然很难纳入。变分方法使运动规划成为一个非线性优化问题，使得几乎可以使用任意的车辆模型(Singh et al.，2017)。这些方法被证明可以生成动态可行的轨迹，即使是在高动态场景中，但是这需要很高的计算量，这通常使实时应用无法实现(Hegedus et al，2017a)。
除了传统的方法外，基于人工神经网络的方法因其在学习、自适应和泛化方面的优良性能而越来越受到人们的关注。监督学习技术用于道路车辆的运动预测(Yim and Oh, 2004)以及动态环境下工业机器人的电机控制(Liu et al.，2017)。近年来，强化学习(RL)也被成功地应用于类车移动机器人的运动规划。在(Tai et al.，2017)中，作者提出了一种移动机器人在没有先验地图信息的情况下到达指定目标位置的路径规划方法，而(Chen et al.，2017)处理行人密集环境中的运动规划。在(Li et al.，2019)中教授了跑道模拟的连续横向控制，在(Paxton et al.，2017)中，作者将MTCS方法与RL技术结合用于简单的演示。
经典的优化技术虽然性能优异，但其主要缺点是考虑到复杂的车辆动力学，在线优化需要大量的计算。
然而，随着强化学习的应用，它是有可能教会一个人工神经网络如何驾驶一个具有相同复杂程度的车辆模型的最优方式。有了这种方法，需要计算的任务就可以被转移到线下(Plessen, 2019)。本文的主要目的是建立一种针对道路车辆的轨迹规划与跟踪算法，能够在实时约束条件下提供动态可行运动。
DDPG规划提出了训练自己，用于预定义的初始状态和结束状态的最优轨迹规划问题，如3.1节所述，不考虑任何障碍，但动力学描述在3.2节。系统的输出是可由横向控制器跟踪的详细轨迹曲线。对产生的控制回路的评估考虑了角度和距离误差，并将侧滑作为可行性的衡量。
2 深度强化学习的规划方法设计
2.1 强化学习
在本文所讨论的问题中，人工神经网络(ANN)的训练缺乏训练数据，因此机器学习过程需要通过试错产生自己的经验，形成一个强化学习框架。在这个领域，学习者和决策者算法被称为代理。代理之外的一切都称为环境。环境应向代理提供以下信息:状态（输出）、动作（输入）、奖赏（输出）。学习过程由经历集组成，经历集是用一组给定的初始参数尝试解决原始问题，而经历集通常由一系列步骤组成。代理与环境进行交互，并根据提供的状态信息选择操作，从而产生代表每一步新情况的新状态。此外，环境提供了关于代理如何完成其工作的信息作为标量值，称为奖赏。
轨迹设计的发展概述如图1所示，可以看到：在每一个经历中，代理接收初始条件和轨迹规划目标并计算轨迹的内部点，然后我们驾驶车辆沿着计划路线(控制回路)，同时对其性能进行评估。学习代理收到评价后的奖赏价值之后，整个过程从头开始。这是一个一步返回的学习任务，意思是一个经历由一个步骤组成，不考虑下一个状态(图1中的灰色)，这降低了学习的复杂性。
图1:强化学习中的代理-环境交互
2.2深度确定性策略梯度方法
在我们之前的研究中，我们在车辆任务(Becsi et al.，2018)(Feher et al.，2018)(Aradi et al.，2018)中训练了强化学习代理，其中代理通过谨慎的动作控制环境，但大多数车辆控制任务和运动规划环境必须通过连续的动作来控制。我们为这种连续方法选择了一种相对容易实现但性能良好的学习代理，称为深度确定性策略梯度(DDPG)。这是一种使用深度函数逼近器的model-free、离线策略的actor-critic算法，可以在高维连续动作空间中学习策略(Lillicrap et al.， 2015)。它基于确定性策略梯度(deterministic policy gradient, DPG)算法(Silver et al.，2014)。actor μ(s|θμ)被指定为当前策略，它确定地将状态映射到一个特定的动作，critic Q(s,a)使用Bellman方程。actor通过以下规则进行更新:
3 训练环境
正如前面提到的，代理需要一个可以行动和学习的环境。这样的环境必须至少包括以下子系统:
- 基于轨迹生成模块的可行条件；
- 带有动态车轮模型的非线性平面单轨车辆模型；
- 纵向和横向控制；
- 奖赏计算；
3.1 轨迹生成
轨迹规划任务的输入包括：车辆开始时的状态和期望的结束状态。基于这些信息，学习代理决定了轨迹的中间点。
我们给出了一个训练的例子，其中位置和航向角的初始状态向量(2)固定在车辆的位置，并选择一个固定的速度(90km/h)作为主要道路的典型速度。最终状态(3)是从一组状态中提取的均匀分布的随机向量，这些状态比可行目标(3)宽一些。不可行目标的最终状态样本太多，会延长学习过程，因此需要避免，虽然有一些有利于学习边界。
通过动力学模型对规划轨迹进行了验证。可通过经验公式(4)来确定可行的最终状态，经验公式(4)给出了正常情况下一般车辆在固定速度下所能走的最小圆弧半径。通过确定初始状态和结束状态，学习代理确定了两个中间点的y坐标，它们沿着x坐标平均放置在初始点和结束点之间。考虑到初始和结束的梯度，一个样条被插入基于四个保持点，这给出了期望的轨迹。
3.2 车辆模型
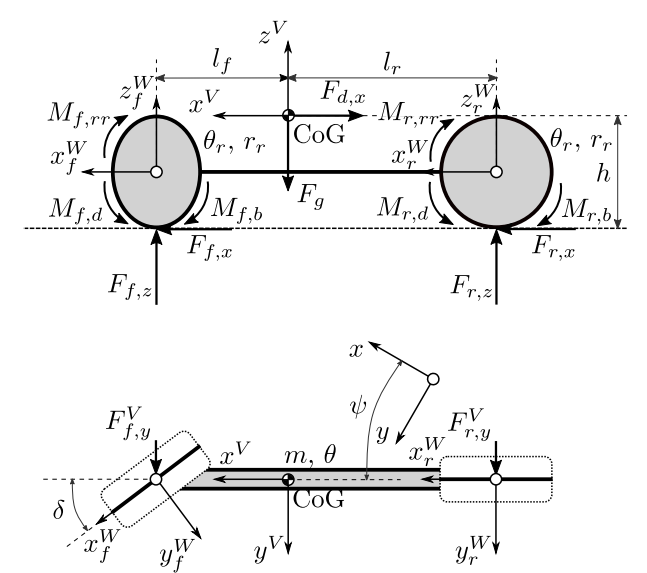
为了在合理的计算条件下准确地预测车辆的行为，采用了包含动态车轮模型的非线性平面单轨车辆模型。该模型即使在高动态驾驶动作的情况下也能给出可行的结果，但其简单程度足以使其运行时间保持在合适的水平(Hegedus et al.，2017b)。
图 2 ：非线性单轨车辆模型
多体模型(图2)包括车辆底盘和两个和前后轴刚性连接的车轮。主要参数有质量m，底盘转动惯量q，车辆重心和前后轴的水平距离lf , lr 车辆重心高度h，前后轮的转动惯量q[f/r]和半径r[f/r]。车轮模型的参数也有重要的影响，其中最重要的是摩擦系数m[f/r]，以及影响道路与轮胎间传递力的魔术公式的滑移曲线参数C[f/r][x/y], B[f/r][x/y], E[f/r][x/y]。
模型的输入是前轮的转向角(后轮被认为是无转向的)和应用在车轮上的总驱动力矩Md和制动力矩Mb(无动力系统建模)。驱动力矩通过时变分配因数xM分配给前后轴M [f / r]。对于制动力矩，理想分布为M[f/r],b，以保持相等的制动滑移。
底盘可以纵向移动x和横向移动y，并围绕其垂直轴旋转Ψ(航向运动)。车轮只能绕自己的水平轴旋转，其纵向和横向滑移率s[f/r]，[x/y]是动态建模的。下面的上标用于区分固定地面(无上标)、固定车辆(V)和固定轮(W)坐标系下的动态量，点符号(˙)用于时间导数。
利用牛顿第二定律，导出了底盘在地面固定惯性坐标系下的运动方程：
其中F为轮胎力，气动阻力的计算方法为:
其中，CD为阻力系数，Af为前向横截面积，ρA是空气质量密度。
考虑到车轮的运动，可以推导出轮胎的力。前轮和后轮的模型是平等的，所以只有方程的前面一个是提出。(Pacejka, 2012)利用牛顿第二定律建立的前轮动力学方程和动态滑移方程如下：
纵向和横向滑移相关的松弛长度为：
其中，l[f/r],0为静止的值，l[f/r],min是车轮旋转或者锁住时的值。滚动阻力矩Mf,rr按照SAE J2452的标准计算。轮胎纵向和侧向力的计算公式为:
对于力的计算，采用阻尼滑移值来提高数值解的稳定性:
式中kf, x为与速度有关的阻尼因子，计算公式为:
kf,x,0为零速度时的阻尼值，vlow为关闭阻尼时的速度。纵向力和侧向力的叠加采用拟椭圆法:
所提出的车轮模型使使用显式ODE(常微分方程)求解器(例如四阶龙格-库塔方法)具有大约1 ms的中等步长。该模型最初是用Python实现的，但考虑到学习过程中的大量迭代，即使使用了这个时间步骤，运行时也是不可行的。因此，车辆模型和求解器是用C实现的，这导致速度大约增加了10倍。
3.3纵向和横向控制
为了沿着轨迹行驶，我们开发了纵向和横向控制。在一个经历过程开始时，车辆并不是以0 km/h开始，因此为了得到稳定的状态，车辆模型使用了一个预热距离来达到初始状态。对于纵向控制任务，一个简单的PID可以有效地解决这一问题。横向控制采用斯坦利方法(Thrun et al，1970)。
Ψ是前轴的航向误差，y是前轴的横向误差，v是车速(在前轴计算，它的方向与前轮平行)，k是增益因子。
在斯坦利控制器的输出中，速度敏感饱和被应用。
3.4奖赏计算
在每个训练步骤中，代理接收到状态向量(轨迹的初始条件)并确定其动作，即中间点。为了计算奖赏，车辆通过内部的横向和纵向控制沿着轨迹行驶。训练过程的每一段经历都要持续，只要车车辆没有到达轨迹的终点，除非有终止条件使其停止。
在定义代理的奖赏函数时，考虑了以下条件，其中终止条件为:
- 横向距离误差大于10米
- 纵向或横向滑移大于0.1
- 最大步数大于2500
- (Y aw)航向角度误差大于0.2弧度
除终止条件外，滑移、角度偏差和距离偏差的总和还要求描述了该剂性能的质量特征。经历过程奖赏由三个分量组成。
环境定义了在轨迹上平均分布的10个检查点(cp)。在检查点计算距离(Rdist)和角度(Rangle)奖赏，在所有时刻计算滑移奖赏(Rslip)。定义子奖赏值在范围内[0,3]，计算方法如下:
其中，Ψ是前轴的航向误差，y是横向误差，pos是车辆在轨迹上的位置。初始值和方程是由经验决定的。当终止条件上升时，经历过程停止，代理得到负奖赏(R≈−10)。该环境包括一个重置方法，用于将车辆恢复到其初始位置。
4 结果
强化学习算法通常需要大量的迭代。培训过程的成功取决于许多参数。训练算法的超参数对其影响很大，在最近的案例中，纵向和横向控制的效率、轨迹发生器模块的可行条件和一致的奖励函数也有影响。
在本例中，最重要的超参数是actor和critic网络的学习率(αa)，(αc)和动作约束因子(af n)，(af f)和Ornstein-Uhlenbeck噪声参数(μ)，(σ)，(θ)
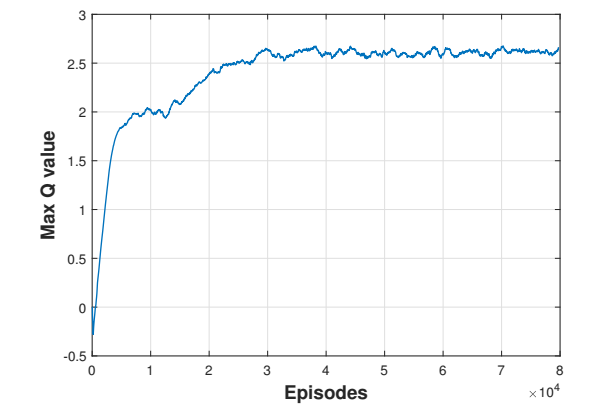
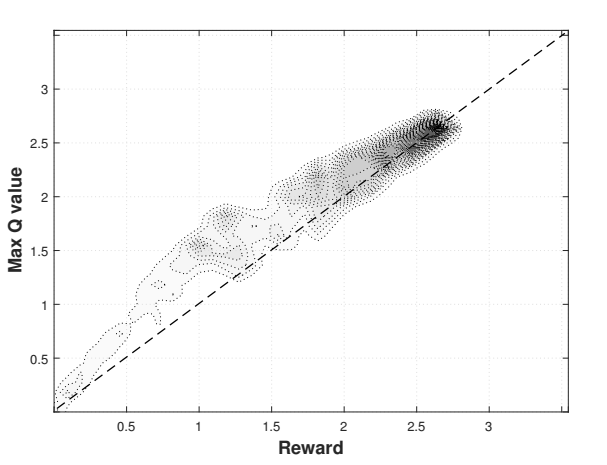
在迭代过程中，神经网络的超参数保持不变。在发展过程中，奖赏功能的形式和参数如何强烈地影响学习和结果变得很清楚。经过多次迭代后，所选择的超参数总结在表1中。下图是8万集训练后的结果。在约40000次开始产生高质量的轨迹。图3显示了使用21个经历的窗口长度的移动来平滑的最大Q值的趋势。该图显示，最大Q值稳定。critic网络很好地掌握了奖赏功能。基于密度图(图4)，学习评估几乎是完美的，它显示了估计Q值与实际奖赏的对比，从测试片段中采样。该图显示出很强的正相关关系。
图 3：训练Q值
图4：密度图
表1：超参数
对于学习智能体的性能评估，我们区分了由不同轨迹类型表示的两种情况。第一种情况(图6)为车辆需要转弯时，第二种情况(图5)为避障情况。在第一种情况下，目标角度是一个较大的值，然而在第二个情况中，它趋近于0。转弯工况的目标角度与距离有关。
图5：避障工况性能
图6：转弯工况性能
虑到之前定义的最大速度，以90km/h的车速对这些情况进行评估，测试集略大于之前认为理论上可行的区域。图表显示规划器很好地解决了这些情况。图表还表明，情况越艰难，实现的误差也越大。特别是在避障工况下，理论边界往往是有效的(见图5)。此外，除了学习的最优轨迹规划器(actor网络)之外，critic网络给出了规划轨迹的预先估计的物理可行性。对于建立自动驾驶车辆控制系统的决策模型具有实际意义。
5 结论
本文提出了一种可行的运动规划方法，并将基于深度确定性策略梯度的强化学习与经典控制方法相结合。结果表明，人工智能和经典方法的结合可以成为一个很好的工具来设计自主车辆控制的有效解决方案，其可以获得更多的可行性和稳定性的信息。该算法在学习过程中表现出收敛性，因此，经过训练的代理基本上能够生成有效的轨迹。对情况的目视检查表明代理的总体行为符合要求。进一步的研究将集中于使用变速解决方案和实际测试来扩展环境。
参考文献：
END
联系人：唐老师
电话：021-69589116
邮箱：20666028@tongji.edu.cn
广告
最新资讯
-
国外Rivian和Lucid被认为是特斯拉劲敌，而
2024-05-03 09:26
-
干货丨燃料电池低温特性测试——冷冻解冻循
2024-05-03 09:25
-
特斯拉放弃“一体化压铸”
2024-05-03 08:58
-
纯电动汽车电驱动系统功能安全技术全方位解
2024-05-03 08:54
-
动力电池行业离职率飙升
2024-05-02 17:19
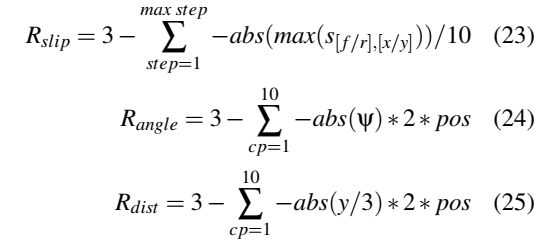
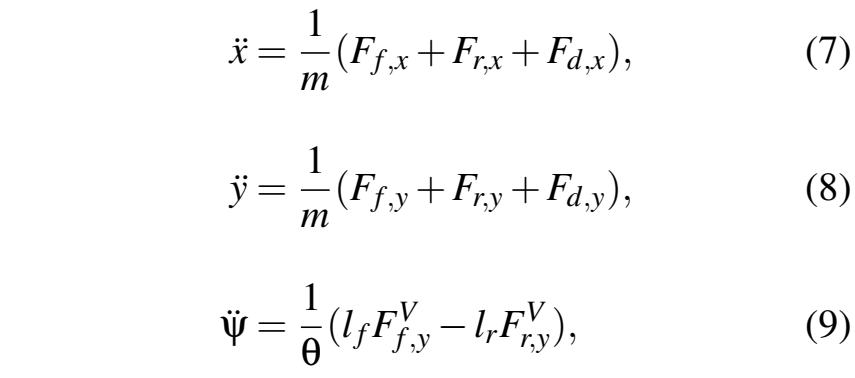
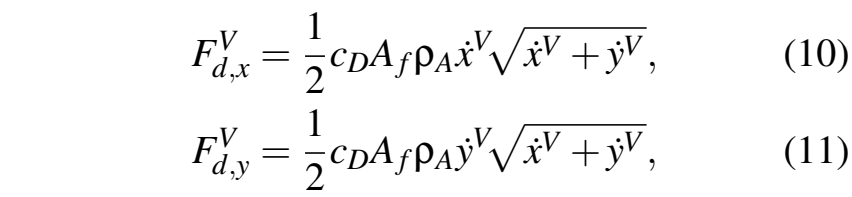
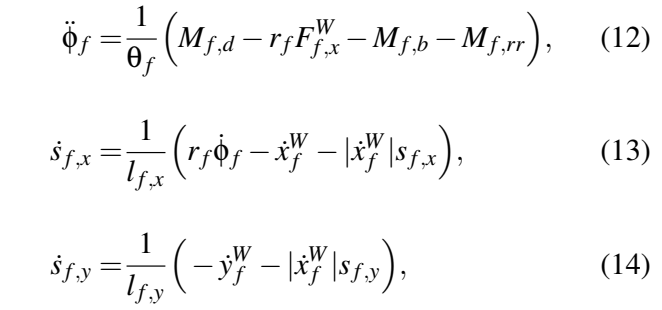
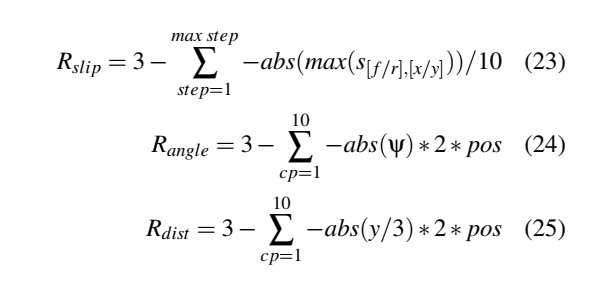
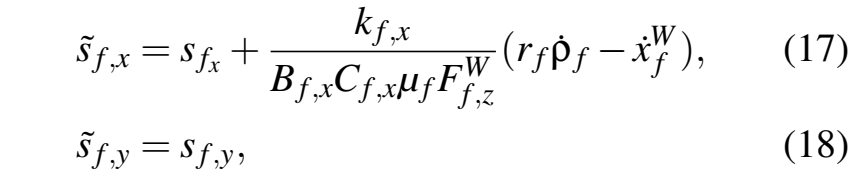
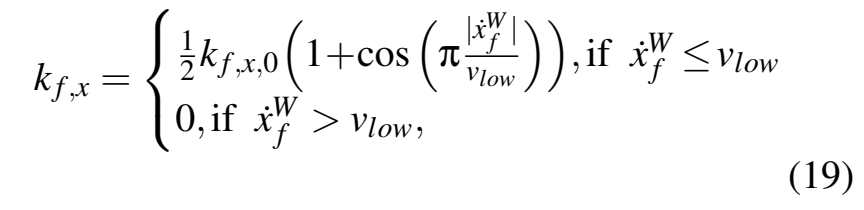
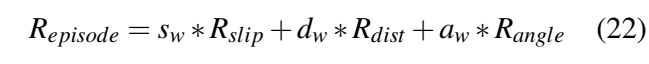
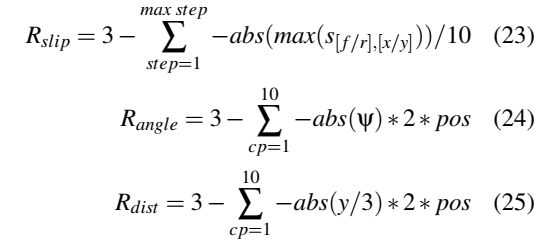
广告
广告
