变速器作为汽车重要的传动部件,其性能影响到整车的动力性、舒适性及经济性。在实际生产中,应用于汽车的变速器面临着振动大、承载能力低等问题。在驾驶过程中,司机对车辆在平稳性、经济性和长寿命等方面都提出了更高的要求,因此,改善齿轮传动系统是十分必要的。齿轮修形正是一种可有效减少载荷、平稳传动、增加齿轮寿命的途径。
1 齿轮传递系统的建模与分析
1.1 齿轮传递系统模型的建立
在Romax 中建模之前,为了节省时间并且保证Romax 模型与实际结构相符,要对结构做出一些简化,忽略一些次要因素。表1 为该减速器齿轮的4 个工况,其中加速工况3 个,减速工况1 个,由于减速工况比较简单,可采用常规的修形方法,而升速工况较为复杂,也是本文重要的优化前提。表2 为该模型的具体参数,也是优化对象。
表1 三联齿实际工况
Tab.1 Actual working conditions of triple teeth
表2 三联齿具体参数
Tab.2 Specific parameters of triple teeth
1.2 修形前齿轮的仿真分析
根据上述参数及实际工况建立模型,如图1所示。本文中因输入齿轮与输出齿轮的修形方法相同,故只涉及输入齿轮的修形。在不同工况下没有安装误差时对输入齿轮运行模拟,得到齿面载荷分布情况如图2 所示,传动误差曲线如图3所示。从图2 和图3 可以看出,各个工况下未修形时齿面偏载严重,且传动误差较大,因此齿轮在运行时振动大、噪声大,且影响齿轮使用寿命。
图1 Romax 中三联齿模型
Fig.1 Triple teeth model in Romax
2 齿轮微观几何尺寸修形
在生产加工及运行工作时,由于轴的安装误差、齿轮箱体的变形、轴承的加工误差等因素的影响,齿面受力出现偏载现象,严重影响齿轮的使用寿命。因此,从齿向修形的角度来改善偏载现象,与提高制造精度来改善齿面的偏载现象相比大大节约了成本。
齿轮系统在传动过程中,对于一对啮合齿轮,啮合齿对的工作面轮廓相互接触而产生作用力。由于轮齿相当于悬臂梁在受力时发生弹性形变,加之在齿轮生产过程中产生的齿轮误差,所以在传动过程中,实际啮合线偏离理论啮合线,造成在啮合过程中传动不平稳,特别是在啮入啮出过程中存在瞬间的波动,对系统的平稳性和寿命都有很大损害,因此对齿形修形十分必要。
常规的修形方法是通过计算公式来获得相应的量,其中齿廓的修形采用齿轮手册推荐公式
式中:Wt——单位齿宽载荷,;Ft——齿轮切向力;b——齿宽。
根据会田俊夫推荐的方法,长修形长度为短修形长度为,单位为mm。
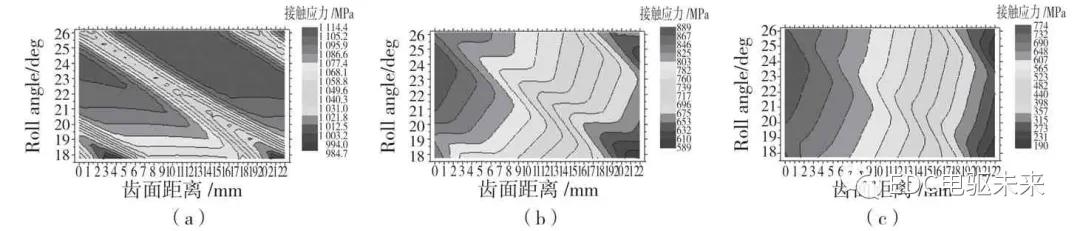
图2 3 种工况下输入齿轮未修形时接触斑点云图
Fig.2 Contact spots nephogram under three conditions before modification
(a)升速工况-479.6 N·m(b)升速工况 -298.3 N·m(c)升速工况-157.9 N·m
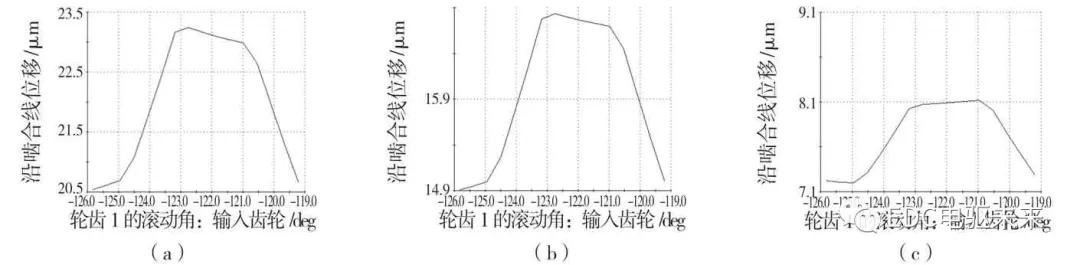
图3 未修形时3 种工况下的传动误差变化曲线图
Fig.3 Transmission error curve under three conditions before modification
(a)升速工况-479.6 N·m(b)升速工况 -298.3 N·m(c)升速工况-157.9 N·m
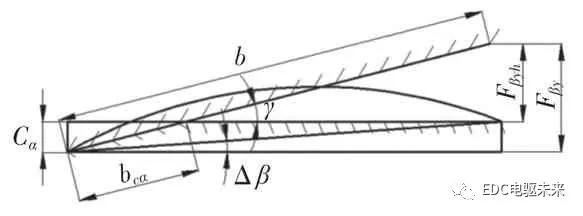
齿向修形原理图如图4 所示,齿向修形公式如下:
齿向鼓形量为
螺旋角修形公式为
图4 齿向修形原理图
Fig.4 Schematic diagram of tooth profile modification
由表1 得,在计算修形量时因扭矩不同,所得的修形量也不同,而本文中的修形旨在获得一个修形量,满足在不同的安装误差及不同的工况下修形结果都较优。通过一系列的研究,得出以下修形过程。
2.1 安装误差范围计算
齿轮进行齿形与齿向的修形前,为了让模型与实际运行时的情况相符合,将垂直方向上的安装误差等效替换到螺旋角方向上。本文讨论的模型安装误差精度为7 级,而实际生产加工中的安装误差值不好确定,且批量生产中,安装误差的值是不定的。本文给出一个安装误差的范围,在这一范围中进行修形且验证,使得在不同的安装误差下修形结果都得到优化。查阅相关资料,得7 级安装误差精度的最大值计算过程如下。
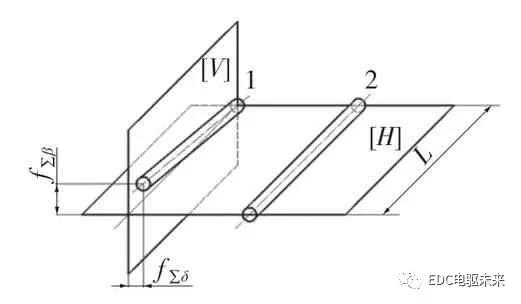
该模型中轴安装误差为垂直平面[V]上的平行度误差,如图5 所示,误差公式为
式(1)为轴上安装误差的计算公式,式(2)为轴上安装误差与反映到齿轮上的安装误差的等式关系。
两式中:f∑β——轴上安装误差值;L——轴长,L=210 mm;b——齿宽,b=22 mm;fβ——螺旋角总公差;f——反映到齿轮上的安装误差值。螺旋线总公差fβ 查阅齿轮精度标准为17μm;计算所得的安装误差f=8.5μm。所以安装误差范围为-8.5~8.5μm。
图5 齿轮副轴线平行度误差
Fig.5 Parallelism error of gear secondary axis
- 基准轴线 2.被测轴线[H]——轴线平面[V]——垂直平面
2.2 螺旋角修形量的确定
在已知载荷下,由于齿轮组加载工作时齿轮组在螺旋角方向上会产生变形且变形量固定,使得齿面产生较大的偏载现象。为了抵消这一偏载变形,通过改变齿轮的螺旋角修形量来进行补偿。螺旋角修形量的确定过程如下:在齿轮没有安装误差时,改变要修形的齿轮的螺旋角修形量,当该修形量对应的传动误差、最大接触应力最小时,该值就是所需的螺旋角修形量。
本文中模型的升速工况较复杂,有3 个工况且跨度较大。已知该模型中齿轮的偏载误差随着扭矩增大而增大,因此该模型的偏载误差在最小扭矩与最大扭矩的中间的扭矩即318 N·m下计算,并在该扭矩下进行修形。
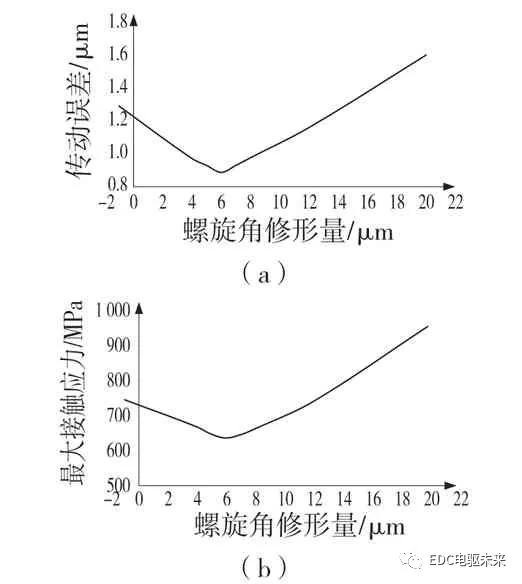
当扭矩为318 N·m 时,改变螺旋角修形量,传动误差与最大接触应力随螺旋角修形量改变的曲线如图6 所示,得到在螺旋角修形量为6μm时传动误差及最大接触应力最小,即当螺旋角修形量为6 μm 时能够较好的抵消偏载变形。
图6 传动误差与最大接触应力随螺旋角修形量改变的曲线
Fig.6 Curve of transmission error and maximum contact stress changing with helix angle
(a)传动误差随螺旋角修形量改变曲线(b)最大接触应力随螺旋角修形量改变曲线
2.3 齿向修形量及齿廓修形量的确定
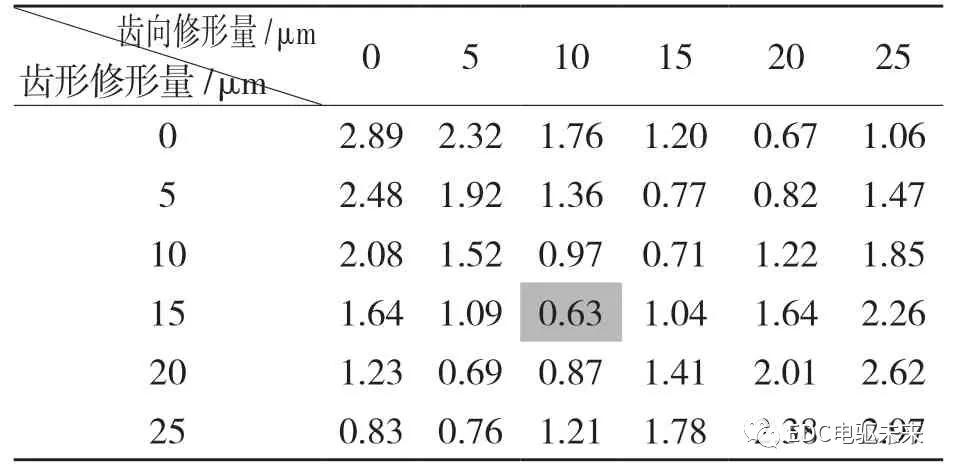
本文利用逐步逼近法先以5μm 为间隔,同时改变齿向及齿形修形量,齿向及齿形修形范围均为0~25 μm,修形范围缩小至齿向5~15 μm,齿形10~20 μm,如表3 所示。
表3 齿形与齿向修形初步结果
Tab.3 Preliminary results of tooth profile and tooth profile modification
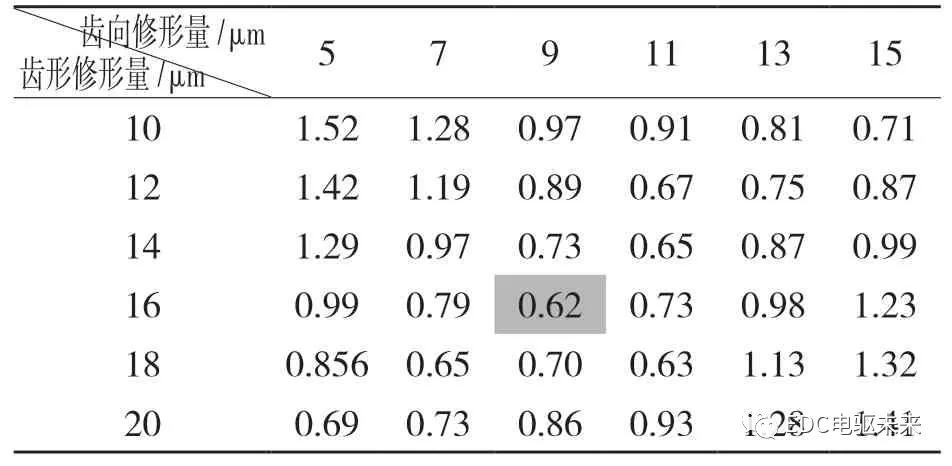
在此范围内,齿形齿向修形量间隔2 μm 继续缩小范围,修形范围缩小至齿向(7~11 μm),齿形(14~18 μm)。如表4 所示。
表4 齿形与齿向修形第2 步结果
Tab.4 Second step result of tooth profile and tooth profile modification
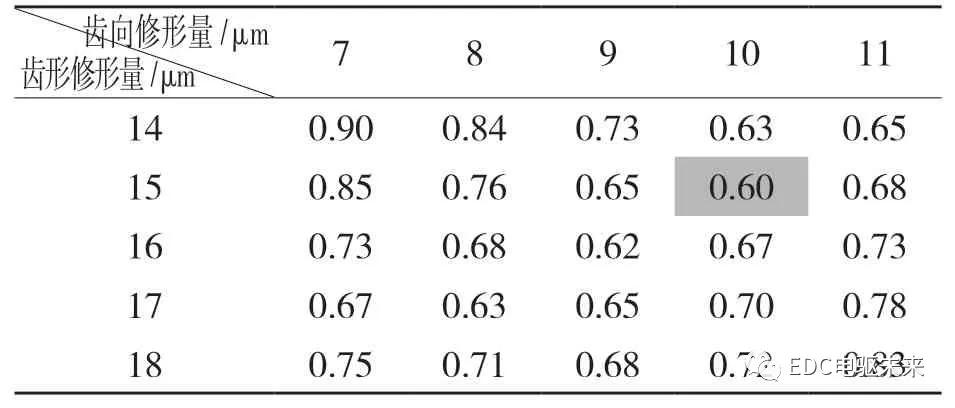
最后,齿形齿向修形量间隔1 μm 初步得到最优化修形量,如表5 所示。初步得到的修形方案为螺旋角修形量为6 μm,齿向修形量为10 μm,齿形修形量为15 μm。
表5 齿形与齿向第3 步修形结果
Tab.5 Third step result of tooth profile and tooth profile modification
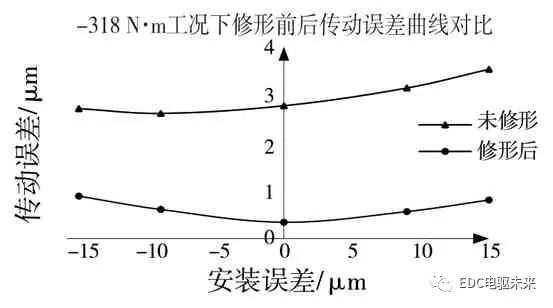
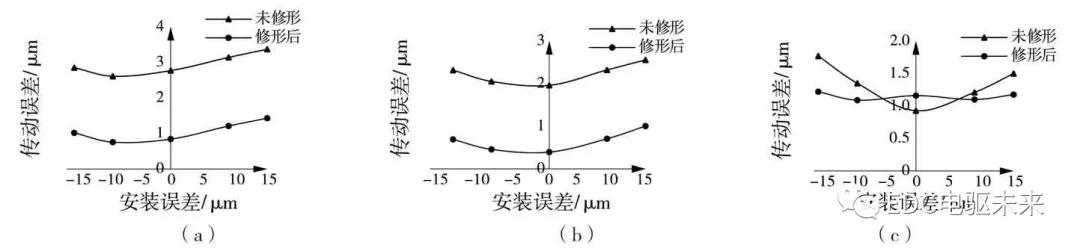
将该修形方案在不同安装误差下进行验证,比较修形前后的传动误差及最大接触应力。验证时为防超差将安装误差范围扩大至-15~15 μm,验证结果如图7 所示。
图7 工况-318 N·m 时验证修形方案
Fig.7 Verify modification plan under the condition of-318 N·m
结果表明,该修形量在-318 N·m 工况下修形结果得到优化。将该优化方案在3 种工况下改变安装误差对该修形方案进行验证,验证结果如图8 所示。
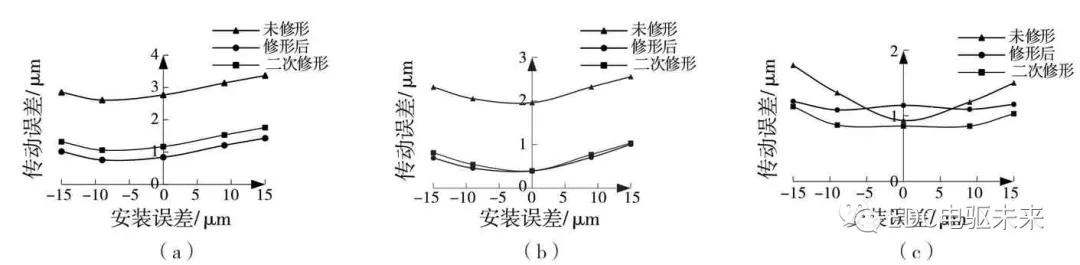
结果显示,在扭矩为-479.6,-298.3 N·m工况下修形后的传动误差都比未修形时小,但在扭矩为-157.9 N·m 工况下,安装误差-5~5 μm时,修形后的传动误差都比未修形时小,因此在扭矩-157.9 N·m 时进行微调。以1 μm 为间隔对齿形和齿向修形量进行微调,得到二次修形结果为螺旋角修形量6 μm,齿向修形量12 μm,齿形修形量17 μm,该方案在3 种工况下的验证结果如图9 所示。结果显示,虽然在大扭矩下传动误差升高了,但结果依然比未修形时好,且在-157.9 N·m 时修形结果得到优化。
图8 三种工作工况下验证修形方案
Fig.8 Verify modification plan under three working conditions
(a)-479.6 N·m 工况下修形前后传动误差曲线对比(b)-298.3 N·m 工况下修形前后传动误差曲线对比(c)-157.9 N·m 工况下修形前后传动误差曲线对比
3 齿轮修形前后对比
齿轮的传动误差是反映齿轮系统性能的重要指标之一,根据图3、图9 和图11 对比修形前后的传动误差曲线图可知,齿轮修形后在不同的安装误差及不同的工况下有效降低了齿轮的传动误差;虽然没能消除传动误差的波动,但是也大幅减少了齿间传动误差的波动范围,并且都是传动误差变化比较平缓。说明修形后,齿轮的动态性能有了极大改善。由图2 和图10 可知,对比齿轮修形前后齿面载荷分布图,齿轮修形后有效解决了齿轮啮合过程中的偏载问题。显然,修形后减少了最大接触应力,齿面载荷分布更加合理,增加了齿轮承载能力,从而增加了齿轮寿命。
图9 二次修形后在3 种工况下验证修形方案
Fig.9 Verify modification plan under three working conditions after secondary modification
(a)-479.6 N·m 工况下修形前后传动误差曲线对比 (b)-298.3 N·m 工况下修形前后传动误差曲线对比(c)-157.9 N·m 工况下修形前后传动误差曲线对比
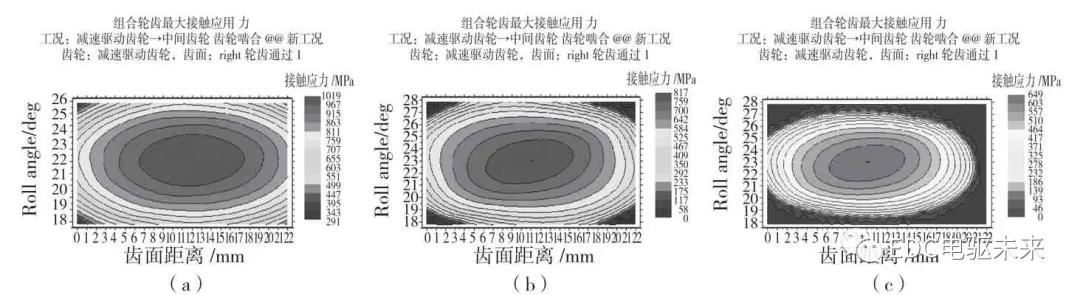
图10 修形后三种工况下的接触斑点云图
Fig.10 Contact spots nephogram under three conditions after modification
(a)升速工况-479.6 N·m (b)升速工况-298.3 N·m(c)升速工况-157.9 N·m
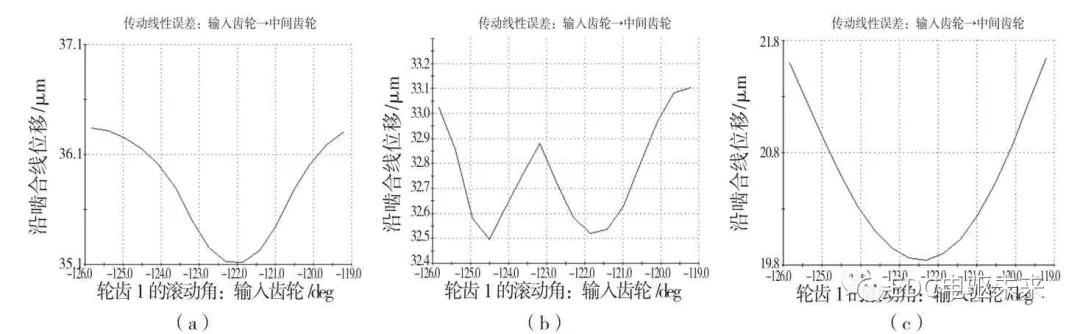
图11 修形后3 种工况下的传动误差变化曲线图
Fig.11 Transmission error curve under three conditions after modification
(a)升速工况-479.6 N·m (b)升速工况-298.3 N·m(c)升速工况-157.9 N·m
4 结论
基于Romax 平台对汽车减速器齿轮进行建模并分析。修形前的结果显示,齿轮传动时的主要问题是传动误差比较大,齿面载荷偏载严重、齿面受力不均,这三大问题导致齿轮的传动平稳性较差,齿轮的使用寿命较短。通过一系列的深入研究,本文找到了适合于不同安装误差及不同工况下较合理的修形量。由图2—图10 得:
(1)齿轮传递误差很大程度降低,从而增加了传动的平稳性,降低了振动。
(2)有效改善齿轮啮合时的偏载现象,齿面载荷分布更加合理,齿面上相同距离点的受力极差减小,增加了齿轮的平稳性。
(3)在不同的工况及不同的安装误差下,传递误差和齿面偏载问题都得到了有效的改善,从而解决了因多工况及批量生产安装误差不统一而造成的修形困难问题。
本文摘自《农业装备与汽车工程》,作者:吴晗,胡金鹏
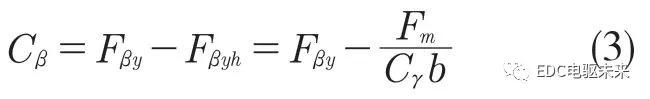


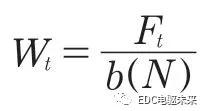

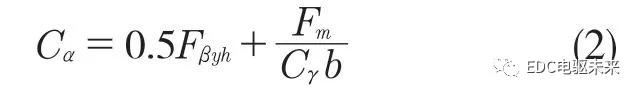
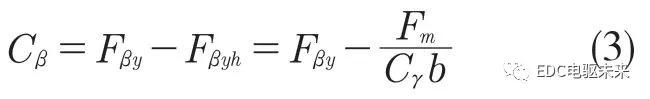
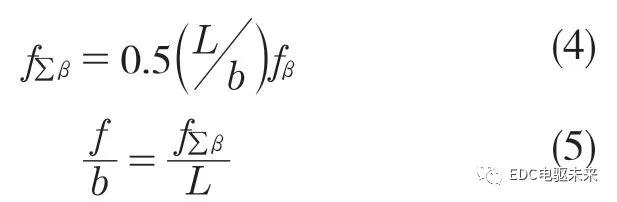





 广告
广告





























































