广告
某越野汽车磁流变半主动悬架变论域模糊控制
2020-11-04 23:22:39· 来源：ATC汽车底盘 作者：庞 辉等
摘要为了解决半主动悬架传统变论域模糊控制器过度依赖经验规则的问题，提出了一种基于模糊神经网络的变论域 Ｔ－Ｓ模糊控制策略。首先，根据磁流变减振器阻尼特
摘要 为了解决半主动悬架传统变论域模糊控制器过度依赖经验规则的问题，提出了一种基于模糊神经网络的变论域 Ｔ－Ｓ模糊控制策略。首先，根据磁流变减振器阻尼特性的实验结果，建立基于自适应模糊神经网络的减振器 阻尼力模型及１／２车辆半主动悬架动力学模型；其次，建立悬架系统 Ｔ－Ｓ模糊控制器，同时为了实时调节 Ｔ－Ｓ模糊 控制器变量的论域，采用模糊神经网络结构描述伸缩因子的变化。
仿 真 结 果 表 明，笔者提出的变论域模糊控制策 略能够有效提高车辆行驶平顺性和操作稳定性。
关键词 半主动悬架；磁流变减振器；变论域；Ｔ－Ｓ模糊控制；模糊神经网络
1.基于实验数据的ＭＲ减振器阻尼特性建模
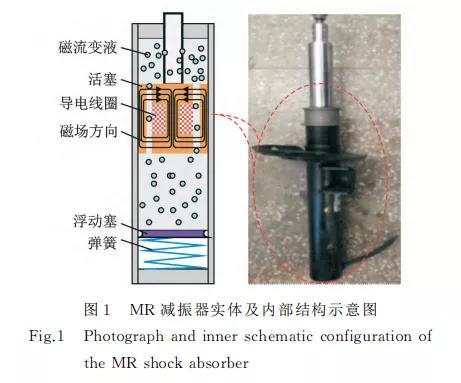
文 中选 取 路 虎 极 光２０１６款 ＳＵＶ 车 所搭 载 的 ＭａｇｎｅＲｉｄｅ减振器作为研究对象，其内部简化结构 如图１左图 所 示，图１右 图 为 笔 者 所 采 用 的 Ｍａｇ－ ｎｅＲｉｄｅ减振器实体。内部结构主要包括磁流变液、 活塞、导电线圈、浮动塞以及弹簧。通过调整导电线 圈电流大小改变磁流变液中磁性分子排列方式，进 而实现减振器阻尼力连续可调。
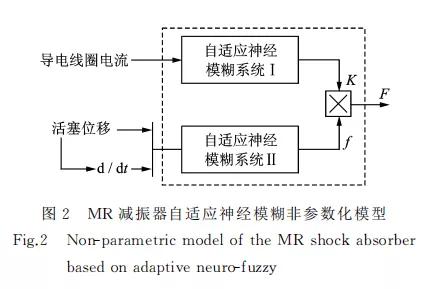
为了精确描述 ＭＲ减振器的非线性磁滞特性，学 者们研究了多种力学模型。其中自适应神经网络模 糊非参数化模型在避免大量参数识别的同时，能够较 为精确描述 ＭＲ减振器阻尼特性［２３］。其结构如图２ 所示，其中，系 统Ⅰ确 定 不 同 电 压 下 阻 尼 力 输 出 等 级 Ｋ；系统Ⅱ描述特定电压下阻尼力与活塞位移和速度 之间的非线性关系，Ｆ＝Ｋ×ｆ 为减振器输出阻尼力。
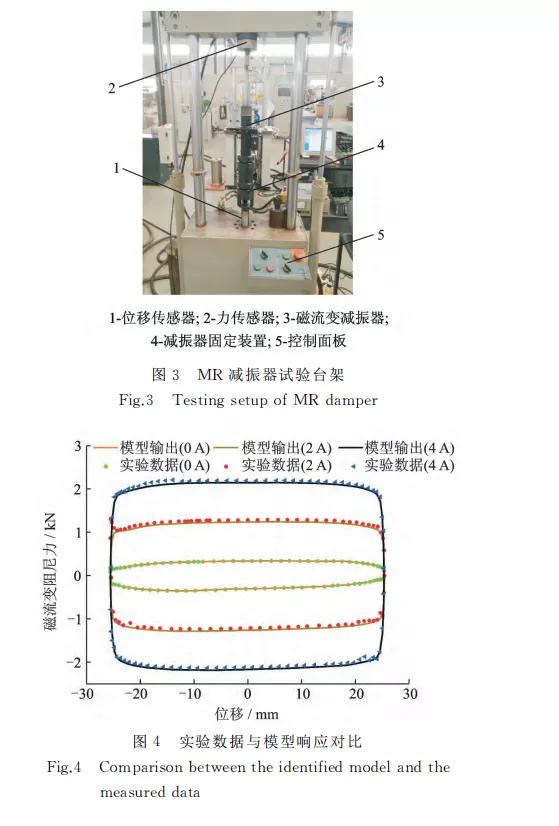
采用如图３所示的最大输出力为２０ｋＮ 的电液 伺服疲劳试验机对笔者所采用的 ＭａｇｎｅＲｉｄｅ减 振 器进行实验测试，通过分析实验数据并基于 Ｍａｔｌａｂ ＼Ａｎｆｉｓ工具箱对实验数据训练建立如图３所 示 的 ＭＲ减振器自适应神经模糊模型。
图 ４ 为 频 率 ２Ｈｚ、振幅２５ ｍｍ 时 ＭＲ减振器输出阻尼力 与活塞位移关系曲线以及对应模型仿真结果。
2.半主动悬架系统动力学模型
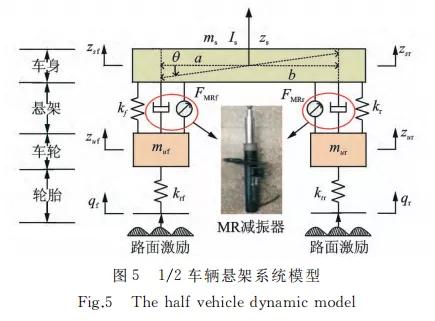
１／２车辆悬架模型包含了车辆动力学分析的主 要特征，且结构简单，所以在悬架控制策略的研究中 被广泛应用。图５为４自由度１／２车辆悬架系统模 型，其中：Ｉｓ 为转动惯量；ａ，ｂ 为前后轴到质心的距 离；θ为车身俯 仰 角；ｍｓ 为折算到半车模型上的簧 载质量；ｍｕｆ，ｍｕｒ为非簧载质量；ｋｔｆ，ｋｔｒ为轮胎刚度 系数；ｚｓ，ｚｕｆ，ｚｕｒ，ｑｆ，ｑｒ 分别为簧载质量、非簧载质 量和路面的 绝 对 位 移；ｋｆ，ｋｒ 为 悬 架的 刚 度。模 型 中用线性弹簧代替弹性轮胎，忽略轮胎阻尼；减振器 固有阻尼及可变阻尼力代替磁流变减振器，因此前 后磁流变减振器阻尼力可表示为
其中：Δｙｆ，Δｙｒ 为前后轮悬架速度；ｕｆ，ｕｒ 为磁流变 减振器可变阻尼力；ｃｆ，ｃｒ 为减振器固有阻尼。
如图５所示的１／２车辆振动模型中，要求车辆 相对于纵垂面完全对称，而且左右车轮下的路面不 平度完全一样，即认为车辆是在纵垂面上的振动，对 其受力分析如下。对于前后轴上方的垂直位移有如下关系
则悬架系统动力学方程为
３ 变论域模糊控制系统设计
３．１ 变论域模糊控制基本思想
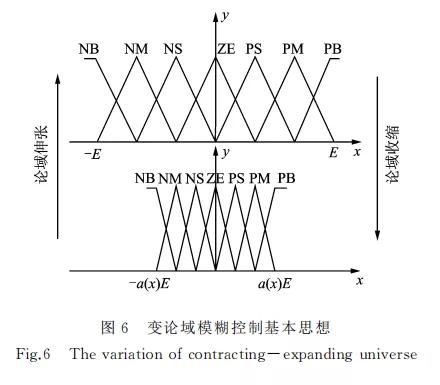
变论域模糊控制的思想可以描述为：假定 Ｘｉ＝ ［－Ｅｉ，Ｅｉ］（Ｉ ＝１，２，…，ｎ）代 表 输入 变 量ｘｉ（ｉ＝ １，２，…，ｎ）的模糊论域，Ｙ＝［－Ｕ，Ｕ］代表输出变 量ｙ 的模糊论域。同时｛Ａｉｌ｝分别表示模糊语言变 量 Ｘｉ，Ｙ 的模糊集合［２４］。具体描述如下。１）在 规 则 不 变 的 前 提 下，论域随初始论域 ［－Ｅ，Ｅ］通过 伸缩 因 子α（ｘ）变 换 为 ［－ａ（ｘ）Ｅ， ａ（ｘ）Ｅ］，如图６所 示，ａ（ｘ）为 误 差变 量 ｘ 的 连 续 函数。２）变论域的思想意味着变量 Ｘｉ，Ｙ 的 模 糊论 域随着 输 入 输 出 变 量ｘｉ，ｙ 而 变 化，具体 表 达 形 式 如式（４），（５）所示。Ｘｉ（ｘｉ）＝［－αｉ（ｘｉ）Ｅｉ，αｉ（ｘｉ）Ｅｉ］ （４） Ｙ（ｙ）＝［－β（ｙ）Ｕ，β（ｙ）Ｕ］ （５） 其中：变量αｉ（ｘｉ）（ｉ＝１，２，…，ｎ），β（ｙ）分 别 表示 Ｘｉ，Ｙ 的伸缩因子。另外，Ｘｉ，Ｙ 的初始论域定义为原始论域，且采 用７个语 言 模 糊 子 集｛ＮＢ（负 大），ＮＭ（负 中），ＮＳ （负小），ＺＥ（零），ＰＳ（正 小），ＰＭ （正 中），ＰＢ（正 大）｝。输入输出模糊论域伸缩变化如图６所示。
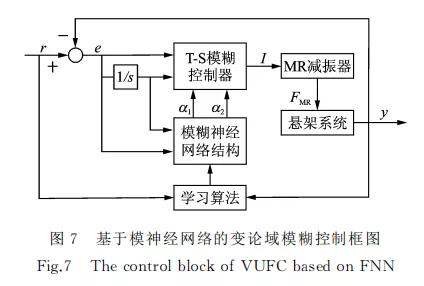
文献［２５］采 用 模糊 推 理 来 描 述 伸 缩 因 子 的 变 化，其仿真结果表明，基于模糊推理的变论域模糊控 制（ｖａｒｉａｂｌｅ－ｕｎｉｖｅｒｓｅｆｕｚｚｙｃｏｎｔｒｏｌｂａｓｅｄｏｎｆｕｚｚｙ ｒｅａｓｏｎｉｎｇ，简称 ＶＵＦＣ－ＦＲ）算法能够有效地提高收 敛速度和控制精度，但是这种控制算法伸缩因子的 模糊论域划分不够精确，从而导致控制结果存在误差。针对这一不足，笔者采用模糊神经网络结构来 控制伸缩因子的变化，结合模糊推理的语言逻辑性 和神经网络的自学习调整优势，通过系统误差分析 以及神经网络的自学习调整修正伸缩因子的模糊论 域划 分。基于模糊神经网络的变论域模糊控制 （ｖａｒｉａｂｌｅ－ｕｎｉｖｅｒｓｅｆｕｚｚｙ ｃｏｎｔｒｏｌ ｂａｓｅｄ ｏｎ ｆｕｚｚｙ ｎｅｕｒａｌｎｅｔｗｏｒｋ，简 称 ＶＵＦＣ－ＦＮＮ）框 图 如 图 ７ 所 示，ｒ 和ｙ 分别代表理想的输入和控制信号，Ｉ 表示 控制电流，ＦＭＲ为减振器输出阻尼力，ｅ 为系统控制 误差，并表示为ｅ＝ｒ－ｙ。
３．２ 基于Ｔ－Ｓ模糊模型的变论域控制器设计
Ｔ－Ｓ型模糊控制器可由如下方程组成：
其中：Ｒｉ（ｉ＝１，２，…，Ｒ）为 第ｉ 条 规则；Ｘ ＝［ｘ１， ｘ２，…，ｘｊ，…，ｘｎ ］Ｔ 为模糊 控制器的输入矢量；ｘｊ（ｊ＝１，２，…，Ｒ）为第ｊ 个 输 入 变 量；Ａｉｊ为 模 糊 集合；ｇｉ（Ｘ）为 第ｉ 条 规则 的 输 出；ｆ（Ｘ）为 模糊 控 制器的输出，采用中心平均解模糊方法；μｉ（Ｘ）为第 ｉ条规则的定义为乘积形式的满足程度；
Ａｉｊ（ｘｊ）为 ｘｊ 对Ａｉｊ的满足程度；ｈｉｊ（ｘｊ）为定义在输入论域上 的隶属度函数［２６］。文中选取车身加速度¨ｚｓ、簧载质量与非簧载质 量的相对速度ｖｒ 作为控制器的输入，控制器的输出 为半主动悬架磁流变减振器的控制电流Ｉ。对输入 变量，论 域 为 ｛－１，１｝，采 用 ７ 个语言模糊子集 ｛ＮＢ，ＮＭ，ＮＳ，ＺＥ，ＰＳ，ＰＭ，ＰＢ｝，采用高斯型隶属度函数。
Ｔ－Ｓ模糊控制器在设计过程中有两个关键性问 题：ａ．确 定 控 制 规 则 数 目；ｂ．确定规则后件的系数。确定规则数目的过程，即对输入变量划分的过程，它 需要产生合理的子空间。确定控制规则后件系数也 就是确定区域作用量的过程。
解决这两个关键问题 步骤如下。１）最优参 数。行驶平顺性和操纵稳定性是汽 车动力学研究的两个重要领域，悬架系统在协调这 两大使用性能方面起着非常重要的作用。在分析悬 架诸多影响因子中，选取３个基本参数对悬架性能 作评价，分别为车身加速度、悬架动挠度和轮胎动载 荷。为了同时满足车辆行驶平顺性和操纵稳定性的 要求，建立如式（１０）所示的目标函数Ｊ。
２）仿真过程中，以目标函数Ｊ 作为评价函数， 仿真时间３ｓ，步长０．０１，获取一组以车身加速度¨ｚｓ 和悬架相对速度ｖｒ 为输入，理想控制电流Ｉ 为输出 数据。将数据导入 Ｍａｔｌａｂ工具箱中，用自适应神经 模糊推理系统对数据进行训练，得到所需的基于 Ｔ－ Ｓ模糊模型的磁流变半主动悬架控制系统。
３．３ 模糊神经网络伸缩因子设计
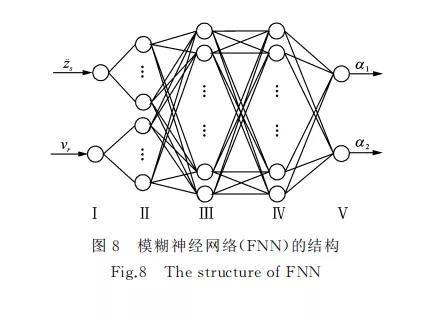
决定论域伸缩因子大小的模糊神经网络采用二 输入二输出的５层前向神经网络结构，网络的输入 节点为车身加速度¨ｚｓ 以及簧载与非簧载质量的相 对速度ｖｒ，输出节点为系统模糊控制器输入变量的 伸缩因 子α１，α２。模糊子空间均分为７个 子集，即 ｛ＰＢ，ＰＭ，ＰＳ，ＺＥ，ＮＳ，ＮＭ，ＮＢ｝。伸 缩因 子 模 糊神经网络 ＦＮＮ 的结构如图８所示。
网格的Ⅰ，Ⅱ层对应于模糊规则“ｉｆ”前提，采用 高斯型函数作为隶属函数。
其中：ｆ（１） ｉ 代表Ⅰ层第ｉ 个节点的输出 变 量；ｆ（２） ｉｊ 表 示Ⅱ层 第ｉ 个 输入 变 量 对 第ｊ 个 模糊 子 集 的 激 活 度；ｉ＝１，２；ｘ１ ＝¨ｚｓ，ｘ２ ＝ｖｒ；ｊ＝１，２，…，ｍｉ；ｃｉｊ和 ｂｉｊ分别为第ｉ个输入变量第ｊ 个模糊集合的隶属度 函数的中心值和宽度。网格的Ⅲ，Ⅳ层采用 Ｍａｍｄａｎｉ推理法实现模糊 推理。在该推 理 运 算 中，ｆ（３） ｊ 为 节点ｊ 所 有输 入 信 号的最小值，归一化运算结果用ｆ（４） ｊ 表 示。具体 计 算式如式（１４），（１５）所示。
网格的Ⅴ对应解模糊层，采用面积重心法实现 解模糊化。该 层 的 输 出 节 点ｆ （５）为调节系统模糊 论域的伸缩因子α１，α２，即
其中：ωｉｊ为ｆ（５） ｉ 的第ｊ个语言变量值隶属函数的中 心值；ｉ＝１，２；ｆ１（５）＝α１；ｆ２（５）＝α２。在实现伸缩因子调整的模糊神经网络 ＦＮＮ 结 构中，输入分量的模糊划分个数 ｍｉ 是预先确定的， 则需要学习的参数包括最后一层的连接权ωｉｊ（该层 对应于伸缩因子模糊控制器的输出论域的中心值， ｉ＝１，２；ｊ＝１，２，…，ｍ）和Ⅱ层隶属度函数的中心值 ｃｉｊ和宽度ｂｉｊ（ｉ＝１，２；ｊ＝１，２，…，ｍｉ）［２７］。
上述伸缩因子模糊神经网络是一种多层前馈网 络，因此可以采用误差反转的方法设计调整参数的 学习算法，从而使系统的实际输出逼近期望输出。设ｙｒ 和ｙ 分别表示期望输出和实际输出，定义误差 能量函数Ｅ＝１／２（ｙｒ －ｙ）２，则模糊神经网络的调 整参数的自学习算法如式（１７）所示。
其中：η＞０为模糊神经网络学习速率。为了验证笔者提出的基于模糊神经网络的变论域模糊控制算法的有效性和稳定性，使 用 Ｍａｔｌａｂ／Ｓｉｍｕｌｉｎｋ工具箱建立该控制算法的仿真 模型，在随机不平路面激励下，选 择 车 身 加 速 度、 俯 仰 角 加 速 度、悬架动行程及轮胎动载荷作为输 出 测 量 变 量。
４ 仿真分析
４．１ 随机不平路面模型
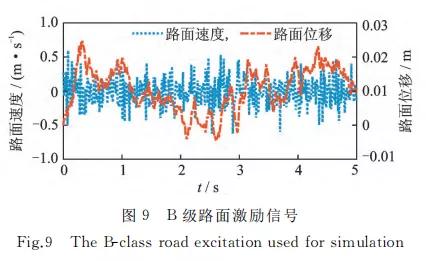
文中采用白噪声法建立路面模型为 ｑ（ｔ）＝－２πｆ０ｑ（ｔ）＋２πｎ０ Ｇｑ（ｎ０） 槡 ｕω（ｔ）（１８） 其中：ｆ０ 为路面输入的下截止频率；ｎ０ 为参考空间 的频率；Ｇｑ（ｎ０）为路面不平度系数；ｕ 为车速；ω（ｔ） 为白噪声。Ｍａｔｌａｂ／Ｓｉｍｕｌｉｎｋ仿真所得随机不平路面［２８］如 图９所示。
４．２ 仿真验证
文中仿真采用的车辆磁流变半主动悬架参数见表１。
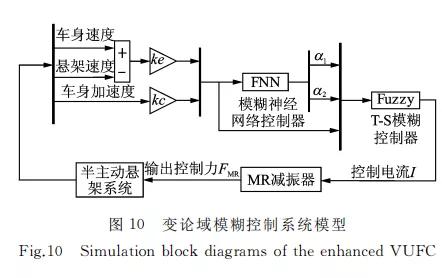
在控制仿真中，采用随机路面激励作为输入信 号，基 于 Ｍａｔｌａｂ／Ｓｉｍｕｌｉｎｋ工 具箱 的 改 进 变 论 域 模 糊控制器设计如图１０所示。
图中：ｋｅ，ｋｃ为 Ｔ－Ｓ模糊控制器比例因子；α１，α２ 为 输入变量伸 缩 因 子。ＡＮＦＩＳ采 用模 糊 神 经 网 络 控 制车身垂向加速度、车身相对速度的论域变化范围。Ｔ－Ｓ模糊控制器输出为控制电流Ｉ，同时Ｉ 作为 ＭＲ 减振器模型输入，得到控制阻尼力并作用于半主动 悬架系统。仿真条件为 Ｂ级随机路面，车速为２０ｍ／ｓ。
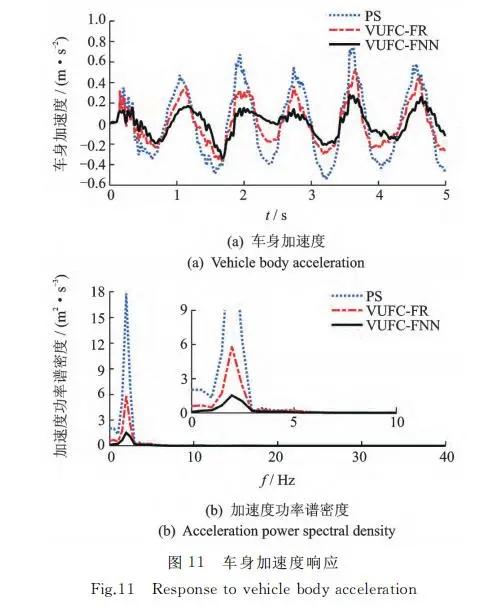
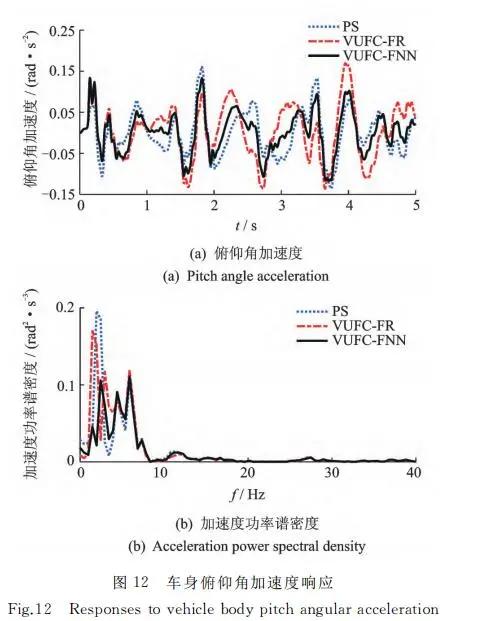
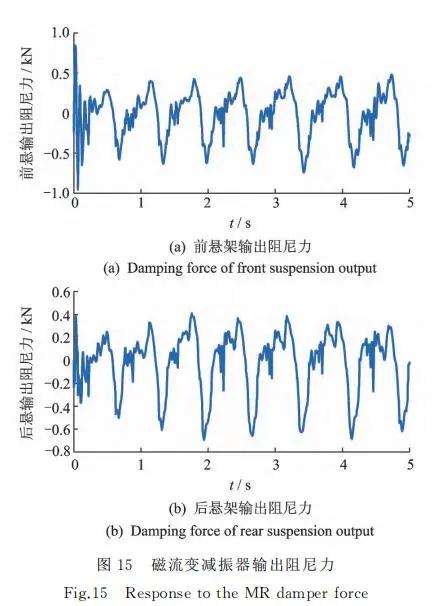
图１１～１５分别为随机路面激励下，车身加速度 ¨ｚｓ、俯仰角加速度¨θ 响应曲线及其功率谱密度分析、 悬架动行程 Δｙ、轮胎动载荷Ｆｔ 以及 ＭＲ 减振器输 出阻尼力ＦＭＲ。从图１１、图 １２ 可 以看 出，相 比 于 被 动 和 ＶＵ－ ＦＵ－ＦＲ控制悬架，ＶＵＦＣ－ＦＮＮ 控制的 ＭＲ 半主动 悬架车身加速度和俯仰角加速度优化效果明显；同时在频域响应，车身加速度和俯仰角加速度功率谱 密度也得到了较好改善。
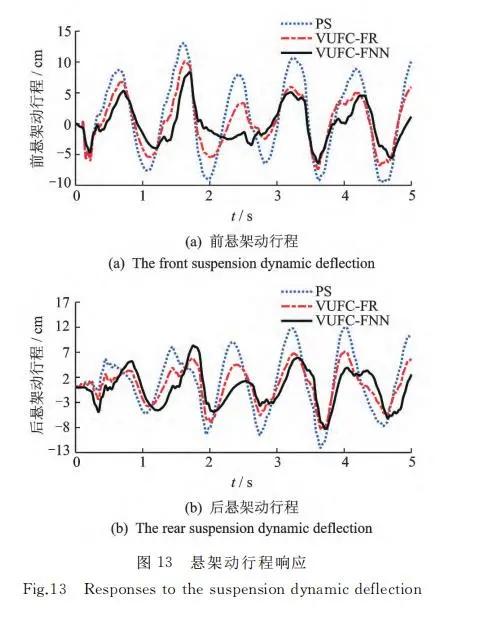
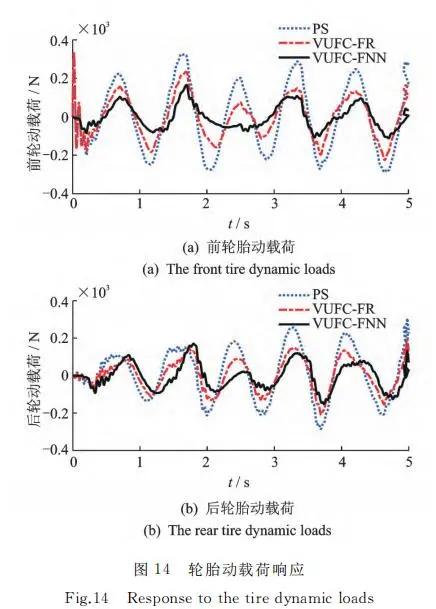
从 图１３可 以 看 出，ＶＵＦＣ－ＦＮＮ控 制算 法 可 有效减小前后轮悬架动行程，防止悬架动行程超出限 定范围而 导 致 悬 架 击 穿。从 图 １４ 可 以 看 出，ＶＵ－ ＦＵ－ＦＮＮ 控制 ＭＲ 半 主动悬架可有效改善路面作 用于轮胎的冲击载荷，提高轮胎寿命同时保证车辆 操作稳定性。图１５为前后轮 ＭＲ 减振器所产生的阻尼力。
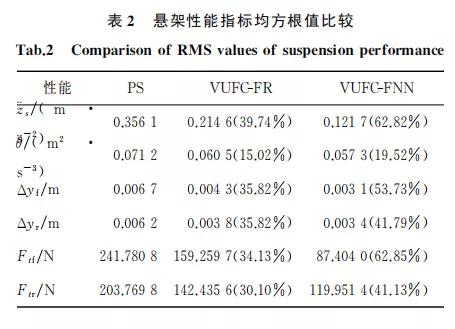
从表２ 可以 看 出，ＶＵＦＣ－ＦＮＮ 控 制 ＭＲ 半 主 动悬架在随机不平路面扰动下，各项性能指标均有 一定程度 的 提 升，而且优化效果明显优于 ＶＵＦＣ－ ＦＲ控制悬架，说明笔者所提出的 ＶＵＦＣ－ＦＮＮ 控制 算法能够有效提高车辆行驶平顺性和操作稳定性。
５ 结束语
通过建立１／２ 车 辆 ＭＲ 半 主 动 悬 架 系 统 动 力 学模型，考虑随机路况条件的影响，研究了基于模糊 神经网络的变论域模糊控制方法，并与被动悬架和 基于模糊推理的变论域模糊控制进行比较。研究结 果表明，相比于被动悬架，笔者提出的 ＶＵＦＣ－ＦＮＮ 控制 ＭＲ 半主动悬架系统各项性能指标均有一定 提 升。
车 身 加 速 度 和 俯 仰 角 加 速 度 分 别 优 化 ６２．８２％和１９．５２％；前后轮悬架动行程和轮胎动载 荷分别 改 善５３．７３％，４１．７９％，６２．８５％和４１．１３％。基于模糊神经网络的变论域模糊控制能适应路面工 况的变化，可有效改善车辆行驶的操作稳定性和乘 坐舒适性，且控制效果优于基于模糊推理的变论域 模糊控制。
文章选自：《振动、测试与诊断》
作者：庞 辉， 刘 凡， 王 延
- 下一篇：实现L5级别自动驾驶的十八层地狱闯关
- 上一篇：新能源汽车整车NVH金字塔开发流程
广告 
广告
编辑推荐
最新资讯
-
系统级封装（SiP）在新能源汽车领域的应用
2024-12-23 08:51
-
车载通信框架 --- 智能汽车车载通信架构浅
2024-12-23 08:40
-
全国首例！武汉车网智联公司完成智能网联测
2024-12-23 08:39
-
R54法规对商用车轮胎的要求（下）
2024-12-23 07:39
-
为攻克油冷技术难题，舍弗勒申请一项电机转
2024-12-23 07:38
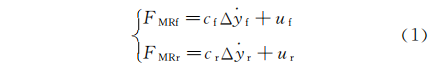
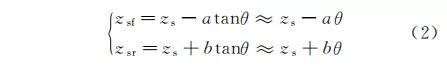
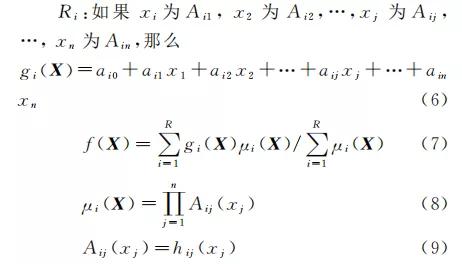
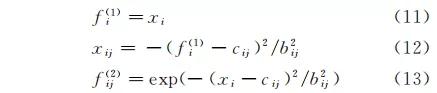
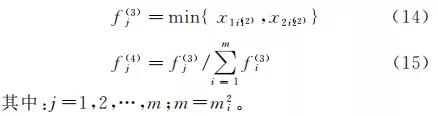
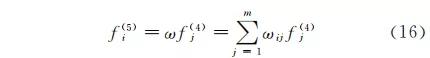
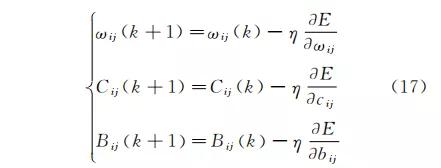
广告
广告
