广告
知识分享 | 胡克定律的解释
2022-03-23 17:09:35· 来源：HBM 测试与测量
胡克定律的解释从应变测量到机械应力，您所应该了解的。从应变测量确定材料应力在材料的弹性变形范围内，通过测量应变来确定材料应力的原理是 胡克定律。胡克定
胡克定律的解释
从应变测量到机械应力，您所应该了解的。
从应变测量确定材料应力
在材料的弹性变形范围内，通过测量应变来确定材料应力的原理是 胡克定律。胡克定律的最简单形式是:
σ= ε ⋅ Ε
σ= 材料应力 [N/mm2]
ε= 应变 [m/m]
Ε= 弹性模量, 也就是 杨氏模量 [N/mm2]
以上 胡克定律 仅适合单轴应力，双轴和多轴应力状态需要扩展版本。
注意：在应变测量中，只能确定初始条件与稍后产生条件之间的差异。初始条件可能是无负载，但也可能是预加载条件，例如物体本身的重量，如一座桥。
预加载或残余应力只能在允许的条件下进行，例如钻一个很小的孔。如果应力发生在力作用方向(0°)，也就是单轴应力状态，仅需根据上述胡克定律来计算材料应力σ。在横向（90°），尽管有可测量的应变（横向收缩，横向扩张），但不存在材料应力。因此，为了获得可靠的结果，必须知道主应力方向，并且必须在这个方向上测量应变。如果这个方向是未知的或者只是近似的，则应该以双轴应力状态进行测量和评估。
在实验应力分析的问题中，双轴应力状态应用更加频繁，不应该采用单轴应力状态的简单方法来进行;否则将会导致重大的错误。对于平面应力条件，极限法向应力 σ1 和 σ2 在垂直方向1和2上。应力 σ1 和 σ2 被称为主应力，方向 1 和 2 为应力状态的主方向。如果主应力及其方向已知，则可明确定义双轴应力条件。
例如，已知主应力方向可存在于有内压的圆柱形容器的表面上，或仅有扭转负载的轴上，弯曲的表面等。对于不同变量同时作用的作用，如法向力，弯曲，扭转等，主应力方向必须假定是未知的。双轴应力状态的主应力 σ1 和 σ2 的计算必须采用胡克定律的扩展版本，通过主应变 ε1 和 ε2，材料弹性模量 E 和材料泊松比 v 进行计算。l:
其中假定主方向3（垂直于表面）的应力 σ3 等于零。X型应变花适合已知主应力方向的双轴应力测量。应变花安装时，两个测量栅丝的方向必须和主应力方向对齐。
对于复杂形状的物体，叠加不同类型的载荷（正常荷载，弯曲荷载或扭转荷载）或不均匀性点（例如变化的截面面积），预测主应力方向通常是不可能的。在主应力的方向没有明确的情况下，必须按照下述方法进行应力分析。
在主应力方向未知条件下分析双轴向应力状态
使用应变片做实验应力分析就是用应变片测量元件表面的应变。由测量得到的应变值和已经变量（弹性模量和泊松比), 可以确定机械应力的绝对值和方向. 这些计算是根据适用于线性弹性材料弹性变形的胡克定律得来的。
在实验应力分析中，3栅应变花被用于应变测量，有 0°/45°/90° 和 0°/60°/120° 形式。用户可根据自己应用来进行选择。3栅应变花栅丝三个栅丝采用字母 a，b 和 c 表示。因此，3栅应变花测量三个应变 εa, εb 和 εc.
采用 0°/45°/90° 应变花测量
主应力 σ1 和 σ2 计算采用以下公式:
采用 0°/60°/120° 应变花测量
主应力 σ1 和 σ2 计算采用以下公式:
以下处理的目的是为实际工程师提供一种方便可靠的方法。在专业文献中描述了莫尔应力圆的理论基础。
首先计算一个辅助角 ψ 的切线：:
对于 0°/45°/90° 应变花, 采用等式
对于 0°/60°/120° 应变花, 采用等式
注意：直角三角形中的角的正切值是相反侧（分子N）与相邻侧（分母D）的比值：
下图显示，角度ψ可能在圆弧的四个不同象限中，取决于相反侧和相邻侧的符号。
这个正切的不确定性使得在对上述提及的商进行最终计算前确定分子(N)和分母(D)的符号有其必要性。确定符号的重要性在于符号能说明角度 ψ 在哪个象限。
由tan的值, 可以先确定中间角 ψ 的值：
角度 φ 需要采用以下方式确定:
在此，角 ψ 是相对栅丝 a的参考轴的数学正向（逆时针方向. 栅丝a 的轴向构成角ψ的一个臂. 而另一个臂就代表主应力方向。这是主应力σ1 (和主应变 σ1的方向相同)的方。角的顶点就是两个栅丝轴的交汇点。第二个主应力方向 (σ2 的方向) 是角 ψ +90°。
邮箱：hbmchina@hbm.com.cn
网址：www.hbm.com
免费热线电话：400-900-3165（周一至周五9:00-18:00）
广告 
广告
最新资讯
-
系统级封装（SiP）在新能源汽车领域的应用
2024-12-23 08:51
-
车载通信框架 --- 智能汽车车载通信架构浅
2024-12-23 08:40
-
全国首例！武汉车网智联公司完成智能网联测
2024-12-23 08:39
-
R54法规对商用车轮胎的要求（下）
2024-12-23 07:39
-
为攻克油冷技术难题，舍弗勒申请一项电机转
2024-12-23 07:38
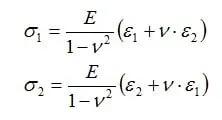
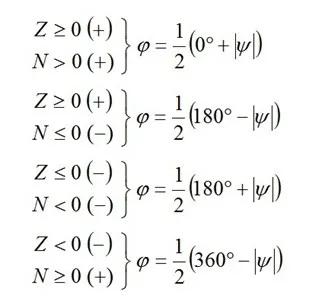
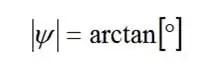
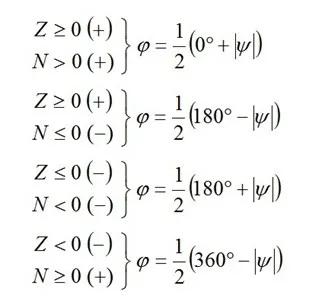
广告
广告
