小波分析

我们在进行NVH分析的时候，了解信号的频率相关分布是最基础的分析过程。常规频谱分析函数，比如FFT和倍频程等大家应该都很熟悉了。这一次我们介绍一个高级应用--小波分析，了解它的功能原理以及对比其它函数的优缺点。频率分辨率是频率相关的函数中最主要的参数，当然分析结果的时间分辨率同样非常关键。因此，下面选取的都是以时间为横坐标显示的3维函数。

首先，我们回顾一下FFT和倍频程的一些概念。

快速傅里叶变换是基于傅里叶积分的函数，信号在时间轴上进行分段（加窗），将原始信号细分为若干数据块，每块有N个样本。在平均分析中，FFT(Average)将各个数据块的结果进行平均。在时间相关的分析FFT vs. Time和FFT vs. RPM中，各个数据块的结果连续显示在3维彩图中。平均分析适用于稳态信号，而时间相关分析则是非稳态信号的首选方法。与1/n倍频程不同，FFT是一种带宽恒定的分析方法。图1表示FFT分析的频率点在线性和对数频标上的分布，可知线性频率尺度上的频率点是等距分布的，而在对数频率尺度上，频率越高频率节点之间的距离越近。其频率分辨率∆f在整个频率范围内不变，仅与采样率和分析所选择的块长度有关。


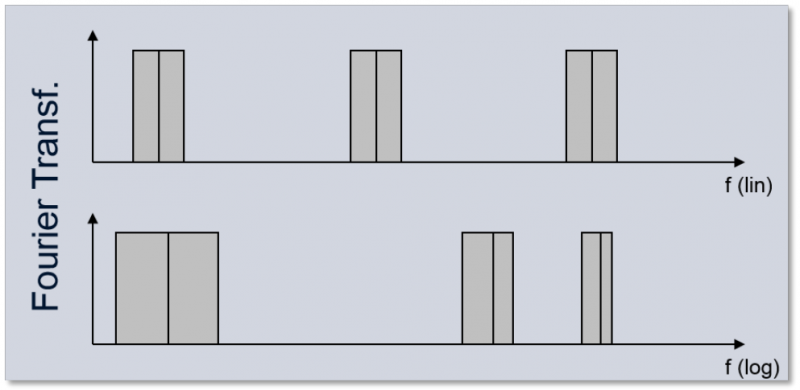
图1 FFT分析的频率点在线性和对数频率尺度上的示意图

倍频程分析将信号用数字滤波器组分割成不同频段的信号。滤波器组由多个并联的滤波器组成，每个滤波器的带宽为1/n倍频程。倍频程滤波器是指上截止频率是下截止频率的两倍的滤波器，而1/3倍频程滤波器则将每个倍频程频段进一步细分为三份，以此类推。这意味着倍频程滤波器或1/n倍频程滤波器的绝对带宽是变化的，相对带宽不变，即在对数频率尺度上，各频段等距，在线性频率尺度上显示，滤波器带宽按对数增加（见图2）。


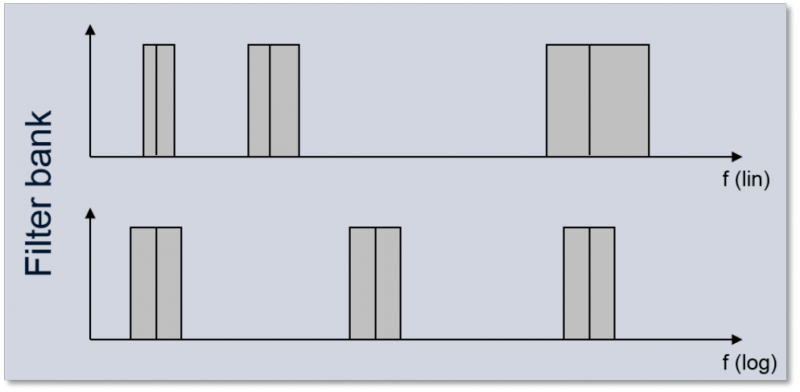
图2 滤波器带宽在线性和对数频率尺度上的示意图

中心频率为63Hz的倍频程滤波器的带宽为44Hz，而中心频率为16000Hz的倍频程滤波器的带宽为11360Hz。中心频率为63Hz的1/3倍频程滤波器的带宽只有14.5Hz，中心频率为16000Hz的1/3倍频程滤波器的带宽为3650Hz。频率越高，滤波器的带宽越大。

和FFT分析类似，1/n倍频程分析可以计算平均频谱，也可以计算与时间、转速相关的3维谱图。为此，ArtemiS SUITE提供了1/n Octave Spectrum、1/n Octave Spectrum (Peak Hold)、1/n Octave Spectrum vs. RPM和 1/n Octave Spectrum vs. Time，每个分析都有基于FFT或者滤波器两种算法。在基于FFT的算法中，不同频段是由FFT频谱中的相应频段的谱线求和计算出来的，而基于滤波器的分析则是通过数字滤波来确定频段。由于滤波法不需要对信号进行加窗处理，可以避免由此产生的能量泄露等问题，比基于FFT的结果更可取。

下面我们来了解小波分析的概念。

我们知道，傅里叶分析中用正弦波为基函数进行处理，相应的，小波分析使用称为小波的基函数对信号进行处理。正弦波仅有频率的参数，没有时间的参数（傅里叶积分的上下限是-∞到+∞），而小波基函数包含频率和时间两个参数，通过伸缩平移运算对信号逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求。在ArtemiS SUITE软件中，我们采用不同带通滤波器的脉冲响应构造小波分析函数。与分析带宽恒定的FFT不同，小波分析（就像倍频程分析一样）的频率分辨率相对带宽恒定。图3说明了FFT和小波分析在频率和时间分辨率上的区别。图中x轴代表时间，y轴代表频率。窄而高的方框代表时间分辨率高，频率分辨率低，平而宽的方框象征着频率分辨率高，时间分辨率低。

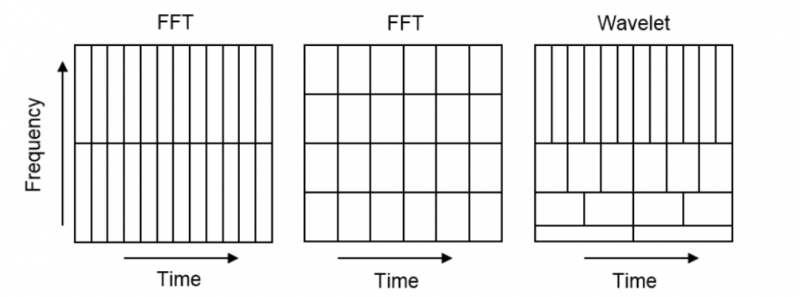
图3 小波分析的频率和时间分辨率与FFT的比较

左图和中图显示了不同窗口长度的FFT分析的时频分辨率。左图窗口长度较小，时间分辨率高，从而导致频率分辨率低。中图FFT的窗口时长大，降低了时间分辨率，但提高了频率分辨率。在整个频率范围内，FFT的时间分辨率和频率分辨率都是恒定的，而小波分析则不然，如右图所示。在低频时，频率分辨率高，时间分辨率低。向高频率发展时，频率分辨率变差，但时间分辨率明显提高。不过整个时频范围内框的面积始终保持不变。小波分析的分辨率比较近似于人耳的听觉分辨能力。

使用ArtemiS SUITE进行小波分析

图4是ArtemiS SUITE中小波分析的属性窗口。第一项用于指定频谱加权，可以设置与频率相关的加权滤波器。使用这些滤波器，不同的频率区域的权重不同。比如A计权通常用于分析空气中的声音信号。这种加权考虑了人耳对不同频率信号灵敏度的不同。


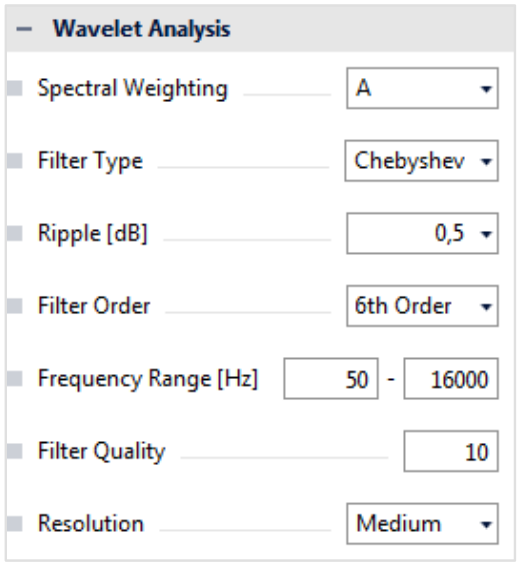
图4 小波分析属性设置

下一项是带通滤波器的参数设置，该滤波器的脉冲响应将被用作小波分析的基函数。这些参数包括滤波器类型、滤波器阶数和滤波器质量。通过这些参数定义滤波器的斜率和带宽。陡峭、狭窄的滤波器意味着高频率分辨率，但也对应了低时间分辨率。反之，平缓、较宽的滤波器意味着低频率分辨率和高时间分辨率。如果选择的是切比雪夫滤波器，则还要指定滤波器频率范围的纹波参数。在切比雪夫滤波器中，纹波会影响滤波器的斜率。在一个恒定的滤波器阶数下，接受的纹波值越大，滤波器斜率越陡。图5中蓝色实线和虚线对应不同纹波值的切比雪夫滤波器。


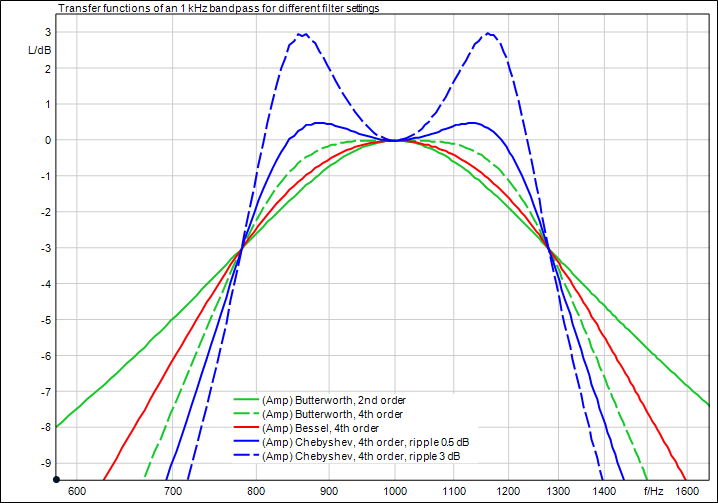
图5：不同滤波器类型的1kHz带通的传递函数

接下来设置分析的频率范围，可将分析频率限定在感兴趣的范围内。在属性窗口的最后一个选项中，可以设定所需的分辨率。高分辨率则用128个带通滤波器处理指定的频率范围，中分辨率使用64个滤波器，低分辨率使用32个滤波器。带通滤波器的数量越多，频率分辨率越好，相应的计算时间也越长。

不同分析方法对比

下面我们通过分析汽车关门声和新能源汽车电机高频阶次来比较一下不同分析方法的特点。关门声是非常短的宽带噪声，而驱动电机噪声则包含了非常明显的音调成分。为了对这些声音进行有意义的分析，不仅要选择正确的分析类型，还要选择正确的分析参数。对于关门声的分析，则需要适合瞬态数据特点，如果关心音调的各个频率，就需要比较长的数据来进行分析了。

图6为关门声的分析结果。左边的两张图是1/n倍频程分析，中间是FFT分析，右边是小波分析。图中上排和下排的区别在于计算修改了函数的某一个参数。


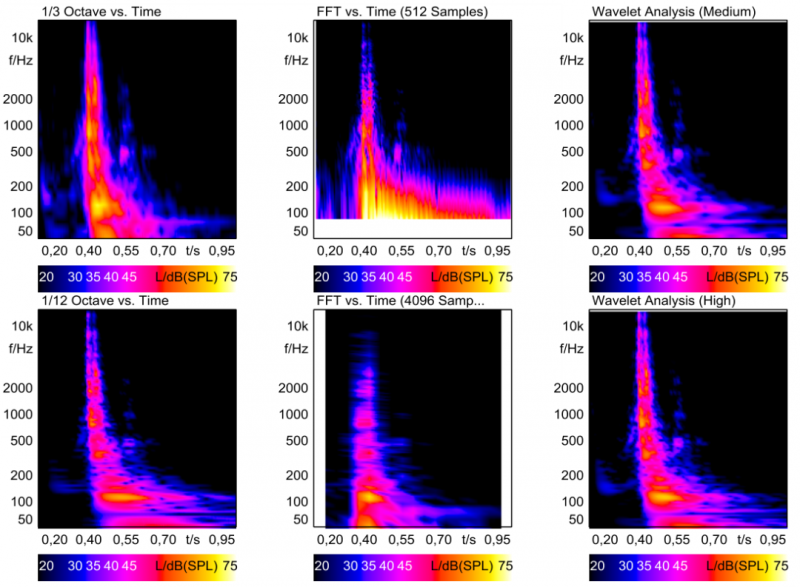
图 6 汽车关门声分析结果

不同分析函数的参数如下：
1/n Octave Spectrum vs. Time:
Band Resolution: 1/3 Octave (上) / 1/12 Octave (下)
Spectral Weighting: None
Method: Filter
Filter Order: 6th Order
Time Weighting: Manual
Manual (ms): 2

FFT vs. time:
Spectrum Size: 512 (上) / 4096 (下)
Window Function: Hanning
Spectral Weighting: None
Overlap (%): 75
Smooth: Off

Wavelet:
Spectral Weighting: None
Filter Type: Chebyshev 0.5 dB
Filter Order: 6th Order
Frequency Range: 20 to 16000 Hz
Filter Quality: 10
Resolution: Medium (上) / High (下)

从图6的对比可以看出，不同函数分析结果的频率分辨率有明显的区别。中间列的FFT分析，频率分辨率在整个频率范围内是不变的。但是，由于频率轴是以对数方式显示的，所以FFT分析的频率分辨率在低频看起来比高频差。1/3倍频程分析（左上）和小波分析（右上）一样，频率分辨率在对数频率轴上是恒定的。此外，通过比较可以看出，基于数字滤波的函数（1/3倍频程和小波分析）结果在低频时有轻微的延迟。这是由于数字滤波器的调谐过程造成的，低频滤波器的调谐时间要比高频长。而FFT分析不涉及这样的调谐，因此低频的显示并没有延迟。

图6中下排的频率分辨率更高。但是，频率分辨率的提高也有负面影响。在1/n倍频程分析中（左图），分辨率从1/3倍频程提高到1/12倍频程，导致分析结果在低频时有较强的时间混淆。在FFT分析中（中图），更好的频率分辨率（在低频时最明显）导致了非常有限的时间分辨率。而小波分析中（右图），改变分析参数的影响微不足道。

总的来说，小波分析很好地表现了关门声的时频分布。但是，如果考虑到各自分析类型的优缺点，其他两种分析类型也能揭示重要的细节。当然，最终采用哪种分析方式，还取决于用户的个人理解和实际经验。

另外，相比小波分析，FFT一个非常重要的优势是极高计算的计算效率。如果需要快速分析大量数据，或进行在线分析、实时监控，FFT将是不二之选。


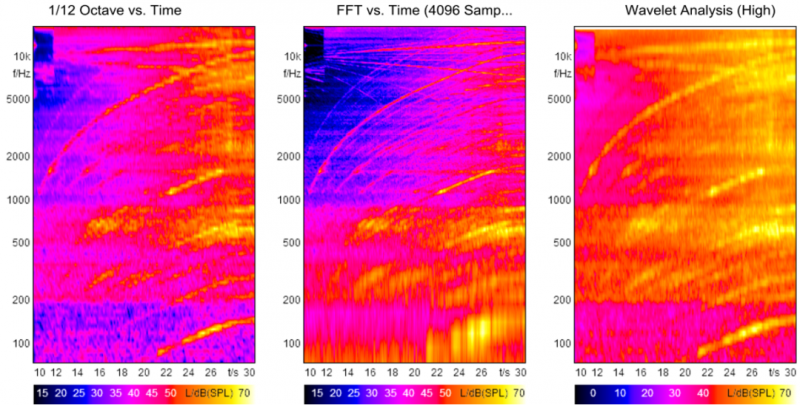
图7 新能源汽车电机噪声

包含阶次成分的新能源汽车声音的分析结果如图7所示。分析参数与图6中下排一致。可以看出，对于这种高频音调成分的分析，数据块长度为4096个样本的FFT分析特别适合，能够非常清晰地看到电机高频的阶次，以及PWM的频率。而另外两种分析方法，高频的频率分辨率则不能满足分析的要求。

在进行NVH分析的时候，不同的分析方法，能够凸显数据中不同的信息。没有一种函数能够适合于所有的数据，也不能说某些数据只能用特定的分析方法。需要了解多种分析手段，对比结合使用，才能更加深入有效的理解数据所提供的信息。