1 前言
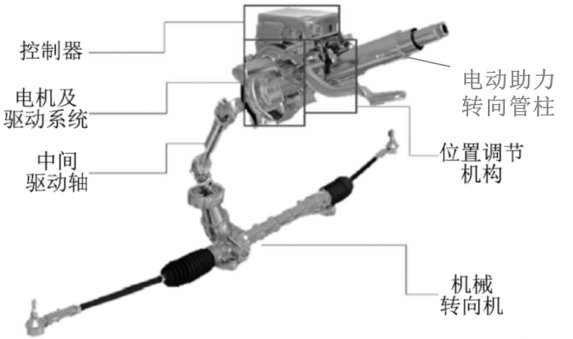
近年来,电动助力转向系统(EPS)在各车型中的应用越来越广泛,己成为转向系统市场的主体,占比达到半数以上。EPS主要由电动转向管柱和机械转向机组成(如图1所示),其中电动助力转向管柱作为传递转向意图到车轮的部件,具有减少路面传递给驾驶员噪音和振动的功能,还可以在车辆发生碰撞时充分吸能,是决定汽车行驶安全性与可靠性的关键部件,这就要求转向管柱在设计时需要同时满足严格的刚强度,模态和溃缩要求。本文重点介绍转向管柱开发过程中的结构性能及仿真。
图1 转向系统结构示意[1]
2 转向管柱模态
转向管柱的振动主要是由发动机怠速工况下产生,在城市行车过程中由于红灯、交通堵塞等经常需要停车,汽车长时间处于发动机怠速状态,如果方向盘振动过大,超过驾驶员对振动的感知阈值,会使驾驶员感觉焦躁不安。此外,若转向管柱怠速振动过大,还会引起转向系统及周边零件的振动,加速零件的损坏,影响零件之间的装配关系,从而影响转向系统正常工作。为避免电动助力转向管柱在怠速下产生抖动,电动助力转向管柱的固有频率应避开发动机怠速激振频率区间。对于常见的四缸四冲程发动机,其发动机怠速激振频率可以通过下式进行计算。
式中,f0为发动机怠速激励频率,N为发动机怠速转速,i为发动机气缸数。
发动机低频激励下转向管柱产生的结构变形形式称为其模态振型,且每一阶模态振型都对应一个固有频率,当激励与固有频率相同或相近时即发生共振。固有频率和模态振型是转向管柱的固有属性,仅与系统结构和边界条件有关。对转向管柱进行模态分析,可以得到转向管柱的固有频率和对应的模态振型。由于转向管柱结构比较复杂,一般以多自由度系统处理。对一个具有个自由度的无阻尼系统而言,它具有 个固有频率,任一瞬时的运动形态要用个独立的广义坐标来描述,系统的运动微分方程一般是个相互耦合的二阶常微分方程组成的方程组。当系统所受外力为零时,自由度系统的固有振动方程为
式中,M、K分别为质量矩阵和刚度矩阵,ü、u分别为加速度和位移向量。这个系统的固有频率为
如图2和图3所示为管柱一阶水平模态和一阶垂直模态,一般对管柱系统的模态要求为:垂直和水平的一阶模态不得低于40-50Hz,具体根据项目要求而定。
图2 水平模态振型
图3 垂直模态振型
3 转向管柱刚强度
转向管柱作为机械产品,其产品设计在一定的工作条件,如额定载荷、过载等情况下,其结构刚强度如何,能否满足在工作载荷下不发生失效破坏,不发生过大变形影响工作性能等。因此,对转向管柱结构校核是很有必要的。在满足刚强度要求的前提下,对产品进行一些优化,还可以带来诸如节省材料等经济方面的益处,有限元分析包括刚度分析和静扭强度分析。
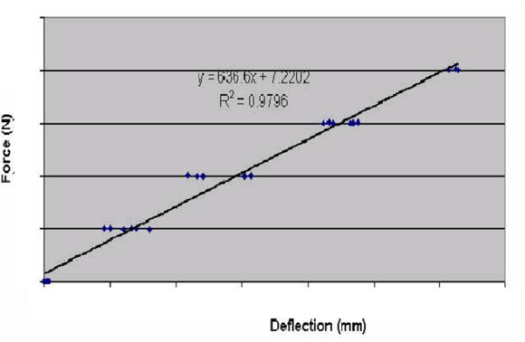
对于不同的车型和管柱结构,客户对系统有不同的刚度要求。系统刚度越高越能够迅速将驾驶员手部的转向扭矩及时准确地传递到轮胎上,获得理想的系统响应,提高用户的体验。刚度的一般测量方法为将转向管柱按照实车状态固定,在转向轴前端分别沿垂直和水平方向双向加载,并测量转向轴双向偏移的距离,获得转向管柱水平和垂直方向的刚度,并确保其均满足技术要求。如图4所示为经过拟合后的转向管柱水平方向刚度曲线,直线的斜率为平均刚度。如图5所示为转向管柱刚度分析有限元模型。
图4 转向管柱刚度曲线[5]
图5 刚度有限元模型
电动助力转向管柱转向电机安装于管柱,中间轴要承受所有的齿条力,对其强度的要求较高,此外转向管柱连接方向盘和转向机,把扭矩传递给转向机,所以在开发过程中对转向管柱有一定的静扭强度要求。静扭强度的试验方法为将转向管柱按照实车状态固定,在转向轴前端施加扭矩,并满足一定的技术要求。如图6所示为静扭强度有限元分析模型,图7为静扭强度云图。
图6 静扭强度有限元模型
图7 静扭强度云图
4 转向管柱溃缩吸能
汽车发生碰撞的过程中,汽车与外界障碍物之间发生的碰撞通常称作“第一次碰撞”,第一次碰撞发生后,人体由于惯性而发生相对于汽车的运动,与汽车内部各种机构发生的碰撞称为“第二次碰撞”。为了减少人体与方向盘发生碰撞给驾驶员带来的伤害,转向管柱一般都带有溃缩吸能机构。目前转向管柱主要通过以下4方面吸能机理来吸收碰撞能量:1.材料的弯曲, 2.材料的变形, 3.接触摩擦, 4.脱开或断开(脱钩、剪断、折断)。通常情况下转向管柱溃缩吸能结构是以上吸能机理中的综合组合形式,根据产品需要而设计,以达到最优的组合,最好的吸能效果。
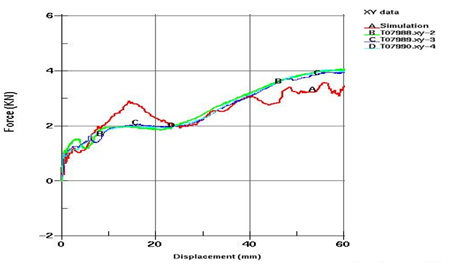
根据我国GB11557标准人体模块碰撞实验(BBT Body Block Test)中模块最大受力不得超过11123N。最大受力主要是由以下因素决定的:管柱系统的刚度、管柱系统的溃缩启动力、溃缩滑动力以及溃缩行程。准静态溃缩实验首先将转向管柱按照实车安装点安装在试验台上,使用压机以某一固定的速度压向转向轴,直到满足压溃行程的要求,并记录力与行程的关系,图8所示为溃缩力与行程的关系,图9所示为准静态溃缩有限元分析模型。
图8 力与行程的关系[6]
图9 溃缩有限元模型
由图8可知,溃缩力一般包括两部分,第一部分为启动峰值力,当压力超过某一阀值后,溃缩系统才可以启动,以避免正常工况下不必要的变形和位移。第二部分为滑动部分,滑动距离要满足最小值,滑动距离过小会增加对驾驶员的伤害;滑动力要落在某个区间,因为滑动力过小说明吸能不够充分,滑动力过大不能完全溃缩,都会对驾驶员产生较大的伤害。
5 总结
转向管柱是转向系统中的重要组成部件,其性能影响转向系统正常工作,影响汽车品质,所以采用有限元对转向管柱进行仿真分析很有必要,可以快速迭代性能,对性能进行优化,保证转向管柱的开发质量。
参考文献
[1]李谷楠,孟涛,李蓉. 机械转向机开发及优化设计[J].上海汽车,2018(12):43-46.
[2]李益. 汽车转向系统有限元分析与结构优化[D].北京林业大学,2019.
[3]汪耀,孙定凯,董正奇,孙祖明,林军.汽车电动助力转向管柱模态分析[J].汽车零部件,2020(04):47-50.
[4]张桂荣,宋新华.能量吸收式转向柱碰撞试验方法的研究[J].山东交通科技,2004(03):7-9.
[5]高明. 转向管柱吸能机构的设计与CAE分析[D].上海交通大学,2013.
[6]Tyan Tau, Vinton Jeff, Beckhold Eric, Zhang Xiangtong, Rupp Jeffrey, Kochhar Nand, Barbat Saeed. Modeling of Adaptive Energy Absorbing Steering Columns for Dynamic Impact Simulations[J]. SAE International Journal of Materials and Manufacturing, 2014, 7(2).
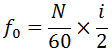
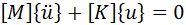
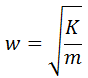











 广告
广告





























































