狭窄环境下带有多拖车的牵引车轨迹规划的统一方法

编者按：牵引车-拖车系统由于其灵活的自由度、可拆卸性、灵活的自由度等原因而得到广泛的应用。随着无人驾驶技术的发展，牵引车-拖车系统的运动规划问题引起了重视。传统的运动规划方法包括图搜索算法、基于采样的算法、最优控制算法等等，但是由于牵引车-拖车系统存在欠驱动约束和非完整约束高度耦合的复杂情况，导致一般运用于普通车辆上的运动规划算法无法处理该系统的规划问题。本文提供了利用最优控制的方法，将牵引车-拖车系统的运动规划问题转化为一个最优控制问题，为了简化数值求解过程，文中提出了一种自适应同伦热启动方法，提高了求解效率和成功率，成功解决了该复杂系统的运动规划问题。

本文译自：
Trajectory Planning for a Tractor with Multiple Trailers in Extremely Narrow Environments: A Unified Approach *
文章来源：
2019 International Conference on Robotics and Automation (ICRA)
作者：
Bai Li, Youmin Zhang, Tankut Acarman, Qi Kong, Yue Zhang
原文链接：
https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8793955

摘要：由于牵引-拖车系统的车辆运动学是由欠驱动约束和非完整约束高度耦合而构成的，因此对牵引-拖车系统的轨迹规划具有挑战性。目前流行的适用于刚体车辆的基于抽样或搜索的规划方法无法处理牵引车-拖车系统的情况。这项工作旨在处理小环境中的一般n个拖车的情况。为此，提出了一个有利于精确、直观和统一的最优控制问题。为了简化最优控制问题的数值求解过程，提出了一种自适应同伦热启动方法。与已有的序贯热启动策略相比，我们的方法可以自适应地定义子问题，使相邻子问题之间的间隙达到合适的区间来方便解算器解算。提出的自适应同伦热启动方法的统一性和有效性已经在几个极狭窄的情况下进行了研究。我们的规划方法能找到其他现有规划方法无法找到的解决方案。文中也简要讨论了在线规划的可能性。

1 引言

牵引车-拖车系统是指牵引车上挂有一辆或多辆无动力拖车[1]。通常，拖车车轮是不可转向的，转向力来自于旋转关节，这些关节依次连接整个车辆的相邻部件[2]。与等长刚体车辆相比，牵引拖车在狭窄/杂乱环境或不平坦地形下行驶更加灵活，因此在许多复杂的场景中得到了广泛的应用[3]。牵引车-拖车车辆轨迹规划是指产生牵引车和拖车从初始配置到终端配置的满意轨迹。在这里，满意度要求解决的可行性(例如，没有违反车辆运动学或无碰撞约束)和最优性(即规划轨迹预期为最优)。对于牵引-拖车车辆的轨迹规划是具有挑战性的，原因在于：（1）由于规划模型中的欠驱动约束和非完整约束耦合[4]，使得现有的大部分类车规划方法不能直接适用；（2）牵引车-拖车的动力学系统在向后运动时是不稳定的。本文主要研究了牵引拖车的轨迹规划方案。

目前流行的轨迹规划方法分为基于图搜索的方法、基于抽样的方法和基于最优控制的方法。图搜索规划方法首先将连续配置空间抽象为图中的节点，然后搜索节点之间的可行链路，使车辆被引导到目的地。Dijkstra算法[5,6]，A*算法[7-9]，采用动态规划[10]作为搜索器。与离散配置空间的基于图形搜索的规划方法不同，基于采样的规划器使用特定的状态模式来探索连续空间。State-lattice planner[11,12]和closed-loop rapid exploring Random Tree (CL-RRT)[13]分别代表了这类方法的确定性和随机性。无论是否进行空间离散化，基于图搜索和基于抽样的规划者通常都要避免直接处理整个连续的配置空间。这种思想在处理刚体车辆时可能是有效的，但对于多体车辆则有更多的挑战，因为整个系统的构型/状态是高度耦合的。一个明显的证据是，相对于针对刚体车辆的大量出版文献，针对牵引车-拖车车辆的图搜索方法或采样方法相当少。事实上，在上述已有的研究中，很少有研究能够处理受限环境下的一般n个拖车的情况。名义上，相关的轨迹规划任务应制定为最优控制问题，其中的成本函数、车辆运动学和避碰限制是明确和客观的描述。解析解由庞特里亚金最大化原理导出 [14,15]，而数值解则由非线性规划(NLP)相关优化器[1,12,16]和初始化策略[17]获得。然而，它们在有复杂障碍的情况下不起作用。除上述三类外，早期的研究还包括基于规则的规划方法，将原方案解耦成先调整航向、再沿直线[18]行走等多个步骤。这样的规划方法不够聪明，仍然不适用于不规则或狭窄的情况。总而言之，目前还没有一个统一的局部轨迹规划器，能够以可接受的计算能力来处理微小环境中的n个拖车的情况。

本文提出了一种局部轨迹规划方法，该方法能够处理狭窄/不规则环境下的一般n个拖车的情况。为此，提出了一个最优控制问题来描述该方案，并进行了数值求解。其核心贡献在于提出了一个序贯热启动计算框架，该框架简化了数值求解过程。本文其余部分的结构如下。第二节给出了最优控制问题陈述。第三节简要介绍了数值计算的基本原理。第四节提出了一种自适应同伦热启动方法以促进解决方案。仿真结果、讨论和结论将在第五节中给出。

2 牵引车-拖车系统轨迹规划问题构建

牵引-拖车车辆轨迹规划问题可转化为一个考虑运动约束、避碰约束和边界条件下的以最小化任务完成时间和最大避障距离为目标的最优控制问题。

（一）车辆运动学

牵引车-拖车系统可描述为一个牵引车拖着（n-1）个无动力的拖车的模型。由于这类系统往往在狭窄环境中移动的较慢，因此可以忽略轮胎侧滑的影响，自行车模型适用于牵引车的建模[1]：



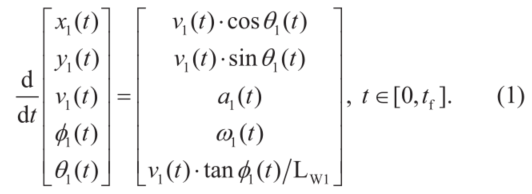
公式1中，tf 表示未知的终端时间，（x1，y1）表示后轴的中点（图1中的点P1），θ1 表示航向角，v1表示P1的速度，a1表示对应的加速度，φ1 是前轮转角，ω1是对应的角速度，Lw1表示轴距，LN1表示前悬长度，LN2表示后悬长度，LB1表示牵引车宽度。


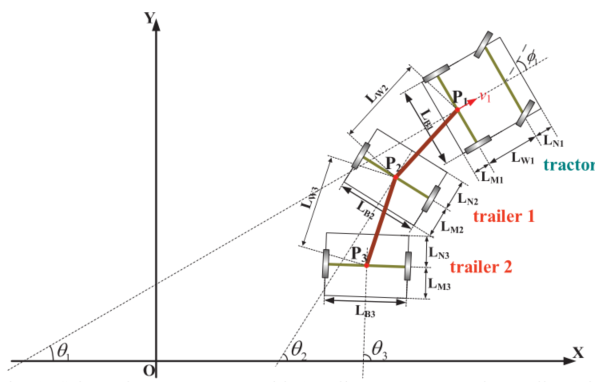
图1 以有2个拖车的系统为例的牵引车-拖车系统模型

拖车的运动学原理可描述为：

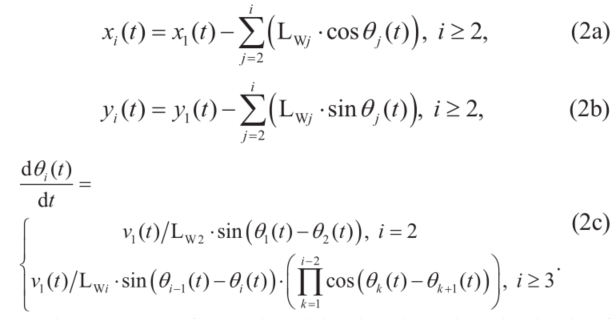
这里，（xi，yi）表示第i个部分的轮轴中点。Θi 表示第（i-1）个拖车的航向角，Pi表示连接第i个部分和第（i-1）个部分的连接点。每两个相邻的连接点 Pi和Pi-1都通过长度为Lwi（i≥2）的刚性连接相连。图1中描述了LBi，LMi和LNi的定义。边界条件如下：



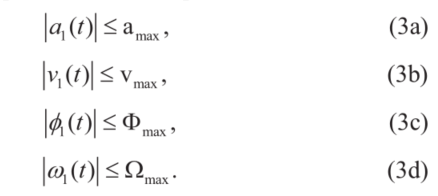
为避免涉及折刀效应[19]，对牵引车-拖车系统的两个相邻部分之间的航向角之差进行了界定:



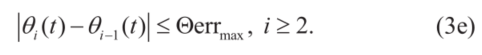
（二）避障约束

假设每台牵引车/拖车都是矩形的，环境中的每一个障碍物都被表示为一个凸多边形(凹多边形可以解耦为多个凸多边形)。在t∈[0,tf]过程中，每一辆拖拉机/拖车和每一个多边形障碍物之间的碰撞都应该避免。设第j个多边形障碍的第k个顶点为Vjk(k=1,2，…Npolj)，将车辆第i部分的四个顶点表示为Ai、Bi、Ci和Di (图2)。


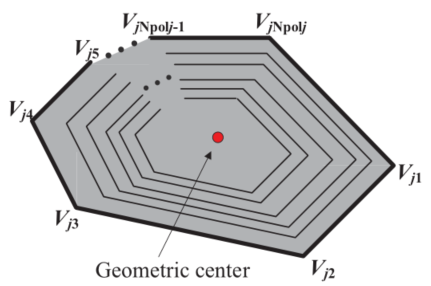
图2 矩形牵引车/拖车和凸多边形障碍物的顶点示意图

车辆第i个部分与第j个障碍物之间的避障约束为：（i）Ai、Bi、Ci和Di位于第j个凸多边形之外；（ii）每个顶点Vjk位于矩形Ai、Bi、Ci和Di之外。一点Q位于一个凸多边形W1W2…Wm之外的条件可通过“三角形面积准则”不等式来描述：


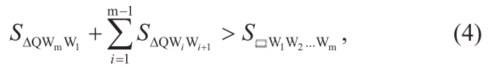
式中，表示三角形面积，表示多边形面积。根据公式（4），前面的约束条件（i）和（ii）可表述为：



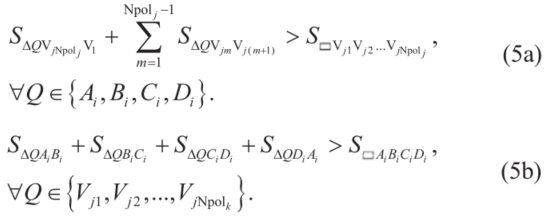
将（5）在[0, tf]之间对每个牵引车/拖车和障碍物之间进行应用，就能以完整的形式表达避障约束。

（三）边界条件

在起始时刻t=0，整车状态(包括x1(0), y1(0), v1(0), φ1(0),θ1(0),a1(0),w1(0), θ2(0)等)。在终端时刻tf，期望车稳定地停在期望的位置。这里，稳定性是指



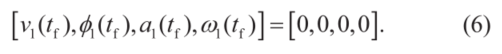
若没有式（6）的约束，车辆无法在t> tf时稳定地停止。

（四）目标函数

我们希望车辆在最短的时间内完成行程，并在整个过程中与障碍物保持最大的间隙。因此，代价函数J被定义为


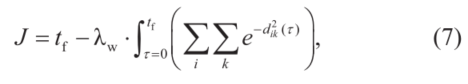
这里，表示时刻（xi，yi）与第k个障碍物几何中心之间的欧氏距离。，是权重参数。

（五）最优控制问题

综上，整个优化控制问题可以构建如下：


式（8）中的未知量包括

3 最优控制问题的数值解法

由于避碰约束(5)的复杂性，一般无法得到(8)的解析解。相反，我们期望得到数值解。通常，数值求解(8)包括两个步骤:（i）离散化所有的状态空间，建立一个NLP问题;（ii）求解转换后的NLP问题。本文采用一阶显式龙格-库塔法进行离散化，采用内点法[21]求解NLP解。

4 NLP的简化解法

（一）动机

简单地应用第三节中的方法并不能得到通用情况的最优解，因为复杂的避免碰撞约束(5)很难由IPM或其他基于梯度的优化器直接处理。简化计算负担的一种常用方法是找到一个接近最优或甚至接近可行的初始解，从这个初始解开始求解nlp过程[17]。根据这个想法，我们可以定义一个子问题序列，使第i个NLP解总是比第（i-1）个子问题复杂，最后一个子问题是原问题，即离散化问题(8)。由于第i个子问题比（i-1）个子问题复杂，因此子问题（i-1）的最优值是子问题i的一个接近可行的初始解。如果我们找到子问题1的最优解，那么序列过程将在有限周期后得到原问题的最优解。前面提到的顺序过程本质上是为了避免一次性处理所有的困难。相反，整个困难分散在子问题中，然后逐步解决。理想情况下，离散应该保证每个子问题的递增的难度是相同的。然而，在顺序计算过程真正开始之前，几乎不可能做到这样的离散度。

为了解决上述问题，一个自然的想法是在顺序过程中自适应地调整子问题的分散水平。例如，当子问题k无法解决时(即优化过程收敛到不可行或不收敛)，则表示子问题k与k-1之间增加的难度太大，因此进一步的难度分散需要施加。这使得更多的子问题将在子问题k与k-1之间被创建并求解。另一方面，如果连续的子问题已经被解决，这可能表明相邻子问题之间的间隙非常小，那么我们将尝试跳过序列中的一些子问题来加速计算。下一节将详细介绍自适应色散策略的原理。

（二）自适应同伦热启动方法

自适应同伦热启动方法的特点是解决一系列子问题，其中，首先缩小障碍，然后自适应地扩大到其标称大小。

标量用来调整每个障碍物的尺寸（图3）。假设第j个多边形障碍物拥有Npolj个顶点，即：，那么几何中心图片可表示为：

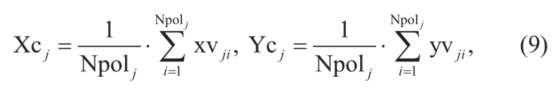
其中为顶点i的坐标。一组新的顶点集合就可以用来表示：



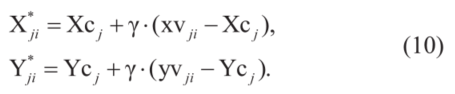
根据公式（10），新多边形大小就会随着单调变化。当图片=1时，新的多边形就等同于原来的障碍物；当=0时，新的多边形就缩小为几何中心。如果我们在NLP问题中将每个障碍物用代替，那么我们可以通过简单地调整，使其从0到1单调变化，以此来定义一系列不同的子问题，即从简到繁。

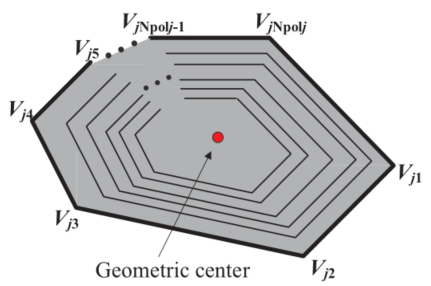
图3 同伦障碍物的示意图

自适应同伦热启动方法的目标是找到合适的增量步骤让从0到1变化。最开始，最简单的子问题是即子问题0)，其中接近于0+。如果最简单的子问题0无法解决，则取消后续程序;否则我们设置达到，然后开始顺序计算。在循环1，一个新的子问题(即子问题1)以进行建立。在数值求解子问题1时，所记录的最优值作为初始解。如果成功地解决了子问题1，那么就实现了更新，，并记录子问题1的导出的最优解以供将来使用。反之，如果子问题1无法解决，那么step只需将其值降低为。这个迭代过程一直持续到时问题圆满解决。在迭代过程中，如果成功地展开了个连续子问题，则步长增大为。当step小于预定义的阈值时，则整个迭代计算过程终止。该方法的伪代码如下。

算法1 自适应同伦热启动算法


5 仿真结果和讨论

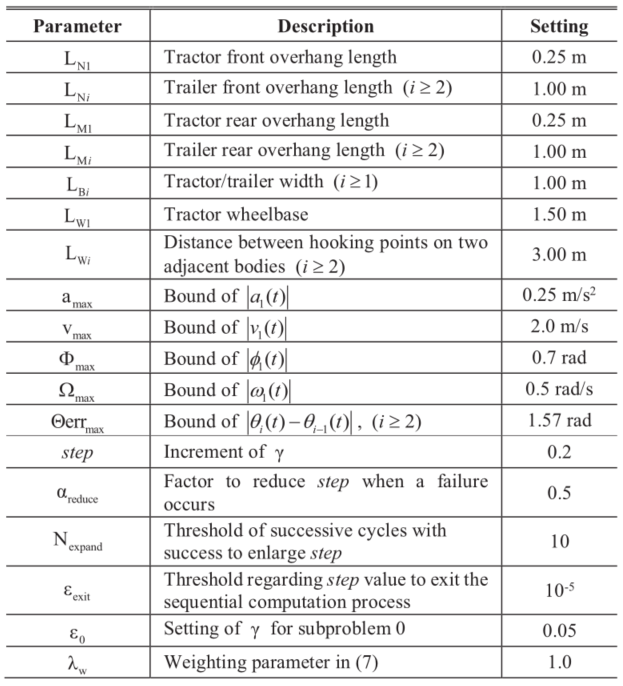
仿真在MATLAB+AMPL平台[22]上进行，并在2.50×2GHz运行速度为8GB RAM的i5-7200U CPU上执行。关于车辆和算法1的常用参数见表1。

表1 关于模型和方法的参数设置


（一）算法1的效率

对三种情况进行了测试，优化轨迹如图4 - 6所示。案例1的场景中有一个由两个不规则放置的障碍物构成的瓶颈。在图4中，整个系统的任何部分都没有与障碍物发生碰撞，这说明我们的公式(5)是有效的。案例2涉及到一个杂乱的环境。观察情形2的最优解(如图7所示)，可以发现牵引车的轨迹比每一辆拖车的轨迹复杂，拖车i的轨迹比拖车i+1的轨迹复杂。这一现象背后的原因已经在[1]中进行了分析。这种现象也反映在案例3中，这是一个典型的车库-停车场方案。在本小节结束之前，让我们以案例1为例，研究一下算法1的顺序计算过程。如图8所示，在最终解决原NLP问题之前，共解决了40个子问题。在顺序过程中，无论何时停止增加，出现问题，然后step减少。另一方面，step仍有增加的机会(见其在20 ~ 25周期的短暂增长)，这意味着扩展的相关准则生效。综上所述，算法1能够有效地处理各种情况。


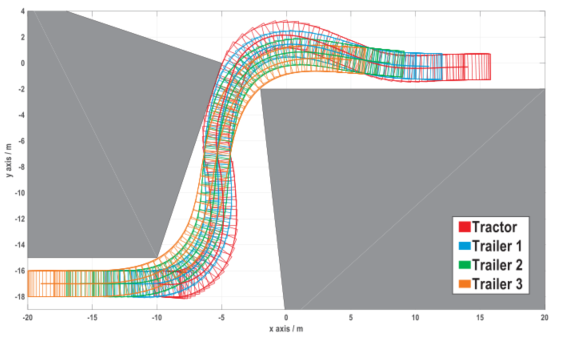
图4 案例1中优化的轨迹和对应的足迹(CPU时间为334.10秒，tf =28.57秒)


图5 案例2中优化的轨迹和对应的足迹(CPU时间为114.24秒，tf =32.07秒)


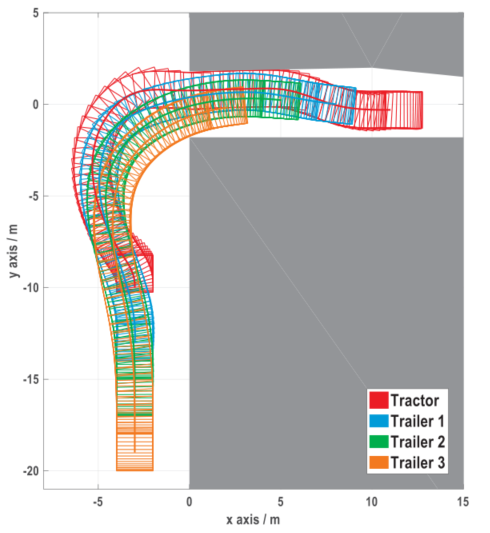
图6 案例3中优化的轨迹和对应的足迹(CPU时间为237.91秒，tf =21.68秒)


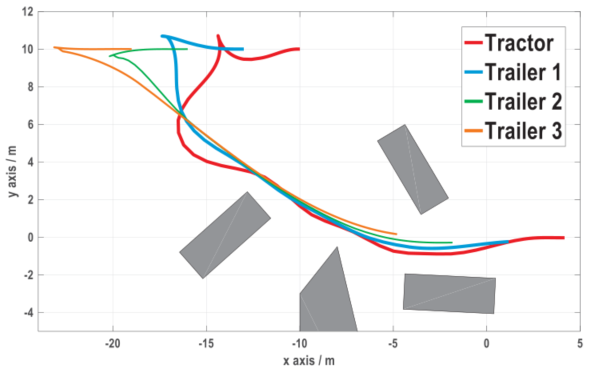
图7 案例2中牵引车/拖车的纯轨迹（从图5重新绘制）


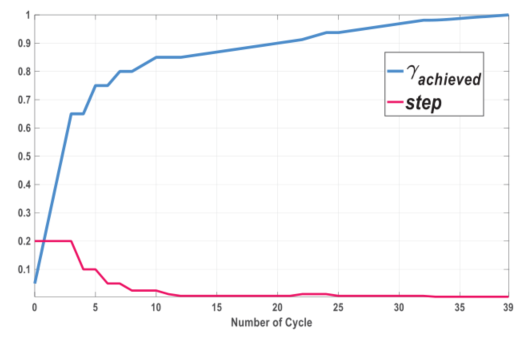
图8 算法1在案例1中的step和图片的演变过程

（二）与其他规划方法的对比

比较了算法1与[1]、[13]、[17]、[23]中的方法。[1]代表基本的数值优化，不需要初始化。通过简单地采用线性初始化，[1]中的求解器对于三种情况中的每一种都很快地收敛到不可行。这意味着初始化是有用的。[23]的方法是算法1的一个简单版本，它将step固定为指定的值。step设置过大，相邻子问题之间的间隙过大，失败是不可避免的;如果步长设置得小，与算法1的步长扩大策略相比，会浪费CPU时间。综上所述，从理论上讲，[23]的性能永远不会超过算法1。参考[17]根据代价函数值的演化，构建了类似的顺序自适应计算框架。这种策略在这里并不适用，因为成本函数值可能不是难度划分的好标准。[13]的方法是基于采样的方法。在一般的n拖车系统中，自由度远远小于状态剖面的维数，这使得将采样节点与运动学可行性联系起来变得困难。我们相信，当拖车数量增加时，增量搜索或基于采样的方法将逐渐变得效率低下。

（三）如何衍生在线解法？

采用非线性模型预测控制(NMPC)方法，在热启动的帮助下进行滚动优化，获得在线轨迹。以案例3为例，我们发现在后退水平中求解无限水平开环最优控制问题的平均CPU时间为1.29 s。对(8)进行简化可以进一步加快计算速度。我们可以预先离线准备典型轨迹，并利用它们作为在线NMPC框架中的参考解决方案。



参考文献