文章来源:广州汽车集团股份有限公司汽车工程研究院 0引言 近年来,国内外大力发展新能源汽车,永磁同步电机因具有功率密度高、体积小、重量轻、效率高等优点而得到广泛运用。 随着整车对动力性能的要求越来越高,电机的功率需求也越来越高,高热负荷下的温升
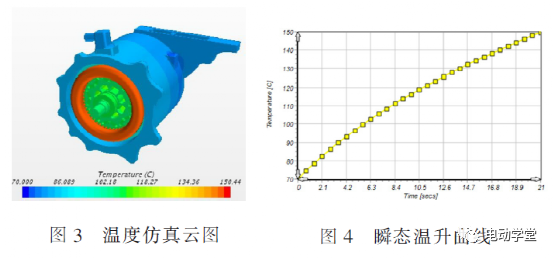
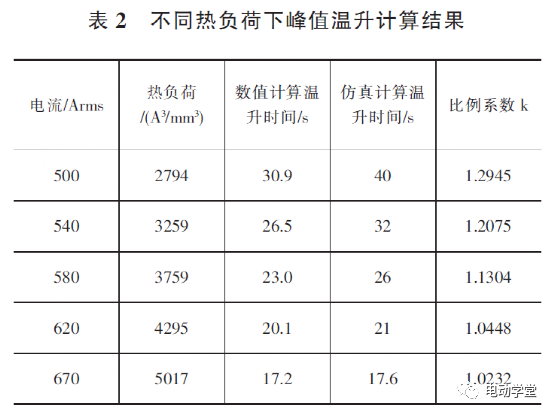
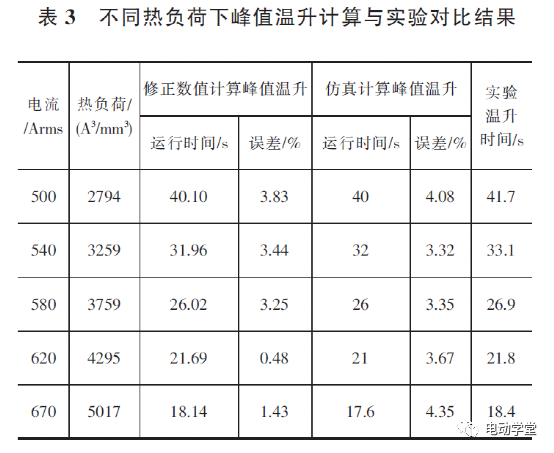
近年来,国内外大力发展新能源汽车,永磁同步电机因具有功率密度高、体积小、重量轻、效率高等优点而得到广泛运用。 随着整车对动力性能的要求越来越高,电机的功率需求也越来越高,高热负荷下的温升性能也成为挑战,准确、快速计算大功率电机峰值工况下温升(下文简称峰值温升)对电机设计研发意义重大。国内外学者对电机温升进行了大量研究, 主要方法有数值计算法、等效热网络法、有限元法等,以上研究大多聚焦于稳态工况,而对汽车用大功率 电机峰值工况运行的温升研究还相对较少。本文以一台200kW纯电动汽车用驱动电机为例,选取整车四驱百公里加速需求3s内的峰值扭矩运行工况,考虑整车存在重复多次加减速需求,电机峰值扭矩运行需求20s,采用数值计算和仿真分析分别求解得到电机峰值运行温升时间,并对数值计算模型进行修正,最后通过实验验证了求解模型的准确性。本文研究对象为一台峰值功率为 200kW的车用永磁同步电机,散热方式采用液冷,在420V电压、620Arms电流下,电机的基本参数如表1所示。电机峰值大电流、大扭矩运行工况,特别是高功率密度电机,其主要发热来自绕组铜耗和铁芯损耗, 且因绕组与铁芯之间存在导热系数低的绝缘纸、绝缘漆及空气等导致绕组热量短时无法散失而使绕组温度快速上升,而铁芯因与壳体接触而热量散失较快。假设电机绕组发出的热量全部被自身吸收,即有:式中: t为峰值运行时间,P Cu 为铜损,Cp为绕组比热容,M为绕组质量,T为电机某时刻温度,T0为电机绕组初始时刻温度。式中: m为绕组相数,I为相电流,R为相电阻,R0为 电机绕组初始相电阻,α 为Cu的电阻温度系数。考虑定子绕组阻值随温度变化, 实际的铜损计 算公式为:绕组通 620Arms大电流,计算得到电机起始70℃到150℃峰值运行时间为20.1s,满足目标要求。为校核数值计算模型的准确性, 本文同时通过有限元分析方法进行计算对比。根据传热学理论基础, 建立电机三维温度场数学模型,在直角坐标系下的求解域内三维非稳态导热微分方程和求解边界条件可表示如下:其中:λ x,λy,λz为物体在x,y,z方向的导热系数,λ为物体导热系数;qv为热源密度,ρ为物质密度;c为物质比热容,τ为时间项;S1,S2,S3为物体边界;q0为通过边界S2的热流密度;T'为物体待求解温度,T'0为边界S1的温度,Te为边界S3介质的温度,K;α为流体表面对流换热系数。电机水道内的冷却水状态为湍流, 其应满足如下三维控制方程:其中:ψ 为通用变量;u为流速;ξ为扩展系数;S ψ 为 源项。采 用有限元仿真软件对工作在峰值工况 ( 350Nm@620Arms)的电机进行温升仿真设置的边界 条件如下:(1)冷却水入口边界条件设为速度入口,流速为8L/min,入口水静态温度为70℃;(2)冷却水出口边界条件设为压力出口,出口压 力为 0Pa。搭建电机几何模型,包括壳体、水道、定子铁芯、绕组、转子铁芯、磁钢等,如图 1所示。在有限元软件 中进行网格剖分, 采用6面体网格,流体设置边界 层,如图 2所示。根据建立的热仿真模型, 在有限元软件中设置好热源、导热系数、求解步长等相关参数,得到峰值工况下电机运行达到150℃时的温度仿真云图如图3所示,绕组瞬态温升曲线如图4所示。仿真结果表明,在 620Arms电流下,电机内最高温度位于绕组端部且较大幅度高于其他部位,这是因为大电流工况绕组发热最大且冷却条件较差。电机绕组温度从70℃到150℃,时间为21s,与数值计算方法较接近。实际上,电机绕组发出的热量不可能全部被自身吸收, 有一部分被定子铁芯、电机内空气及冷却介质带走,因此需要对该计算模型进行修正。理论上,三相电流越大,电机热负荷越高,数值计算与实际的结果越接近,因此基于热负荷对计算模型进行修正。热负荷表征单位面积散发出去的热量, 其计算公式[7]见下文阐述。电机的线负荷A(沿着定子內圆单位长度内的电流)为:式中: m为相数,N为每相的绕线匝数,I为相电流,D 为定子内径。假设仿真计算结果是准确的, 为研究不同热负荷下数值计算准确性,分别采用两种方法计算500Arm~670Arms电流下的峰值温升(70℃~150℃) 时间见表 2。结果表明:热负荷越高,数值计算结果 与仿真计算结果越接近, 两者比值越接近于1,且620Arms以上误差较小。考虑数值计算方法的在不同热负荷下的通用性, 拟通过比例系数k(仿真计算结果/数值计算结果)进行修正,修正系数与热负荷的关系拟合曲线见图5。由图 5可知,修正系数与热负荷可拟合成二次 曲线,拟合关系式如下:其中: k 1 =5E-8,k 2 =0.0005,k 3 =2.3045。因此:修正的数值计算公式如下,系数 k 1 ,k 2 ,k 3 可根据不同电机类型做相应调整。为验证数值计算模型及仿真分析模型的准确性,搭建了电机温升实验台架,如图 6所示。电机通过工装与台架相连,电机高、低压线束与电机控制器相连后再连接电源柜,水道通70℃冷却水,水流量8L/min。通电测试,记录电机绕组温度从70℃至150℃的温升时间及对比误差见表3。实验结果表明,修正后的数值计算温升时间与实验误差在4%以内, 仿真计算温升时间与实验误差在 5%以内,两种计算方法具有一定的准确性。



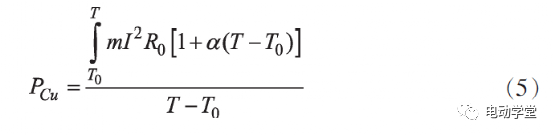
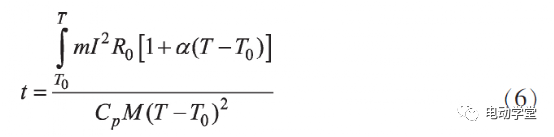
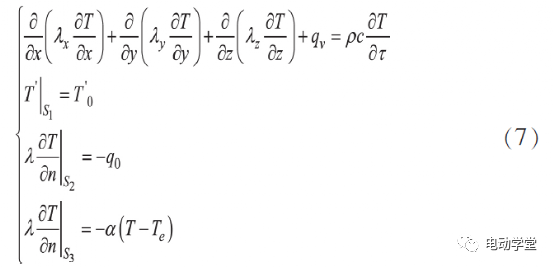




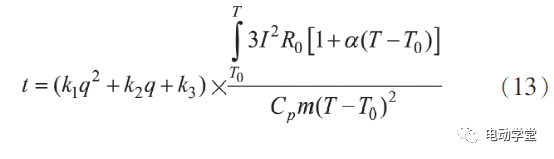





 广告
广告





























































