广告
一种应用于GPS反欺骗的基于MLE的RAIM改进方法
2021-02-28 17:33:23· 来源：轩辕实验室 作者：轩辕实验室
接收机自主完整性监控（RAIM）作为一种终端信号处理方法，最初旨在检测和排除故障。由于欺骗信号会导致错误的测量，因此可以将RAIM扩展到反欺骗领域，并且可以将欺骗信号视为故障信号。RAIM可以通过检测各种卫星的测量结果的一致性来检测故障并仅排除一个故障
接收机自主完整性监控（RAIM）作为一种终端信号处理方法，最初旨在检测和排除故障。由于欺骗信号会导致错误的测量，因此可以将RAIM扩展到反欺骗领域，并且可以将欺骗信号视为故障信号。RAIM可以通过检测各种卫星的测量结果的一致性来检测故障并仅排除一个故障。但是，通常同时存在多个欺骗信号。有学者提出了一种随机删除一些信号并测试其余信号的想法。作为该思想的扩展和实现，引入了随机遍历RAIM方法，该方法排除了部分信号，并对其余信号逐个执行RAIM测试，直到它们通过RAIM测试或测试所有信号组合为止。只要有四个以上的真实信号，就必须结合起来，所有其余信号都是真实信号，并且它们可以通过RAIM测试。因此，可以识别并排除多个欺骗信号。但是，它需要测试接收信号的所有可能组合。例如，假设有14个信号，其中包括8个真实信号和6个欺骗信号，则最佳情况下需要的RAIM测试数量为1472，最坏情况下为3468。如果有更多的信号，则数量会更多。因此，复杂度很高，严重限制了实时接收机中的应用。本文提出了一种用于反欺骗的一维遍历MLE-RAIM（TMRAIM）方法，基于最大似然估计（MLE）理论来降低遍历RAIM方法的复杂性。
本文来自本实验室李王睿的学习笔记。
本文来自本实验室李王睿的学习笔记。
为了在低复杂度的实时接收机上检测和排除多种欺骗信号，本文提出了TMRAIM方法。首先，详细介绍了RAIM的数学模型。然后，在知道了欺骗信号的数量的情况下，通过MLE推导推论如何仅一次找到所有欺骗信号。最后介绍了TMRAIM方法，该方法可以在一维遍历的情况下应用于多欺骗环境。
RAIM的数学模型
为了理解RAIM的特性，其数学模型介绍如下。在单个星座图中，未知数是一个二维矢量，包括时钟偏差和位置。当有M（M> 4）个测量值时，测量方程可表示为：
其中z是一个M维向量，表示伪距残差；G是从解空间到测量空间的M×4几何矩阵。x是一个二维矢量，包括时钟偏差和位置；n是一个M维向量，表示测量误差，每个元素服从标准差等于σ的独立零均值高斯分布；b是没有补偿的测量偏差（故障）的多维向量。在欺骗下，b代表欺骗偏差，其分量（1
基于最小二乘法，可以得到的估计量
其等效于将M维的向量z投影到四维的解空间，这会导致信息丢失。因此，可以构造奇偶矩阵来恢复丢失的信息，该信息是M-4维的奇偶矢量。结果如下：
其中是奇偶矢量，P是（M-4）×M维的奇偶矩阵。而奇偶矢量可以由如下公式所求：
因此，可以获得奇偶矢量的数学期望和方差：
其中σ是（1≤i≤M）的方差，并且是n的第i个分量。
因此，测得的伪距残差矢量w可以表示为
最后，获得误差平方和SSE：
可以证明，当b = 0（无故障且无欺骗信号）时，SSE符合中心卡方分布；当b≠0时，SSE符合非中心卡方分布。卡方分布的自由度为。由于SSE的概率分布是已知的，因此可以通过预设的虚假警报概率来确定检测阈值。例如，如果误报率为1‰，M等于10，则等于22.4577。
在五个以上的卫星信号且其中只有一个卫星故障的情况下，基于条件概率的最大值，常规RAIM也可以用于故障排除。具体描述如下
故障检测与排除（FDE）是指被标识为故障卫星的相应卫星的数量。是向量w的第i个分量，而是矩阵S对角线上的第i个元素。
利用MLE实现排除欺骗信号
传统的RAIM只能排除一个欺骗信号。基于MLE理论，可以推断出在假设k个欺骗信号的情况下如何排除所有欺骗信号。奇偶矢量的条件概率分布如下
根据MLE理论，使最大的是b的估计量。通过扩展等同于：
其中b代表欺骗性偏差，其分量（1≤i≤M）代表相应信号的欺骗性偏差。如果第ith个信号是真实信号，则=0。因此，当存在k个欺骗信号时，向量b中仅对应的k个元素不为零。此外，为了获得
，我们可以求导得到极值点
其中是由向量b中的k个非零元素组成的k维向量；是由向量w中相应的k个元素组成的k维向量；是通过交叉矩阵S中相应的k行和k列而得到的k×k矩阵。
令上式等于0，可以得到与极点相对应的，并进一步得到：
最后，可以通过找到的最大值来获得对应的k个欺骗信号数FDEs：
如果从M个元素中提取k个元素，则总共有个组合。因此，我们可以获得个的值。可以通过比较所有值来获得最大值。根据MLE理论，对应于最大值的信号是欺骗信号。因此，在假设有k个欺骗信号的情况下，与需要大约次的随机遍历RAIM方法相比，通过执行一次常规RAIM可以找到对应的欺骗信号, 计算复杂度大大降低。
提出的TMRAIM方法
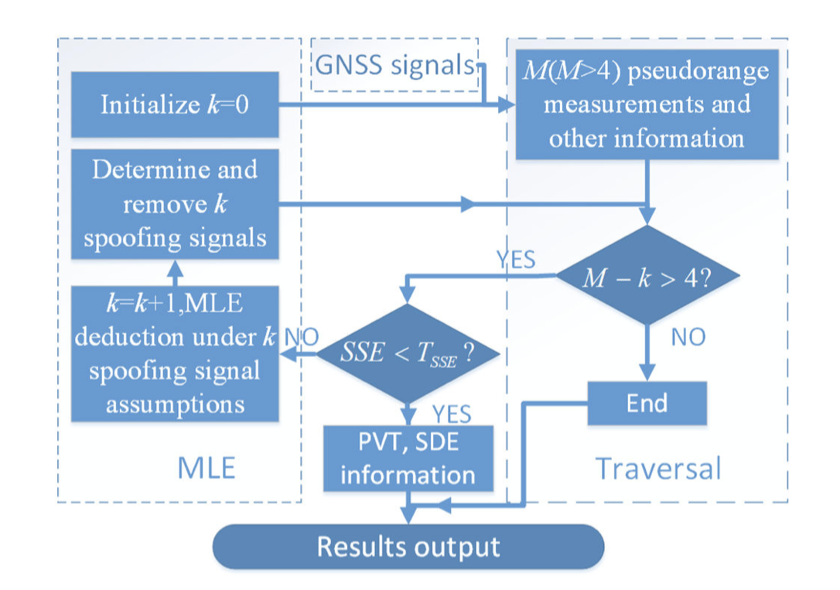
通过基于MLE的推论，扩展了传统RAIM从只能排除一个欺骗信号到排除多个欺骗信号，但前提条件是事先知道欺骗信号的数量，这在实际欺骗环境中是很难做到的。常规RAIM的完整性可用于判断所有剩余信号是否均为真实信号。因此，我们可以首先假设欺骗信号的数量为零，然后依次增加欺骗信号的数量。每次排除之后都要进行RAIM测试，以确保排除所有欺骗信号。本文提出了一种实用的反欺骗方法TMRAIM，其流程图如下图所示。
当接收到的信号数大于四个时，就将启动该方法。具体步骤如下：
初始化k=0 根据伪距，卫星坐标和预设的误报率，计算SSE和 执行RAIM测试，比较SSE和 如果RAIM没有报错，输出正确的位置、速度、时间 如果RAIM报错了，使k=k+1；然后在有K个欺骗信号的假设下执行上述MLE推论。 找到使最大的k个欺骗信号并移除这些信号；然后回到步骤2 当M-K小于等于4或RAIM测试没有报错时，循环终止
可以将TMRAIM方法添加到接收器的定位解决方案模块中，以在每个定位方案中实现SDE。当接收到的信号大于四个时，将检测到欺骗信号，而当接收到的真实信号至少为五个时，将排除欺骗信号。仅遍历一维的欺骗信号。因此，TMRAIM方法具有较低的时间复杂度，可以应用于实时接收器中以排除多个欺骗信号。
测试
为了验证TMRAIM方法的实用性，进行了两个现场实验。为了模拟手机上的应用，首先在软件接收器上实现它，以通过软件更新的方式处理来自手机的原始数据。构造并测试了具有三个欺骗信号的场景。此外，为确保至少接收到五个真实信号，设计并实现了一种具有多峰值采集能力的新接收器。产生具有四个欺骗信号的中间欺骗攻击，并显示相关的实验结果。实验中RAIM测试的误报率设置为1‰。
为了验证该方法的实用性，本文在软件接收器上实现了该方法，以处理来自手机的原始数据。此外，在屋顶上建造了一个自洽的接收器/欺骗器。GPS欺骗模块构建在FPGA上，以通过GPS接收器，上变频器，功率放大器和发射天线来接收和转发GPS信号。作为GPS接收器的手机将同时接收到真实的欺骗信号。由Google提供的GNSS观测提取工具GnssLogger App已安装在手机上。它可用于从GNSS信号中提取实时信息，例如卫星位置和伪距观测值。然后，相关信息被存储以在软件接收器上运行。
在实验中，GNSS发射器接收GPS信号，并以3μm的延迟重传其中的三个。转发信号的对应PRN分别为7、8和16。除了接收三个转发信号之外，接收器还接收七个PRN为9、11、18、23、27、28和30的真实信号。遍历这三个欺骗信号假设时，存在组合。
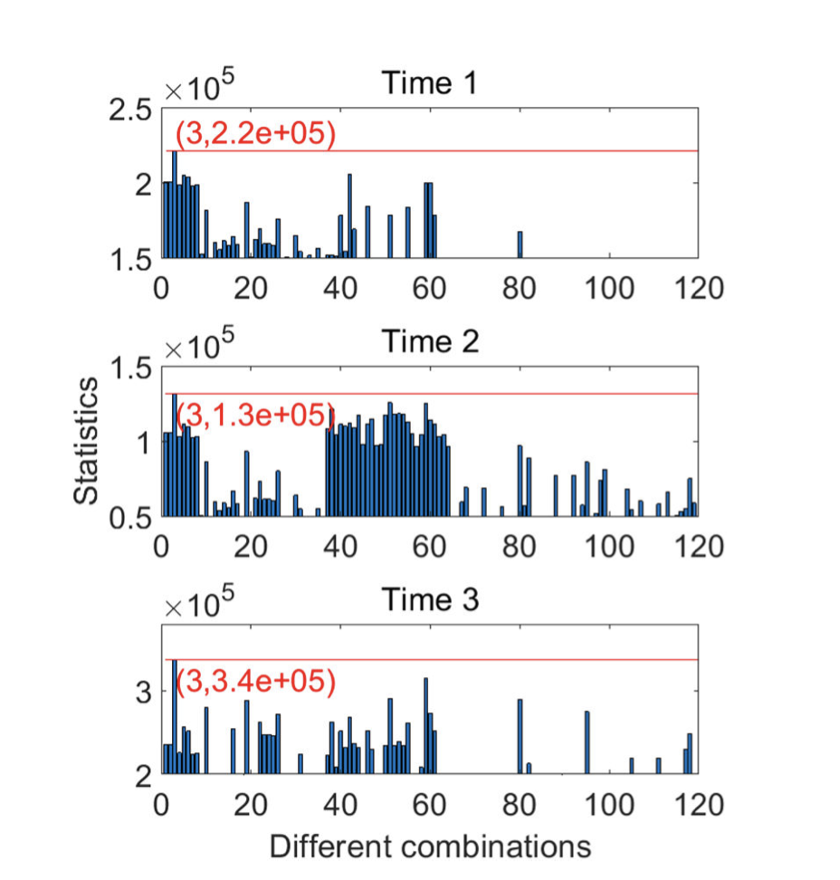
下图展示出了在三个不同时间对应于不同组合的识别统计。
可以通过TMRAIM方法找到与的最大值相对应的组合。在图中，红色括号中的坐标表示与120个统计量中的最大值相对应的坐标，其统计量在三个不同时间处最大的组合为组合3。因此，TMRAIM方法有效地找到了所有欺骗信号。
参考文献：
Li, Jianfeng; Li, Hong; Lu, Mingquan: 'One-dimensional traversal receiver autonomous integrity monitoring method based on maximum likelihood estimation for GNSS anti-spoofing applications',
Sagar Dasgupta, Mizanur Rahman, Mhafuzul Islam, Mashrur Chowdhury: 'PREDICTION-baseD GNSS SPOOFING ATTACK DETECTION FOR AUTonOMOUS VEHICLES'
广告
广告
编辑推荐
最新资讯
-
厂商要多努力，才能让用户听起来毫不费力？
2024-11-22 17:10
-
TOP30！海克斯康入选2024福布斯中国数字科
2024-11-22 15:25
-
揭秘国产装备制造厂商的成功秘籍：好耐电子
2024-11-22 15:24
-
一文详解安全分析方法STPA：以自动紧急制动
2024-11-22 15:20
-
选对涉氢压力表：守护涉氢场所安全的关键一
2024-11-22 15:19
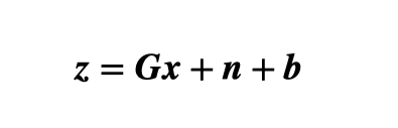
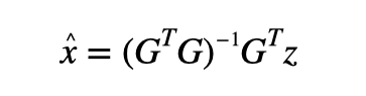
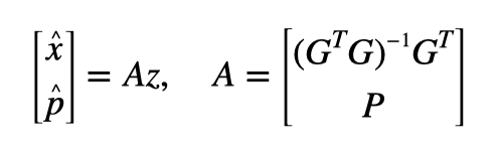
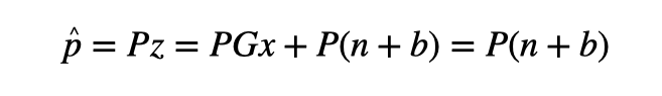
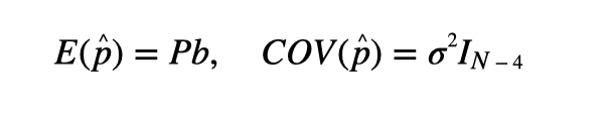
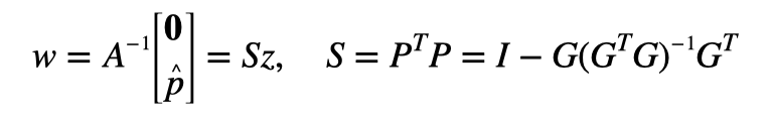
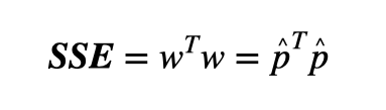
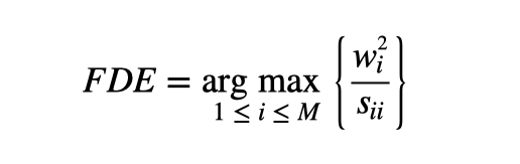
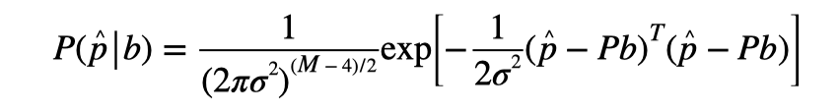
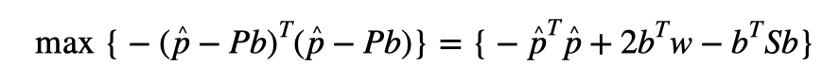
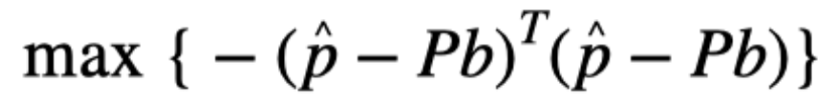
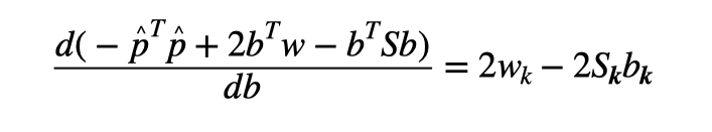
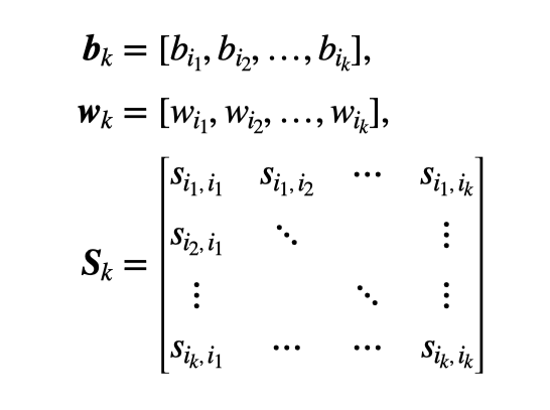
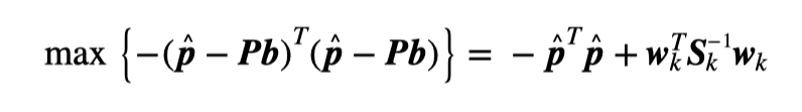
广告
广告
