采用KIVA-3V 程序开展柴油/天然气双燃料发动机的计算研究。其中湍流模型采用的是适用于变密度缸内流动的RNG k-ε模型;液滴破碎过程采用KH-RT模型,将湍流火焰速度封闭模型(TFSC)与PaSR燃烧模型耦合建立复合燃烧模型模拟双燃料发动机燃烧过程;碳烟生成及氧化过程采用瑞典Golovitchev教授提出的碳烟模型进行预测,碰壁模型采用了Han 和Reitz 模型。其中,湍流火焰传播模型(turbulent flame speed closure,TFSC)采用了Bray-Moss 方法,并通过燃烧进程变量来表征燃烧过程。湍流火焰传播方程为
式中:ρ为混合气的费尔平均密度;ρu为未燃烧混合气的密度;c为燃烧进程变量,变化范围为0~1,其中未燃区为0,已燃区为1;τf为燃料反应特征时间;St为湍流火焰传播速度,取决于层流火焰传播速度和流动湍流的特性。湍流火焰传播速度的计算方法为
式中:Sl为层流火焰传播速度;δl为火焰厚度。
双燃料发动机的复合燃烧模型用质量守恒方程进行描述为
式中:ρc1m为PaSR燃烧模型的化学反应项;ρc2m为TFSC 燃烧模型的化学反应项;u为速度向量; τc1为PaSR 燃烧模型特征时间;τc2为TFSC燃烧模型特征时间;cm为反应物浓度。
双燃料燃烧模型的总体特征时间为
层流火焰传播速率由参考点的层流火焰传播速率通过拟合得到,如公式(6)所示
式中:S10为参考点层流火焰速度;p和T为未燃烧混合物的压力和温度;p0和T0为参考点的压力和温度,参考点p0=5MPa、T0=450 K。式(6)与STAR-CD 程序中计算层流火焰传播速度的方法相同。
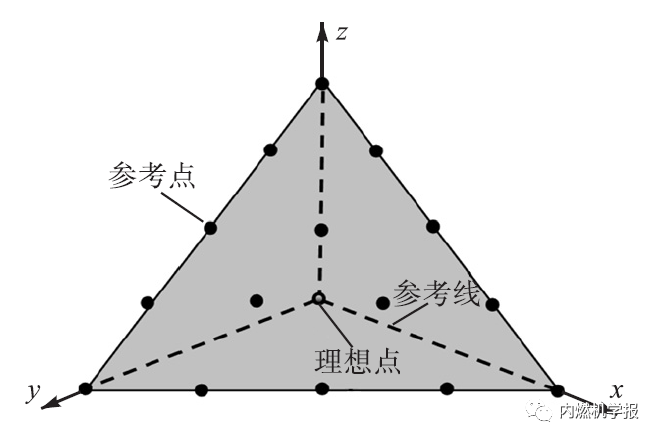
目前绝大多数遗传算法的优化研究均基于Deb等提出的非支配排序遗传算法(NSGA-2)。NSGA-2通过采用快速非支配的排序算法,降低了计算非支配排序的复杂度,同时引入了精英策略,扩大了采样空间。为了更好地求解多目标优化问题,Deb等通过改进NSGA-2 提出了一种新的NSGA-3算法。在NSGA-3中,使用一组预定义的参考点(线)来确保最优解分布的均匀性。所选择的参考点可以通过公式预定义或由用户自主设置得到。距离参考点(线)的距离最小个体将被选择为优选解,如图1 所示。在这种算法下,所选择的最优解会广泛分布于Pareto最优前沿面,Pareto解又称非支配解或不受支配解:在进行多个目标优化时,由于目标之间存在trade-off 关系,在改进任何目标函数的同时,必然会削弱至少一个其他目标函数的解,称为非支配解或Pareto解。一组目标函数最优解的集合称为Pareto最优集,最优集在空间上形成的曲面称为Pareto前沿面。
图1 NSGA-3参数选择机制
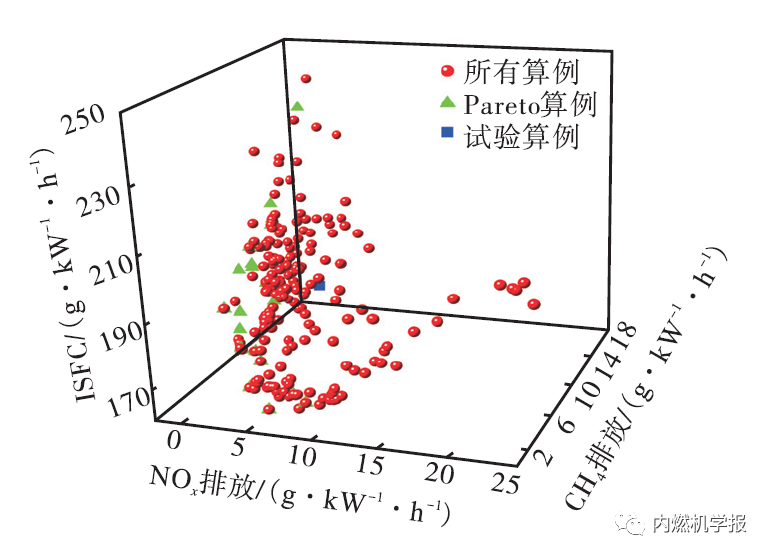
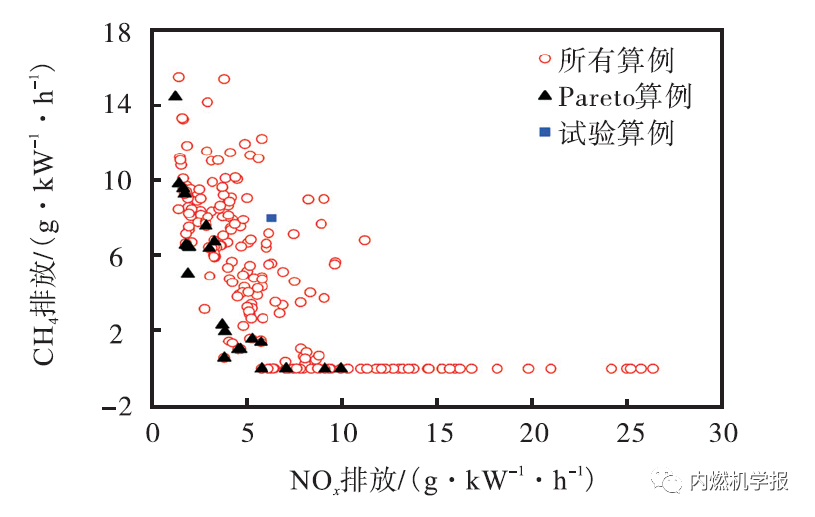
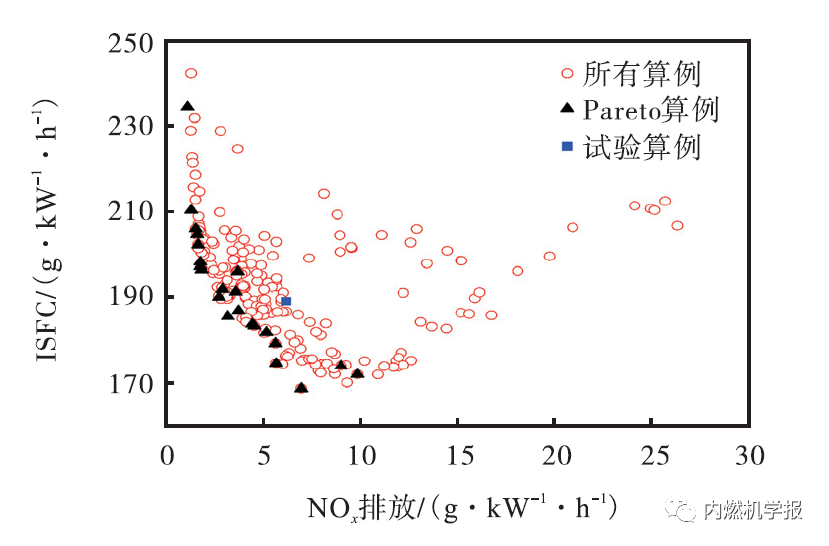
由于双燃料发动机的碳烟排放较低,而甲烷及NOx排放较高,因而将CH4排放、NOx 排放和指示燃料消耗率(ISFC)3个参数作为优化目标。通过设置最大压力升高率(dp/dφ)max <2 MPa/(°)CA、缸内峰值压pmax ≤20 MPa 和可接受的最大指示燃油消耗ISFC≤250 g/(kW·h)作为约束条件,从而排除由于参数匹配不当导致的爆震、机械负荷过高或预混天然气未能完全燃烧等现象,确保发动机运行在合理的工况内。其中,ISFC 为折合燃料消耗率,由式(7)和式(8)计算获得。
燃料消耗量mdual为
燃料消耗率bdual
式中:mdual、mdiesel和mCNG分别为双燃料、柴油及天然气的消耗量;Hu,CNG、Hu,diesel分别为天然气和柴油的低热值,Hu,CNG/Hu,diesel =1.15。
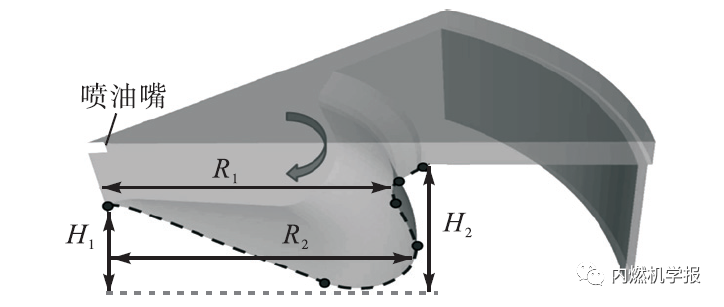
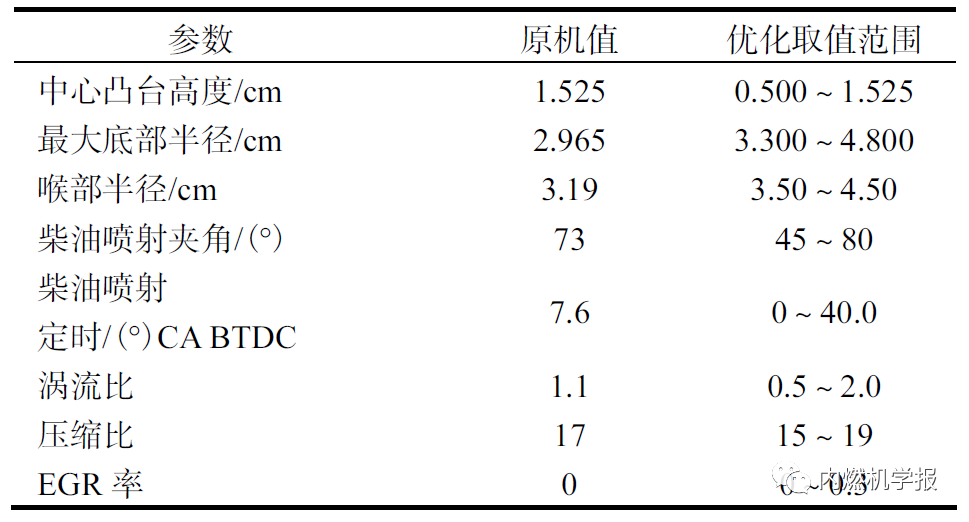
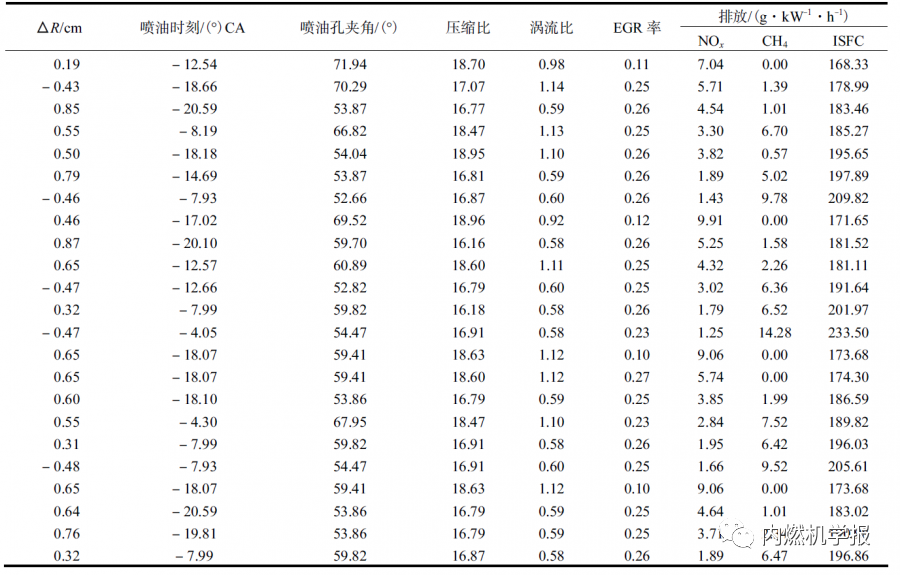
所优化的参数包括两个引燃柴油喷射参数为喷油定时和喷油夹角;4个燃烧室结构参数为中心凸台高度H1、喉部半径R1、最大底部半径R2 和压缩比;两个运行参数为涡流比和EGR率,如图2 所示。表1为原机参数和优化过程中8个参数的取值范围。
图2 燃烧室形状参数定义及控制点
表1 优化参数及其变化范围
主要研究柴油/天然气发动机的缸内燃烧过程,不考虑进/排气过程的影响,因而计算过程只考虑从进气门关闭到排气门打开期间燃烧室内进行的压缩、燃油喷射、油气混合及燃烧过程,计算区间为从进气门关闭角(146 °CA BTDC)至排气门开启角(120 °CA ATDC)。
所采用发动机的燃烧室为中心对称结构,且喷油器的位置在燃烧室中心处,因而为了提高计算效率,选取整个燃烧室的七分之一进行计算。燃烧室的网格通过自行开发的燃烧室网格自动生成软件进行自动划分,该方法为通过选取燃烧室上的几个特征点来定义燃烧室的结构,燃烧室的外部轮廓线由连接这些特征点之间的曲线进行拼接得到,图2为燃烧室几何形状的参数定义和控制点的选择。在计算过程中无需人为设置燃烧室网格,优化过程能够自动完成。
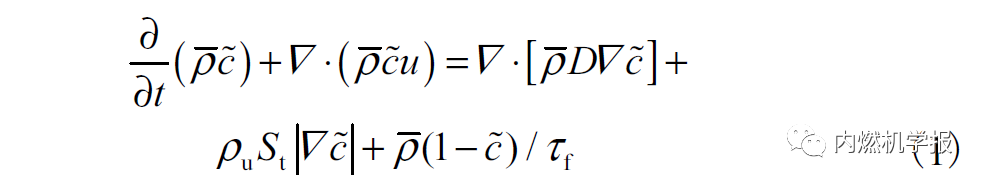
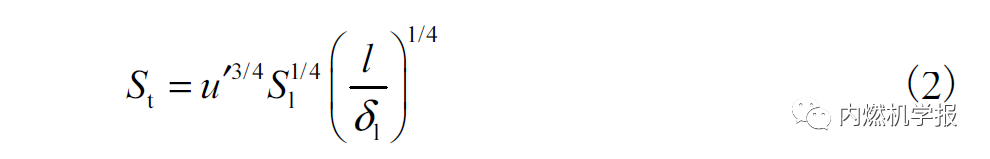
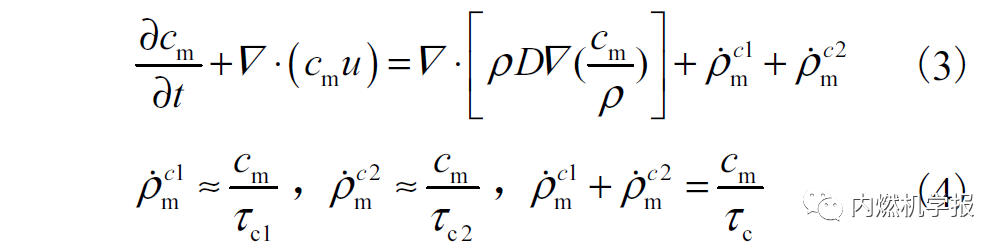

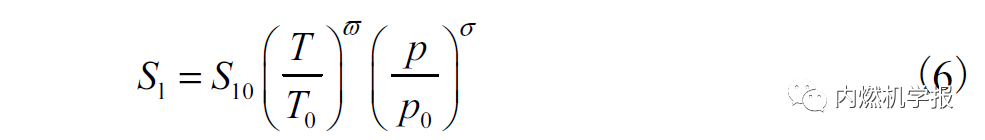







 广告
广告





























































