编者按:路口是车路协同的重要应用场景。对于交通灯控制的路口,路端信号灯时序的优化与对应车端车辆轨迹的规划是改善路口拥堵,提高通行效率的有效措施。由于信号灯时序与车辆轨迹的协同规划能够最大程度发挥路口通行能力,应对各类动态交通需求,已得到研究的广泛关注。但协同优化问题的难点在于问题复杂,建模求解难度较大,难以在计算效率与解质量间取得较好平衡。而本文将信号时序和轨迹协同优化问题表示为一个非线性的混合整数优化问题,同时通过线性化非线性约束等措施重构简化问题,再根据车道信号需单独控制的特点将路口级问题分解为多个车道级子问题,提高了算法的求解质量与求解效率。
本文译自:
Traffic Signal Timing and Trajectory Optimization in a Mixed Autonomy Traffic Stream
文章来源:
February 2021. IEEE Transactions on Intelligent Transportation Systems PP(99):1-14
作者:
Mehrdad Tajalli and Ali Hajbabaie
原文链接:
https://ieeexplore.ieee.org/document/9357468
摘要:这项研究介绍了一种针对自动驾驶车辆(CAV)与人类驾驶车辆(HV)混合交通流的路口交通信号配时和车辆轨迹优化协同方法。本文将信号时序和轨迹协同控制问题表示为一个非线性的混合整数优化问题,但其具有较高的计算复杂度。因此,本文通过以下两措施对计算效率和解质量进行平衡。(a)线性化非线性约束并借助混合整数规划解的紧凸壳重构问题 (b)将路口级问题分解为几个车道级问题。因此,得到了一种可同时优化车道级CAV轨迹以及对应车道信号时序参数的新控制器。本方法可为不同需求水平的复杂路口得到较小对偶间隙的近似最优解。案例研究结果表明,本文提出的方法可有效地找到对偶间隙最多为0.1%的解。在将本文方法与现有信号定时和轨迹控制方法比较后发现,不同情况下的平均行驶时间减少了13%至41%,燃油消耗减少了1%至31%。
关键词:交通信号配时,轨迹优化,智能网联汽车、拉格朗日松弛
研究表明,优化智能网联车辆(CAV)轨迹和路口交通信号灯时序具有改善交通的巨大潜力[1]-[5]。CAV轨迹与信号定时的协同优化有助于更准确地规划车辆的路口到达时间,从而更有效地利用路口绿灯时间,减少车辆的路口停车次数、燃料消耗和行程延误。但是,交通信号控制器与将到达车辆间的协作需要的通信和计算能力是巨大的[6],而信号控制器难以处理所有所需计算。此前已有相关研究在以下场景下证明了信号时序和轨迹优化的有效性。(a)简单结构路口(例如,单向街道[2],[7]或直道[8]),(b) 低交通流量路口[2],[7]-[9],(c)基于简化或限制性假设路口(例如,以一阶流量模型计算CAV轨迹或部分CAV轨迹)。而逼近法和启发式算法被用于求解复杂场景,但其是以牺牲解质量为代价[11],[12]。
本文提出了一种针对信号灯控制路口的CAV轨迹和信号时序协同优化方法,该方法可较好地平衡计算效率和解质量。如图1所示,该方法专为CAV和HV的混合交通流而设计,其中CAV的移动受到集中控制,并通过路口处的V2I设备进行通信。该方法需获取路口附近所有车辆(CAV和HV)的初始位置和速度,而使用汽车跟随模型在规划的前瞻时间段内预测HV的对应位置,但HV的运动未被优化。本文假设所有车辆都是网联车辆(只是为了收集车辆位置和速度),或者路口配备了可提供车辆位置和速度的传感器(例如雷达或摄像机)。注意,如果HV不向信号控制器传输信号,只要有传感器可收集到所需数据,本文的算法就可正常工作。本文将该协同优化问题转化为非线性的混合整数规划问题,旨在减少路口车辆的总行驶时间和车速变化。其中决策变量为CAV的加速度和信号时序参数。本文使用了Helly[13]中的线性跟车模型考虑HV和CAV间的相互作用,同时通过合并线性模型中信号时序参数的方式体现模型对交通信号的响应。信号时序参数通过无周期相位的规划进行优化,不仅满足了黄灯时间的约束,还满足了最小最大绿灯时间的约束。
图1 与CAV和HV交互的信号控制器
交通信号配时和轨迹优化(STTO)问题十分复杂,尤其车流中存在人类驾驶车辆时,因此需要开发计算效率较高的算法以搜寻近似最优解。此前的研究已表明求解算法需在计算效率和解的最优性间进行权衡取舍。本文引入了一种新的求解方法,该方法使用拉格朗日松弛法将路口级信号时序和轨迹优化问题分解为几个车道级的优化子问题,从而降低STTO问题复杂度,从而在路口的每个车道上对信号时序参数和CAV轨迹进行优化。结果,STTO可拓展到高需求水平的复杂路口情况。此外,本文提出了一种基于路口冲突图的最大团集的问题重构方法,以收紧混合整数可行区域凸壳,从而提高拉格朗日松弛方法的收敛性,减小最优间隙。通过路口处所有控制器协同可搜寻近似最优的路口信号配时参数和CAV轨迹。此外,本文还额外构造了一个求解信号时序规划的简单优化问题,保证在没有上述限制性假设情况下,算法可得到高质量可行解。
这项研究协同优化了所有CAV的轨迹和信号配时参数。假定路侧设备通过雷达单元,视频检测或通信连接获得了人类驾驶车辆的初始位置和速度。我们将L定义为十字路口所有车道的集合,将I定义为十字路口邻域内所有车辆的集合。此外,Il,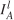 和
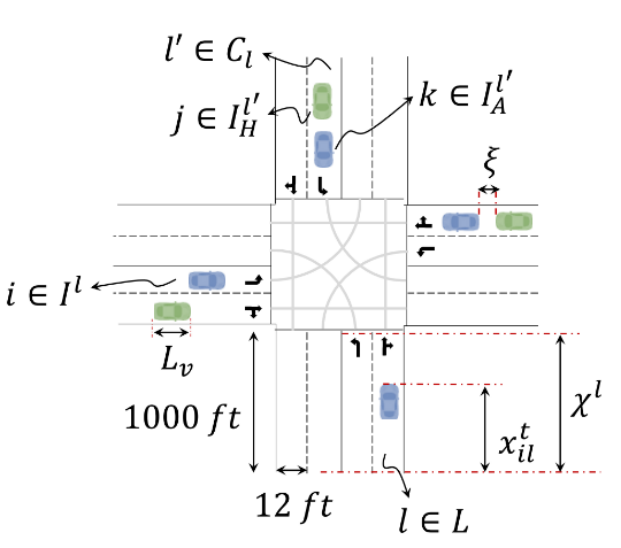
和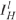 分别表示车道l∈L上所有车辆,CAV和HV的集合。我们将Cl定义为与车道l∈L冲突的所有车道集合。图2显示了孤立路口中定义的集合。我们将Ts和Tt分别定义为信号时序和轨迹优化的时间步长集合。注意,车辆轨迹和信号配时更新的时间步长(分别为Ts和Tt)不同。车辆轨迹比信号配时参数更新频率更高,以考虑驾驶员行为的不确定性,并获取预测车辆轨迹和实际车辆轨迹间的偏差。等式(1)表示了两时间步长间关系。运算符
分别表示车道l∈L上所有车辆,CAV和HV的集合。我们将Cl定义为与车道l∈L冲突的所有车道集合。图2显示了孤立路口中定义的集合。我们将Ts和Tt分别定义为信号时序和轨迹优化的时间步长集合。注意,车辆轨迹和信号配时更新的时间步长(分别为Ts和Tt)不同。车辆轨迹比信号配时参数更新频率更高,以考虑驾驶员行为的不确定性,并获取预测车辆轨迹和实际车辆轨迹间的偏差。等式(1)表示了两时间步长间关系。运算符 表示将相应参数四舍五入。信号配时变量(包括时间p∈Ts时车道l∈L下的绿灯时间
表示将相应参数四舍五入。信号配时变量(包括时间p∈Ts时车道l∈L下的绿灯时间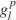 ,黄灯时间
,黄灯时间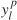 )将基于将近路口车辆i∈Il的位置
)将基于将近路口车辆i∈Il的位置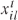 速度信息
速度信息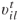 进行优化。时间t∈Tt时车辆i∈
进行优化。时间t∈Tt时车辆i∈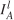 的加速度
的加速度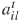 也是CAV运动规划的控制参数。表I列出了问题描述中的变量,集合和参数定义。
STTO的目标函数表示为(2)中的两项。第一项最大化各车辆 i∈Il距车道l∈L起点距离(参见图2)[29],[30]。车道l∈L上车辆i∈Il的权重因子ωil对目标函数第一项加权,以避免连续处理高需求交通流量,并防止车辆在路口次要方向上排队。本文将该权重值设为各车进入路口后的延迟时间(即自由流行驶时间减去实际行驶时间)。因此,较高的历史延迟的车道上车辆将拥有更高的通行优先级。请注意,权重参数在规划前瞻时间内为定值。目标函数的第二项通过最大程度地减小两连续时间步长间的各CAV速度差以平滑CAV运动。所有车辆的速度和位置都是根据基本运动方程进行更新,如约束(3)和(4)。1)车辆跟车约束:HV的位置和速度的估计是信号时序参数和CAV轨迹协同优化所必需的。本文基于跟车模型预测HV未来轨迹。本文考虑了由Helly(1959)开发的线性跟车模型,该跟车模型被用于对自适应和协作式巡航系统建模[31],[32]。同时Helly的跟车模型与现实交通数据的匹配性在Panwai和Dia(2005)中体现了。尽管人类驾驶行为是随机的,但具有确定性的跟车模型在本方法是有效的。其原因是滚动时域控制方法每0.5秒获取车辆在交通网的初始位置,这将在方法部分中进行说明。在该跟车模型中,车辆对相对前车的相对速度和与距离做出响应,其加速度由(5)计算。参数α1和α2是固定正值,其取值范围参考[34],[35]中的[0.17,1.3]和[0.25α1,0.5α1]。等式(5)中的第一项考虑了前后车的相对速度。第二项考虑了连续车辆的相对距离。本文改进了跟车模型以考虑交通信号使车辆在接近红灯时减速的行为。该交通信号被考虑为一虚拟车辆,其可在停车线处的速度为零停车(对于红色信号)或在路口处以最大速度最大速度行驶(对于绿色信号)。等式(6)显示了车辆在接近停止线时如何更新其加速度。请注意,当交通信号为红灯时,
也是CAV运动规划的控制参数。表I列出了问题描述中的变量,集合和参数定义。
STTO的目标函数表示为(2)中的两项。第一项最大化各车辆 i∈Il距车道l∈L起点距离(参见图2)[29],[30]。车道l∈L上车辆i∈Il的权重因子ωil对目标函数第一项加权,以避免连续处理高需求交通流量,并防止车辆在路口次要方向上排队。本文将该权重值设为各车进入路口后的延迟时间(即自由流行驶时间减去实际行驶时间)。因此,较高的历史延迟的车道上车辆将拥有更高的通行优先级。请注意,权重参数在规划前瞻时间内为定值。目标函数的第二项通过最大程度地减小两连续时间步长间的各CAV速度差以平滑CAV运动。所有车辆的速度和位置都是根据基本运动方程进行更新,如约束(3)和(4)。1)车辆跟车约束:HV的位置和速度的估计是信号时序参数和CAV轨迹协同优化所必需的。本文基于跟车模型预测HV未来轨迹。本文考虑了由Helly(1959)开发的线性跟车模型,该跟车模型被用于对自适应和协作式巡航系统建模[31],[32]。同时Helly的跟车模型与现实交通数据的匹配性在Panwai和Dia(2005)中体现了。尽管人类驾驶行为是随机的,但具有确定性的跟车模型在本方法是有效的。其原因是滚动时域控制方法每0.5秒获取车辆在交通网的初始位置,这将在方法部分中进行说明。在该跟车模型中,车辆对相对前车的相对速度和与距离做出响应,其加速度由(5)计算。参数α1和α2是固定正值,其取值范围参考[34],[35]中的[0.17,1.3]和[0.25α1,0.5α1]。等式(5)中的第一项考虑了前后车的相对速度。第二项考虑了连续车辆的相对距离。本文改进了跟车模型以考虑交通信号使车辆在接近红灯时减速的行为。该交通信号被考虑为一虚拟车辆,其可在停车线处的速度为零停车(对于红色信号)或在路口处以最大速度最大速度行驶(对于绿色信号)。等式(6)显示了车辆在接近停止线时如何更新其加速度。请注意,当交通信号为红灯时,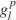 =0,虚拟的停止车辆位于路口停止线χl处,车辆与路口停止线的安全距离为ξ。当绿灯时候,前一虚拟车辆位置将被设为与后车较远的位置,并且车辆到路口停车线的安全距离将减为零。此外,应注意的是仅当车辆位置路口停车线前时,才需要考虑车辆与交通信号灯间的交互关系。在CAV通过路口后,式(6)失效。绿灯时,等式(6)的第二项中将信号时序变量
=0,虚拟的停止车辆位于路口停止线χl处,车辆与路口停止线的安全距离为ξ。当绿灯时候,前一虚拟车辆位置将被设为与后车较远的位置,并且车辆到路口停车线的安全距离将减为零。此外,应注意的是仅当车辆位置路口停车线前时,才需要考虑车辆与交通信号灯间的交互关系。在CAV通过路口后,式(6)失效。绿灯时,等式(6)的第二项中将信号时序变量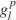 乘以较大系数M,将虚拟汽车移动到与后车较远的位置。这样后车将不再对其作出反应。式(6)二元变量
乘以较大系数M,将虚拟汽车移动到与后车较远的位置。这样后车将不再对其作出反应。式(6)二元变量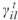 是为了解除车辆通过停止线后与信号灯的连接。方程(5)和(6)表示的线性跟车模型没有限制加速度和速度取值。因此,我们根据max-min函数建立了车辆跟车模型,如方程式(8)所示。此公式是拟议跟车模型的完整形式,该模型描述了车辆在自由交通流下跟随其他处于静止和非静止状态车辆,和接近慢速或停止车辆以及红色信号等情况。2) CAV运动约束:目标函数(2)是为了平滑CAV轨迹以防止车辆在路口频繁停车。约束(9)确保CAV与前车的安全距离。两连续车辆间的距离是所需的安全距离ξ,平均车辆长度Lv和后车反应时间内通过距离的函数。其中τA表示CAV反应时间。当信号不为绿时,约束(10)用于防止CAV进入路口中间区域。安全距离是车辆在当前时刻t∈Tt处以当前速度在一时间步长中可行驶的最大距离的函数。该约束在绿灯或车辆已通过停止线时失效。因此信号时序变量需乘上一个较大的数(M)以保证无论信号为绿灯还是车辆已通过了停止线时,都能满足约束(10)。约束(11)和(12)分别将CAV的加速度和速度的范围进行限制。3)信号时序约束:本文为防止车辆间因相冲突航向而发生碰撞,考虑了以下几个约束。当时间步长p∈Ts下车道l∈L交通信号为绿或黄时,信号时序变量均为1。否则,同时取值零,反映此时信号为红。约束条件(13)可确保在时间步长为p∈Ts时没有一对相互冲突的航向能同时收到非红交通信号。另外,约束(13)也可防止车道信号同时变绿或黄。约束(14)确保车道的绿灯时间小于或等于设定的最大绿灯时间
是为了解除车辆通过停止线后与信号灯的连接。方程(5)和(6)表示的线性跟车模型没有限制加速度和速度取值。因此,我们根据max-min函数建立了车辆跟车模型,如方程式(8)所示。此公式是拟议跟车模型的完整形式,该模型描述了车辆在自由交通流下跟随其他处于静止和非静止状态车辆,和接近慢速或停止车辆以及红色信号等情况。2) CAV运动约束:目标函数(2)是为了平滑CAV轨迹以防止车辆在路口频繁停车。约束(9)确保CAV与前车的安全距离。两连续车辆间的距离是所需的安全距离ξ,平均车辆长度Lv和后车反应时间内通过距离的函数。其中τA表示CAV反应时间。当信号不为绿时,约束(10)用于防止CAV进入路口中间区域。安全距离是车辆在当前时刻t∈Tt处以当前速度在一时间步长中可行驶的最大距离的函数。该约束在绿灯或车辆已通过停止线时失效。因此信号时序变量需乘上一个较大的数(M)以保证无论信号为绿灯还是车辆已通过了停止线时,都能满足约束(10)。约束(11)和(12)分别将CAV的加速度和速度的范围进行限制。3)信号时序约束:本文为防止车辆间因相冲突航向而发生碰撞,考虑了以下几个约束。当时间步长p∈Ts下车道l∈L交通信号为绿或黄时,信号时序变量均为1。否则,同时取值零,反映此时信号为红。约束条件(13)可确保在时间步长为p∈Ts时没有一对相互冲突的航向能同时收到非红交通信号。另外,约束(13)也可防止车道信号同时变绿或黄。约束(14)确保车道的绿灯时间小于或等于设定的最大绿灯时间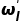 。约束(15)确保车道l∈L的绿灯时间大于或等于最小绿灯时间ωl。约束(16)定义了黄灯持续时间,约束(17)确保在绿灯结束时信号从绿切为黄。参数
。约束(15)确保车道l∈L的绿灯时间大于或等于最小绿灯时间ωl。约束(16)定义了黄灯持续时间,约束(17)确保在绿灯结束时信号从绿切为黄。参数 为黄灯时间间隔。约束(18)保证了信号时序变量的完整性。
为黄灯时间间隔。约束(18)保证了信号时序变量的完整性。
上文所提出的方程组是一个非线性的混合整数规划问题。由于非线性约束和二进制变量的存在,该问题求解困难,难以高效求解。本文首先将目标函数(2)、跟车模型(8)和条件约束线性化以降低其复杂度。此后,使用拉格朗日松弛法将路口级问题分解为几个车道级子问题,这些子问题可帮助降低计算复杂度并且满足车道各自匹配独立信号控制器的特性。各控制器将通过共享拉格朗日乘子协调各信号时序参数和CAV轨迹,确保在满足约束(13)的前提下找到近似最优解。
线性化
目标函数( 2 )的第二项包含一个绝对值函数,该函数为凸但非线性。为了线性化绝对值函数,我们在时间步长 t ∈ Tt 为各车辆引入两辅助非负变量 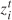 和
和 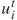 。将约束( 20 )和( 21 )添加到原始问题,使
。将约束( 20 )和( 21 )添加到原始问题,使 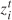 和
和 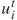 的差等于绝对值项。目标函数( 2 )的线性形式如( 19 )所示,其中额外目标是使辅助变量和最小。约束(8)由于max-min函数的存在为非线性。本文通过将等式约束转换为多个不等式约束并向目标函数中添加惩罚项的方式将这些非线性约束转为线性形式。引入
的差等于绝对值项。目标函数( 2 )的线性形式如( 19 )所示,其中额外目标是使辅助变量和最小。约束(8)由于max-min函数的存在为非线性。本文通过将等式约束转换为多个不等式约束并向目标函数中添加惩罚项的方式将这些非线性约束转为线性形式。引入 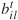 ∈ Rn 来表示max-min函数(8)中的min部分。值得注意的是
∈ Rn 来表示max-min函数(8)中的min部分。值得注意的是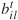 与加速度的单位相同( ft / s2 )。如约束(22)-(25)所示,约束(8)的min部分由以下不等式组表示约束(2 6 )-(2 7 )松弛了函数(8)的max部分,将其用大于等于不等式表示。上述的线性约束(2 2 )-(2 8 )太过宽松不能等效表示(8)的max-min形式。为了解决该问题,本文在目标函数中惩罚系数M调节
与加速度的单位相同( ft / s2 )。如约束(22)-(25)所示,约束(8)的min部分由以下不等式组表示约束(2 6 )-(2 7 )松弛了函数(8)的max部分,将其用大于等于不等式表示。上述的线性约束(2 2 )-(2 8 )太过宽松不能等效表示(8)的max-min形式。为了解决该问题,本文在目标函数中惩罚系数M调节 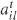 和
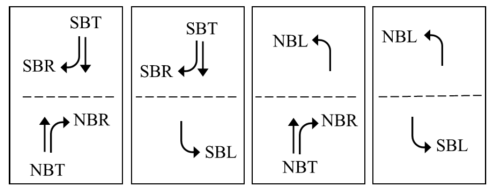
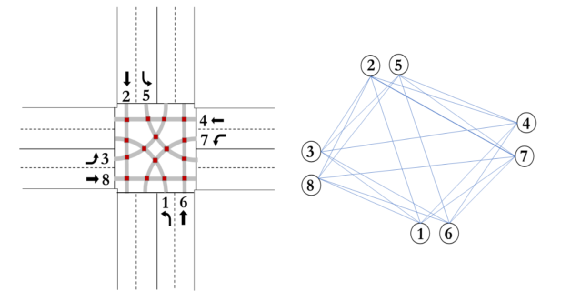
和 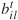 差,由(29)表示。同时采用同样方法线性化(7)。上节的约束线性化可将混合整数非线性规划问题(MINLP)转换为混合整数线性规划问题(MILP)。虽然此方法降低了问题复杂度,但其中的整数信号时序和其他变量仍难以处理。而本文开发了一种拉格朗日松弛方法将问题分解为几个车道级优化子问题。这些问题并行分别搜索最优信号时序和路口上各车道的车辆轨迹。1)问题重构: 成对约束(13)是车道间唯一的共同约束,其目的是防止相冲突航向同时接收到非红灯信号。原问题的车道级分解是通过松弛约束(1 3 ),并借助拉格朗日乘子将其添至目标函数实现的。而划定定义整数解凸壳的超平面可克服松弛后求解失败的问题,同时使解满足上述成对约束。成对的冲突约束可由一个包含边{ i , j }∈ E 的无向冲突图 G =( N , E )表示。E为合理边的条件是对应两二进制节点中至多一个在MILP解中取为1。图4展示了具有四向八车道包含针对左转的路口冲突图。图的节点为与车道 l ∈ L 关联的信号起始点,各边表示(13)的成对冲突约束。定义
差,由(29)表示。同时采用同样方法线性化(7)。上节的约束线性化可将混合整数非线性规划问题(MINLP)转换为混合整数线性规划问题(MILP)。虽然此方法降低了问题复杂度,但其中的整数信号时序和其他变量仍难以处理。而本文开发了一种拉格朗日松弛方法将问题分解为几个车道级优化子问题。这些问题并行分别搜索最优信号时序和路口上各车道的车辆轨迹。1)问题重构: 成对约束(13)是车道间唯一的共同约束,其目的是防止相冲突航向同时接收到非红灯信号。原问题的车道级分解是通过松弛约束(1 3 ),并借助拉格朗日乘子将其添至目标函数实现的。而划定定义整数解凸壳的超平面可克服松弛后求解失败的问题,同时使解满足上述成对约束。成对的冲突约束可由一个包含边{ i , j }∈ E 的无向冲突图 G =( N , E )表示。E为合理边的条件是对应两二进制节点中至多一个在MILP解中取为1。图4展示了具有四向八车道包含针对左转的路口冲突图。图的节点为与车道 l ∈ L 关联的信号起始点,各边表示(13)的成对冲突约束。定义 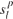 为时间步长 p ∈ Ts 下车道 l ∈ L 的时序参数
为时间步长 p ∈ Ts 下车道 l ∈ L 的时序参数 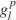 ,
, 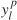 的和。因为绿色和黄色信号至多一个取为1,因此
的和。因为绿色和黄色信号至多一个取为1,因此 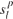 为二进制参数。从冲突图中可见航向的最大冲突航向数量为4,根据此特点可使得凸多边形可行域收紧变小,松弛约束数量减少,对偶间隙减小。2) 简化的STTO和对应的对偶公式: 如上节所述,将约束(13)替换为约束(32)-(34)以得到简化的STTO问题(SSTTO),如下所示松弛约束条件(33)可将SSTTO问题分解为车道级子问题。因此,拉格朗日化的问题是通过约束(33)进行二元化获得的:其中
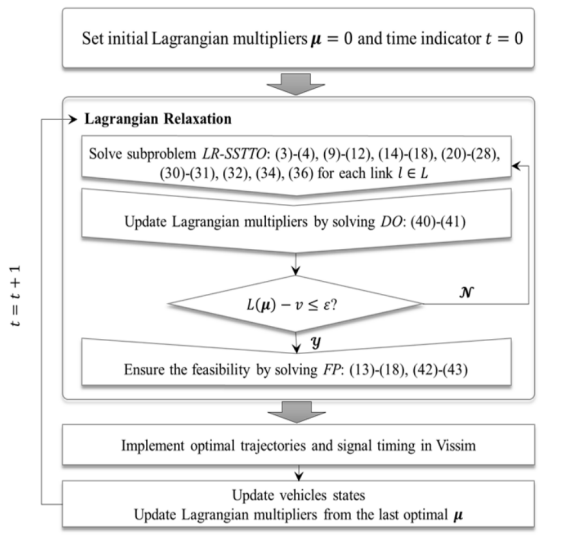
为二进制参数。从冲突图中可见航向的最大冲突航向数量为4,根据此特点可使得凸多边形可行域收紧变小,松弛约束数量减少,对偶间隙减小。2) 简化的STTO和对应的对偶公式: 如上节所述,将约束(13)替换为约束(32)-(34)以得到简化的STTO问题(SSTTO),如下所示松弛约束条件(33)可将SSTTO问题分解为车道级子问题。因此,拉格朗日化的问题是通过约束(33)进行二元化获得的:其中 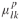 ∈ R + 是时间步长 p ∈ Ts 车道 l ∈ Ck 的拉格朗日乘数。向量 µ 为所有拉格朗日乘数的向量。由于问题 LR 的目标函数和其余约束在各车道上可分离,因此当对偶乘数 μ 可用时,各车道 l ∈ L 子问题可并行求解。可行点 μ 对应的对偶函数 L ( μ )值始终为最优值 f’ 的上限。因此,可从对偶问题最优值( 37 )中找到对应上限,定义为 µ ∗ 。根据对偶理论,对偶问题(37)总为凸。换句话说,如果 f 为有限仿射函数 fi : Rn → R 的最大值,则函数 f : Rn → R 是分段线性凸函数。利用该特征,最佳拉格朗日乘数 µ 可通过双切面法。3)更新拉格朗日乘数: 次梯度法是求解拉格朗日对偶问题更新拉格朗日乘数的常用方法[41],[42]。次梯度方法的特点是仅利用最后一次迭代信息来更新拉格朗日乘数。另外,借助双切面法可记录先前 n 次迭代找到的拉格朗日乘数( µn ),最佳拉格朗日松弛函数 L ( µn )和子梯度 r ( µn ),并搜索新的拉格朗日乘数 µ n + 1 [43]。式(38)描述了各松弛约束次梯度。 正文采用一种基于稳定切面的近端束方法更新拉格朗日乘数[44]。同时在目标函数(40)中添加惩罚项,提升中心点 μcp 附近最佳拉格朗日乘数的稳定性。式中,参数 h ∈ R + 控制着二次项的权重。迭代求解此优化问题可得到一系列拉格朗日乘子{ µn } n = 1,...,N 。4)保证求解成功 :拉格朗日松弛问题最后会收敛至最优解 µ ∗ , g ∗ 和 y ∗ ,并生成所有 CAV 的最佳轨迹。尽管问题的重构可将对偶间隙缩小至很小,但拉格朗日松弛得到的最优解仍可能不满足松弛约束( 33 )。本文在这个情况下引入了一个补充的优化问题 FP ,以确保松弛问题解的可行性,保证求解成功率。FP 中的决策变量为信号时序变量。而 FP 的输入为拉格朗日松弛得到的 g ∗ 和 y ∗ 。 FP 的目标函数是使信号时序变量与拉格朗日松弛相应解间尽可能最小。此外, FP 中考虑了所有信号时序约束,包括松弛的成对约束。只要信号时序 Ts 的预测时域大于路口所有车道的最小绿灯时间,则优化问题 FP 总是可解的5) 滚动时域控制 :为了考虑问题的动态特性,本文将滚动时域控制(RHC)中LR-SSTTO问题相结合。图5展示了了本文的技术框架。首先在时间步长0处初始化拉格朗日乘数。然后,求解每个车道组的LR-SSTTO问题,确定各车道信号定时参数和车辆轨迹。将其解输入 DO 以更新拉格朗日乘数。再通过计算SSTTO问题的上下限差得到问题收敛判据。然后再检查信号时序参数的可行性。若其解无效,则再求解优化问题FP,并根据其可行解更新最优CAV和HV轨迹。若LR-SSTTO的解可行,则无需求解FP,同时该解为原问题的最优解。此后,使用最后一次迭代的拉格朗日松弛解以更新拉格朗日乘数,并且规划时域向前滚动一次,直至结束。
∈ R + 是时间步长 p ∈ Ts 车道 l ∈ Ck 的拉格朗日乘数。向量 µ 为所有拉格朗日乘数的向量。由于问题 LR 的目标函数和其余约束在各车道上可分离,因此当对偶乘数 μ 可用时,各车道 l ∈ L 子问题可并行求解。可行点 μ 对应的对偶函数 L ( μ )值始终为最优值 f’ 的上限。因此,可从对偶问题最优值( 37 )中找到对应上限,定义为 µ ∗ 。根据对偶理论,对偶问题(37)总为凸。换句话说,如果 f 为有限仿射函数 fi : Rn → R 的最大值,则函数 f : Rn → R 是分段线性凸函数。利用该特征,最佳拉格朗日乘数 µ 可通过双切面法。3)更新拉格朗日乘数: 次梯度法是求解拉格朗日对偶问题更新拉格朗日乘数的常用方法[41],[42]。次梯度方法的特点是仅利用最后一次迭代信息来更新拉格朗日乘数。另外,借助双切面法可记录先前 n 次迭代找到的拉格朗日乘数( µn ),最佳拉格朗日松弛函数 L ( µn )和子梯度 r ( µn ),并搜索新的拉格朗日乘数 µ n + 1 [43]。式(38)描述了各松弛约束次梯度。 正文采用一种基于稳定切面的近端束方法更新拉格朗日乘数[44]。同时在目标函数(40)中添加惩罚项,提升中心点 μcp 附近最佳拉格朗日乘数的稳定性。式中,参数 h ∈ R + 控制着二次项的权重。迭代求解此优化问题可得到一系列拉格朗日乘子{ µn } n = 1,...,N 。4)保证求解成功 :拉格朗日松弛问题最后会收敛至最优解 µ ∗ , g ∗ 和 y ∗ ,并生成所有 CAV 的最佳轨迹。尽管问题的重构可将对偶间隙缩小至很小,但拉格朗日松弛得到的最优解仍可能不满足松弛约束( 33 )。本文在这个情况下引入了一个补充的优化问题 FP ,以确保松弛问题解的可行性,保证求解成功率。FP 中的决策变量为信号时序变量。而 FP 的输入为拉格朗日松弛得到的 g ∗ 和 y ∗ 。 FP 的目标函数是使信号时序变量与拉格朗日松弛相应解间尽可能最小。此外, FP 中考虑了所有信号时序约束,包括松弛的成对约束。只要信号时序 Ts 的预测时域大于路口所有车道的最小绿灯时间,则优化问题 FP 总是可解的5) 滚动时域控制 :为了考虑问题的动态特性,本文将滚动时域控制(RHC)中LR-SSTTO问题相结合。图5展示了了本文的技术框架。首先在时间步长0处初始化拉格朗日乘数。然后,求解每个车道组的LR-SSTTO问题,确定各车道信号定时参数和车辆轨迹。将其解输入 DO 以更新拉格朗日乘数。再通过计算SSTTO问题的上下限差得到问题收敛判据。然后再检查信号时序参数的可行性。若其解无效,则再求解优化问题FP,并根据其可行解更新最优CAV和HV轨迹。若LR-SSTTO的解可行,则无需求解FP,同时该解为原问题的最优解。此后,使用最后一次迭代的拉格朗日松弛解以更新拉格朗日乘数,并且规划时域向前滚动一次,直至结束。
图5 嵌入了拉格朗日松弛方法的RHC
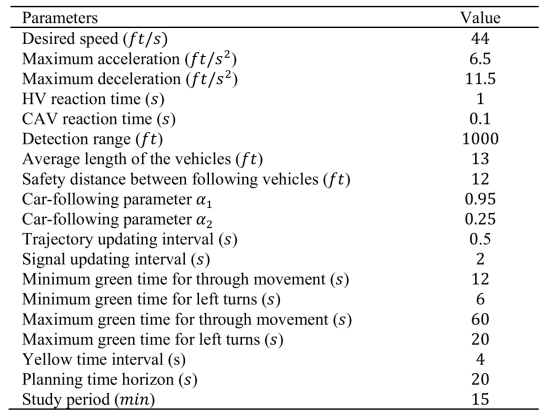
本文在孤立四向路口的左转场景进行研究。如图4所示。假设车辆到达路口前一直处于期望车道。传感器探测范围为路口前后1000英尺。信号状态每两秒钟更新一次,而车辆加速度,速度和位置0.5秒更新一次。RHC的预测范围为20秒。表II展示了更多的详细信息。
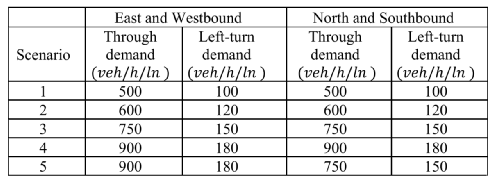
表III为本测试的不同场景。在每种场景下考虑六种不同的CAV比例(0%,20%,40%,60%,80%和100%)。使用Vissim [45]测试本文的算法。使用COM接口收集路网中的车辆信息,并将计算得到的最佳轨迹应用于CAV的运动。算法通过Java实现,并在Intel Core i-9-9900 CPU 64 GB内存的台式计算机上运行。MILP优化问题使用CPLEX [46]求解。
表Ⅱ 案例参数
表Ⅲ STTO案例的交通需求
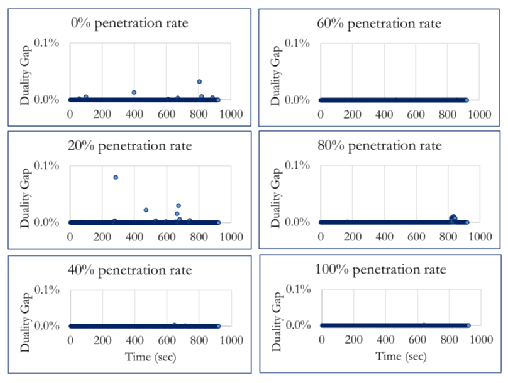
图6 重构问题后拉格朗日松弛的对偶间隙。
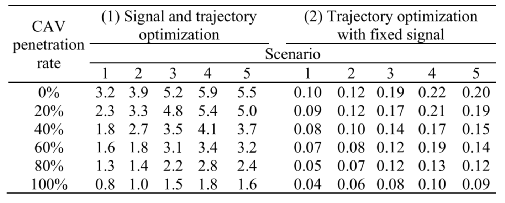
表Ⅳ 不同场景的平均时间消耗
图6展示了场景4下使用拉格朗日松弛法求解STTO的对偶间隙结果,该场景是本研究中交通需求最高的场景。由于借助了滚动时域控制进行求解,拉格朗日松弛问题只需每两秒求解一次。因此,随着时间推移,其可动态求解了所有松弛问题,得到对偶间隙的变化。从图6可看出对偶间隙大部分为零,这意味着本文的解大部分具有强对偶性。此外,结果还表明对偶间隙在场景四的不同CAV比例情况下都始终小于0.1%。
表IV展示了本文模型在场景1至5的平均运行时间。其中平均运行时间包括了两个情况:(1)信号时序参数和轨迹协同优化,以及(2)固定信号时序轨迹优化。在各种情况下,随着CAV比例的提高,优化的时间消耗会减少,因为与HV跟车模型相关变量数的减少。还可看出更高的交通流量意味着更长的优化运行时间。用改进的拉格朗日松弛技术进行信号轨迹优化的平均消耗时间最值分别为0.8 s和5.9 s。应注意的是,由于信号时序参数每2s进行一次优化,因此本文的方法是一种迭代方法,可能无法实时地找到最优解。但可通过改变最优间与信号时序参数更新频率改善方法的实时性。从表IV还可得到使用固定信号参数进行轨迹优化的时间消耗最值分别为0.04 s和0.22 s。
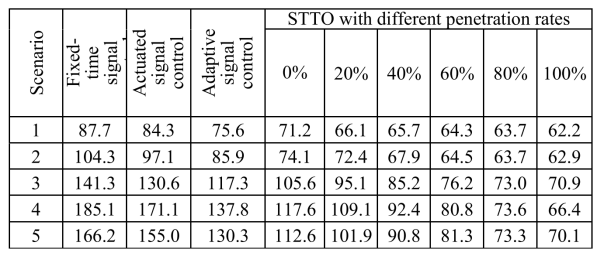
表Ⅴ 不同信号控制器的平均行驶时间(s)
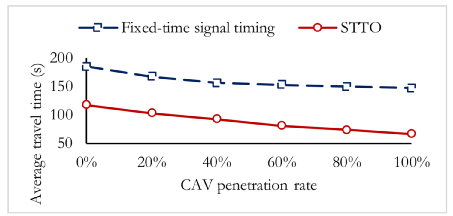
图7 各CAV比例下,STTO与固定时序控制性能比较
表V比较了不同CAV比例下三种信号状态控制方法得到的平均行驶时间:(a)固定时序[47]-[49],(b)驱动式,以及(c)自适应信号控制。固定信号时序控制可看作为基线,其通过对一天不同时间需求的预测进行优化。因此固定信号时序控制无法响应交通需求变化。驱动式可利用车辆检测器对观察到的交通需求变化做出反应。但不能预测短期内的交通情况。而自适应信号控制可预测短期内未来交通状况,并可主动更改信号时序参数。本文在实验中使用PTV Vistro [50]确定最优的固定时间和驱动式信号时序策略。此外,实验中的自适应信号控制方法的实现是基于元胞传输模型[51]-[53]的。结果表明,与固定时序式,驱动式和自适应信号控制相比,STTO的平均行驶时间在不同CAV比例场景下都明显缩短。结果还表明,其平均行驶时间随着CAV比例增加而减少。对于低交通流量场景,这种减少效果不太明显。例如对于场景1和2,CAV比例分别为60%,80%和100%时的平均行驶时间几乎相同。但对于交通需求较高的场景(例如场景4),仍可通过减少所有车辆平均行驶时间来提高路口性能。此外,本文将所提出的S TTO 方法与固定时序式控制在不同C AV 比例情况下进行了比较。从图7可得,就平均行驶时间而言,STTO总是优于固定信号时序。此外,当CAV的比例增加时,与固定时序式相比,STTO的行驶时间减少比例更大。
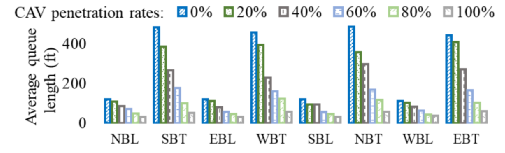
图8 场景4的平均队列长度
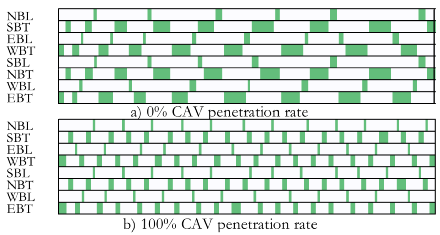
图9 比较0%和100%CAV比例下的信号时序
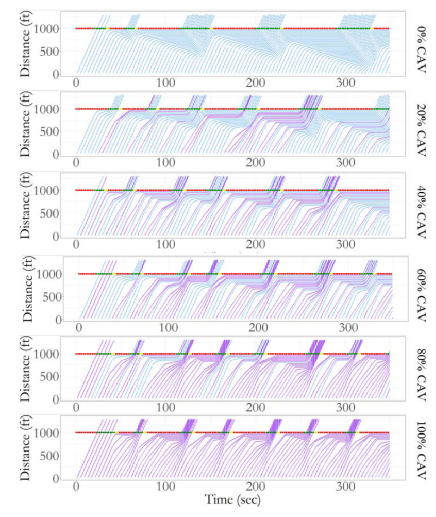
图8展示了场景4的路口在不同CAV比例下所有航向的平均队列长度。可以看到,平均队列长度随CAV比例的提高而减小。而图9展示了场景4下不同CAV比例的某车道所有航向时序。当CAV比例为零时,路口所有航向的绿灯周期更长。这是由于人类驾驶车辆的起步损失时间较大。另一方面,当所有车辆均为CAV时,绿色周期更短,更频繁。这是由于CAV在路口前的停止启动时间较短,并且CAV也会尽可能地以最大速度通过路口。图10展示了不同CAV比例下,东道路(EBT)的CAV和HV轨迹。CAV比例的提高能使得所有车辆以更平滑轨迹通过路口。
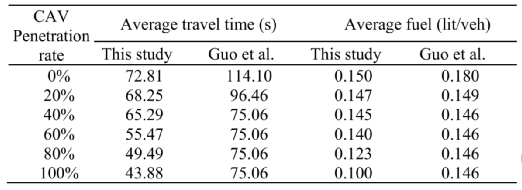
本文将STTO与Guo等人的规划策略进行了比较[3]。这项研究使用动态规划和射击启发算法求解混合环境的信号时序和CAV。结果表明,本文的算法能更快地找到更低的平均行驶时间和燃油消耗。其中,燃油消耗的计算是基于VT-Micro模型[54],其参数与Ma等类似[55]。以下参数设置与Guo等人的研究完全相同[3]:路口长度:1312英尺,饱和率fs:0.6,直行的最大速度:98 ft / s,左转的最大速度:79 ft / s,规划前瞻时间:122 s,跟车参数 :最大加速度= 4.72 ft / S2,最大减速度= 5.48 ft / S2,以及优化信号时序的步长:8秒。
图10 车道1上CAV和HV轨迹
表Ⅵ 与GUO方法比较
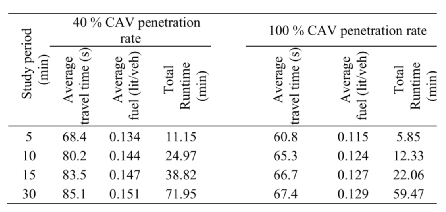
表Ⅶ 不同研究时间的STTO效果
从表六可看出随着CAV比例增加,平均行驶时间和燃料消耗都在减少。此外,本文算法在不同CAV比例情况都要优于[3]的最优结果。值得注意的是郭等[3]假设信号时序有四个阶段。但我们的研究包括了八个阶段,可表示更普通的情况。此外,相位顺序在[3]中是固定的。而本文的相位是没有固定顺序的。
表VII展示了STTO在5、10、15和30分钟研究时间内的平均行驶时间,平均燃油消耗量,总运行时间,并且两个CAV比例分别为40%和100%。表VII中的趋势表明,由于有更多车辆在路网中,因此研究时间的增加会导致平均行驶时间和平均燃油消耗的增加。
这项研究提出了一种针对CAV和HV混合交通流路口的信号配时和轨迹协同优化方法。我们将STTO问题建模为一个混合整数非线性规划问题,并且假设所有车辆均网联,或路口已配备了可提供车辆位置的传感器(例如雷达单元)。HV的轨迹是通过Helly的跟车模型预测的得到的。
由于非线性和二进制变量的存在,该优化问题较为复杂。因此,通过线性化非线性约束,并使用拉格朗日松弛法将路口级优化问题分解为多个车道级子问题的措施从而降低问题复杂度。这样也可利用单个控制器对各车道中车辆进行信号时序和CAV轨迹进行控制。此外,为了减少对偶间隙,还借助可行域的紧凸壳重构STTO问题。针对拉格朗日松弛解可能不满足松弛约束条件的问题,本文又引入了额外的优化问题以搜索高质量的可行信号时序参数。同时,求解方法被嵌入到滚动时域控制中,以反映问题的动态性质。
结果表明,在各测试情况下,本文的方法可成功求解,同时其最优间隙不超过0.1%。同时STTO在不同CAV比例下求得的信号时序均优于自适应控制器的结果,STTO可使平均行驶时间减少5%至51%。此外,提高CAV比例可减少路口处所有车辆的平均行驶时间,这在更高交通需求的场景下更为显著。
本文提出的方法适用于单独考虑左转的路口场景。而将本方法推广至所有路口类型是很有价值的。此外,本研究假设车辆在可检测到的路口范围内不换道,并且也不控制CAV进行换道。因此未来开发用于预测HV变道的算法,并优化CAV的变道决策可进一步改善交通情况。同时,本研究利用了线性跟车模型,而使用更复杂的跟车模型的研究也是未来的方向。更深入地来说,路网中的信号定时和轨迹控制研究也是未来的方向。因为路口间的相互沟通协同决策相对单个路口的应用可进一步改善交通运行和交通安全性。
电话:15221659529
邮箱:20666080@tongji.edu.cn
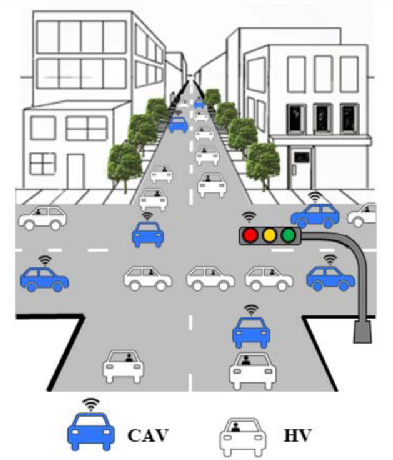
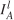 和
和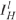 分别表示车道l∈L上所有车辆,CAV和HV的集合。我们将Cl定义为与车道l∈L冲突的所有车道集合。图2显示了孤立路口中定义的集合。
分别表示车道l∈L上所有车辆,CAV和HV的集合。我们将Cl定义为与车道l∈L冲突的所有车道集合。图2显示了孤立路口中定义的集合。 表示将相应参数四舍五入。
表示将相应参数四舍五入。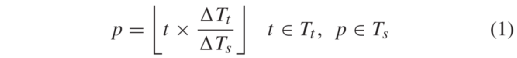
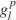 ,黄灯时间
,黄灯时间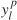 )将基于将近路口车辆i∈Il的位置
)将基于将近路口车辆i∈Il的位置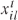 速度信息
速度信息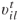 进行优化。时间t∈Tt时车辆i∈
进行优化。时间t∈Tt时车辆i∈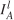 的加速度
的加速度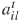 也是CAV运动规划的控制参数。表I列出了问题描述中的变量,集合和参数定义。
也是CAV运动规划的控制参数。表I列出了问题描述中的变量,集合和参数定义。

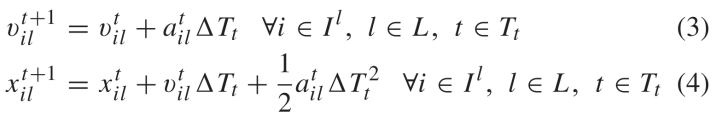

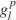 =0,虚拟的停止车辆位于路口停止线χl处,车辆与路口停止线的安全距离为ξ。当绿灯时候,前一虚拟车辆位置将被设为与后车较远的位置,并且车辆到路口停车线的安全距离将减为零。此外,应注意的是仅当车辆位置路口停车线前时,才需要考虑车辆与交通信号灯间的交互关系。在CAV通过路口后,式(6)失效。绿灯时,等式(6)的第二项中将信号时序变量
=0,虚拟的停止车辆位于路口停止线χl处,车辆与路口停止线的安全距离为ξ。当绿灯时候,前一虚拟车辆位置将被设为与后车较远的位置,并且车辆到路口停车线的安全距离将减为零。此外,应注意的是仅当车辆位置路口停车线前时,才需要考虑车辆与交通信号灯间的交互关系。在CAV通过路口后,式(6)失效。绿灯时,等式(6)的第二项中将信号时序变量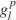 乘以较大系数M,将虚拟汽车移动到与后车较远的位置。这样后车将不再对其作出反应。
乘以较大系数M,将虚拟汽车移动到与后车较远的位置。这样后车将不再对其作出反应。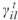 是为了解除车辆通过停止线后与信号灯的连接。
是为了解除车辆通过停止线后与信号灯的连接。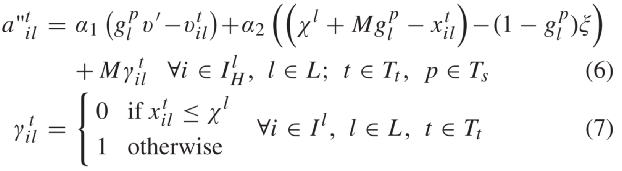
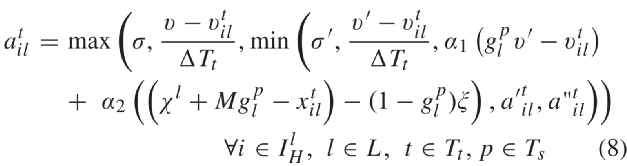
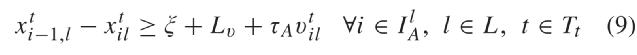
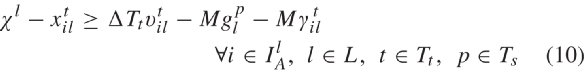
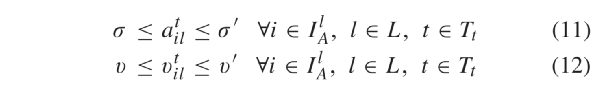
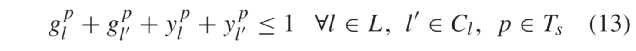
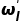 。约束(15)确保车道l∈L的绿灯时间大于或等于最小绿灯时间ωl。
。约束(15)确保车道l∈L的绿灯时间大于或等于最小绿灯时间ωl。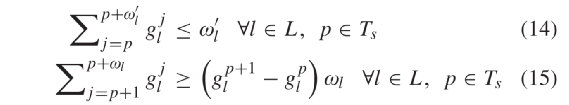
 为黄灯时间间隔。约束(18)保证了信号时序变量的完整性。
为黄灯时间间隔。约束(18)保证了信号时序变量的完整性。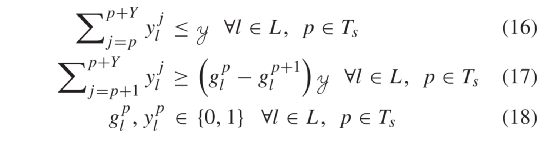
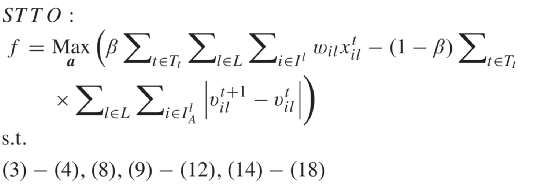
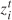 和
和 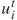 。将约束( 20 )和( 21 )添加到原始问题,使
。将约束( 20 )和( 21 )添加到原始问题,使 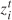 和
和 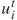 的差等于绝对值项。目标函数( 2 )的线性形式如( 19 )所示,其中额外目标是使辅助变量和最小。
的差等于绝对值项。目标函数( 2 )的线性形式如( 19 )所示,其中额外目标是使辅助变量和最小。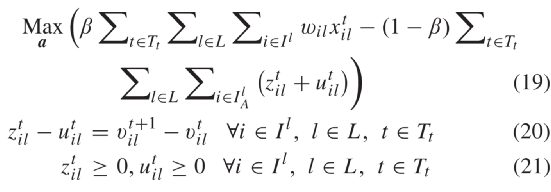
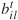 ∈ Rn 来表示max-min函数(8)中的min部分。值得注意的是
∈ Rn 来表示max-min函数(8)中的min部分。值得注意的是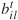 与加速度的单位相同( ft / s2 )。如约束(22)-(25)所示,约束(8)的min部分由以下不等式组表示
与加速度的单位相同( ft / s2 )。如约束(22)-(25)所示,约束(8)的min部分由以下不等式组表示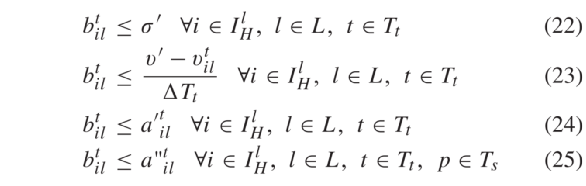
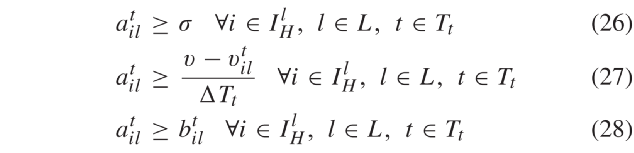
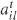 和
和 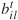 差,由(29)表示。同时采用同样方法线性化(7)。
差,由(29)表示。同时采用同样方法线性化(7)。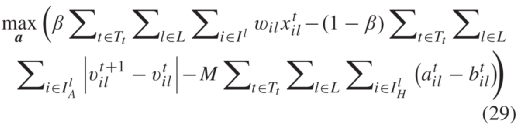
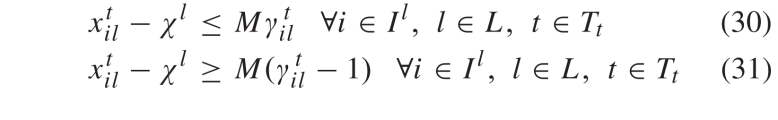
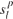 为时间步长 p ∈ Ts 下车道 l ∈ L 的时序参数
为时间步长 p ∈ Ts 下车道 l ∈ L 的时序参数 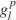 ,
, 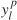 的和。因为绿色和黄色信号至多一个取为1,因此
的和。因为绿色和黄色信号至多一个取为1,因此 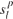 为二进制参数。
为二进制参数。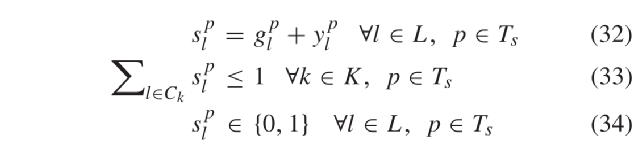
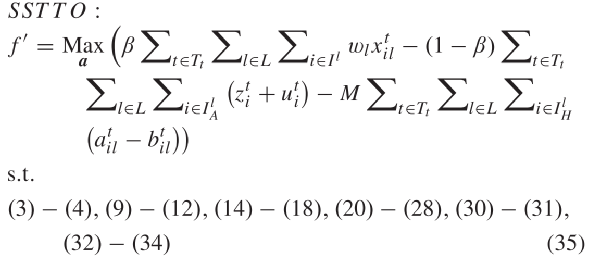
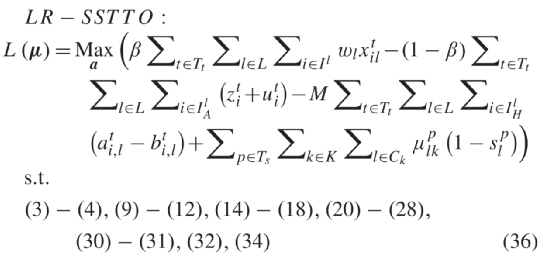
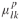 ∈ R + 是时间步长 p ∈ Ts 车道 l ∈ Ck 的拉格朗日乘数。向量 µ 为所有拉格朗日乘数的向量。由于问题 LR 的目标函数和其余约束在各车道上可分离,因此当对偶乘数 μ 可用时,各车道 l ∈ L 子问题可并行求解。可行点 μ 对应的对偶函数 L ( μ )值始终为最优值 f’ 的上限。因此,可从对偶问题最优值( 37 )中找到对应上限,定义为 µ ∗ 。
∈ R + 是时间步长 p ∈ Ts 车道 l ∈ Ck 的拉格朗日乘数。向量 µ 为所有拉格朗日乘数的向量。由于问题 LR 的目标函数和其余约束在各车道上可分离,因此当对偶乘数 μ 可用时,各车道 l ∈ L 子问题可并行求解。可行点 μ 对应的对偶函数 L ( μ )值始终为最优值 f’ 的上限。因此,可从对偶问题最优值( 37 )中找到对应上限,定义为 µ ∗ 。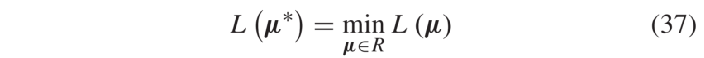
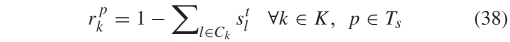
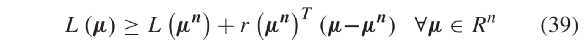
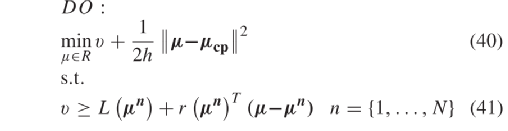
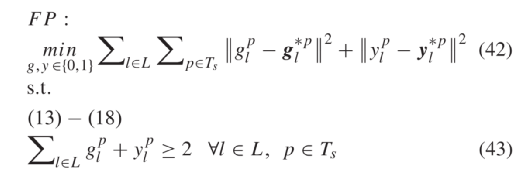












 广告
广告





























































