基于模态测试的车身静刚度识别

车身静刚度是车身结构的关键指标之一，该刚度与各种车辆性能（如NVH，舒适性和车辆操纵稳定性等）显著相关，因此需要对其进行准确的测试。

基于模态测试的车身静刚度识别方法，相比较传统的静刚度台架试验方法，有着诸多优点：比如基于自由-自由边界条件，试验重复性好，能够更好地实现与仿真结果对比验证；另外还可以将结构的模态动力学性能与静刚度性能关联起来，进行各阶模态对静刚度贡献量的分析，等等……

今天将带您深入了解基于模态测试静刚度识别方法的原理，并结合实际工程案例来介绍其实际应用。


前言

识别静刚度特性的传统方法是使用静刚度测试台架，这种方法的劣势是需要专门进行测试台架夹具的设计，夹具设计的好坏直接影响测试结果的精度。另一个劣势在于边界条件很难在CAE环境中进行复现，不利于进行试验和有限元仿真结果的对比分析。

而另外一种方法则是基于车身在自由-自由边界条件下的频响函数测试结果，结合试验模态分析技术，来进行车身静刚度的识别。这种方法的优点是不依赖于任何专业夹具，试验的可重复性好，所需要的测试准备时间也较少。另一个显着的优点是自由-自由的边界条件在CAE环境中更容易重现，从而使得测试和仿真间的关联分析更为容易。唯一需要注意的是，这种方法中所涉及的试验模态分析需要使用者有一定的工程经验，特别是对于内饰车身而言，由于结构阻尼比较大，对于模态参数的识别将更具有挑战性。

这篇文章首先就基于模态试验的静刚度识别方法的原理进行简要介绍，而后分享一个内饰车身的实际工程案例，分析结果将包括车身整体静刚度（弯曲和扭转）和局部硬点的刚度识别。此外，还对车身静刚度结果的稳定性进行分析，验证了这种方法的可靠性。最后，通过模态贡献量分析技术，将车身模态特性与特定区域的静刚度特性进行了关联分析，可以应用于车辆NVH或其它动态性能的优化。

（一）原理介绍

1.1 基本原理

首先回顾一下静刚度的基本测试原理。如图1所示，左图是弯曲静刚度试验原理图，右图是扭转静刚度试验原理图。


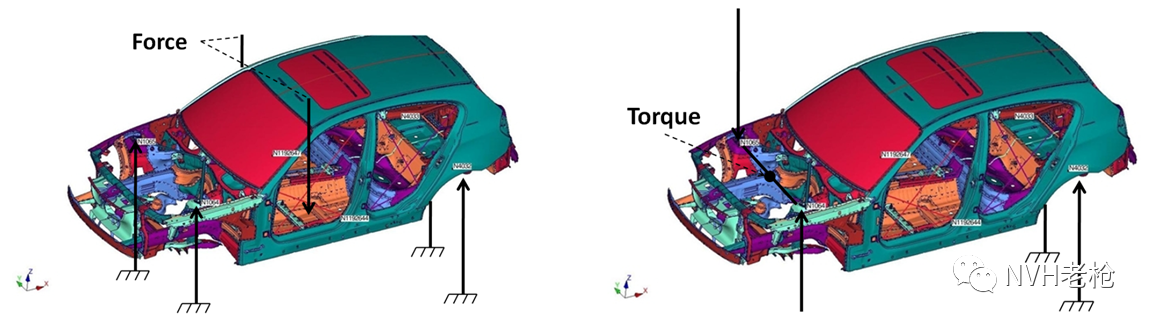
图1 静刚度试验原理图（左为弯曲静刚度，右为扭转静刚度）

对于弯曲静刚度试验，如图2左图所示，首先在车身的前后塔柱点（Shock Tower）位置进行约束（通常前塔柱点仅约束Z向，右后约束X及Z向，而左后则XYZ三方向全部约束）。在左右两侧门槛梁及通道梁上布置多个位移测点，而后在前排座椅位置垂向（-Z）加载。加载力与门槛梁上最大变形量的比值则为弯曲静刚度。对于扭转静刚度试验而言，则如图2右图所示，仅将后塔柱点进行约束，而后在前塔柱点反向施加静态扭矩，加载力矩与扭转角之间的比值即为扭转静刚度。

当加载力作用到车身上后，各个约束都会对车身产生反作用力，对车身本身进行简化受力分析。弯曲静刚度而言，在1，2点施加Z向载荷后，3~6点会产生约束反作用力。扭转静刚度则是在1，2点施加反向载荷，3，4点产生约束反作用力。


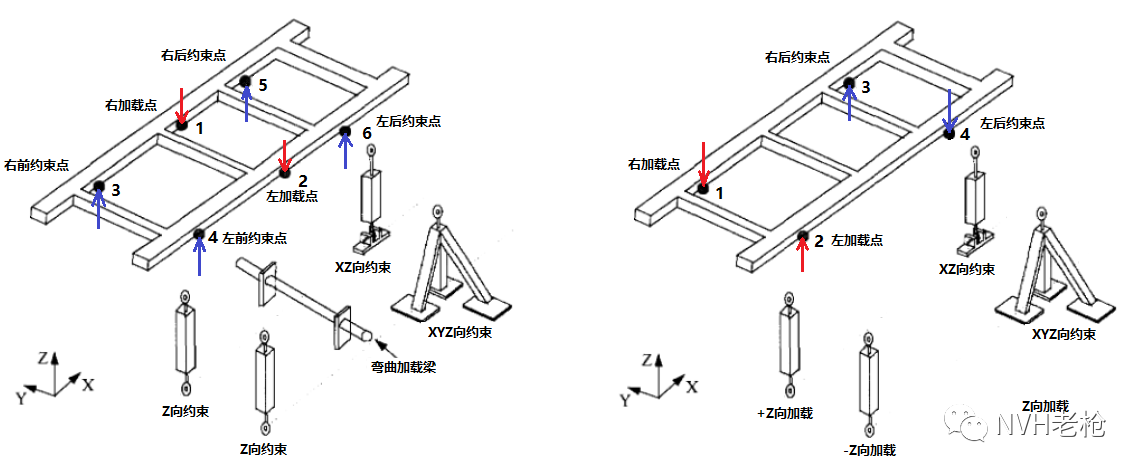
图2 车身静刚度试验受力分析示意图（左为弯曲静刚度，右为扭转静刚度）

就车身结构而言，各个位置的变形实际是由加载力以及反作用约束力共同作用而产生的。如同我们所熟悉的动力学问题，各点的静态变形可以看作是0Hz频率处的位移，也是由各个载荷共同作用而产生：



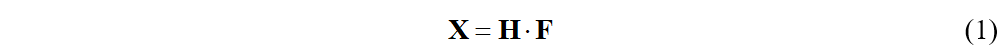
其中为X各点位移向量，F是由所施加载荷以及反作用约束力构成的力向量，H为零频柔度矩阵。

对于弯曲静刚度而言，公式（1）的具体表达形式为：



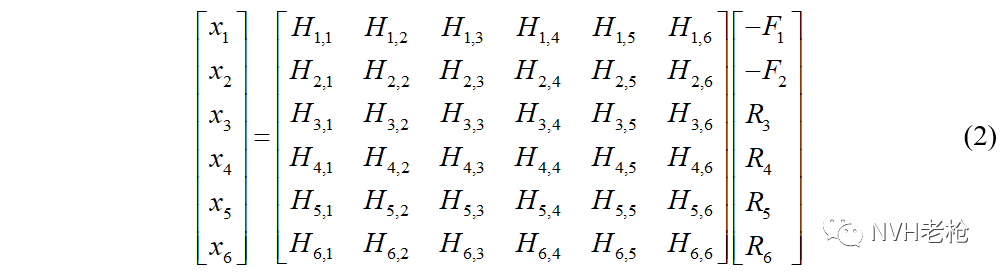
对于扭转静刚度而言，公式（1）的表达形式则更为简单：



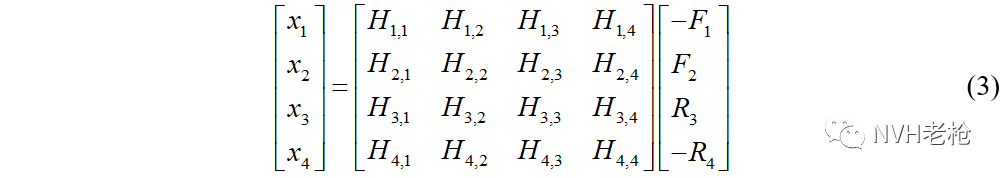
代表外部载荷， 代表约束反作用力，下标为自由度编号。公式（2）只考虑了加载作用点和约束点Z向自由度，而在实际工程中，因为最大变形处不一定在加载作用点，因此通常在门槛梁及通道梁上布置更多的传感器，以捕捉最大变形点。此时公式（2）中的自由度将更多。

如果可以确定出公式（2）和（3）中各自由度间的零频柔度，那么静载荷和静态变形之间的关系就可以确定下来，从而就可以推导出静刚度。

1.2 静刚度的推导方法

静刚度的推导有两种方法，一种是虚拟载荷法，一种是虚拟位移法。

虚拟载荷法

所谓虚拟载荷法就是在车身上虚拟添加一个静态载荷，也就是公式（1）中载荷向量已知，左乘零频柔度矩阵，就可以得到各自由度的静态位移。找到其中的最大变形量（扭转角），除以静载（扭矩）就可以得到弯曲静刚度（扭转静刚度）。


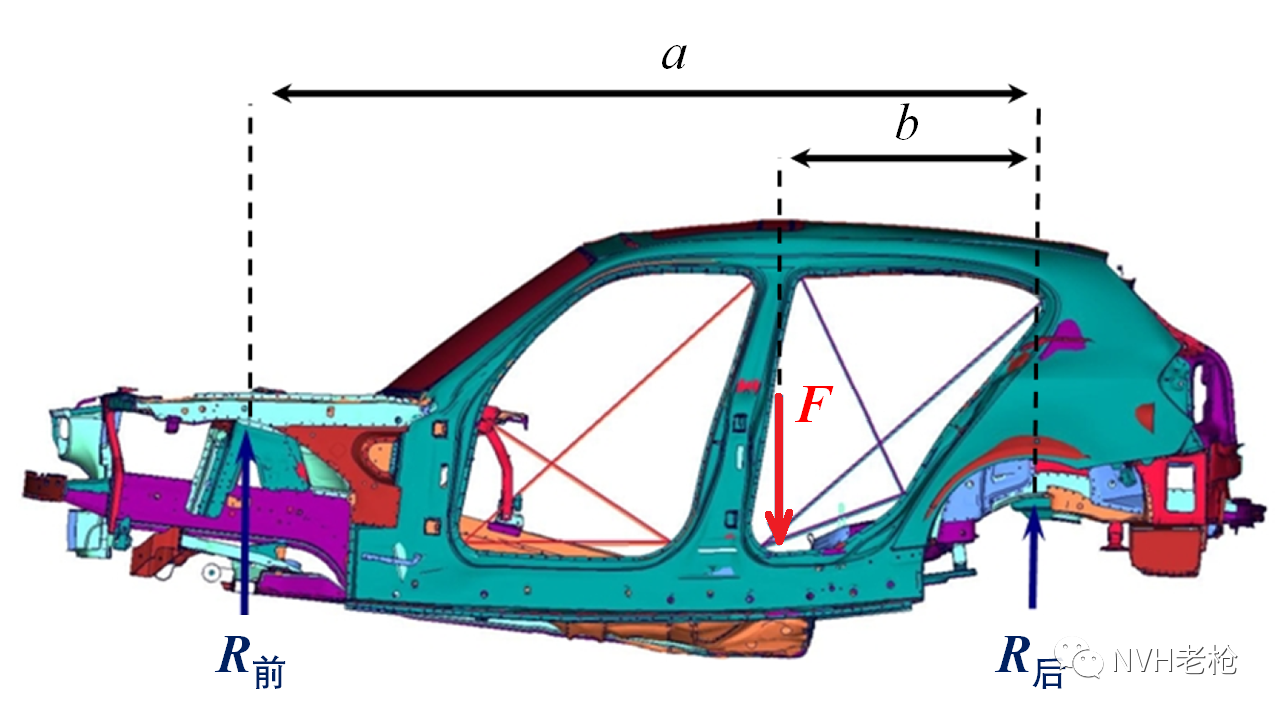
图3 弯曲静刚度试验受力分析

对于弯曲静刚度而言，我们可以根据图3所示几何关系，通过力矩平衡方程推导得到反作用力和外部载荷的关系：


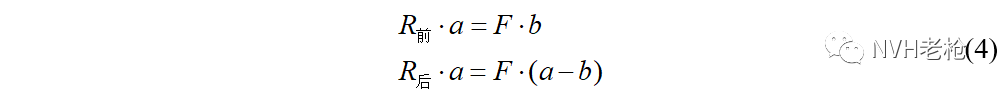
求解，即可得到：



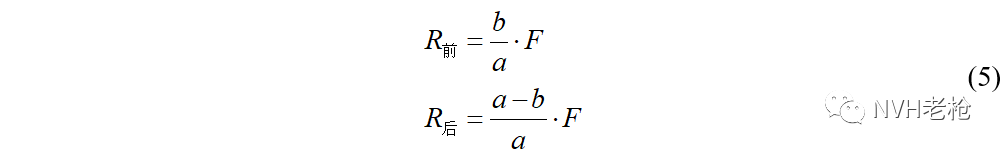
其中 ，。由此，公式（2）就可以简化为：



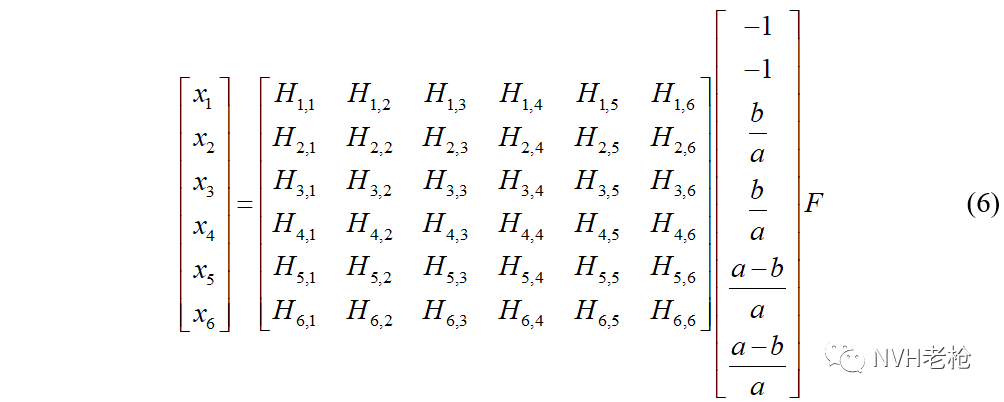
从公式（6）中可以看到，基于车身自由-自由状态下的零频柔度矩阵H，施加虚拟载荷后，就可以计算得到任何载荷作用下各测点的位移，找到最大静态变形点，除以2F  （总外力）即可计算得到弯曲静刚度。

而对于扭转静刚度而言，


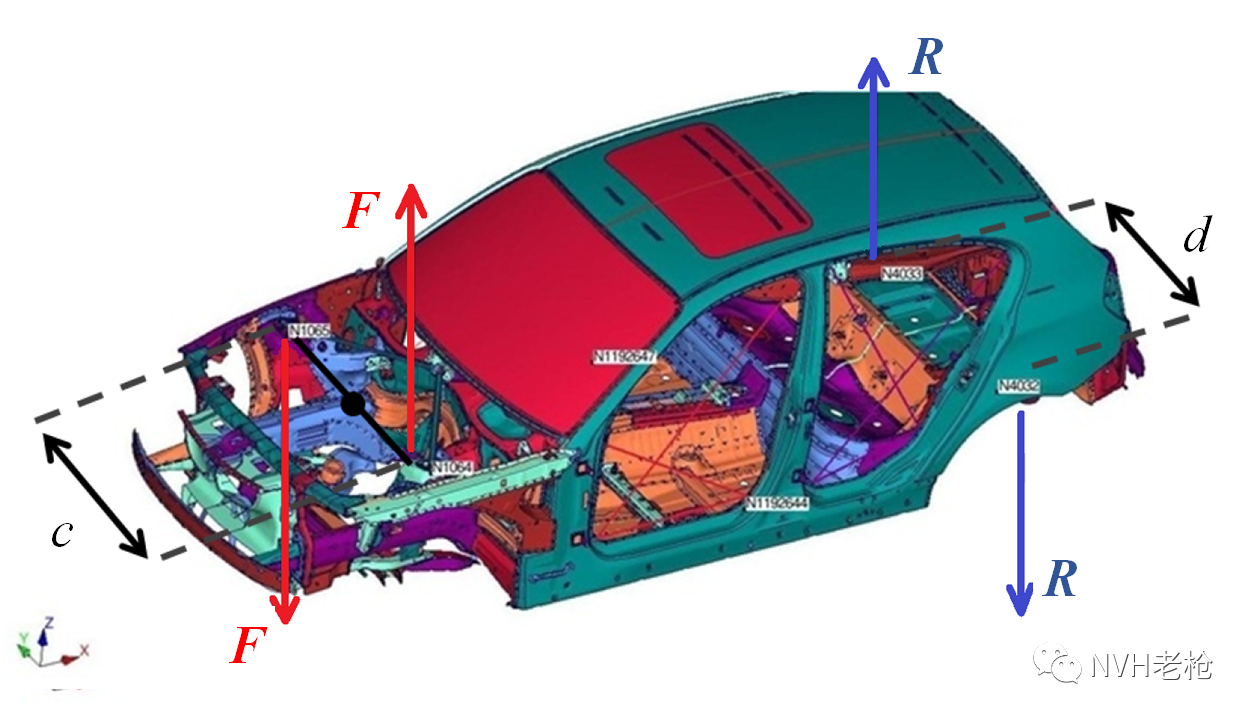
图4 扭转静刚度受力分析

同样，根据图4的受力分析，基于力矩平衡方程：



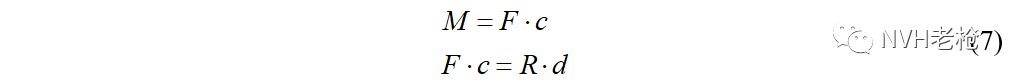
可以得到：



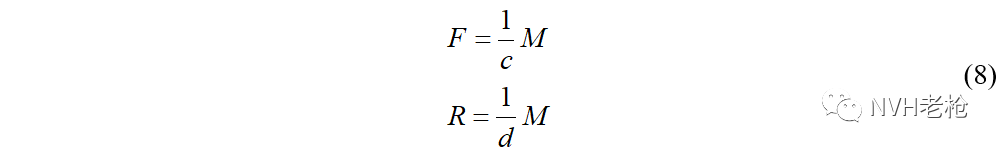
其中 为所施加力矩。由此，公式（3）就可以简化为：



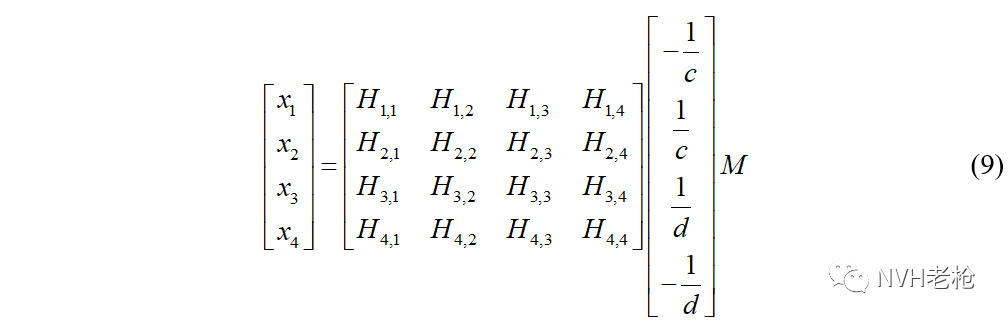
同样基于车身结构的零频柔度矩阵，那么就可以计算得到任何力矩作用下1，2两点的相对位移，从而计算得到扭转角，除以扭矩 就可以进一步得到扭转静刚度。

虚拟位移法

对于虚拟位移法，则是给定车身各自由度一组虚拟的变形量，然后求解所需要的载荷向量。此时公式（2）和（3）改写为：



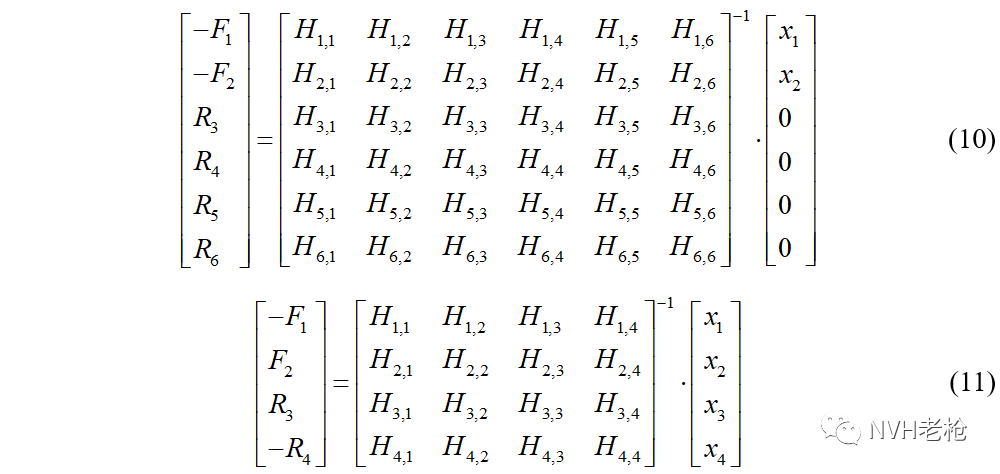
公式（10）考虑到弯曲静刚度试验中3~6点Z向被约束，因此 位移为零。通过给定位移向量，左乘零频柔度矩阵的逆矩阵，求解得到加载向量，就可以计算得到静刚度。因为这是一个矩阵求逆的过程，因此可以想象这种方法对零频柔度的精度要求更高。

（二）零频柔度矩阵的确定

从原理介绍中可以看到，无论是对于弯曲静刚度还是扭转静刚度，无论是用虚拟载荷法还是虚拟位移法求解静刚度，其关键在于车身结构零频的柔度矩阵的确定。对于零频柔度矩阵的确定，目前有两种可行的方法，一种是直接测试法，另一种是模态综合法。

2.1 直接测量法

这种方法希望直接通过测试来得到0Hz附近的柔度矩阵参数。但往往由于边界条件无法实现理想的自由自由状态，导致车身的刚体模态必然会从0Hz向上偏移。此外，如果传感器低频性能不好，也会导致0Hz附近的柔度参数测试结果精度不可靠。

因此所谓直接测量，也通常是通过测试得到的0Hz以上的柔度，然后外推得到0Hz的柔度矩阵。其中一种外推的方法是基于单自由度无阻尼系统假设，对每条频响函数，用较高频率处的高质量频响函数，根据公式（13）列方程组识别出质量 和刚度 参数，然后推导出低频处的频响函数，再外推得到出零频的柔度。测试中可以使用振动加速度计，通过频域积分得到位移。



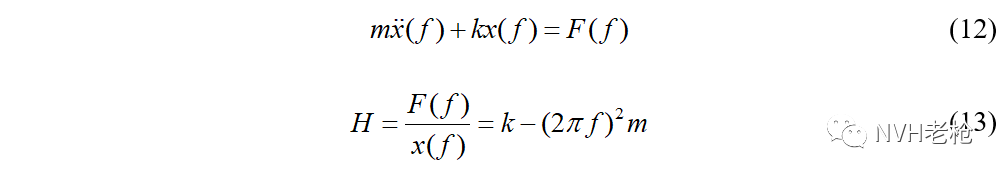
这种方法原理简单，但不能将结构动刚度特性和静刚度特性进行关联分析，无法分析各阶弹性体模态对静刚度的影响。

2.2 模态综合法

模态综合（Modal Synthesis）是NVH工程师所熟悉，大家在做模态试验时，得到模态分析结果后，经常会根据公式（14），用模态综合技术合成得到频响函数，将之与实测频响函数对比，以分析模态分析结果的精度。



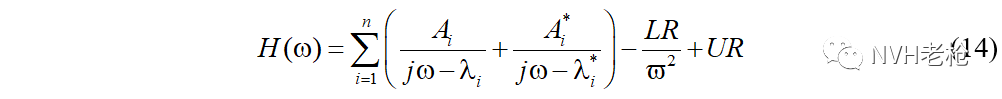
其中 为第 阶模态的极点， 为第阶模态的留数， LR为下残余项， UR为上残余项。

这里利用模态综合技术，是为了通过合成得到各自由度之间的频响函数，频域积分后推算出零频柔度，构造得到柔度矩阵。图5是某结构模态试验中，实测结果（红色）与模态综合（蓝色）得到的频响函数的对比。可以看到，模态综合去除了边界吊挂所造成刚性模态的影响，在300Hz以下，刚度逐渐趋于稳定，直到零频，将零频刚度取倒数即可得到零频柔度数据。


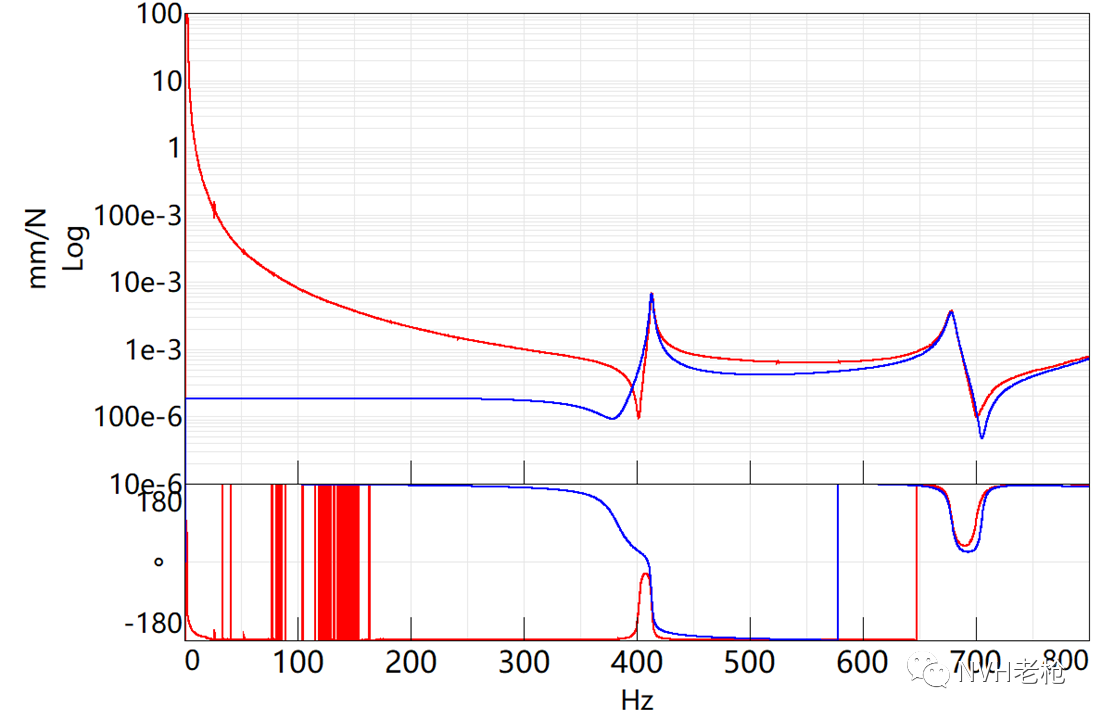
图5 模态综合（蓝色）与实测（红色）动刚度曲线对比

模态综合方法的优势就是基于我们所熟悉的模态分析流程，操作简单方便。但需要注意的是：

•  在模态综合过程中，要充分考虑分析带宽内是否包含了足够多的模态信息。也就是要考虑模态截断对结果的影响，因为分析带宽外的模态同样会对零频静刚度有贡献。如图6所示，白车身不同弹性体模态个数对静刚度识别的影响，可以看到当模态阶数超过47阶后，误差将可以控制到5%以内。

•  当引入的模态阶数比较低时，在模态综合中必须要考虑上残余项。而当模态阶数考虑的足够多时，上残余项的影响将逐渐变小。当达到一定数量后，再引入更多模态的必要性也将下降。越高阶模态越反映的是结构局部刚度特性，因此对整体的静刚度影响就会越小。

•  此外，不同振型的模态对静刚度的影响也不相同，对于弯曲静刚度而言，主要是弯曲模态的影响；而对于扭转静刚度，则主要是扭转模态的影响。


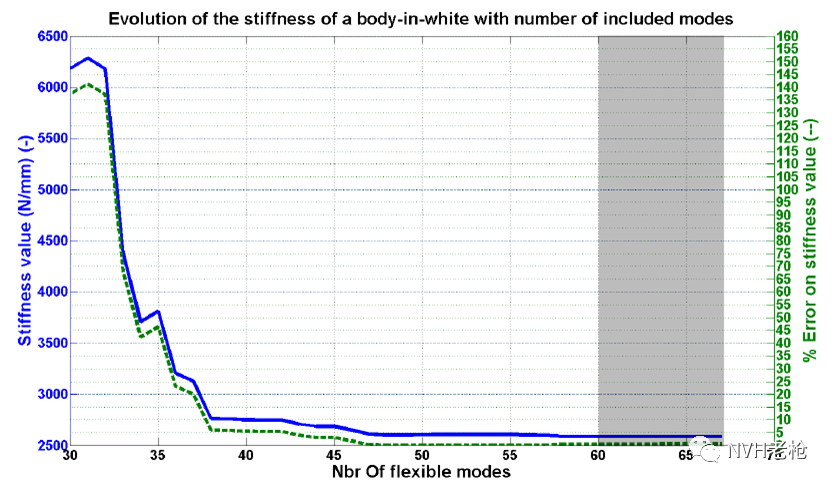
图6 模态个数对静刚度分析结果的影响

（三）工程实例

3.1 车身模态模型的建立

将内饰车身进行软支撑，尽量保证刚体模态和柔性体模态分离。对车身安装硬点进行激励，获取关键位置的响应，从而得到车身的频响函数FRF，为后续建立车身的模态模型做好准备工作。

对于内饰车身来说建立模态模型不是一件容易的事情，因为内饰车身的阻尼比较大，模态密度比较高，所以识别其完整的模态具有一定的挑战。完整的模态模型对于后续柔度矩阵的估计精度是至关重要的，所以我们要尽可能建立一个好的车身模态模型。西门子（原LMS）的Polymax模态分析算法能够很好的应对这种场景，对于大阻尼、高密度的模态分析具有先天的优势。另外，LMS前两年新推出的MLMM模态优化算法，可以通过最大似然估计的迭代求解，更好的完成模态综合中的频响函数拟合，此外还可以比较严格地实现基于实模态的互易性，这对于提高柔度矩阵的精度而言是非常有益的。


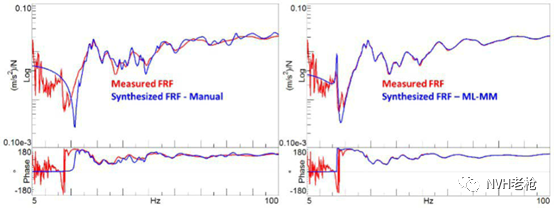
图7 模态拟合曲线和实测频响函数曲线对比

图7左侧结果是手动进行模态参数提取后的拟合曲线和实测频响函数曲线的对比，右侧结果是利用MLMM进行模态优化之后的拟合曲线和实测频响函数曲线的对比，从结果中可以看出MLMM算法优化之后的结果和实测的结果拟合程度要更好一些。

本案例中的内饰车身模态分析的上限频率是100Hz，高于100Hz的模态结果会以残余项的形式呈现。残余项通过MLMM的优化迭代也会更精确，因此拟合出来的曲线和实测结果能够更加吻合。

3.2 车身静刚度的识别

模态模型一旦建立以后，静刚度的计算是通过在模型上虚拟加载，而后求解关键点的位移来实现的，对于弯曲刚度和扭转刚度，只是加载点和关心点的位置不同而已。

目前，西门子（原LMS）的Testlab软件中已经将该功能实现了商业化，其软件界面如图8所示。操作简单，调用模态分析结果后，直接输入虚拟载荷，就可以直接计算出各点位移变形量以及静刚度结果。

此外，如果在频响函数测试过程中，除了静刚度试验中所需要的测点之外，还可以在车身上一些关键的连接硬点布置测点，构建更大的柔度矩阵，这样就不仅可以进行车身整体的静刚度（Global Body Static Stiffness）的分析，还可以得到各连接硬点的局部静刚度信息（Hard Point Static Stiffness）。

软件还支持通过施加不同的载荷（不同位置，不同方向，不同大小），观察车身结构及局部硬点的位移变化，进行各种对比分析。


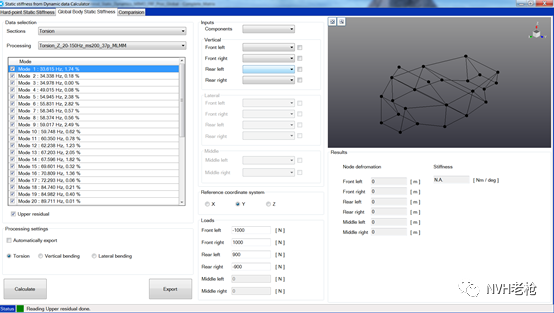
图8 西门子Simcenter Testlab 车身静刚度分析软件界面

为了验证基于模态数据的静刚度试验方法的稳定性，针对同一车身进行了多次模态测试及分析，得到了5组不同的模态分析结果和模态模型。利用5组模态模型的结果对同一个车身硬点位置的静刚度进行估计，如图9所示，可以看到其结果波动量在4.2%以内。


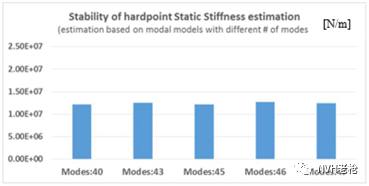
图9 不同模态模型静刚度估计结果对比

为了进一步验证算法的可靠性，针对车身对称位置的两个点静刚度结果进行了估计，按照工程经验，对称位置的静刚度结果应该相当，实际识别结果如图10，其静刚度结果的确相当。


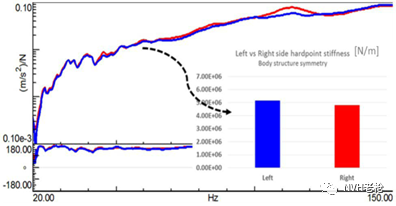
图10 车身对称位置静刚度识别结果

3.3 静刚度结果的分析

通过车身模态模型进行静刚度的识别后，模态分解可以帮助我们更深入的理解车身静态性能和动态特性之间关系。图11列出了车身模态对于前后车身硬点刚度的贡献量结果，从结果中可以清晰的看出关键模态，对于前后硬点刚度来说模态贡献的情况是不同的，正是因为如此，工程师可以明确哪阶车身模态对该区域刚度起着关键性的作用，进而对车身结构进行优化，改善包括NVH在内的各项汽车动态性能。


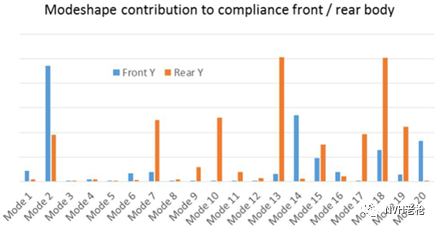
图11 前后车身硬点刚度的模态贡献量结果

此外，还可以结合车身变形与车身载荷、驾驶参数等信息，进行汽车操稳性能分析。如图12所示，是一个100km时速时30°步进转向的工况分析。从图中我们可以看到，在转向的瞬间，前下摆臂前连接点的载荷（红色）立即变大，后下摆臂连接点载荷（绿色）的变化则相对滞后，这是正常的。在整个工况过程当中，可以看到车身的实时变形，以及不同时刻四阶车身模态对车身变形的贡献量（左上图）。左下图显示的是车身上绿色测点的横向变形量，在不同工况时四阶模态对各测点变形量的贡献量则用四种颜色柱状显示。通过这样的关联分析，可以帮助工程师判断车身的关键刚度薄弱点及其对操稳性能的影响。


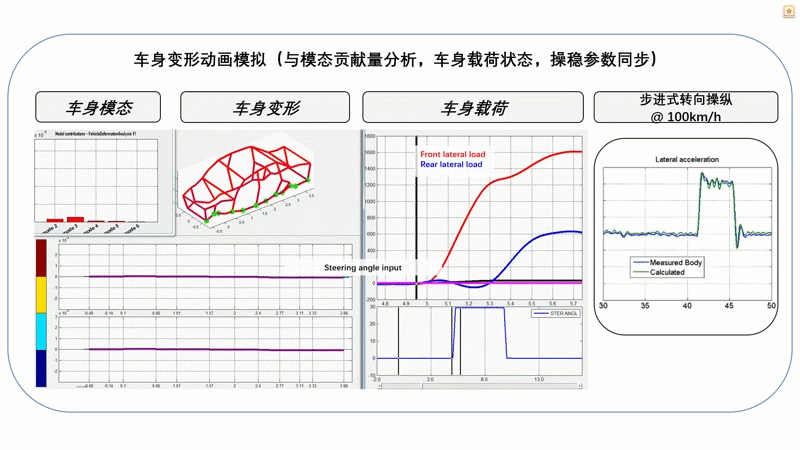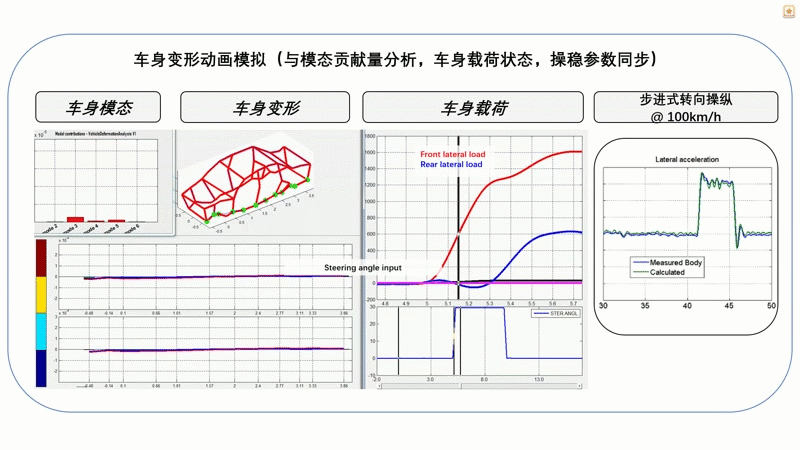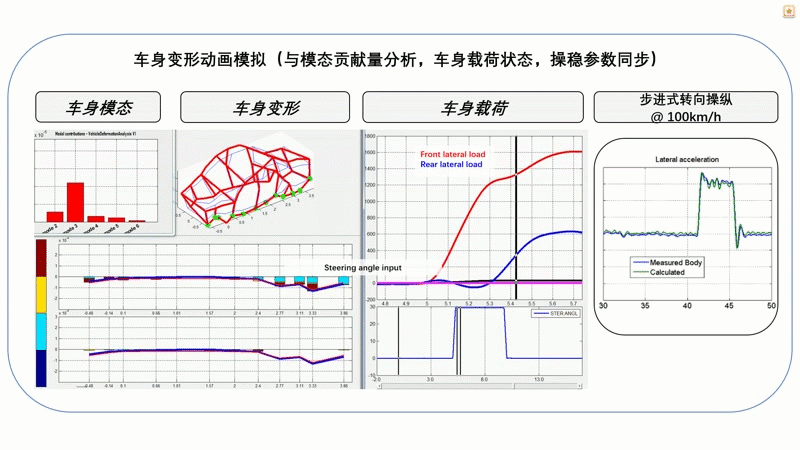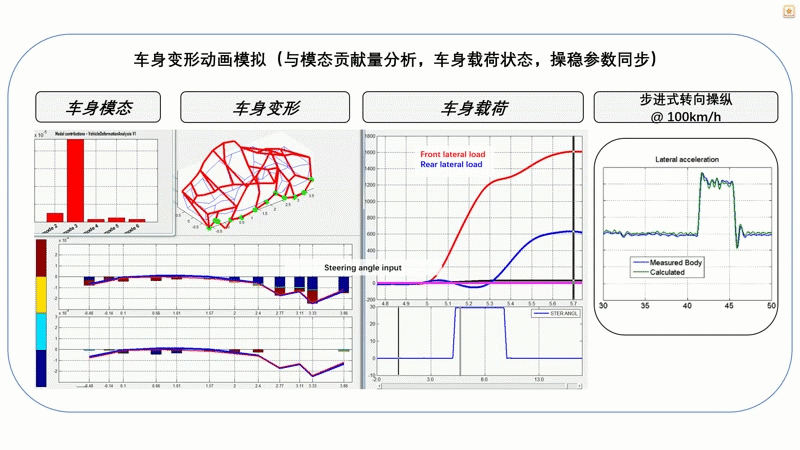
图12 汽车操作稳定性分析

总结

通过车身动态数据（FRF）进行车身局部和全局静刚度识别的方法是一种创新的方法，经过工程实践可以证明此方法的稳定性和可靠性。同时它的运用前景也是十分广阔，不仅可以用于白车身，也可以用于内饰车身。更加难得的是除了静刚度结果外还能延伸出更加丰富和深刻的工程信息，例如利用模态贡献量结果进行汽车操作稳定性分析等。


参考文献
[1] B. Rediers, B. Yang,and V. Juneja, "Static and dynamic stiffness: one test, bothresults," in SPIE proceedings series,1998, pp. 30-35.
[2] J. Deleener, P. Mas,L. Cremers, and J. Poland, "Extraction of static car body stiffness fromdynamic measurements," SAE Technical Paper, 0148-7191, 2010.
[3] J. Helsen, L.Cremers, P. Mas, and P. Sas, "Global static and dynamic car body stiffnessbased on a single experimental modal analysis test," in Proceedings of the International Conferenceon Noise and Vibrations Engieneering—ISMA, Leuven, Belgium, 2010, p. 2.