声场重构技术之二：高阶Ambisonics

王 博 说

上期我们介绍了波场合成技术（Wave Field Synthesis, WFS）及其应用场景，大家是否还有印象？

它成功应用于娱乐场所的空间声重放，例如电影院、歌剧院和体育场馆等。为了追求高质量的声场重构，拓展上限频率范围，往往需要几百通道的扬声器阵列，可谓是“土豪”级的系统。

那么有没有更加实用的声场重构系统呢？

今天我将介绍另一种声场重构技术：高阶Ambisonics（Higher Order Ambisonics，HOA）。

什么是Ambisonics？

Ambisonics是由牛津大学Michael Gerzon在1970年代发展起来的三维空间声场重构技术。想象一下，我们位于一个360°球面的中心，双耳接收到来自球面各个方向上的声音。如果我们记录的空间声场能够以这种方式传输到双耳内，而不仅仅只是前方的两个喇叭，那么会给我们带来更加可信、浸入式的体验，这样的系统就是Ambisonics。

最初，Gerzon等利用无指向性和8字形传声器采集声场的零阶和3个正交方向的一阶信息，得到4路信号（即W, X, Y, Z，称为B-format），然后用扬声器重放出来，这样的系统称为一阶Ambisonics（First Order Ambisonics），现广泛应用于VR游戏、360°视频等。

但是，从准确重构物理声场的角度，一阶Ambisonics只能重构很小区域内的空间声场，空间分辨率也比较低。Jérôme Daniel等发展了高阶Ambisonics，基于空间声场的球谐函数分解，利用一组声场展开系数向量表示空间声场信息。这类似于一个函数的泰勒展开，或者周期函数的傅里叶级数。展开系数的阶数越高，其空间分辨率越高。声场的频率越高，也需要更高阶的展开系数来表示。由于该展开系数是仅与频率有关，而与空间位置无关的一组向量，因此由它表示空间声场具有简洁、计算方便等优点。

举一个例子，自由空间传播着频率为1kHz的平面波，将其在球坐标系下进行球谐函数分解，可以得到不同阶数N的展开系数。如果利用这些展开系数合成平面波的实部，会得到怎样的结果呢？我们看图1，如果用1阶展开系数（即N=1），只能在球坐标系的中心处重构平面波；随着阶数的增大，准确重构平面波的范围越来越大，见图中黄色圆圈部分。


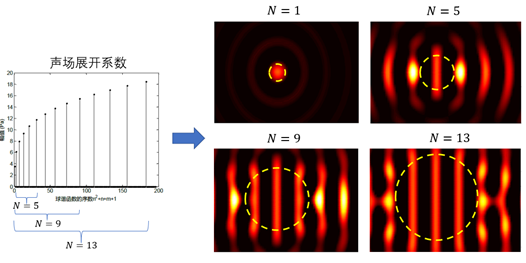
图1

如何采集高阶声场信息？



球形阵列是最理想的采集方式，在球坐标系下对球面声压进行傅里叶变换，即可得到声场展开系数。

球形阵列具有诸多优势，例如：

·  能够有效采集来自于360°方向的三维空间声场信息，非常适合于封闭空间；

·  球形阵列的信号处理更加简单和高效，不同类型的球形阵列可以由统一的表达式描述；

·  由于球面是闭合的，因此球面傅里叶变换不存在传统阵列的有限孔径误差和窗效应，并且球谐函数域本身就是离散的，因此也不存在传统傅里叶变换的卷绕误差；

·  从实际应用的角度，球形阵列的尺寸较小，因此测量更加方便。

常见的商业化的球形阵列有两种：

·  空心球形阵列，即传声器分布在一个镂空的球面上。由于其传声器、线缆和支架等都裸露在声场中，会对原始声场产生散射等干扰。另外，在某些频率点处，空心球形阵列会产生不稳定输出，这被称为球Bessel零点问题，这是空心球形阵列无法避免的。

·  刚性球形阵列，将传声器齐平安装在硬质球壳表面，传声器及其线缆都包裹在球壳内，避免对声场的干扰。球面上传声器测量的声压为入射波与反射波的和，利用球面刚性边界条件可以提取入射波，避免了球Bessel零点问题，在整个频率范围都有稳定的输出。



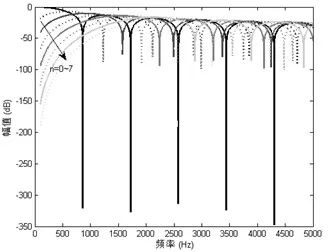
什么是球Bessel零点问题？

这是针对空心球形阵列，其径向函数的幅值在某些频率处接近于零（即上图中的谷值，上图是半径为0.2m的空心球形阵列的径向函数），求逆后会出现极大值，从而导致阵列输出不稳定。

在HBK，我们提供两款刚性球形阵列，直径都为19.5cm，接近于人头的大小，球面传声器分别为36个和50个，如图2，球面上黄金色的小圆点就代表传声器，它们近似均匀分布在球面上。华南理工大学声学实验室曾向我们定制过一个64通道球形阵列，用于空间声重放方面的研究。


图2

有时我们感兴趣的空间范围较大，比如高铁的一节车厢、飞机舱内，或者较大的厅堂，此时球形阵列在一个位置上并不能获得较大空间的声场信息。我们可以用球形阵列分布式测量，比如将球形阵列放在不同的位置，或是多个球形阵列同时测量，然后将不同位置获得的局部展开系数变换到全局坐标系下，如图3。


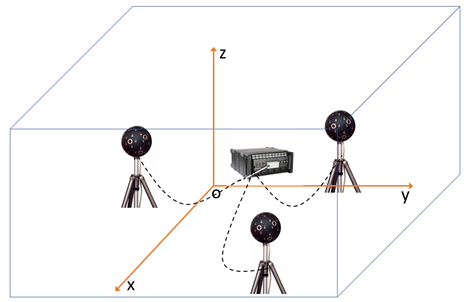
图3

具体计算声场展开系数时，除了球傅里叶变换方法外，还可以建立线性方程组，利用最小二乘法求解。这种方法的好处是对球面传声器的布置没有严格要求，数量也减少了，对测量本底噪声更加鲁棒，因此实际中更加常用。

如果声场在某个基函数（如平面波或球谐函数）下是稀疏的，还可以利用压缩感知（CompressiveSensing, CS）方法求解。例如三维空间的低频声场，体现为声模态的叠加，或者自由空间少数几个声源辐射的声场，都可以探索其稀疏性。利用CS，不仅能够获得更高阶的声场展开系数，还可以显著降低对球面传声器个数的要求。

如何重构真实声场？

高阶Ambisonics的一个显著特点是声场采集和声场重构是完全独立的，在获得高阶声场展开系数后，接下来要做的就是：1）选择合适的扬声器布置；2）把高阶声场展开系数转变为扬声器信号重放出去。

想象一下，如果把扬声器布满整个球面，而我们位于球面的中心处，那么我们就可以听到来自四面八方的声音，不仅可以准确感知声源的方位、距离和大小，还可以体验到更加真实的沉浸感和空间感。实际中，为了达到最高效的布置，可以将扬声器均匀或近似均匀布置在球面上。例如，空间绝对均匀分布的正多面体：正四面体、正六面体、正八面体、正十二面体和正二十面体，将扬声器布置在顶点或面心上，这样可以准确求解出扬声器信号。

如果条件不允许这么布置怎么办？没关系，我们可以综合考虑重构声场的稳定性、准确性和房间实际情况，灵活布置扬声器。比如，在球面不同纬度分层布置，如图4，根据模态匹配方法（Mode matching method）建立线性方程组，计算矩阵的伪逆从而得到扬声器信号，但要注意矩阵的条件数，判断系统是否稳定。


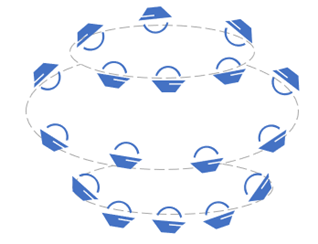
图4

丹麦DTU的Audio-Visual Immersion Lab (AVIL)就依照分层布置建立了一套声场重构系统，由球面上的64个扬声器、4个低音炮和一个头显（Head-mounted Display）组成。它的主要作用是在听音者的周围重构真实声场，研究在复杂多变的环境下人耳的空间听觉特性。丹麦著名的助听器厂商GN也照此建立了一套小型声场重构系统，开展更加真实、可控制和可重复的试验，从而帮助开发更好、更智能的助听器。

更一般地，高阶声场展开系数还可以通过任意的扬声器布置进行重构，例如环绕5.1/7.1声道、不规则布置等。当然，这也面临着很大的挑战，是一个研究热点。

有哪些应用场景？

在商业领域，最常见的应用场景有娱乐场所的空间声重放、虚拟现实VR、360°视频和全景声等。随着消费电子产品的快速发展，家用音响、电脑、手机、TWS耳机等娱乐通讯设备都有可能是潜在的应用场景。值得一提的是，高阶Ambisonics在双耳声重放（耳机、VR头显等）方面有重要的应用，有机会我们再探讨。

在工业领域，凭借高阶Ambisonics的诸多优势，准确重构空间声场（无论是局部空间或者是全空间）可用于

·  助听器、人工耳蜗等的声学研发与性能评估

·  训练模拟器、驾驶模拟器等的真实声场景模拟

·  飞机、高铁等舱内的降噪评估与声品质评价

·  室内声场的可听化


# 参 考 文 献

1. 谢菠荪，空间声原理[M]，北京：科学出版社，2019
2. F. Zotter, M. Frank, Ambisonics[M], Springer, 2019