等几何分析前世今生

01  前奏

要理解等几何分析，首先要了解有限元方法发展的来龙去脉。

达芬奇说过，数学是一切科学的基础。我们所生活的这个世界，大到宇宙天体的宏观尺度，小到肉眼不可见粒子的微观尺度，但凡总结出的原理规律，都可以用一定的数学语言描述；同样，工程中的许多问题都可以用微分方程（常微分方程、偏微分方程）、加以特定的边界条件（力学条件、位移条件、温度条件等）表达。例如，学过材料力学和结构力学的人知道，简支梁的自由弯曲变形可以用以下公式描述：



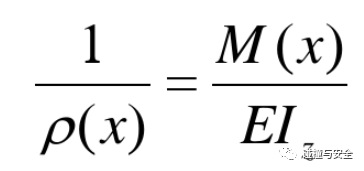
只要知晓施加在梁上的特定边界条件（例如端点位移为0，或受力点载荷值），便可通过求解该常微分方程，精确得到某种工况下（载荷）和梁的弯曲程度（位移/挠度）的关系。


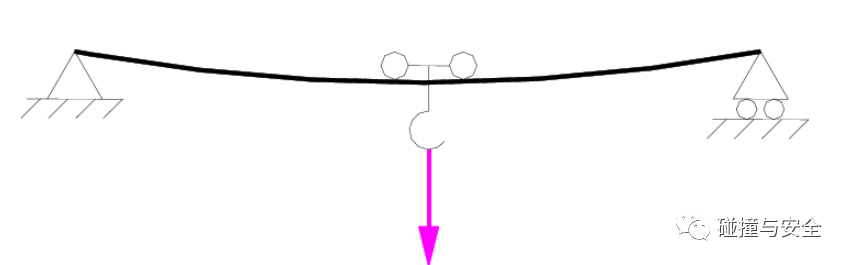
（简支梁的自由弯曲。注：上文公式仅考虑欧拉梁，忽略铁木辛柯梁的剪切效应）

稍微复杂点的，例如求解物体受载后的内部应力/应变，弹性力学告诉我们，可以通过构造三大平衡方程（体现力和位移的关系特性）+物理方程（体现物体本身应力、应变的材料特性）+几何方程（体现位移和应变的关系特性）的闭环系统，外加边界条件，即可联立求解方程组，得到域内任意点的力或位移等信息。


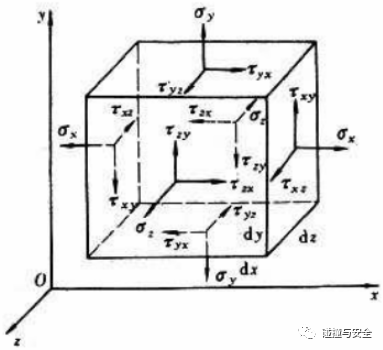
（物体受载内部微观单元体的三向应力状态）

但是，能用公式描述出万事万物来是一方面，进一步能否求解出方程是另一方面。实际上，只有极少数简单边界条件或简化模型，才能通过严格的数学公式推导得到精确解（即解析解）。大多数情况下，我们根本没有办法解出方程，就好比我们描述某个人沿着某条路跑步，知道他用了多久跑了多远，但是无法得到过程中的每一秒他在哪里、速度是多少等等。因此，人们只能曲线救国，通过一定的数值方法求取其近似解。

早在3世纪，魏晋数学家刘徽首创割圆术，是人类数学史上“化整为零”较早的思想萌芽。17世纪，牛顿和莱布尼茨独立提出微积分方法，证明了整体对局部的可加性，从此人们对描述客观世界复杂连续性找到了一个崭新的思路，即化整为零——无穷逼近——化零为整的方法。之后，高斯提出的加权余量法、拉格朗日提出的泛函分析，再到后来瑞利、里兹首次提出对全定义域用位移函数来表述，都对后来的有限元提出建立了理论基础。


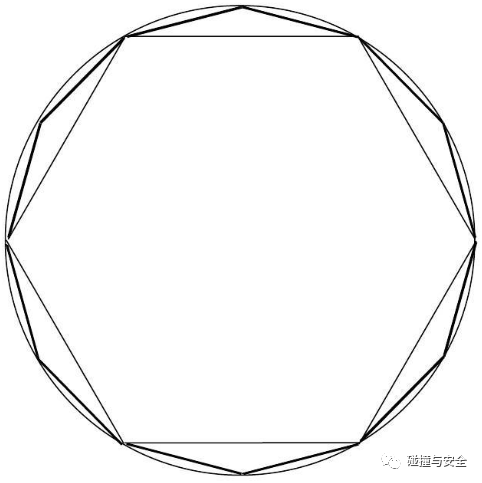
（割圆术：割之弥细，失之弥少，割之又割，以至于不可割，则与圆合体，而无所失矣。——刘徽）

有限元方法（FEM，Finite Element Method）首先应用在航空航天领域。1950年，艾格瑞斯（Argyris）提出力学分析的结构位移方法，被誉为有限元的发明人和创始人；1956年，波音公司在纽约举行的航空学会上介绍了将矩阵位移法推广到平面应力问题的求解上，提出把整个结构划分成一个个三角形和矩形单元进行分析，这实际上就是有限元方法的早期应用；1960年，克拉夫（Clough）首次提出有限元这一术语（《The Finite Element in Plane Stress Analysis》）；1967年，辛克维奇（Zienkiewicz.O.C.，又有人叫杰卡维奇）出版了第一本有限元专著《The Finite Element Method》。与国外有限元发展各阶段同时期甚至更早，胡海昌（广义变分原理）、钱伟长（拉格朗日乘子法）、冯康（先于国外独立提出有限元分析收敛性的理论）等国内学者也对有限元进行了深入研究。随着国内外学者对单元构造、微分方程的数值求解方法、收敛性和精度等有限元基础理论研究的完善，以及计算机算力的提高和相关CAE软件的大力发展，工程上真正开启了有限元方法驰骋CAE领域的时代。


（有限元方法发展的先驱，从左到右：John Argyris——获得16个国家授予的杰出科技与工程奖；Ray W.Clough——美国两院院士，我国外籍院士；Zienkiewicz.O.C.——号称5院院士，我国外籍院士，其撰写的有限元开山制作至今仍是新手入门的不二之选；冯康：中科院院士，我国有限元理论的拓路者。很可惜，以上大佬均未获诺贝尔奖，因为有限元属于计算数学领域，而诺奖不设数学奖。）


（史上第一本有限元著作：《The Finite Element Method》——Zienkiewicz.O.C.）

计算固体力学告诉我们，有限元分析的一般流程为：结构离散（网格划分）——单元构造（确定位移插值方法）——单元分析（局部刚度矩阵）——整体结构分析（所有单元组装成整刚矩阵）——施加边界条件（边值、初值）——构造方程、解方程（数值方法求近似解）。以工程上最常用的平面四节点矩形单元为例，我们选取四个节点的位移作为基本量，其余位置（边界、域内）点的位移通过形函数和四个节点的位移进行双线性插值近似得到：


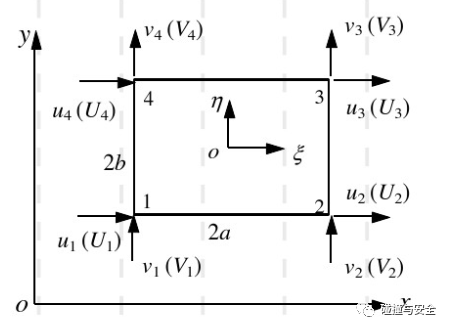
（平面四节点单元，应变为线性）


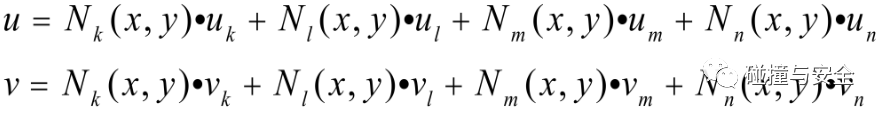
即


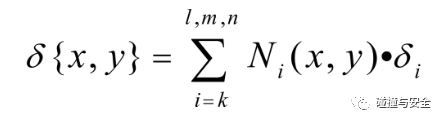
其中形函数为：



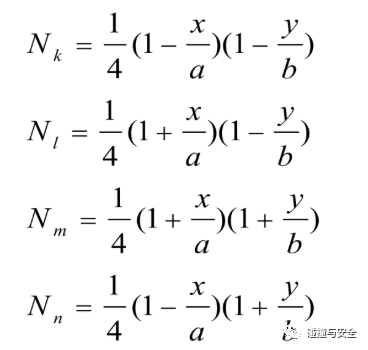
通过某点的位移求导即可得到该点的应变，通过材料本构特性即可由应变得到应力，最终得到以位移为基本量表示的所有力学特性（当然除了四个节点是精确的，其余点都是近似插值得到）。将其代入上文提到过的弹性力学三大方程，即可求解出该单元的刚度矩阵（当然单元刚度矩阵也可由虚功原理或变分原理求导得出，具体不再展开论述）。


（笔者师公所著，有限元和计算固体力学的经典教材）

我们说过，有限元是通过将真实结构离散成很多简单的单元求解的，按照上文得到某个单元的单刚矩阵后，将所有单元的刚度矩阵组装成真实结构的整刚矩阵，再代入边界条件，即可求解出该结构所有单元节点的位移，进而求得所有的力学量。



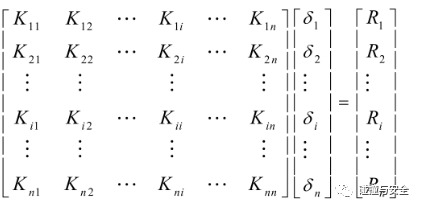
当然，实际工程涉及的模型远比本例复杂，所用的单元类型也不仅限于本例中的平面矩形。以汽车为例，整车离散后的单元个数、节点个数是千万级的，装配所有单元节点后所构造的刚度矩阵，其维数规模远超人力所能计算的范围；不同的单元类型（选择什么样的形函数、什么样的积分点进行插值），决定了求解的精度和效率；不同的矩阵运算和积分算法，决定了刚度矩阵的规模；不同的边界条件和工况，决定了采用何种求解算法（隐式、显示等）。

时至今日，在有限元理论发展和CAE软件高度集成的双buff加持下，今天的工程师已不需要从零开始构造单元、组装矩阵、求解方程（当然这也是不可能的，单靠人力怎么可能求解超大规模矩阵）。我们需要做的，只不过将设计师做好的三维数据，通过前处理工具进行网格划分、选择单元类型和积分方式，然后做点必要的连接、接触等边界条件设置，再丢给求解器进行计算即可，依靠工程经验，几乎不需要过多理解有限元本身的丰富内涵。无论如何，我们所做的所有努力，实质都是在解牛顿第二定律所表示的静力学/动力学方程，只不过公式里的向量是用非常复杂形式的偏微分表示，由于我们无法直接求解方程，只能采用数值方法（有限元），将其转化成有限个单元组成的超大型矩阵运算。其中涉及的矩阵运算、数据存储、方程求解、各种各样单元构造的方式和形函数的推算，其实都凝聚了几代学者的努力，这里就不展开讲了，详情可查阅附录相关资料。



（LS-DYNA中选择某个单元类型，其实就是在选择前辈们为我们推导出的形函数、积分点、积分方式等，不同的单元类型，直接决定了模拟真实物体的力学特性逼真度如何，也导致所得结果的精度和求解效率有很大不同）

为什么要花一些时间介绍有限元呢？因为等几何分析理论的提出，正是伴随着有限元的优势和缺点而诞生的。

02  萌芽

有限元的优势在于，无论多么复杂的形体，都可以离散成简单的单元进行逼近，且边界条件非常容易施加（例如施加本质边界条件，只需约束单元节点的位移即可）。然而这恰恰带来了有限元与生俱来的缺点：Sandia国家实验室曾做过一项统计，工程上80%以上的精力都要用来对模型前处理，即网格划分、单元构造、模型搭建的过程，工程师真正用来聚焦于问题本身和结构优化的时间少之又少；其次，有限元毕竟是一种近似的数值解法，原本连续光滑的模型被硬生生分割成有限个单元，不但精度大打折扣，而且单元之间的光滑性、连续性无法保证，需要后期进行特殊处理；想要提高结果的精度，要么用阶次更高的高精度单元（p-收敛），要么将网格划分的更加细密、更加逼近原始光滑模型（h-收敛），而这无疑增加了人的工作量和电脑的求解时间；不同的网格划分方式、单元类型的选择，直接影响求解精度和效率，工程分析经验性太大，即同一个工况的问题交给不同的工程师来做，可能得到相差甚远的结论；对于大变形问题、裂纹扩展问题等容易产生网格畸变和网格重构的障碍；最后，一旦上游的设计思路变更导致CAD模型更改，有限元模型必须跟着同步更新（例如重新划分网格、重新搭建模型），即伴随不同版本的CAD数据必须同步更新不同版本的CAE模型。

以上所说的每一条痛点，相信在座从事CAE仿真的各位攻城狮都深有体会——每次网格划分质量太差、模型怎么调试都算不通、项目节点逼近又一轮分析任务在等待，都想质问自己一声当初为何脑子进水要从事仿真分析工作。那么，有没有什么方法，能够保留有限元的优势、而又同时解决它的缺点甚至取代有限元呢？

学过数值分析和线性代数的人知道，有限元本质上还是一种解方程的数值方法，除此之外，还有很多近似解法，例如：离散元法（DEM，Discrete Element Method，解决不连续介质问题），边界元法（BEM，Boundary Element Method，只需离散边界，域内无需离散，降维使问题更简单），无网格法（Mesh-less Method，无需划分网格，在边界和域内“撒点”，全局插值），还有有限差分法、有限体积法、谱方法等。但是，须知道任何一种数值求解方法都必须依附于计算机，其中最需要考虑的问题便是效率和精度。尽管当今CAE软件也越来越集成其他的数值计算方法，但这些方法都由于缺乏精度或效率某一方面、或不具有普适性、或实际应用代价太大，终究无法撼动有限元法的霸主地位，仅仅停留在某些特殊问题的研究范围。大多方法，仍然无法摆脱前处理的“魔咒”，即在设计领域和分析领域有一道天然的鸿沟，设计师做出来的模型无法直接交给工程师仿真分析，必须通过前处理打通CAD-CAE之间的桥梁。


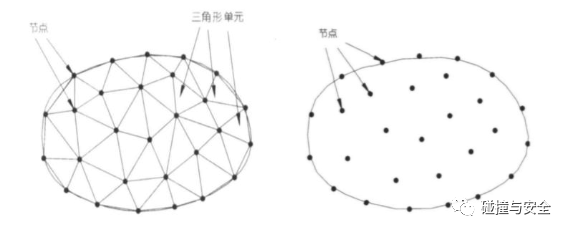
（有限元法（左）和无网格法（右）的模型）

于是，基于打通从CAD领域和CAE领域、使得模型“做出即可用”的想法——设计师画好的CAD模型可以交给工程师直接仿真分析，无需太多的前处理步骤，且具有更高的分析精度、比有限元更接近原始模型的逼近度，2005年，美国德克萨斯大学计算与应用数学系主任、航空航天工程与工程力学教授Thomas J.R.Hughes，提出了等几何分析（IGA，Isogeometric Analysis，又有人叫同几何分析）方法。


（Thomas J.R.Hughes老爷子（左）和他出版的等几何分析经典教材（中）。右图是2018年8月大连理工大学举办的International Symposium on Isogeometric Analysis and Mesh Generation大会上，老爷子精神矍铄的视频连线，祝贺大会召开）

03  真容

IGA是打通CAD和CAE的桥梁，其提出是两个领域理论成果的结合。自然的，除了CAE方面的知识（上文介绍的有限元），还需了解CAD领域的内容，为此先介绍下文的NURBS相关知识。

非均匀有理B样条（Non-uniform Rational B-spline，NURBS），是基于样条曲线（B样条）的有理形式，在大多数工业产品数据交换标准（例如IGES、STEP）中，被作为定义几何形状的主要甚至唯一数学方法。什么意思呢？看下图的B样条曲线：


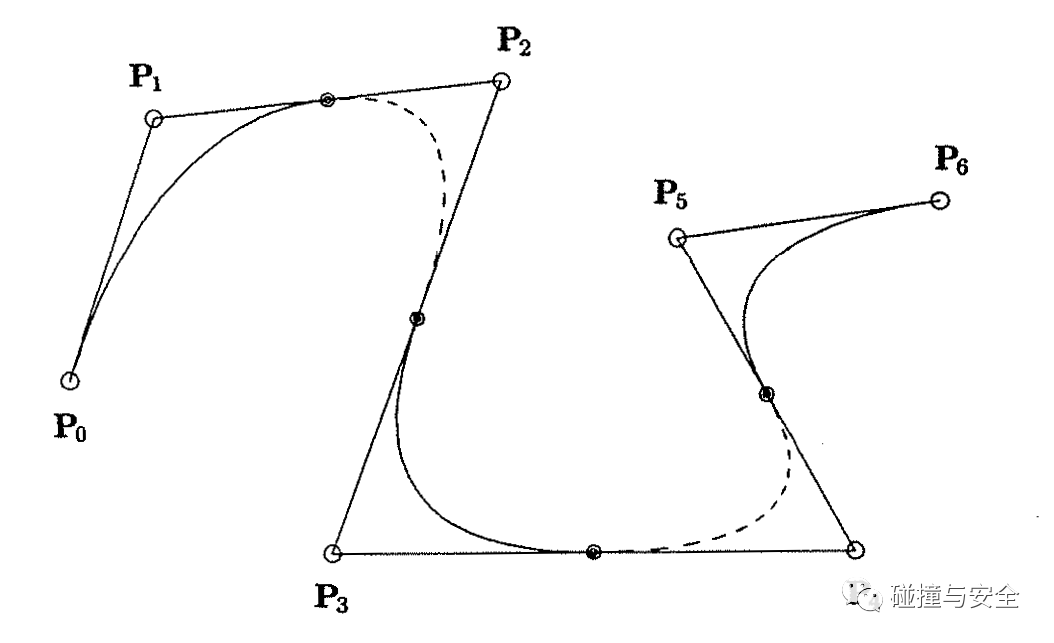
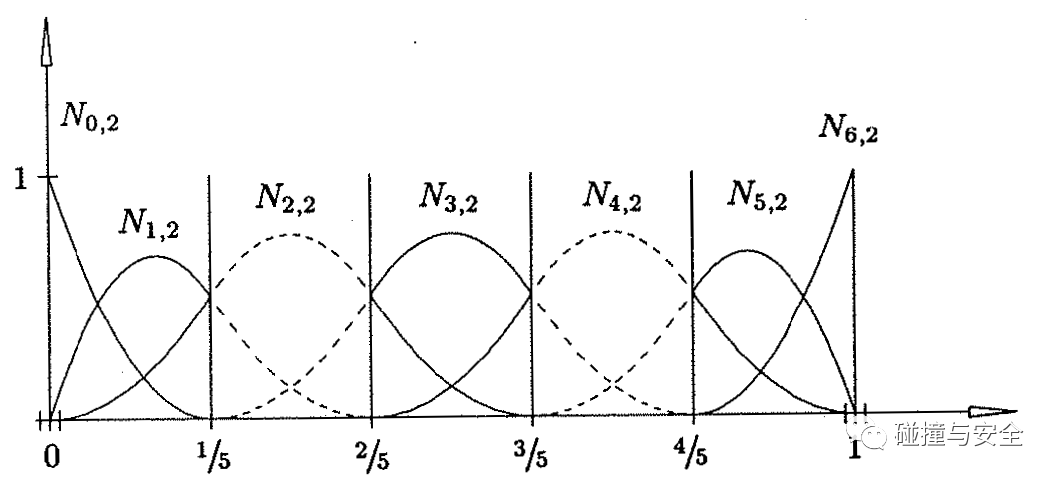
这条曲线的数学形式可以写成参数表示：




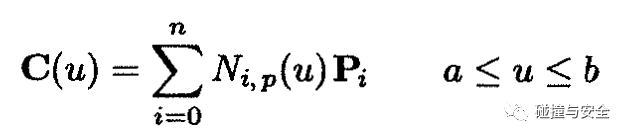
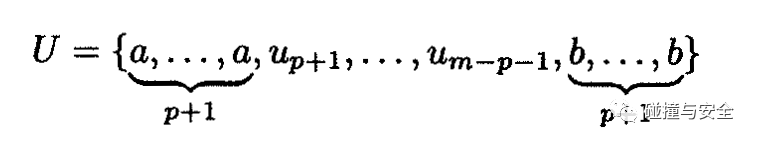
这里需要明确几个概念：

定义域：即参数u所在的自变量区间U∈[0,1]，任意一条参数曲线，都可以定义在[0,1]上，对应的都能计算得到曲线上一点坐标，你可以理解为当自变量u从0到1滑过每个位置，相应的就画出一条曲线。

节点：定义域[0,1]之间划分成不等距的子区间，每个自变量参数ui称为节点。

基函数：即公式中的N。

控制顶点：即公式中的P，也就是图中的包络曲线的P0到P6的控制点。

阶次：即基函数N的下标p。曲线/曲面都是有阶次的，例如：最常见的两点线段是线性，也就是一阶；抛物线以及这里的图示是二阶曲线。曲线阶次越高，表现的越光顺，可导性越高（一阶导为曲线切线，二阶导为曲线曲率）。但是由于人眼可见性，曲线/曲面超过三阶次，人眼很难分辨出来，可是现实中看到阶次更高的形体，会不自觉的感到很舒服，高阶曲面在特定的光影环境中也表现的更为炫丽。飞机高速飞行需要绝对光顺的表面、汽车的造型设计和曲面设计，其实都是围绕这方面做文章。


（飞机和汽车的光顺曲面，极致优美）

具体的计算机图形学知识不需要过多了解（想深入了解的参考下方两本教材），你只需要知道，任意一条复杂曲线或一张复杂曲面，都可以用上述公式这种“基函数×控制顶点坐标”的求和形式描述出来。我们在各种造型软件（CATIA/UG等）看到的所有模型，其底层都是这种数学描述形式，通过一定的渲染和求交技术，最终展现在我们眼前的是可视化的点、线、面、体。


（CATIA的创成式设计或自由造型模块，其中的样条线创建按钮，即为创建样条曲线。此外，做好的数据保存成stp或igs不同格式，其实遵循的就是不同的工业数据交换标准STEP或IGES）

（计算机图形学经典教材：皮格尔著《The NURBS Book》、施法中著《CAGD&NRBS》。CAD领域的发展史，更是一部集数学、数值方法、图形学、几何学、艺术学、心理学等泛领域的精彩史诗，期间涌现出大批牛人，诸如高斯、孔斯、德·卡斯特里奥、贝齐尔、德布尔、考克斯等学者，以及各大软件研发厂商互相吞并、竞争，各种技术相互较量淘汰，最终才有了我们今天高度灵活的造型系统）



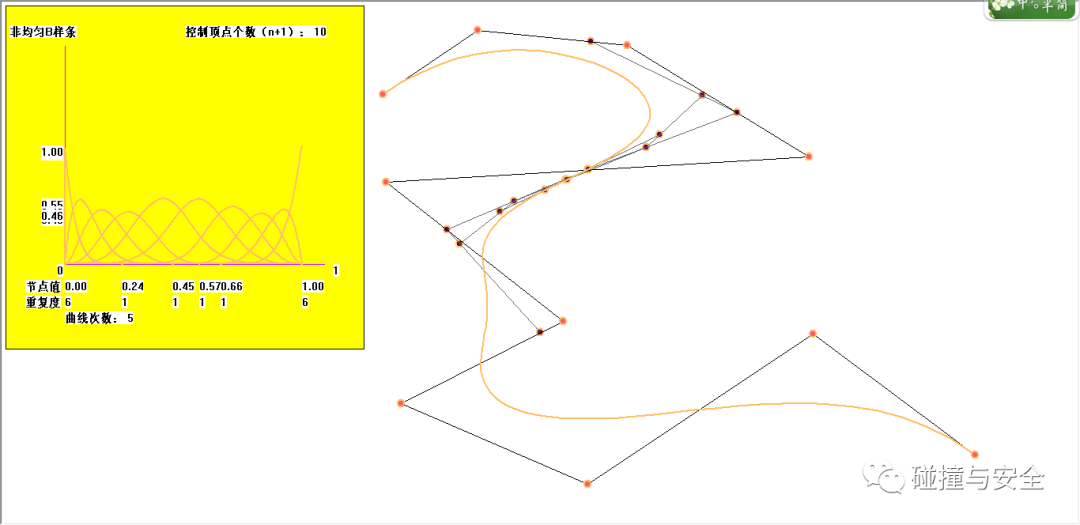
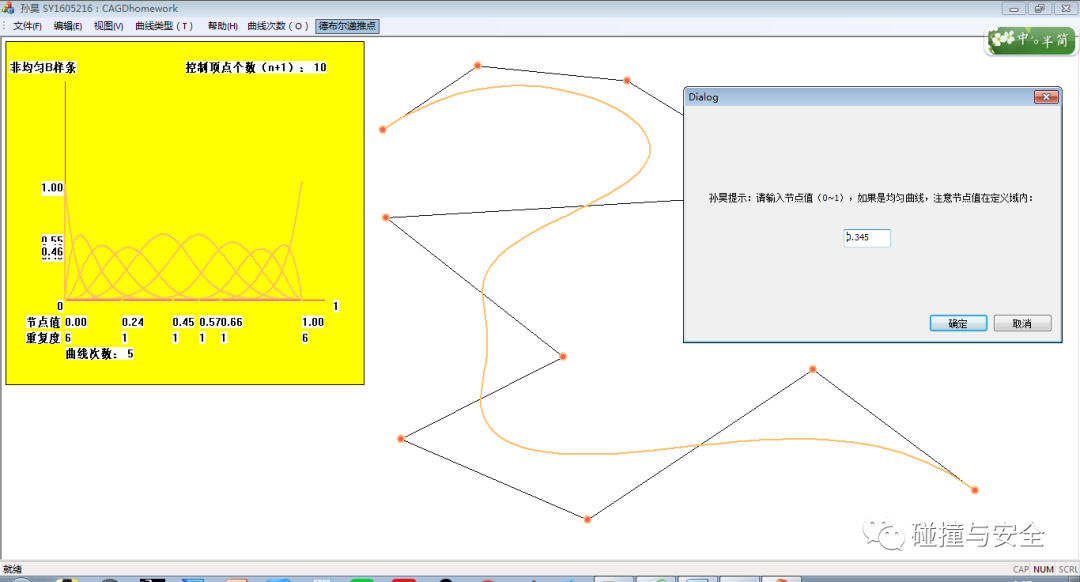
（笔者基于Visual Studio MFC开发的创建NURBS曲线程序，可以实现基于图形区的人机界面自由交互，也能自由对曲线升阶、降阶、增减顶点等）

到这里，细心的读者相信已经发现了，描述曲线/曲面坐标的数学公式，和我们上文中介绍有限元位移场的插值公式，居然如此相似！


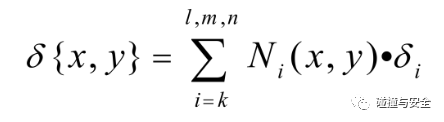
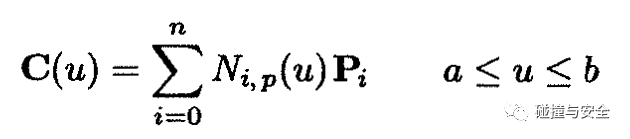
（左：有限元单元位移插值公式；右：B样条参数表达式）

实际上，不只是公式表达形式相似，其所蕴含的物理意义也能一一对应：



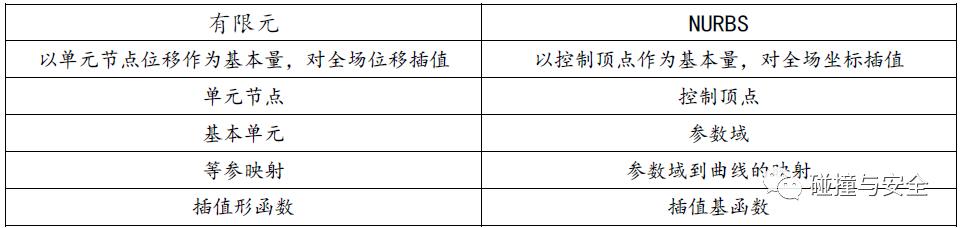
我们知道，有限元单元的特性（单元阶次、积分点、积分形式），完全取决于其插值形函数，即不同的形函数对应了不同的单元类型，你可以简单的认为，一个有限元模型中任意点的位移，都是通过周边节点的位移和形函数加权相乘凑出来的；同样的，对NURBS曲线曲面来说，其特性（阶次、可导性、局部性，仿射不变性）也完全取决于其插值基函数。

为什么有限元分析要先进行前处理划分网格？其实就是把原本的CAD模型（NURBS参数公式）转化成CAE模型（有限元位移插值公式）——比如一张光滑曲面片，在CATIA中使用NURBS公式表述，经过网格划分、单元构造后，原本的光滑曲面被许多线性小单元来逼近拟合，其中每个小单元又可以用有限元位移公式表述，这就完成了从CAD语言到CAE语言的“翻译”。






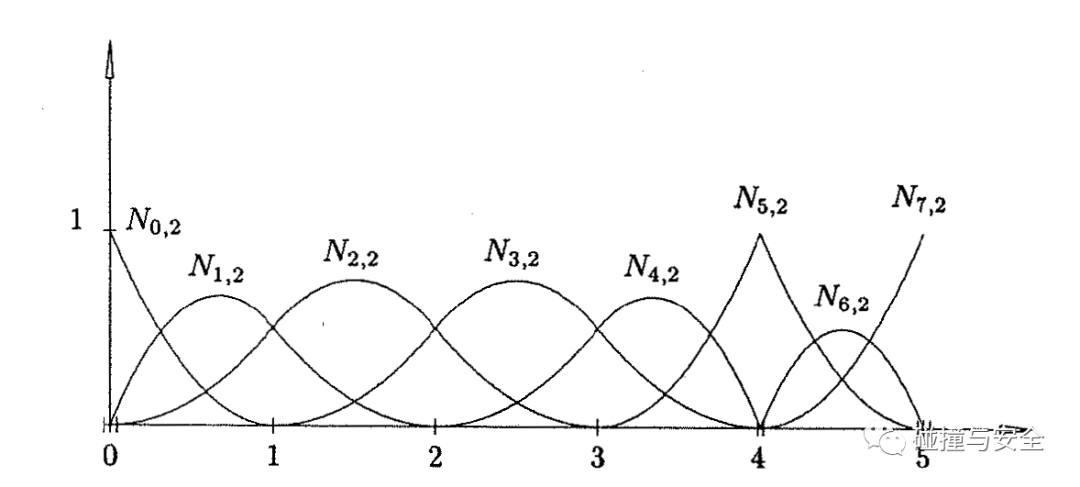
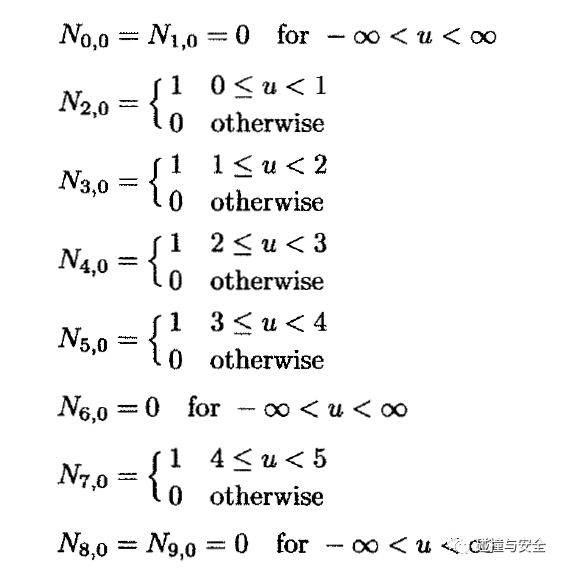
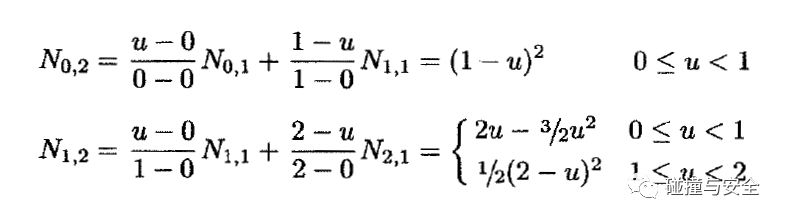
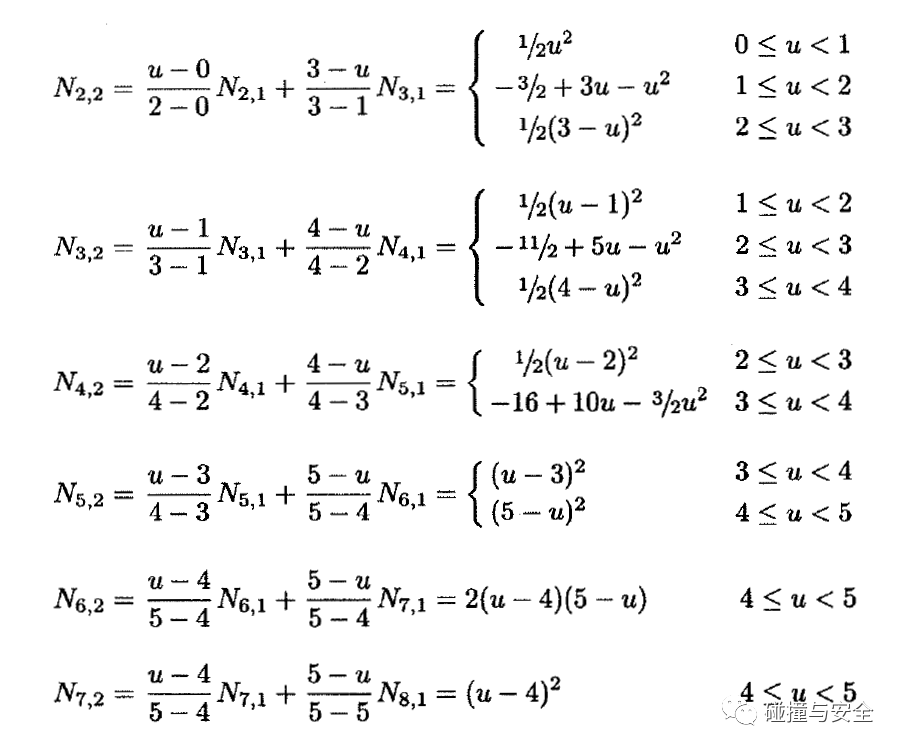
（天才的灵感火花是不可捉摸的，你永远搞不懂多种多样的基函数、形函数，如此简单又复杂的公式，是被怎样发现并推导出来的）

所以，如果能直接用描述CAD模型的数学公式作为CAE模型的公式，不就可以省去“翻译”的过程，帮助工程师从前处理的泥潭中解放出来了嘛？IGA，便是直接将NURBS曲线曲面表达式中的基函数拿来，作为有限元位移场的插值形函数，使得CAD模型和CAE模型具有统一的数学表达形式。

04  发展

可能有人还是不明白，IGA直接利用NURBS基函数作为位移形函数，这有什么用呢？

首先，省去网格划分：不同于FEM每次要将CAD模型离散成很小的网格单元，IGA将原本的复杂曲面分割成一块块的不那么复杂的子级曲面片（patch）。本质上IGA还是基于有限元的“分割”思想，但是，相比较有限元动辄千万个几毫米的线性网格，IGA可以用很少很大的几个patch来逼近原模型，前处理的工作量大大减少。更重要的是，前处理的减负不仅仅体现在某一次的模型分析中，须知实际工程中的模型迭代更新是很频繁的，以汽车为例，往往从预研到SOP期间要经过3到5轮分析，每次分析都意味着有限元网格的重新划分和建模，而使用IGA方法，等CAD模型更新后，其patch也会同步更新（因为patch用的形函数就是NURBS基函数），无需或者简单调整模型即可直接进行分析。


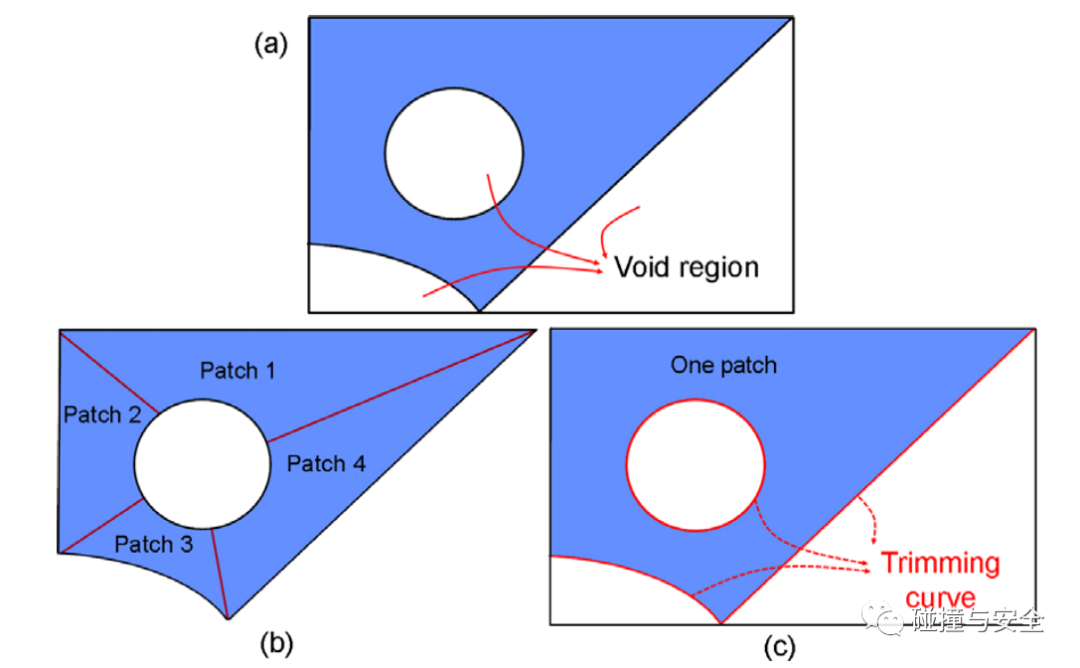
（NURBS子级曲面片，图引自Piegl L A, Tiller W. Geometry-based triangulation of trimmed NURBS surfaces）

其次，几何精确性：由于patch使用了和原模型相同的数学表达式（NURBS基函数），几乎可以说是原模型的“分裂体”，逼近程度非常高；patch之间的连接也能保证一定的光顺性，无需担心有限元单元之间出现的应力不连续、单元畸变，无需在后处理时特意处理单元之间的连接问题。


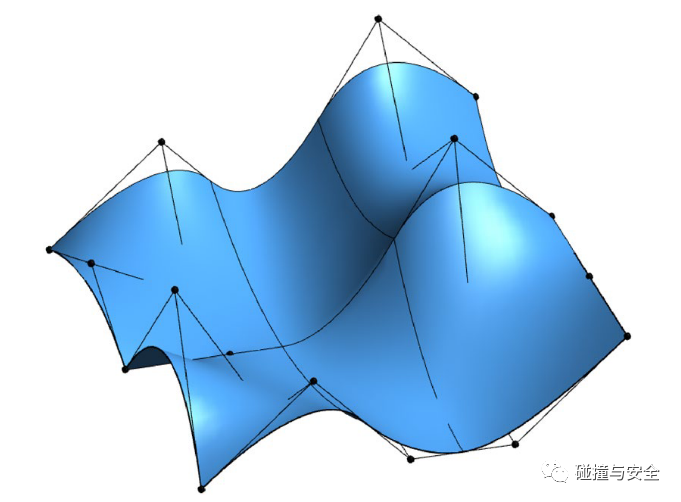
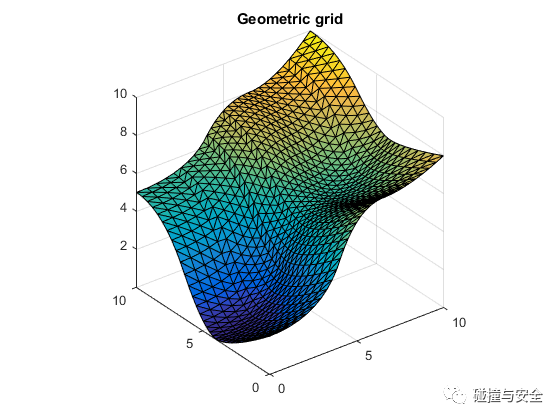
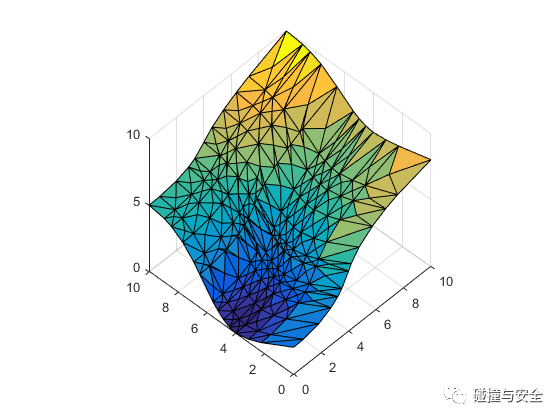
（CAD曲面（左）、FEM逼近曲面（中）、IGA逼近曲面（右））

最后，结果高精度：我们知道有限元要想提高结果的精度，势必要加密网格（甚至重新划分网格），导致计算时长增加。而采用IGA单元，由于NURBS基函数具有天然的局部性和递推性，低阶次的单元可以很方便的构造高阶单元（通过插入节点、基函数升阶或者两者混合使用的方式），这就意味着IGA提高精度无需重新分割成子级patch，无需改变单元本身的形状，这也是“等几何分析”名称的由来。相比较有限元加密网格得到的的h-收敛，IGA通过采用高阶单元得到的p-收敛具有更高的精度。

Hughes最初提出IGA是以NURBS基函数作为有限元形函数，而Bazilevs则证明了IGA具备收敛性和稳定性的特征，这实际上论证了IGA应用于工程实际的可能，从此打开了IGA蓬勃发展的大门。直到今天的短短十几年间，针对IGA的研究成果层出不穷，包括对IGA鲁棒性研究、构造更高精度的单元、应用于相域建模、将IGA和有限元或无网格法耦合分析等。此外，IGA诞生于NURBS的参数表达式，但不同于几何形状的显式或隐式表示，参数曲线曲面并不适合进行复杂的拓扑运算，例如曲面造型中最常见也最难的“求交裁剪”问题：


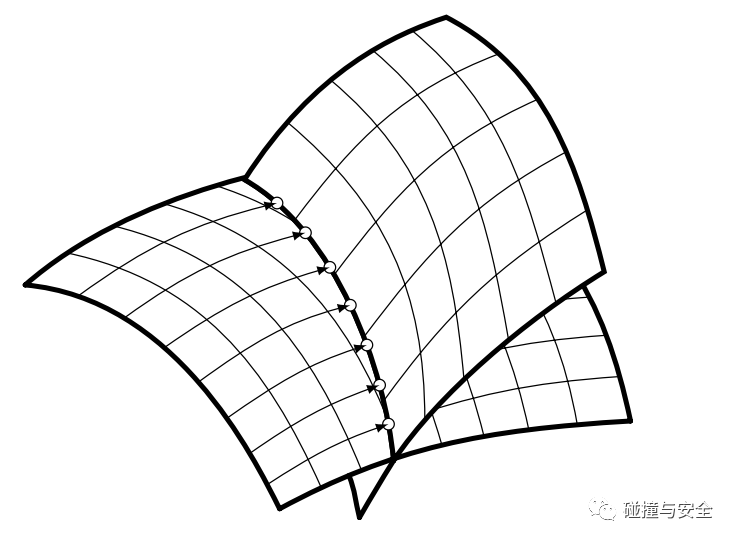
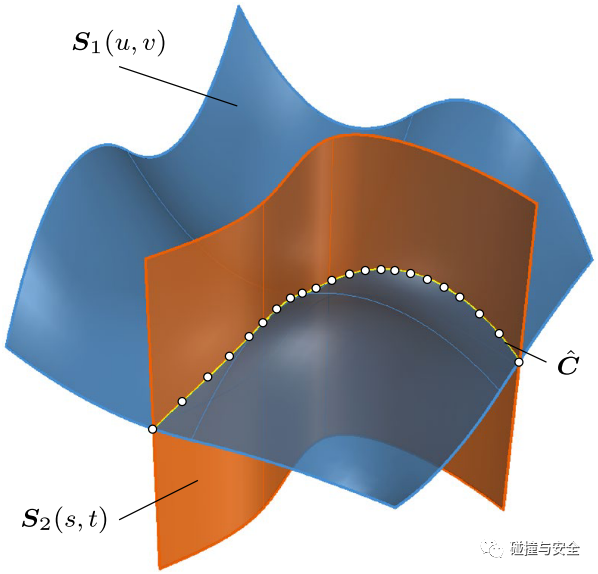
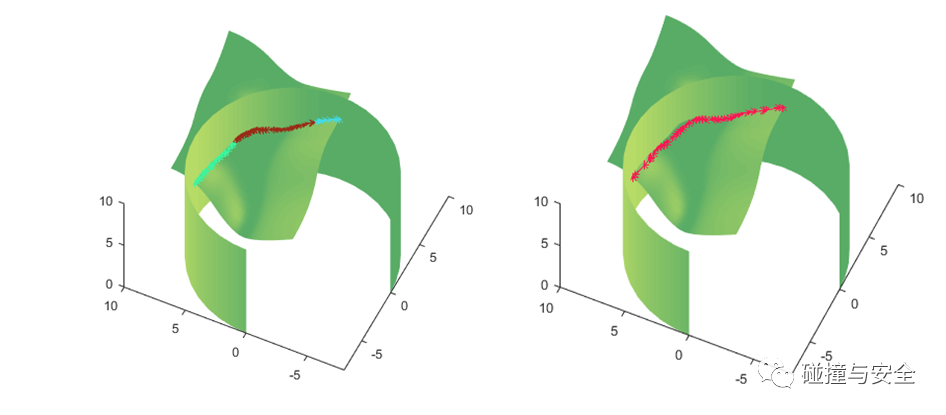
（两个参数曲面求交，很容易导致交点漏求、多求、求错的情况）


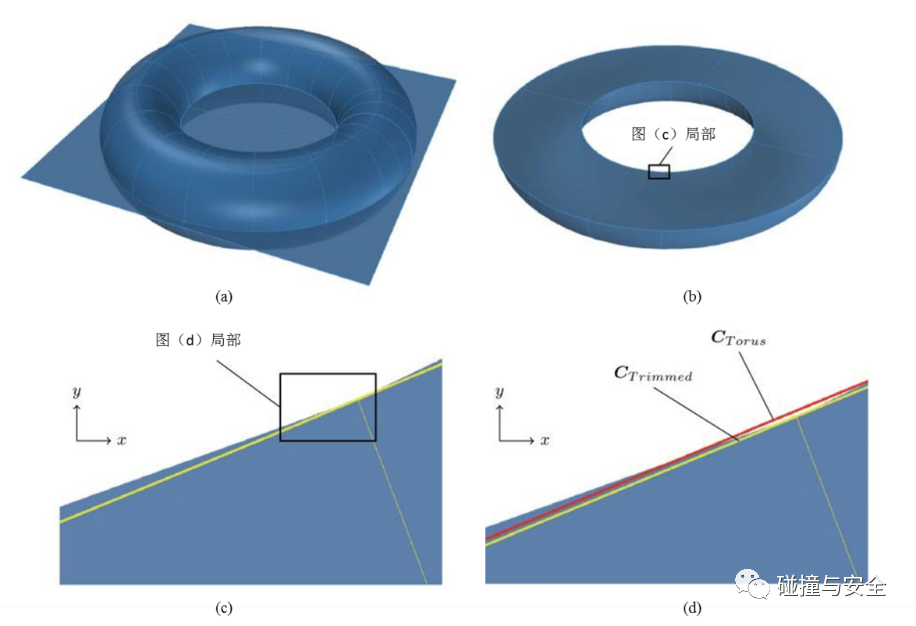
（曲面求交表面上看令人满意，然而放大局部会发现有缝隙（gap）或重叠（overlay）这种现实物体不可能发生的问题，这会导致难以构造IGA单元）

外行人乍一看觉得，不就是两张曲面交在一起，求出它们的交线不就行了嘛？问题在于，怎么求，或者说怎么又快又准的求出。当前IGA仅能对比较简单的形状进行模拟，对于复杂型面，尤其是通过曲面求交得到的裁剪曲面，要构造IGA单元并不是那么容易。



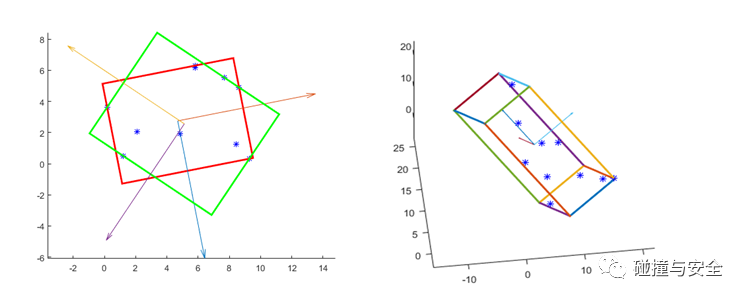
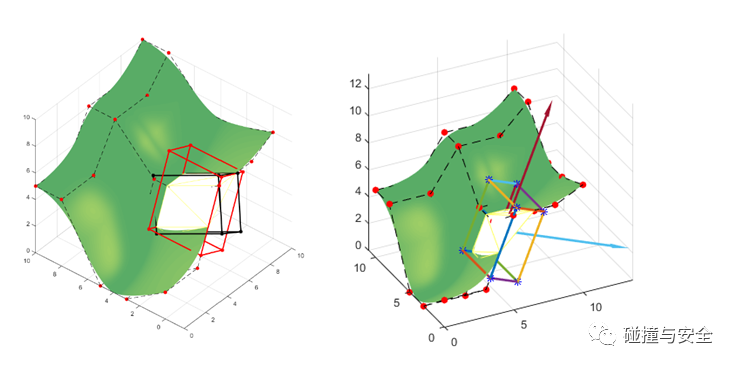
（曲面求交涉及的知识和要解决的问题非常繁杂，图示所列的是基于包围盒和碰撞检测算法求交，其中的碰撞检测类似于LS-DYNA中的接触算法，都是现在大火的人工智能、图像识别技术常用的方法）


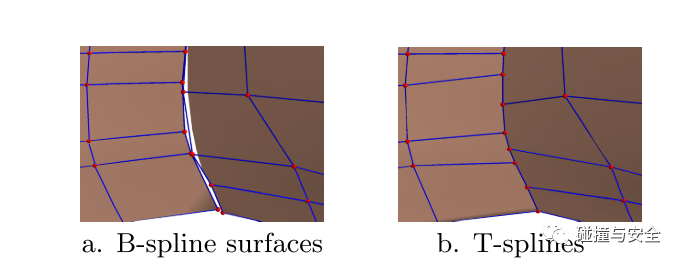
（为了解决传统IGA的B样条基函数出现缝隙问题，有学者提出利用T样条代替B样条作为基函数，图引自Sederberg T W, Zheng J, Bakenov A, et al. T-splines and T-NURCCs）

由于NURBS基函数是有理多项式，不像FEM形函数那样满足正交条件和插值特性，因此其边界条件施加远不如FEM方便（FEM只需对网格节点施加位移边界添加即可）。如果模型的边界是通过求交裁剪得到的不规则曲线，则更为困难。除此之外，尽管IGA单元具有数量少的优势，但由于其高阶特性，同等规模下IGA的计算效率并不比FEM高出多少，而工程上FEM的计算精度也完全满足要求，没必要刻意追求更高精度，因此IGA在实际工程应用上还有一段路要走。


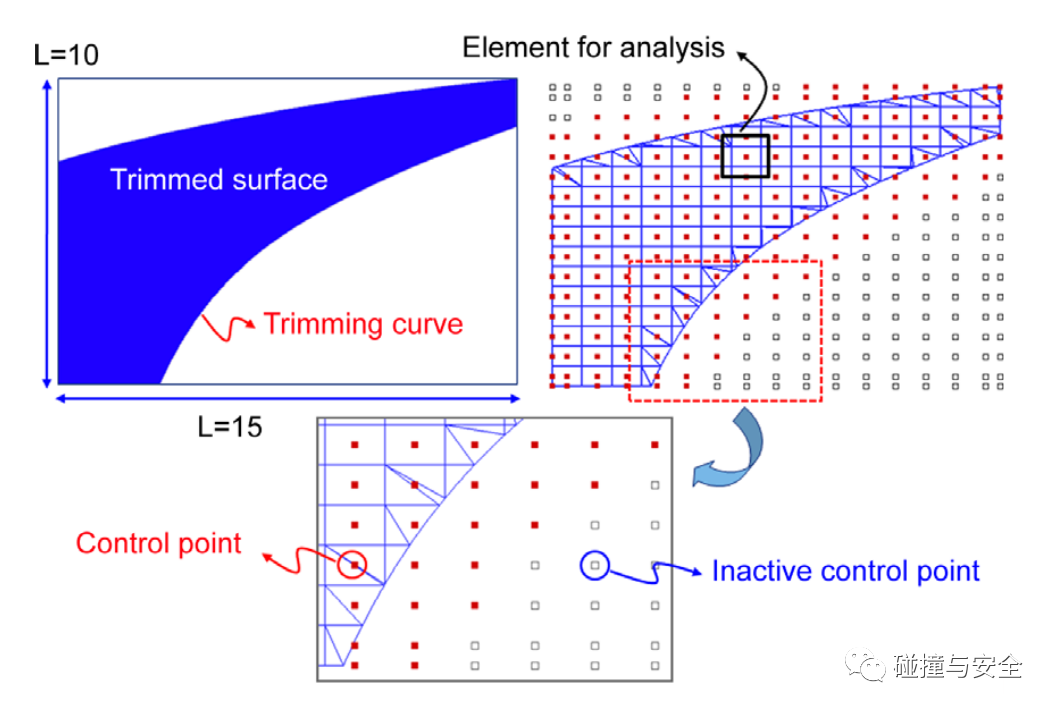
（裁剪边界的IGA单元构造）

无论如何，IGA自诞生以来，仅仅经过十几年时间的发展，便大有取代FEM之势，尽管当前工程上的主流分析方法仍然是FEM。随着IGA相关理论的完善和诸多问题（如裁剪曲面的单元构造、边界条件施加、计算效率问题等）的解决，相信会有越来越多的软件乐意将这一新的分析方法集成进去（当前ANSYS、Altair、DYNA已经将IGA集成到软件中了），并在更多领域开展应用。未来的CAE仿真领域，IGA势必能和FEM分一杯羹，或两者耦合分析发挥最大效能——毕竟，不用前处理就能直接分析的模型，有哪个工程师不爱呢？

05  题外话：国产CAE软件开发之路

无论是IGA方法还是FEM方法，现如今都被集成到各种各样工业软件中广泛应用于航空航天、船舶工程、汽车研发制造、家具家电、医药器材等工程领域，然而从事相关行业的工程师或学者会发现，当前主流的工业软件几乎清一色被国外公司垄断（DYNA/ANSYS/ABAQUS/NASTRAN/ADINA等），笔者曾经做过一定的国产CAD/CAE软件研发工作，结合自己的研发体会，在本文最后介绍下国产CAE软件的坎坷历程。

第一，很多人有个错觉，认为工业软件和我们生活中常用的app（微信、美团、王者荣耀等）并无二致，这好比是把一辆汽车的含量和一件衬衫相比。工业软件的本质和内核，从来就不属于IT产品，举个例子，现在比较热门的机器学习、图像识别、语音识别、大数据，其内核全部属于工业软件。工业软件最终呈现在我们面前的只是一个经过渲染和图形处理的集成平台的前端接口，它底层所含有的架构、数据结构、算法、逻辑，凝聚了各行各业最前沿的基础理论研究成果，包括但不限于计算机图形学、几何学、固体力学、流体力学、电磁学、热力学、声学、振动学、光学……，这意味着一个工业软件的开发，是背后各行各业团队高度合作的成果，当各领域最前沿的知识固化到一行行代码中，才能真正体现其应用价值、真正实现知识的代际传承。世界上最大的软件公司不是微软、不是谷歌、不是苹果，而是世界上最大的军火商洛克希德公司，多少年来其一直致力于工业软件的研发和更新

第二，我国工业软件研发之路充满了坎坷和无奈。初始，我们也是从模仿国外软件研发开始起步（最开始主要集中在二维CAD制图领域）。七五规划到十五规划的20年间，在国家机械部、国家科委的扶持下，国产工业软件（CAD/CAE）开发迎来了一波蜜月期，期间涌现出一批以唐荣锡、钟万勰院士等为代表的先锋人物，并开发出以北航（熊猫CAD）、大连理工（JIFEX）、中科院（飞箭）、中航工业（HAJIF）等为代表的一批优秀国产软件；然而，十二五规划之后，中国开始两化融合，科技部不再分管这方面工作，而工信部认为工业软件研发并不属于基础科研领域，不予资助，工业软件研发从此变成了“爹不疼娘不爱”的野孩子。什么概念呢？以全球最大的仿真软件开发商ANSYS为例，据统计，其每年在软件研发投入上达20亿人民币；而我国在十五规划到十二五规划的15年期间，对工业软件研发的总投入不足2亿人民币。这意味着国外一家厂商1年的研发费用投入吊打我们整个国家15年总投入的10倍，更遑论研发团队和高精尖人才的投入。

第三，工业软件的研发只是起步工作，更重要的是后续一系列更新迭代。工业软件诞生的一般流程是“工程需求——理论研究——软件研发——工程试用和反馈——商业化——市场推广——更新迭代”。软件开发难度自然不言而喻，但若没有一个良好的生态循环保证，其最终的下场就是被淘汰或并购。近十几年来，国外各大软件供应商针对基础理论和技术的更新拓展竞争达到了水深火热的地步，各大厂商疯狂并购、重组，其间每一次的技术整合都带来软件的进化——无论是人机交互还是底层算法。国外软件起步早，早期打入我国市场后并不注重盗版打击，一方面是由于我国知识产权保护法不完善，另一方面有一定的刻意成分，因为借助正版或盗版软件的广泛传播使用，厂商不但省去了宣传推广成本，还能及时收集软件使用中的问题，最终的目的只有一个——使自家软件不断迭代更新、不断提升产品竞争力。相较而言，我国普遍在整个生命周期的第一步“工程需求”就折戟沉沙，试想一下：作为企业人员，与其自己花几十年搞一套程序出来（搞出来的程序还未必比得过人家，还要后面花几十年的时间进行维护），花费几十万购买国外软件的现成使用权他不香吗？作为高校院所，铁打的支撑流水的学者，与其花费大量精力搞一套国产自主软件，直接用破解版的国外软件算出自己想要的结果，不是更快更准？毕竟，论文、毕业、评职称才是现在的王道啊。

总之，我国工业软件迟迟发展不起来，其中固然和国外软件以摧枯拉朽的势头长驱直入有关，然而国家不重点扶持、缺少人才和资金的投入，软件本身研发难度大、周期长、收益慢，当前资本市场和实际应用无价值导向，这其中一系列原因，都是制约国产软件的瓶颈。工业软件在现代工业的重要地位不言而喻——我们总把汽车比喻为现代工业的皇冠，将发动机和芯片比喻为皇冠上的明珠，然而，工业软件才是实现皇冠和明珠从无到有的关键工具。

德国率先喊出智能制造和工业4.0，引起全世界国家的高潮，各大企业纷纷高喊数字化转型，让软件贯穿设计、研发、制造、管理、运营、维护、反馈各领域，相应也带动了资本市场关于半导体、人工智能、芯片等行业的一波红利。却没人愿意承认，我国至今都没有一款真正达到世界先进水平的工业软件，我们针对数字化和智能制造浪潮所做的所有努力，都必须基于国外软件这一基本工具；谁又能想到，一旦从工业软件上卡脖子，一旦停止对工业软件的使用权，以上所有的行业前景不过是纸上谈兵而已。

06  参考文献

1.Breitenberger M, Apostolatos A, Philipp B, et al. Analysis in computer aided design: Nonlinear isogeometric B-Rep analysis of shell structures[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 284: 401-457.

2.Rank E, Ruess M, Kollmannsberger S, et al. Geometric modeling, isogeometric analysis and the finite cell method[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 249-252: 104-115.

3.Marussig B, Hughes T J R. A Review of Trimming in Isogeometric Analysis: Challenges, Data Exchange and Simulation Aspects[J]. Archives of Computational Methods in Engineering, 2017.

4.Kim H J, Seo Y D, Youn S K. Isogeometric analysis with trimming technique for problems of arbitrary complex topology[J]. Computer Methods in Applied Mechanics & Engineering, 2010, 199(45): 2796-2812.

5.Kim H J, Seo Y D, Youn S K. Isogeometric analysis for trimmed CAD surfaces[J]. Computer Methods in Applied Mechanics & Engineering, 2009, 198(37): 2982-2995. Piegl L A, Tiller W. Geometry-based triangulation of trimmed NURBS surfaces[J]. Computer-Aided Design, 1998, 30(1): 11-18.

6.Sederberg T W, Zheng J, Bakenov A, et al. T-splines and T-NURCCs

7. Lespiegl, Waynetiller. 非均匀有理B样条[M]. 清华大学出版社, 2010.

8. 施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 高等教育出版社, 2001.

9. 朱心雄等. 自由曲线曲面造型技术[M]. 科学出版社, 2000.

10. 孙家广. 计算机图形学(第三版)[M]. 清华大学出版社, 1998.

11. 邢誉峰. 计算固体力学原理与方法[M].

12. 林雪萍. 工业软件黎明静悄悄.

13. 苏楠. 工业软件是制造强国之重器.