电动赛车半主动悬架系统仿真及实现

摘要：应用汽车动力学理论，以1/2汽车悬架模型为研究对象，用调节减振器的阻尼系数法，建立了二自由度电动赛车的半主动悬架最优控制模型，利用编制的路面谱作为激励输入进行了仿真，并与被动悬架性能进行了对比。结果表明，半主动悬架在车身垂直振动加速度、悬架动行程、轮胎形变量的改善度分别为31.3%、21.4%、12.6%，使车身的振动被控制在某个范围之内，大大提高电动赛车在行驶过程中的平顺性。

作者信息：
姓名：潘军号，赵海军，李一凡，姜蕴珊，徐征，王志强
单位：天津职业技术师范大学汽车与交通学院；天津动核芯科技有限公司

作者简介：赵海军，博士，副教授，硕士研究生导师，研究方向为车辆振动噪声控制、汽车动力学、排放控制。

基金项目：天津市高等学校大学生创新训练计划项目(201910066054，201910066082)、国家自然科学基金资助项目(U1604141)、新开普教育部产学合作协同育人项目（201801097003）资助。

前  言

电动赛车是当代大学生创新训练研究的主要对象，其操控性、制动性等性能分析和车身、车架、悬架等的设计可以很好地作为大学生的研究方向。悬架是现代汽车上的重要总成之一，其主要任务是传递作用在车轮和车架或车身之间的一切力和力矩，且缓和路面传给车架或车身的冲击载荷，衰减由此引起的承载系统的震动，保证汽车的行驶平顺性，保证车轮在路面不平和载荷变化时有理想的运动特性，保证汽车的操控稳定性。半主动悬架是一种可控悬架，可以不改变悬架刚度而只改变悬架阻尼来实现对悬架性能的调节，结构相对简单，成本低廉，性能优良，有广泛的应用前景。解雅雯利用电磁阀改变节流阀的流通截面面积的大小，进而控制节流阀进出油液量，以把减振器阻尼进行多级分段调节。赵强等引入惯容器替代中间质量实现双磁流变阻尼器的双层半主动隔振，建立系统动力学模型，设计基于模型的控制方法，采用具有全局收敛性能的自由搜索算法进行结构参数和控制器参数的联合优化，并建立数值模型及用复合激励对优化所得方案进行测试和验证。相对于传统悬架系统，电动赛车的半主动悬架系统可以对车身行驶稳定性加强，可以使电动赛车车身的振动被控制在某个范围之内，大大提高电动赛车在行驶过程中的平顺性，从而在比赛中取得更好成绩。

本文建立电动赛车二自由度的半主动悬架模型和综合性能目标函数，输入参数，获得悬挂质量垂直振动加速度、悬架动行程、轮胎动变形的输出，建立MATLAB/Simulink仿真模型，通过路面激励输入进行仿真，对悬挂质量垂直振动加速度、悬架动行程、轮胎动变形仿真结果与被动控制进行对比。

1 二自由度半主动悬架模型的建立

1.1 二自由度悬架动力学模型

1/4车辆模型经常用于悬架系统的分析和设计。传统被动悬架可以简化为具有弹簧和阻尼器的双质量二自由度振动系统，如图1a所示。在电动赛车的半主动悬架模型中保留了弹簧，用以支撑静载悬挂质量，阻尼器由一个力发生器u代替，如图1b所示。


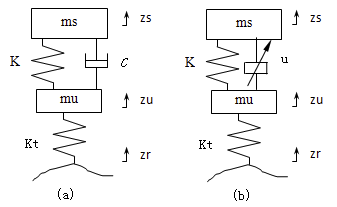
图1 电动赛车的1/4动力学模型

该模型对系统作了如下假设：

（1）悬挂质量与非悬挂质量均为刚体；

（2）悬架系统具有线性刚度和阻尼；

（3）悬架在工作过程中不与缓冲块碰撞；

（4）轮胎具有线性刚度，且在汽车行驶过程中终与地面接触。

1.2 系统状态空间的建立

令ms为簧载质量，mu为簧下质量，Ks悬架刚度，Cs阻尼系数，zs，zu,zr分别为悬挂质量位移、非悬挂质量位移和路面激励。

根据牛顿第二定律，建立动力学方程：

               (1)

                      (2)

选取悬挂质量位移zs和振动速度，非悬挂质量位移和振动速度为状态变量，令，状态向量为，则系统状态方程为：

                   (3)

其中：



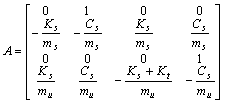
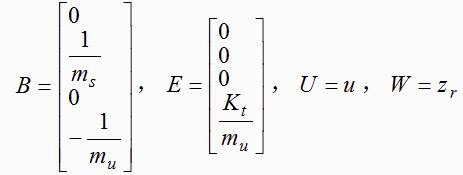
半主动悬架最优控制目标是提高汽车平顺性和操纵稳定性，反映在物理量上就要尽可能地减小悬挂质量垂直振动加速度和轮胎变形量，并限制悬架动扰度，同时从实现控制的角度看，应使控制能量的消耗较小。为减小执行元件所需的功率，主要采用调节减振器的阻尼系数法，只需提供调节控制阀、控制器和反馈调节器所消耗的较小功率。因此，综合性能目标函数可确定为如下形式：

                    (4)

根据状态方程，向量Y的表达式为：

                        (5)

其中：





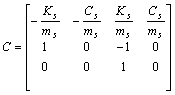
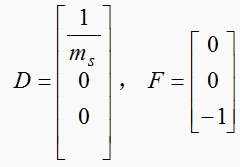
性能指标函数可以写为：

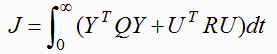                      (6)


式中：

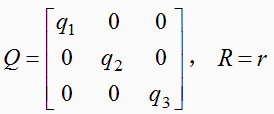
2 动态性能仿真分析

根据已经建立的半主动悬架动力学模型，结合提出的最优控制策略，在MATLAB/Simulink软件中，先建立二自由度1/4电动赛车悬架模型和最优控制的半主动悬架模型，生成随机路面垂直位移参数并输入系统，然后，半主动悬架根据最优控制策略计算最优积分值，最后输出半主动悬架和被动悬架性能仿真对比。

2.1 路面谱的施加和仿真模型的建立

从功率谱密度获得路面激励时域模型，也就是随机路面不平度,通用的方法是将路面不平度定性为平稳的Gaussian随机过程。对于平稳Gaussian随机过程,有多种方法可以生成路面不平度时域模型。其中主要的方法有：滤波白噪声生成法，基于有理函数PSD模型的离散时间随机序列生成法，根据随机信号的分解性质所推演的频谱表示法，以及基于幂函数功率谱的快速Fourier反变换生成法等。其中谐波叠加法是将路面不平度表示成大量具有随机相位的正弦或余弦之和，算法简单，易于程序实现，迭代出的路谱有一定精度。因此，选用此方法编写生成路面谱的软件。由于MTALAB语言具有强大的数据计算能力，故选用MATLAB作为路谱软件的开发工具和平台。基于上文描述的谐波叠加算法，开发了路面谱生成软件,输入计算参数主要包括车速和路面不平度系数、时间频率下限、时间频率上限、路谱最大时间、空间主频下限、空间主频上限、生成路谱条数、时间频率间隔，输入这些参数后，通过计算就可以生成路谱文件，生成的路面不平度时间历程如图2所示。


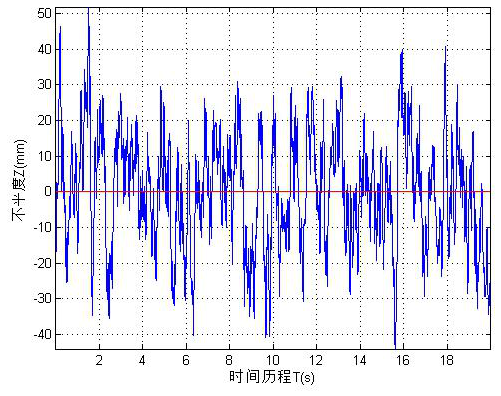
图2 路面激励(路面不平度曲线)

有了路面激励信息的具体数据，就可以在MATLAB/Simulink建立半主动悬架的仿真模型。在该模型中，为了和被动悬架的振动加速度、悬架动行程、轮胎变形进行对比，施加了三个显示器（scope）模块，这样仿真完成后，就可以通过这三个显示直接看对比结果。同时，为了认识半主动悬架与被动悬架的弹簧速度、簧载质量与路面激励位移之差的对比，增加了两个显示器模块，为了监测半主动悬架控制力变化情况，增加了一个显示器模块，一共六个显示器模块，所建模型如图3所示。


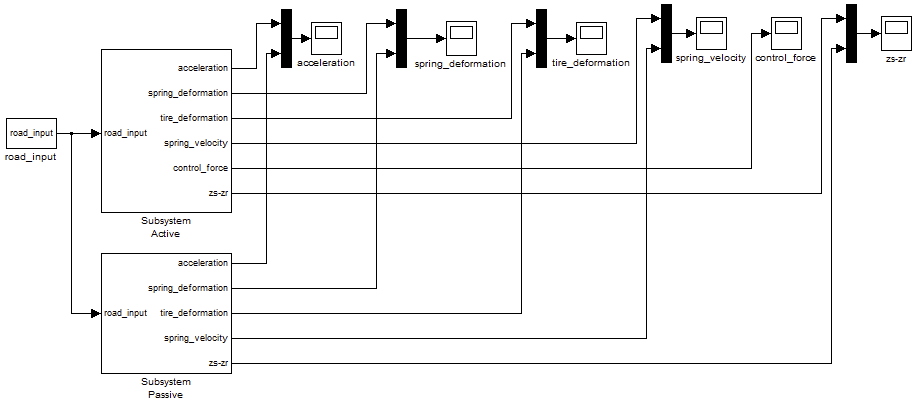
图3 仿真模型

仿真模型选取1/4汽车悬架主要参数，如表1所示，利用图3所建仿真模型，导入路面激励，就可以仿真。

表1 悬架主要参数


2.2 仿真分析与对比

经过仿真，电动赛车半主动悬架和被动悬架的车身垂直振动加速度、悬架动行程、轮胎变形0-10秒内时间历程的仿真结果对比分别如图4、图5、图6所示。从图中可以看到，半主动悬架的车身垂直振动加速度比主动悬架的幅值普遍小了很多，半主动悬架的悬架动行程比主动悬架的幅值小了一些，半主动悬架的轮胎变形比主动悬架的幅值也小。


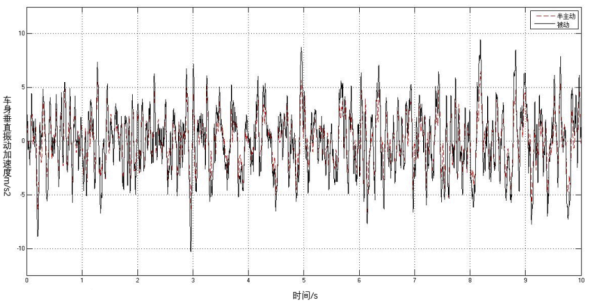
图4 车身垂直加速度时间历程


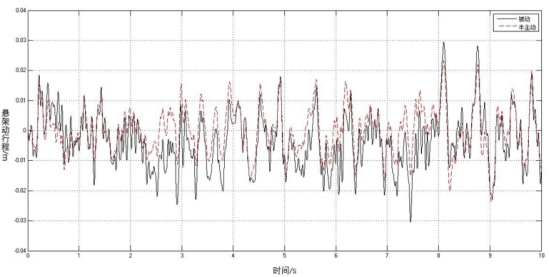
图5 悬架东行程时间历程


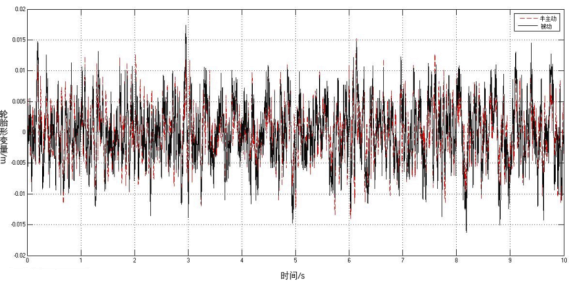
图6 轮胎变形量时间历程

为了进一步详细对比，在图4、图5、图6中分别选取车身垂直振动加速度、悬架动行程、轮胎变形时间历程中幅值最大进行对比，结果如表2所示。从表中可以看出，在被动悬架控制下，车身垂直振动加速度的9.4316 m/s²，采用半主动控制后车身垂直振动加速度6.4811 m/s²，改善度提高了31.3%；在被动悬架控制下，悬架动行程的0.0295 m，采用半主动控制后悬架动行程的0.0232m，改善度提高了21.4%；在被动悬架控制下，轮胎形变量的0.0174 m，采用半主动控制后轮胎形变量的0.0152m，改善度提高了12.6%。

表2 悬架振动特性对比


从以上对比数据可看出，电动赛车半主动悬架在运行中的车身垂直振动加速度、悬架动行程、轮胎形变量的峰值相对于传统的被动悬架来说有明显的下降，说明半主动悬架相比于传统的被动悬架能更好的提升电动赛车行驶的平顺性和操纵稳定性。

3 结论

（1）建立了二自由度1/4电动赛车半主动悬架动力学模型，建立了电动赛车被动悬架和基于最优控制的半主动悬架的MATLAB/simulink仿真模型；

（2）利用编制的路面谱作为激励输入进行了仿真，与被动悬架相比，半主动悬架在车身垂直振动加速度、悬架动行程、轮胎形变量的改善度分别为31.3%、21.4%、12.6%。