基于非线性模型预测控制的协同轮胎力避障方法研究

编者按：随着自动驾驶技术的不断发展，自动驾驶汽车需要处理的工况也越来越复杂。在极端场景下（如湿滑路面)，车辆在转弯时往往会产生大的侧滑角，严重时甚至会发生甩尾，容易造成事故伤亡，因此，自动驾驶汽车应具有处理高侧滑角不稳定情况的能力。通过模仿专业驾驶员的漂移操作可以为解决车辆的高侧滑角失稳提供一种思路。与非专业驾驶员和常规控制系统不同，专业驾驶员可以在保持高侧滑角的同时稳定车辆，甚至可以操纵汽车按自己的意图行驶。因此，通过研究漂移的动力学机理以及专业驾驶员实现漂移操作的方法，建立合适的控制器使自动驾驶车辆在高侧滑角下仍能保持稳定性和操纵能力，这将有助于减少因车辆甩尾带来的事故伤亡。


本文译自：

《Coordinating Tire Forces to Avoid Obstacles Using Nonlinear ModelPredictive Control》

文章来源：

IEEE Transactions on Intelligent Vehicles

作者：

Matthew Brown and J. Christian Gerdes

原文链接：

https://ieeexplore.ieee.org/abstract/document/8910387


摘要：为了安全地在高动态场景中行驶，自动驾驶汽车必须对环境的改变作出快速反应，并且在轮胎处于附着极限时可以合理地分配轮胎横纵向力。本文设计了一种能够处理上述复杂工况的非线性模型预测控制器并进行实验验证。通过仔细选择车辆模型和车辆及障碍物之间的数学表达，本文能够在保证车辆运动模型的准确性及其与障碍物保持安全距离的情况下使控制器实现快速计算求解。测试车辆通过变换车道躲避两个突然出现障碍物，该实验证实了所提出控制器在危险工况下轮胎力处于附着极限时能够协调轮胎的横纵向力。

关键词：自动驾驶汽车，车辆动力学，避障，非线性模型预测控制

1 引言

随着自动驾驶汽车的快速发展，自动驾驶汽车需要处理大量现实世界场景。为了在复杂的城市环境中保证车辆和其他交通参与者的安全，即使在低车速和加速度的情况下，仍有许多具有挑战性的问题需要克服。此外，自动驾驶汽车还必须能够处理高车速和加速度下的动态工况。特别地，自动驾驶汽车还应实施突发和极端行为以避免与其他车辆或目标发生碰撞。在紧急工况下，应充分利用车辆的潜力以避免碰撞发生。

通过将运动规划的预测能力与实时控制的速度和鲁棒性相结合，模型预测控制（MPC）已成为一种流行的技术。MPC能够使车辆在变化的环境下快速作出反应，同时确保现在采取的行动不会在未来将车辆置于危险状态。在每个采样时刻，模型预测控制器通过求解最优化问题计算得到状态和输入序列。然后将第一个输入量（或者某个初始输入序列）作用于系统并在下一个采样时刻重复这个过程。MPC控制器通常被定义为跟踪控制器，其目标是在保证如输入饱和和避免碰撞等约束时遵循期望的状态轨迹(由上层规划或决策得到)。这些控制器代表了关于动态模型，障碍表示和在模型保真度，最优性及计算时间之间适当权衡的数值近似方法的设计决策集合。

线性或线性时变的MPC已经被证明是强调快速求解下的车辆控制的一种十分有效的方法。通过解决基于线性动力学模型的凸优化问题，控制器可以快速找到近似问题的全局最优解。Falcone[1]等人展示了线性MPC作为冰面高速行驶工况下轨迹跟踪器的有效性，同时在附加约束下保证了车辆的横摆稳定性[2]。相似地，Brown [3]和Funke[4]等人通过约束速度在状态空间的安全区域内，这是由Beal和Gerdes[5]定义的，来确保车辆在干燥沥青路面上的横摆稳定性。模型的预测能力对于这些任务是至关重要的，这确保了当下的输入能够稳定车辆而不会影响其未来的性能。使用线性模型能够快速实现稳定，但是这也限制了控制器能力的发挥。特别地，车辆横纵向动力学以非线性方式耦合，这使得线性MPC同时规划横向和纵向输入是时遇到挑战。这在轮胎处于摩擦极限时尤为明显，并且系统非线性更强并且难以用线性模型近似。

另一种方法是使用非线性车辆模型并解决一个非线性最优化问题。这需要牺牲凸优化的全局最优性和收敛性来换取额外的建模能力。Falcone等人[1]使用非线性MPC（NMPC）计算了双移线实验中用于跟踪路径的方向盘转角，并且分析了制动力如何影响问题的复杂性[6]。他们提出一种控制器来模拟每个轮胎上的合力，但是指出模型的复杂性限制了控制器的实时实现。Liu[7]和Febbo[8]等人研究了避障任务，每0.5s规划一次参考速度曲线。虽然这些算法在复杂环境下使用非线性模型，但是较长的求解时间限制了算法对环境变化的快速反应能力。尽管存在上述挑战，非线性模型仍然具有吸引力，因为其能够捕获轮胎横纵向力的耦合关系。

其他学者研究了克服NMPC求解时间过长的方法。Gao等人[9]将直接求解转向和制动指令的方法与分层方法进行比较，分层方法首先利用低保真度模型找到无障碍路径，然后在求解转向和制动指令。他们特别指出，将避障和车辆控制集成在可以实时运行的单一控制器中是具有挑战的。Frasch等人利用实时迭代的方法研究NMPC的计算时间问题，给出了结构化环境下车辆在低附路面上避障的仿真结果[10]。本文选择在输入使用之前能够完全收敛的单级控制器，并通过选择积分器、变量和重规划策略来减少NMPC的求解时间。

避障任务的关键设计是车辆和障碍物的表示。横向位置的简单边界易于快速求解，但在建模车辆的转弯运动时受到限制，并且与纵向位置耦合[3],[10]。其他明确考虑到障碍物的距离的方法不受上述缺点的影响，但是需要更长的时间来求解。常用的方法是用多面体集合来表示车辆（或机器人）与障碍物，并将这些几何之间的距离合并到目标或者约束中去[9],[11],[12]。虽然距离函数通常是不可微分的，但是可以采用合理的启发式方法来解决这个问题。Gerdts等人[13]采用不同的方法，将机器人和障碍物建模为凸多面体的并集，并调用Farkas引理将机器人和障碍物不重叠的约束转化为可处理的数值优化。Zhang等人[14]扩展了这一思想，将符号距离的概念包括在内，从而能够计算最小穿透轨迹。该方法允许将机器人和障碍物建模为多面体，避免了无法可微的有符号距离函数，但也引入了额外的变量和约束。因为这些内容必须添加到每个求解过程，因此它们会导致求解时间的显著增加。本文用一组圆来表示车辆，类似于Zieglar等人[12]的方法，并通过用另一组圆来表示障碍物来扩展这个方法。这种表示方法可以快速计算车辆与障碍物之间有符号距离函数的值和梯度，并且通过使用多个圆仍然可以捕捉车辆转弯的重要特征。

在紧急情况下，控制器需要迅速工作，充分了解轮胎横向力和纵向力之间的必要权衡，并使用可以表征车辆转弯的车辆和障碍物表示法。实现这一点所需的设计决策，特别是在试验车辆上，是本文的贡献。本文提出了一个NMPC控制器来计算车辆转向角和前后轮纵向力。采用单轨动力学模型和刷子轮胎模型建立车辆动力学模型，同时考虑稳态时纵向质量的转移和由纵向力所引起的横向力变化。避障通过一种新颖的表示方法进行处理，该方法将车辆和障碍物用一组圆表示，并计算所有车辆和障碍物圆对之间的有符号距离。通过选择总的纵向力和制动偏差作为优化变量，减少了待求问题的复杂性，同时仍使控制器能够在前后轴之间任意控制制动力。所建立的公式使得控制器能够足够快地实时运行，每50毫秒重新规划一次，并且足够复杂地在车辆极限下工作，在一个或多个轮胎完全饱和的情况下协调横向和纵向力。第二节描述了所选择的车辆模型，第三节解释了车辆和障碍物的表示，第四节描述了优化问题的表述。第五节比较了使用不同车辆和障碍物表示时控制器的求解时间，并证明了控制器在全尺寸车辆上的有效性，通过一个足够极端的工况证明所选模型的复杂性。在实验结果中，两个障碍物“弹出”到车辆前面，迫使车辆执行紧急车道切换。控制器协调各轴的制动力和转向力，同时成功避开障碍物。

2 车辆模型

车辆运动可以通过平面单轨模型进行预测，轮胎力来自单个摩擦系数下的刷子模型。

A.曲线坐标系

车辆位置相对于参考线表示。假设这条线具有连续的曲率，可以通过积分来计算车辆相对于参考线的航向和位置。虽然这条线可以定义任意的坐标系，但在本文中假设这条线对应于道路的中心线。车辆位置由相对航向，纵向位置s和横向位置e参数化表示。

B.动力学方程

单轨自行车模型的示意图如图1所示。


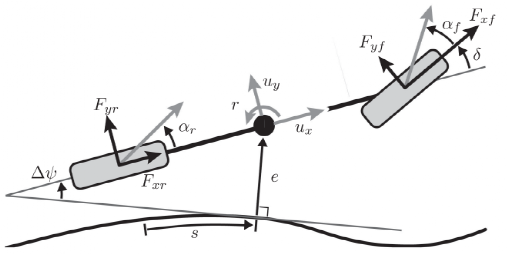
图1 曲线坐标系下的单轨车辆模型

车辆的速度变量是横摆角速度r和质心处横纵向速度ux和uy。

本文感兴趣的是明确地模拟每个轴上的横向和纵向力，车辆前后轮的横纵向力方程如下：



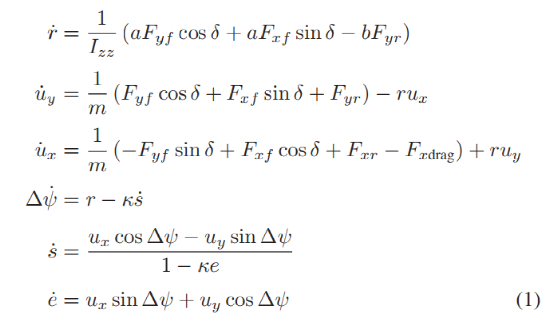
本文使用适用于低速的简单阻力模型。在不改变问题结构的情况下，该模型可以包括高速度下的空气动力学效应。

C.轮胎模型

前后轮胎上的横向力用轮胎刷子模型近似。该模型表征了侧向力与侧偏角α，轮胎方向与其速度矢量之间夹角的函数关系。计算公式如下：



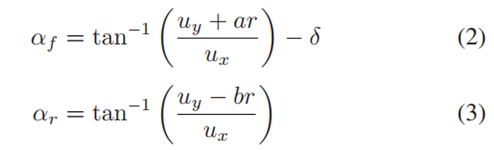
虽然使用组合滑移模型能够捕捉轮胎纵向力与横向力之间的相互作用关系，但是过快的轮速动力学会使处理纵向滑移变得困难。因此，本文利用摩擦圆（如Hindiyeh[15]所示，源自Pacejka[16]）用最大侧向力Fy来近似组合滑移刷子模型，侧向力的最大值由给定的纵向力和摩擦圆决定。因此，侧向力是侧向滑移角α、纵向力Fx(假定是输入)、法向载荷Fz以及侧偏刚度Cα和路面附着系数μ的函数。



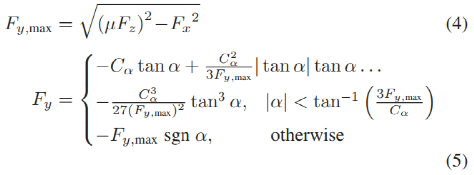
轮胎参数通过斜坡响应确定，其中车辆以恒定的速度ux行驶，δ以固定的速率缓慢增长，辨识结果如图2所示。


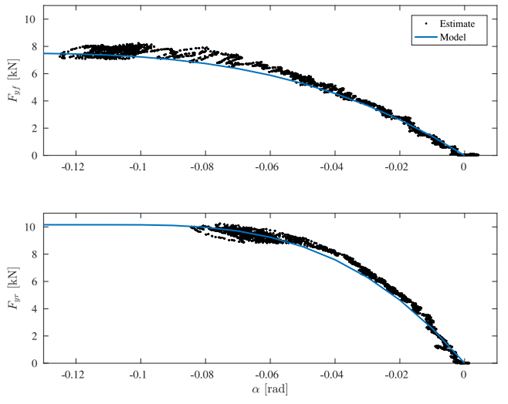
图2 轮胎模型辨识结果

利用测量的r、ux和uy，用(2)和(3)计算测试滑移角。通过测量的r、ux、uy以及稳态假设，测试力用方程(1)进行估计。这形成了一个线性方程组，可以求解Fyf和Fyr。如图2所示，所建立的模型代表了左右轮胎的集成效应，与实验数据非常吻合。

D.质量转移

通过假设静态重量分布和在小转角下添加稳态纵向重量转移的影响，对前后轮胎上的法向力建模如下：



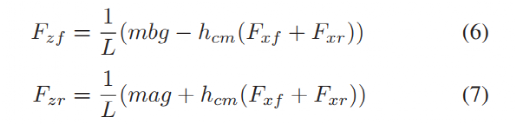
其中hcm是车辆质心离地高度。此处纵向重量转移模型等效于刚性悬架。虽然真正的汽车结构已经包含悬架，但是这种重量转移模型不会引入任何额外的状态，并在稳态下是准确的。关键的是，该模型可以表征制动时Fzf增加带来的影响，即提高了前轴横纵向力能够达到的极限值。此外，制动降低Fzr，从而降低了后轴横纵向力的极限值。横向重量转移没有明确的模型化，但在近似的单轨模型中，稳态效应被集中到轮胎模型中。

选取的车辆模型提供了状态变量和输入变量到状态导数的完整映射：



3 障碍物建模

所提出控制器的一个基本任务是避障，因此对车辆和障碍物的合理建模非常重要。在规划文献中，通常将车辆或机器人视为运动空间中的一个点 并在工作空间中进行路径规划[17]。通过这种方法，障碍物在更高的维度上被建模从而解决机器人的转弯、多关节等复杂运动。这对于基于采样的方法非常有效，在这种方法中，可以将障碍物碰撞视为黑盒并进行查询。然而，由于缺乏障碍物距离或有符号距离的解析表达式，使得在运动空间中使用数值优化方案进行规划具有挑战性。

另一种方法是将车辆视为位置空间中的一个点，并将障碍物放大至车辆尺寸。为了考虑车辆的转弯，障碍物可以进一步扩大[8]，或者可以根据运动空间内障碍物的线性化进行修正[18]。虽然这些近似方法更有利于数值优化，但它们往往会过度放大障碍物使得结果保守。

将车辆和障碍物建模为全维度比较困难，但可以更精确地处理它们的转弯运动。也许最直接的方法是对机器人和障碍物之间的有符号距离进行数值线性化，需要特别注意真实有符号距离不可微的情况[11]，[12]。另一种方法是假设将机器人用多面体或椭圆表示，并调用Farkas引理及其对偶条件代替避障约束[13]、[14]、[19]。这种约束是光滑的，可以通过增加变量和约束来进行数值优化，这将会大大增加问题的规模和求解时间。

车辆和障碍物的表示需要能够精确地反映车辆的大幅度转弯，同时应能保证足够简单的实时控制。为此，我们用一组共Nv个圆来表示车辆。每个车辆圆Vi（对于i=1…Nv）由半径和中心参数化，这取决于车辆的位置和航向。类似地，我们可以用一组共No个圆（用Oj表示）来表示任意障碍物。图3展示了用两个圆表示的车辆和用一个圆表示的障碍物。这种表示法可以快速计算任意车辆圆Vi和障碍物Oj之间的有符号距离d。如果所有的车辆-障碍物圆对之间的有符号距离均为正，则表示车辆和障碍物不相交，且不存在模型碰撞。


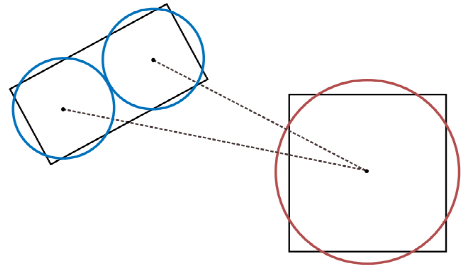
图3 车辆-障碍物表示方法

对于任意的两个圆C1和C2，分别由其在曲线坐标系中的位置和半径进行参数化，即（s1、e1、r1）和（s2、e2、r2），曲线坐标系中的有符号距离为:



当该距离为正时，表示C1和C2之间的真实距离。如果为负，则表示C1和C2之间的重叠距离。


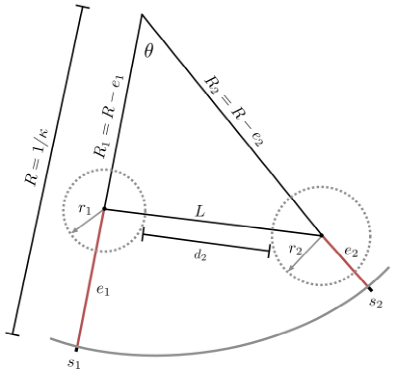
图4 笛卡尔坐标系下有符号距离

在曲线空间中，两个圆之间的有符号距离很容易计算，但在笛卡尔坐标空间中则不同。为了分析由曲率引起的（9）的近似误差，我们将其与笛卡尔坐标空间中的有符号距离进行比较，如图4所示。假设两个圆足够接近，参考线的曲率在它们之间保持，角度θ为。用余弦定理可以求出两个圆心L之间的距离：



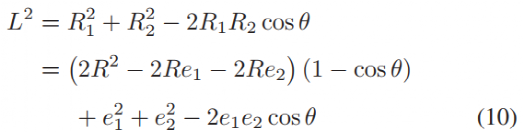
根据小角度假设，由，这在典型的道路曲率且两圆足够靠近时是合适的，从而取近似值。



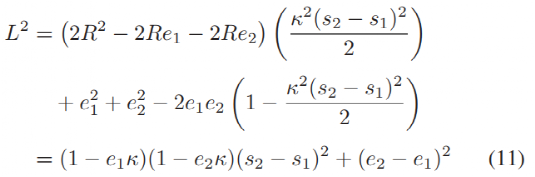
基于上边的假设，在笛卡尔坐标系下的有符号距离为：



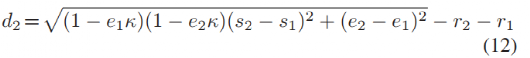
当曲率为零或两个圆同时位于参考线上时，两者之间的距离就是圆心距离d1，并且随着这些参数变化而平滑变化。虽然 d1 可表示有符号距离，但它会因因子的存在而与笛卡尔距离d2不同，当时距离估计偏大。尽管道路的曲率相对于道路的宽度通常非常小，但d2能够更准确地模拟距离，尤其是在高曲率道路上。

4 问题建立

控制器反复求解最优控制问题以计算的输入轨迹，以安全地引导车辆通过场景。它并不去决定应该通过每个障碍物的哪一侧以及以什么顺序通过或者车辆是否应该在某些障碍物之前停下来的组合问题。相反，控制器假设上层规划已经给出了一条驾驶通道，由所需的横向位置和速度轨迹决定。然而，本文强调，这些期望的轨迹可能非常粗略，仅用于向控制器展示它应该探索哪类解决方案。控制器有责任做出这个粗略的决定并计算一个安全且动态可行的完整状态轨迹。

A.离散化

最优化问题通过同步变换方法进行离散化。该方法考虑每个离散时间节点的状态和输入值，并使用数值积分方法将(8)中的微分方程转换为差分方程，这里假设采样步长内输入为常值。

选择一个足够复杂的积分器来准确地对运动方程进行积分是很重要的,但是它也应该相对简单以保证快速求解。一个非常常见的方案是欧拉方法，或前向欧拉法：



另一个方法是显式二阶的龙格库塔方法，该方法有时也被称为中点法。



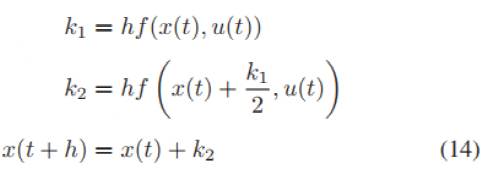
给定积分器的性能取决于时间步长 h和动力学模型。虽然该方法可以计算误差界限（如著名的四阶龙格库塔公式的总积累误差是），但是很难用微分方程的先验知识来决定可以接受的固定步长。

图5显示了对输入轨迹 以及给定车辆模型(8)与车辆状态r和e的不同积分器进行积分的结果。输入轨迹来自紧急车道变换，这代表激烈的车辆操作，因为状态导数幅值较大并且状态在相当长的时间内处于轮胎模型的饱和区域。步长为h=0.5 ms的欧拉方法作为基线，步长为 h = 50 ms 的欧拉方法非常不准确，而对于相同的步长，RK2 表现非常好。此外，对于此模型，RK2 的性能与 RK4 一样好，但计算量明显减少。由于这些原因，本文选择 RK2 作为离散化方法。


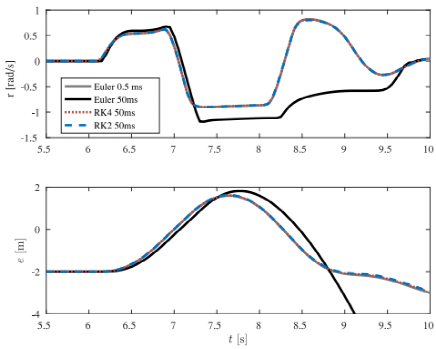
图5 不同离散方法的比较

B.变量转换
在优化问题中使用Fxf和Fxr作为纵向输入变量是合理的，但在给定问题下可能会有更好的选择。最小化或限制纵向加速度很重要，因此除了 Fxf和Fxr外，需要作为变量，每个阶段总共有四个纵向变量。此外，本文希望约束Fxf和Fxr具有相同的符号，以防止驱动电机和制动器同时工作。该约束公式如下：



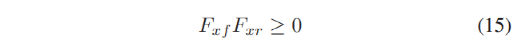
但是该约束中当Fxf=0且Fxr=0时是一个鞍点，这是输入空间中的典型位置。由于该约束的Hessian矩阵不是正定的，所以它导致优化问题的拉格朗日Hessian矩阵不是正定的。这破坏了牛顿法的前提，即需要正定的Hessian矩阵。因此，包含此约束不利于求解器的求解速度和稳定性。

另一种变量选择是总纵向力 Fx 和制动分配λbrake。制动分配表示应将总纵向力如何分配给前轴和后轴。给定Fx、λbrake和固定驱动分布λdrive，可以计算Fxf 和 Fxr：



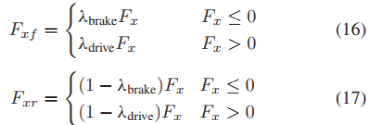
这种变量选择隐式约束了Fxf 和 Fxr具有相同的符号。此外，控制器可以通过将作为优化变量来最小化纵向冲击。由于制动系统可以比系统中的其他动力学更快地引导前后轴之间的力，所以我们不需要引入制动。在这个假设下，问题每个阶段只需要三个纵向变量：，比使用Fxf 和 Fxr的公式少一个。

C.代价函数

控制器的目标是粗略地跟踪期望的横向位置和纵向速度序列，同时找到一个可行的状态轨迹，避免太靠近或碰撞障碍物和道路边缘。成本函数是：



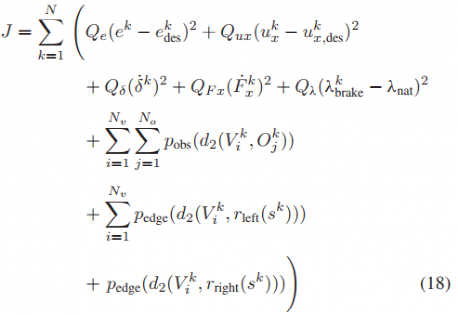
其中Qe 和 Qux 是横向位置误差和纵向速度误差的二次权重，Qδ和QFx是的二次权重，Qλ是一个小的二次权重，其使得λbrake接近由λnat表示的典型值。连续和可微的惩罚函数pobs 和 pedge在大于某个距离时为零，低于该距离则是一个二次函数，即



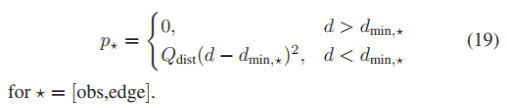
上式表明轨迹仅在车辆与障碍物距离dmin,obs或道路边缘距离dmin,edge（由 rleft(s)和 rright(s) 表示）时pobs 或 pedge才不为零。此时需要选择权值Qdist 来调整成本函数；如果路径上不发生碰撞，控制器将采用期望不同的横向位置和纵向速度。

(19)中的切换状态不是先验已知的，可以在求解器根据需要将计划的车辆状态移近或远离障碍物时来进行优化。控制器的一个隐含功能是确定车辆何时必须靠近某些障碍物附近以避免与其他障碍物发生直接碰撞，故该信息不会提前收到限制。虽然惩罚函数是分段定义的，但它是连续的，并且对于优化变量具有连续的一阶导数，这使其适合数值优化。

增加使用的圆圈数量（Nv，No）使控制器能够更准确地捕捉车辆或障碍物的形状，例如，在角落放置较小的圆圈以创建更接近矩形的表示。然而，这些更详细的表示是有代价的。虽然增加Nv和No不会增加优化变量或约束的数量，但评估(18)的计算成本随着增加。本文中使用 Nv= 2以表征车辆转弯运动；选择No=2，每个障碍物用一个圆表示。

D.非线性规划和求解

前文使用u来表示模型的输入，现在定义来表示成本函数中输入变量u的最高阶导数，并且我们定义来表示用δ和Fx增强的状态。对于本文所提出的问题，和。针对这些变量的非线性问题是：



其中fdis是车辆模型(8)与和之间的一阶关系，用 二阶龙格库塔积分器 (14) 进行离散。图片和 δ有上限和下限，Fx有上限，这些构成该问题的约束条件。

每个轮胎可用的力不是恒定的，其随着负载的变化而发生变化。一个轮胎的总力可以表示为，这是摩擦圆约束。横向轮胎模型强制执行此约束以限制给定纵向力下的横向力大小，但还需要约束纵向力。使用(17)计算的Fxf和Fxr都受到由（7）计算得到的和的限制。

用一个附加因子γ表示可作为纵向力的部分占总轮胎力的比例。如果γ = 1，则表示Fxf或Fxr可以使用所有的轮胎力，同时Fyf=0或Fyr=0。由于精确估计摩擦力受到限制，将Fxf和Fxr限制在稍低的γ值是有用的，这使得控制器可以给出最大的横向力。本文介绍的实验是在 γ = 0.95 的情况下进行的。

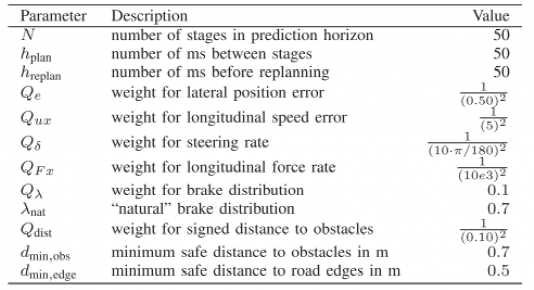
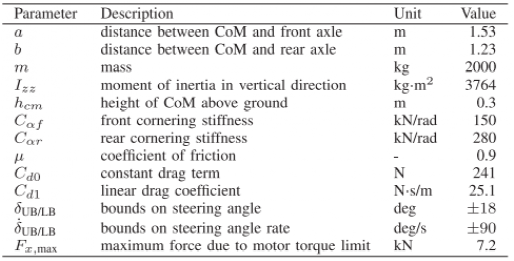
优化问题求解变量δ、Fx和λbrake，并通过 (17) 转换为δ、Fxf和 Fxr。然后将后者输入到下级控制器作为要跟踪的目标。优化问题的成本函数权重和其他参数如表I所示。该问题通过 FORCES NLP内点求解器[20]解决，使用来自 CasADi [21] 的成本函数和约束来实现自动微分。求解器使用 BFGS [22]逼近(20)的拉格朗日Hessian矩阵，并利用问题的稀疏性来提高求解时间。

表Ⅰ参数列表


E.重新规划

与二次（或其他凸）问题相比，非线性问题需要更多的计算时间。在高动态工况中，车辆状态会发生显着变化，因此考虑计算延迟很重要的。控制器使用的求解策略如图 6 所示。假设控制器已经有一个规划，或者完整的状态和输入轨迹，它会同时做两件事。首先，控制器通过将输入序列δ、Fxf 和Fxr作用于车辆，在接下来的 50 毫秒内执行该规划。测试车辆上的下级控制器每10毫秒接受一次新命令，因此每10毫秒根据当前规划进行线性插值以找到正确输入。这种线性插值与积分器的假设一致，即在当前是恒定的。其次，它使用该输入序列模拟车辆模型，以获得50毫秒后状态的估计，并根据模拟的初始状态开始计算下一时间步长的规划轨迹。


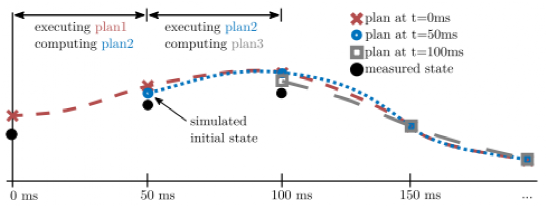
图6 控制器求解策略

规划轨迹依赖于其初始状态。模拟的初始状态永远不会与测量的初始状态完全匹配，但模型准确时两者应该是接近的。这使控制器能够规划出到达计算结束时均有效的轨迹，而不是仅在计算开始时有效的轨迹。

一种策略是复制最近一次的规划结果。尽管通常只使用规划输入的前50毫秒结果，但该方法使计算时间具有鲁棒性。如果求解器未能在50ms 的时间限制内收敛，控制器可以在计算下一规划时继续执行上一规划指令。这在下文的实验期间发生过一次。

F.限制

控制器的目标是可行域内中找到局部最优轨迹，而不是在可行域中做出决策。换句话说，控制器依靠上层决策来选择是通过右侧还是左侧的障碍物。在选定的可行域内，控制器解决一个非凸优化问题。所使用的内点法只能找到局部最优解，该方法缺少凸问题收敛的数学保证。然而，根据经验，求解器在多数条件均可收敛，所得解在仿真和实验中都有效地控制了车辆。

5 结果

A.仿真对比

用圆表示车辆和障碍物可以实现实时控制。为了证明这一点，将本文所提出的控制器与除了用矩形表示车辆和障碍物外其他条件相同的控制器进行比较。这种表示是准确的，没有近似值，但需要在车辆的每一侧和每个障碍物处增加附加变量。对于三个矩形而言，增加的12个变量用于两个额外的标量不等式约束和两个标量等式约束以强制车辆按无碰撞路径行驶，如 Zhang [14] 所述。

在仿真中，车辆以ux,des=14m/s的速度在直线道路上的右侧车道上行驶。前方一个障碍物挡住了右侧车道，之后15m处的第二个障碍物挡住了左侧车道。模拟中使用的圆形和矩形表示的比例描述如图3所示。两个控制器都成功地引导车辆通过车道变换操作避开障碍物。两个控制器产生相似的控制输入，但求解时间不同，如表II所示。

表Ⅱ 计算时间对比


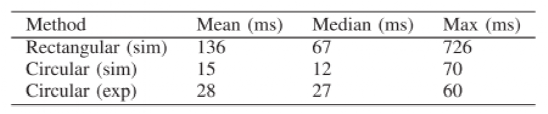
矩形（更一般地，多面体）表示允许非常精确地处理车辆和障碍物，但需要过多的计算时间以至于难以实时运行。圆形表示一种可接受的近似处理，其对于实时控制来说足够简单。

B.实验平台

实验平台采用使用学生制造的电动汽车X1。X1的模型参数如表Ⅲ所示。机载NovAtel SPAN-SE导航系统将全球导航卫星系统(GNSS)的测量结果与来自包含陀螺仪和加速度计惯性测量单元的测量结果相融合，以提供准确的车辆质心处的位置、速度和加速度估计值，同时也包含了车辆的姿态和角速度值。


图7 X1电动汽车

表Ⅲ 车辆模型参数


控制器在Ubuntu 16.04的传统机载计算机上运行，i7-6700 CPU 以 4.0 GHz 运行。转向角、每个轴上的制动力（映射到制动压力）和驱动力（映射到扭矩）指令被传递到实时计算机以进行下层控制。选择成本函数权重，如表 I所示，将每项指标的合理值统一缩放。例如，50cm的横向位置误差、10 deg/s 的转向速率以及位于障碍物最小安全距离10cm内的位置都对总成本的贡献值为 1。

C.实验

在本次实验中，测试车辆在直线道路上行驶，保持在车道中间。在车辆的质心通过s=180后（图8中的时间①），出现了两个障碍物：一个当前车道的s=200处，另一个在 对向车道的s=215处。此时，车辆开始紧急变道。时间①-⑤在图9、10、11和12中用灰色虚线表示。图13显示了车辆在时间①-⑤处的俯视图。


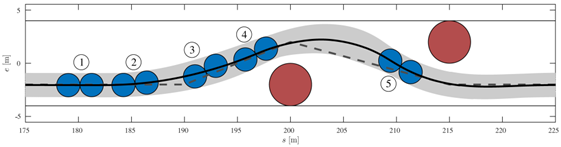
图8 避障工况示意图

控制器计算的闭环输入如图9所示。当障碍物出现在时间①时，控制器开始向左转向，在受转弯速度的限制下最终达到车辆的最大转向角18°。同时，控制器立即将Fxr降低到-4kN，这是一个适度的制动力。这样做的效果是双重的。首先，制动会减慢车辆的速度，使车辆有更多的时间进行横向加速以避开障碍物，从而使操纵更容易。此外，制动时车辆质量转移到车辆前部，从而增加了前轴的横向力容量。控制器利用增加的横向力控制车辆；图10（顶部）显示了在时间①和时间 ②之间增加的横向力及其极限。

相反，图10中所示的后轴横向力在时间①之后容量降低，这既是由于制动时重量从后轴转移到前轴，又由于施加的纵向力(4)所导致的最大横向力降低。当障碍物出现在时间①时，前轴上所有可用的力都需要用于转弯，但后轴可以自由制动，直到车辆转弯至需要后轴横向力为止。控制器能够使用前轴上所有可用的摩擦力来转动车辆，同时仍然在几百毫秒内制动后轴，其他情况则不需要制动。在时间 ②，控制器开始制动前轴（图9中间位置）并放松后轴制动器，将Fxr增加到零（图9下部）。前轴轮胎力在时间②时饱和，前轴制动力的增加意味着前轴横向力的减少，如图 10（顶部）所示。


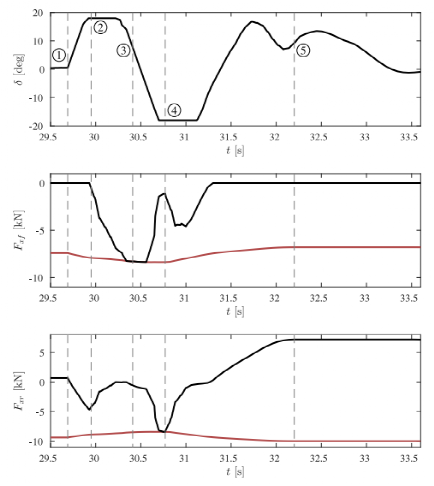
图9 输入变量变化曲线


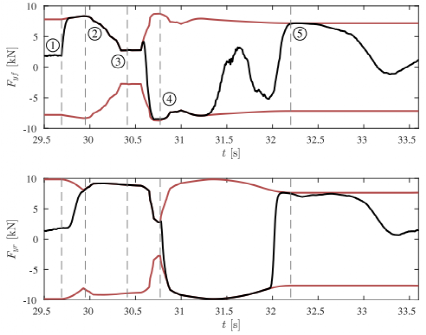
图10 横向力（黑色）及其峰值曲线（红色）

到时间③时，Fxf已接近其最小值，只为Fyf留下少许力容量。此时，车辆已经足以避开第一个障碍物，这将允许控制器给前轴提供一定的制动时间。由于后轴需要大量横向力来稳定和转弯车辆，故大约在时间③时，控制器无法制动后轴。到了时间④时，情况发生了逆转：车辆需要向右变道并产生较大的反向力以避免偏离道路，因此将前制动力降低到几乎为零。同时，有一段短暂的时间，用于稳定的后轮胎横向力从正转变为负；控制器利用这段短暂的时间来制动后轴。

在时间④时，车辆接近第一个障碍物。每个车辆圆和每个障碍物圆之间以及每个车辆圆和道路边缘之间的最小距离如图 11 所示。控制器需要控制车辆进行足够转向以避免偏离道路或撞到第二个障碍物，但不要太度因为此时车辆过于靠近第一个障碍物。就在时间⑤之前进行了类似的权衡，其中控制器减小了转向角（图9顶部），导致负Fyf使车辆远离第二个障碍物，但不会太大以至于车辆无法留在道路上。

很明显，控制器在横向力和纵向力之间进行了很大的权衡，在可能和必要时减慢车辆以完成双车道变换。车辆的纵向速度变化如图12所示。控制器能够在2秒多一点的时间内将车辆从约17.5m/s减速到约8.5m/s。尽管速度大幅降低，但当车辆通过第二个障碍物时，前后轴在时间⑤附近都达到饱和。如果车辆按照初始速度17.5m/s运动，将不可避免地撞上某一个障碍物或者冲出道路。此外，由于控制器非常依赖于在前轴和后轴之间的制动力分配，因此人类驾驶员很难或可能不可能使用单个制动踏板在不发生碰撞的情况下完成此操作。


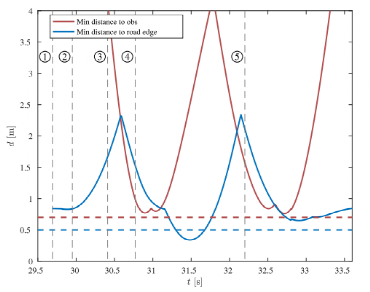
图11 车辆圆与障碍物圆和道路边缘之间的最小距离


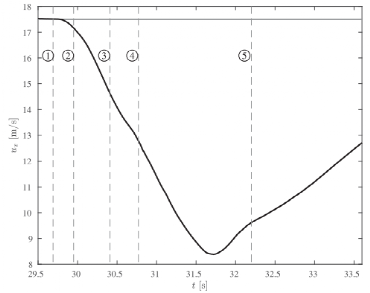
图12 纵向速度变化


图13 车辆运动的俯视图

6 结论

在本文中，我们提出了一种非线性模型预测控制器，能够产生转向角和前后纵向力，以安全地引导车辆越过潜在危险。选择车辆模型、积分器以及车辆和障碍物的表示方法以实现快速计算，从而使车辆能够对环境变化作出快速反应。车辆和障碍物的详细表示可以表示车辆受潜在碰撞的影响，并使控制器能够推理出转弯时车辆的纵向和横向位置。车辆和轮胎模型捕捉车辆的动力学，并将横向力和纵向力之间的耦合关系通知控制器。测试车辆执行紧急双车道变换的实验结果证明了控制器能够平衡前后轴的横纵向力以实现避障功能。


参考文献