基于实测上路数据的电池寿命衰减的理论研究

1  背景

通过数据对汽车零部件状态作分析和故障诊断，是当前汽车工业数字化转型的重点应用方向。其中，汽车动力电池是汽车的核心部件，是研究和应用的重点。数据分析的数据来源于试验环境和实际路况。实际路况下的数据比试验环境下复杂得多，目前仍然没有实际应用。针对汽车在购买后的实际使用数据，建立动力电池的评估模型来评价和预测电池寿命显得十分重要。

当前，基于数据的电池寿命衰减分析仍然主要基于试验室数据的一些理论研究。基于实际上路后数据的电池状态分析和应用尚属空白。

另外，试验室通过循环放电等手段估算循环寿命，而在实际使用中，循环放电信息基本不可得。建立以实际使用时间为输入参数的模型，有十分重要的现实应用意义。

本文对基于实际上路的汽车数据的电池寿命衰减分析给出理论假设模型，并结合实际数据给予验证。

2  假设

本文提出如下模型假设:

假设1: 电池衰减因素主要由内在因素决定，为单调下降函数模型。

假设2: 电池状态受到外界因素的影响，影响因素是用户行为，干扰因素是环境温度。例如，用户行为如充电习惯影响到电池的衰减速率;温度随季节变化时，电池容量也会随之变化。

假设3: 电池状态可以由内因影响和外因影响叠加确定。

示意图如图1所示。



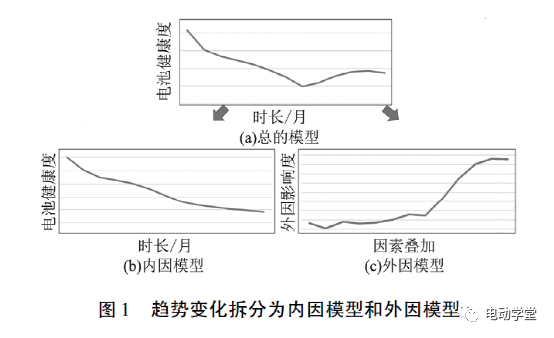
3  试验方法

3．1  试验设计思路

通过拟合基本模型和偏移模型形成数据模型并验证模型精度，据此设计了如下试验:

(1) 对电池状态(SOH)趋势数据做分解，分解为基本模型和偏移模型，分别对应内在因素影响模型和外在环境因素影响模型。

(2) 对分解数据建立模型，通过拟合幂函数、指数函数等函数建立主要趋势线的统一函数模型，通过拟合波动线建立符合波动变化的模型。

(3) 用拟合的模型对实测数据做拟合分析。拟合的模型可用于实际数据预测电池状态变化。

3．2  试验设计方案

3．2．1  试验数据

对于实际使用数据，提取2万辆混合动力汽车的充电记录，通过深度充放电记录计算每辆汽车(以VIN为ID标识)每个月的SOH。

3．2．2  试验方法

(1) 拟合内因模型

基于统计、经验和参考数据，选择最佳函数拟合线。

① 统计数据，对已有样本统计平均SOH等。

② 统计规则应用，根据统计规则进行模型偏移调整，比如单调下降函数。从统计数据来看，电池的衰减表现为开始3个月急剧下降，后面下降趋缓。因此，应构造分段函数表达整体模型。

③ 参考数据应用，比如试验室SOH衰减数据。

④ 最佳函数拟合:测试多种函数形态，得到最佳函数(最佳分段函数)形态，以及相应的最佳参数，比如线性、二次函数、幂函数、指数函数，此处采用牛顿迭代法。

(2) 拟合外因模型

① 计算波动，做周期识别:固定间隔(3个月、6个月、1年等)，判断周期。

② 通过实际使用数据识别因素对衰减速率影响规律，调整波动及波幅。

③ 对波动振幅做衰减。

(3) 整合两个模型，建立统一模型。

(4) 对函数拟合进行验证，利用函数进行预测。

3．3  试验结果

3．3．1  内因线模型拟合试验

设计和测试了几种衰减函数，采用拟合优度对函数模型进行评估。

首先用单个模型为代表，拟合数据如表1所示。



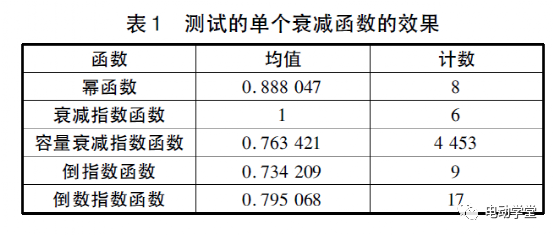
从表1可以看出，容量衰减指数函数是拟合最多的模型，而衰减指数函数拟合程度最好。

因为电池寿命衰减的表现是开始下降剧烈，后面下降趋缓，故用不同的衰减函数模拟前半段和后半段。

从分段函数效果来看，仍然是衰减指数函数拟合的数量最多，幂函数拟合的数量也比较多，见表2。



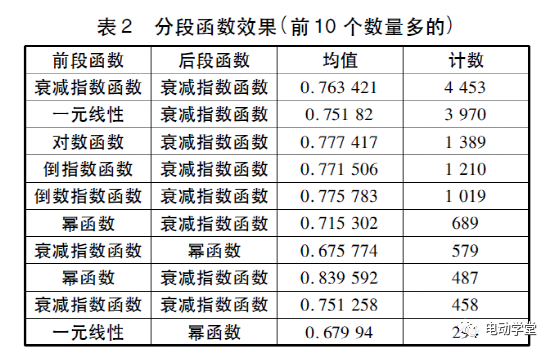
从分段函数效果来看，指数函数和幂函数拟合的效果比较好，见表3。



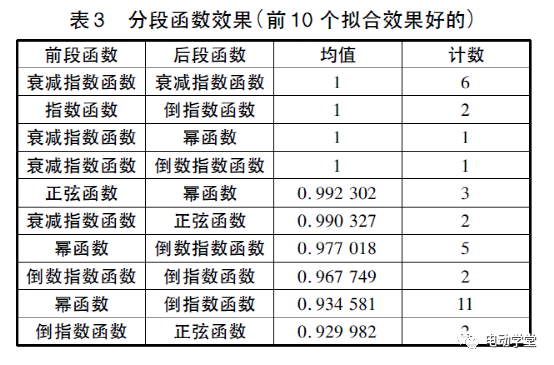
由以上数据分析可见，电池衰减模型以指数函数为主，也可能呈现幂函数形态。这些和现有试验室的数据研究初步结论相符。

3.3.2  外因线模型拟合试验

根据经验可知，电池寿命的影响因素有油电比例、温度、均衡时长比例、放电功率、回馈功率和高低SOC的存储比例。

筛选车辆历史数据，选取衰减速率在前20%和后20%的数据，计算和分析其各影响因素对电池衰减速率的影响度，结果如表4所示。



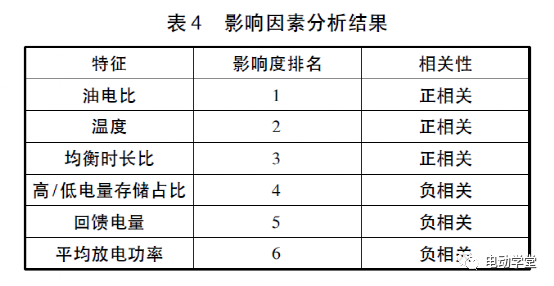
基于上述结论，进行外因模型的设计，可假定每个影响因素都可以通过一个算式模型表示，那外因模型为多个算式模型组合变化而成，并存在以下约束:

(1)特征约束

·  影响因素均可人为识别;

·  特征发散，无方差接近于0的样本。

(2)数据约束

·  在每个时间点，数据符合正态分布，用平均值估计，误差也为正态分布;

·  极端样本占比小，一定置信度下预测误差有界。

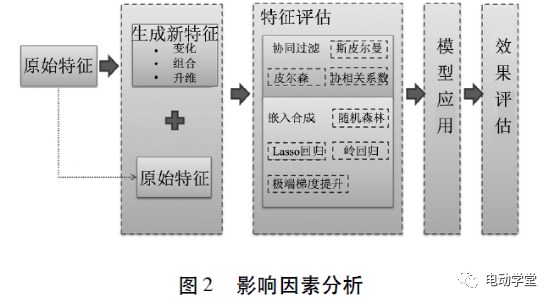
通过多种算法的整合，以获得更准确的识别，整合方法如图2所示，获得影响因素的模型，并得出以下结论:

(1) 单维度变化的影响:固定其他维度的值;梯度方向变化维度值;查看Y的变化。

(2) 多维度联动

由多次单维度变化构成。

(3) 如局部最优解存在，就一定可以收敛到局部最优解。

因此，外因线可以用多项式模型和傅里叶变化模型进行搭建，并且可获得局部最优解。



4  模型应用

如上模型应用于上汽荣威APP“电池医生”，能够全方位评估车主的用车状况，并给出电池使用建议，取得了良好效果。

方法如下:

(1) 拟合出模型，确定参数;

(2) 利用拟合的模型，预测SOH。

利用预测的精度表达预测的准确度，实际结果如表5所示。



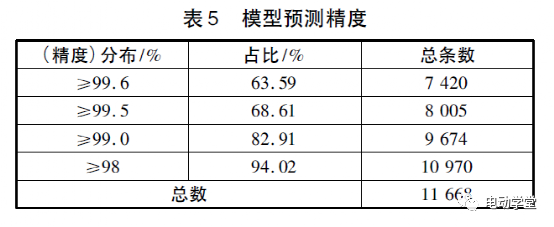
由表5可见，预测达到了较高的精度，说明假设模型具有很强的实用性。

5  结语

汽车动力电池的主要趋势符合指数函数的单调递减序列函数模型。在实际应用中，温度是除了主要内因以外的最主要的影响因素。内因和外因影响叠加，可以构成汽车动力电池的衰减模型。应用此原理，可以通过拆分对电池寿命进行预测。试验数据符合该假设，在实践中取得良好效果。

动力电池状态和衰减分析预测以动力电池寿命预测和保养策略的多模型融合的技术创新为突破口，填补了国内在PHM平台技术领域的空白，已申请4项专利。上汽正在积极推动新模式的业务架构，探索算法在传统制造业的创新与落地，以场景和用户为导向，为促进大数据和人工智能技术在汽车行业应用中的落地打下良好的基石。