中高频轮胎动态特性建模
1、在平面内和平面外小于8Hz,路径波长大于10倍印迹长度,轮胎表现为整体弹性,侧向和纵向可以用非稳态特性描述;
2、在平面内小于80Hz,平面外小于60Hz,短波长路面,即路径波长接近一倍印迹长度,轮胎振动以刚体模态为主;
3、在平面内大于80Hz,平面外大于60Hz,轮胎振动出现带束弯曲模态。

1、建模背景
轮胎在各种激励下的振动特点,下图是轮胎模态试验的试验结果,不同的振动频率下,它的振型、固有频率、阻尼比(T表示平面外的振型,R表示平面内的振型)。可以发现在一定频率范围内,胎体和带束会保持一个整体的振动模态,在更高的频率激励下,轮胎会出现弯曲模态,更高阶次的振型。轮胎的模态与轮胎的约束状态是有关系的,这个模态试验是在自由状态下,轮胎接地之后,各阶振型的固有频率会发生变化。H.P. Willumeit和F. Böhm学者认为,平面内的振动模态只出现在最高8阶(大概250Hz),更高的频率振动属于胎侧的波动,而且具有强阻尼特性。
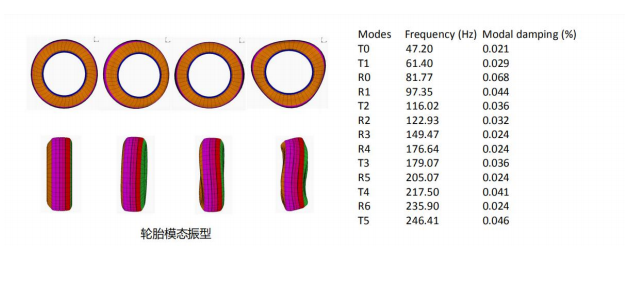
2、刚性环模型
这是刚性环模型的一个结构简图(包括轮辋),左图是表示带束的刚性环,轮辋与刚性环之间有简化的、三个方向的、轮环之间的弹簧和阻尼,带束环与地面有接地弹簧、切向方向是松弛、滑移模型。这个刚性环模型采用的是单点接触模型,轮辋与带束环之间的弹簧通过模态分析,大概估算出它的数量级在 10^6,而轮胎的整体弹性,从轮心到地面的刚度在10^5,所以引入了接地弹簧来表示轮胎的整体弹性。在水平的切向,采用的是UniTire建模方法,SWIFT里面采用的是MF建模方法。不管是刚性环模型还是离散胎体模型都表现带束与轮辋之间的一种相对运动,我们需要把轮胎的整体质量做一个分配假设,胎圈这部分属于轮辋的质量,胎面属于带束,胎侧一部分分配到轮辋上,一部分分配到带束环上。
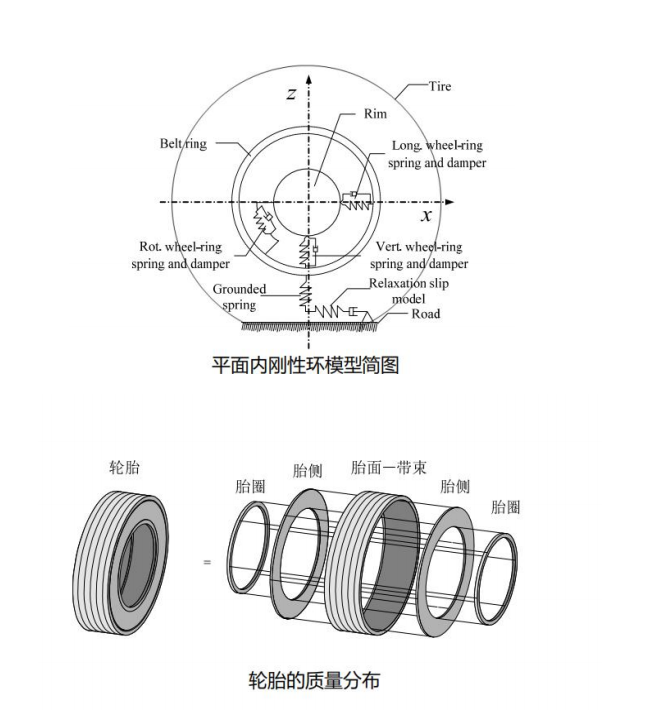
从这个刚性环动力学方程可以发现,这两个方向的耦合量其实就是Z 向,相对是比较小的。在用刚性环模型的时候会把这项忽略掉,在一定的范围内,误差也不是太大。

3、轮胎高频离散模型
3.1 胎体、胎面离散模型
轮胎在比较高频的激励下,带束有弯曲的模态,所以我们把带束离散成一系列质量点,质量点只有移动自由度,这些质量点与轮辋之间有相应的径向、切向弹性和阻尼相连,质量点之间也有弹簧单元相连。为了模拟带束的抗弯特性,在三个质量点之间加入了弯曲弹簧,因为质量点的相对变形比较小,所以我们引入一个相对坐标系,相对坐标系里来表示质量点的相对变形,在绝对坐标系里表示质量点的动力学方程。为了计算胎面的接触,还要引入一个地面的局部坐标系。
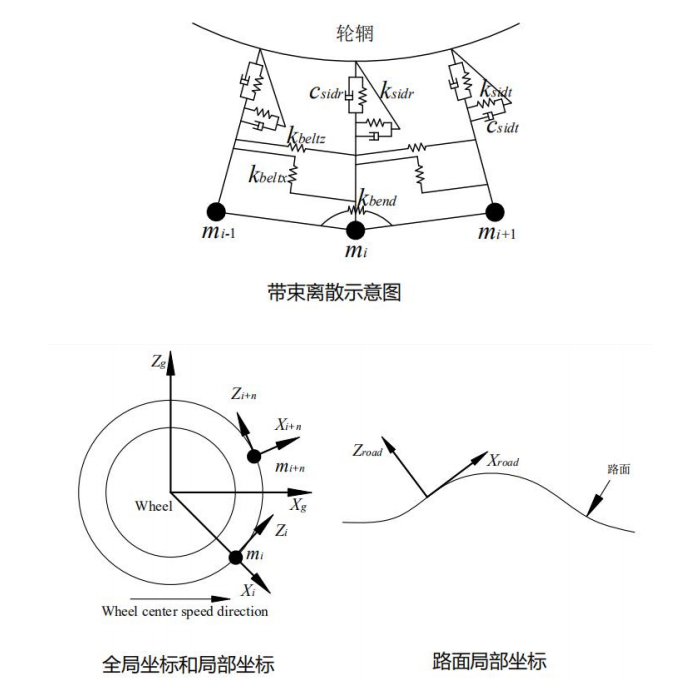
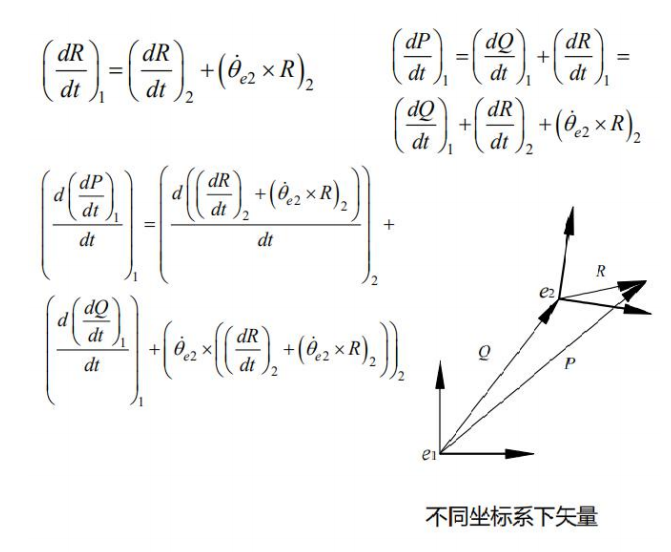
下图是质量点绝对位移矢量加速度的表达式,这里面包含了质量点相对位移矢量、局部坐标的转动、局部坐标原点的位移,我们用这个动力学关系求解每个质量点的动力学方程。
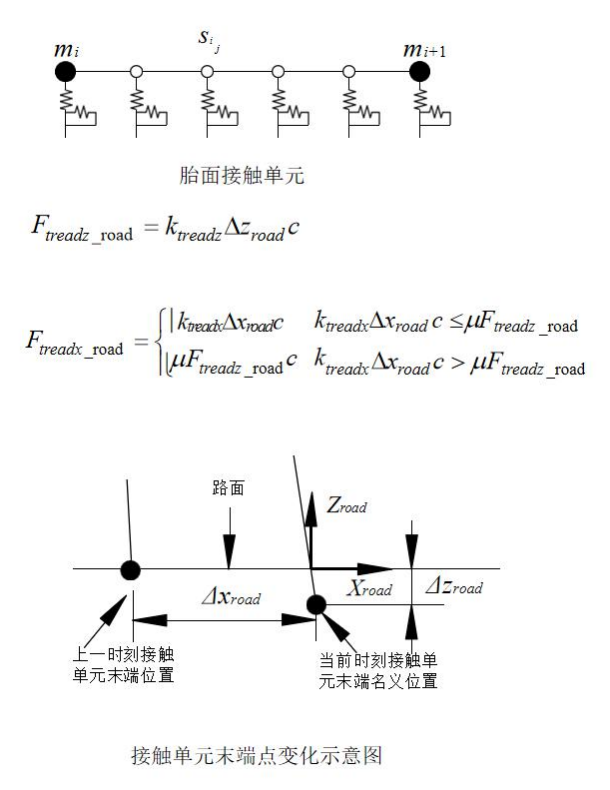
在平面内模型中,因为一个质量点就有两个自由度,质量点越多,自由度就越多,动力学方程越多,计算量就越大,所以我们要合理的选择质量点的个数,但是我们又希望接触的时候计算结果更准确,我们在质量点之间插入了无质量的胎面接触单元,来计算胎面与路面的接触特性。这是接触单元接触时候末端点变化的示意图,在计算的时候要用接触和附着来判定每个计算点的当前位置。
这是系统轮辋的动力学方程,轮辋也是有三个自由度,两个平动一个转动。
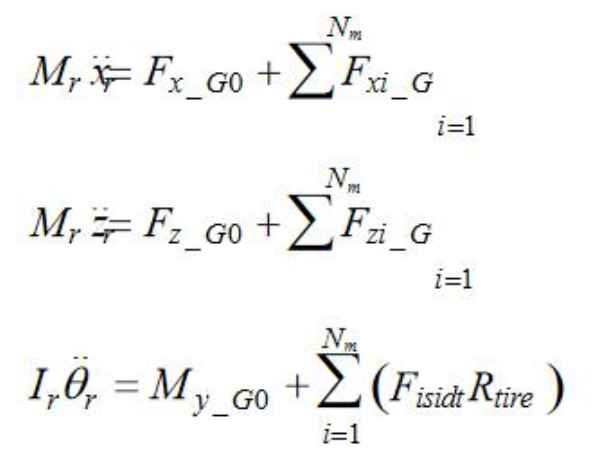
下图是每个质量点的动力学方程。
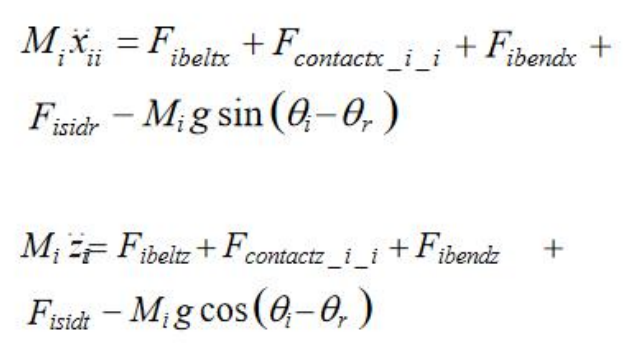
3.2 胎面单元的摩擦模型
因为胎面单元的摩擦特性,它不是遵守传统的库伦摩擦,比较复杂,受很多因素:比如说温度、滑移速度、压强等多个因素影响。我们目前采用的是一个经典的savkoor公式来描述橡胶的动摩擦系数。
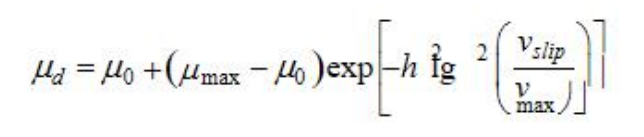
3.3 数值算法
我们目前是采用Newmark和牛顿迭代相结合的方法。Newmark方法是一种直接积分法,基本思想是将时间离散化并使时间间隔足够小,将微分方程组近似为代数方程组,由已知的t时刻响应求解t+Δt时刻的响应,从而求出所有时刻的响应。
Newmark方法将求解轮胎动态模型动力学方程问题转换为求解代数方程问题:即求解方程。牛顿迭代法具有收敛速度快的优点,但是该方法是受初值选择的影响较大。
3.4 模型验证
所建轮胎动态模型在时域和频域都有较好的表达精度。低频区动态模型和试验数据的频率特性一致,在高频区域,两者的频率特性有一定差异,但趋势一致。由于该区域的振动能量很小, 所以这种差异对轮心的力学输出影响也可忽略。所建立模型频率适用范围可以达到200Hz。在该模型结构下,采用C语言进行运算,解算速度可以达到约0.95倍的实时时间。
最新资讯
-
沃尔沃汽车:创新驱动的豪华品牌
2025-04-24 18:16
-
飞书项目落地ASPICE解决方案,助力汽车软件
2025-04-24 09:59
-
驾驶员监控系统DMS合规认证的“中西结合”
2025-04-24 08:23
-
自动驾驶汽车测试关键行人场景生成
2025-04-23 17:12
-
R171.01对DCAS的要求⑧
2025-04-23 17:08





 广告
广告





























































