基于线性变参数系统的四轮转向自主地面车辆路径跟踪控制及实验验证
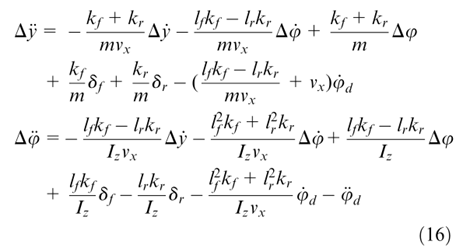

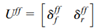



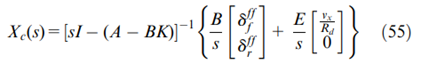 ,
,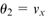 和
和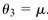 。变参数向量定义为
。变参数向量定义为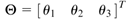

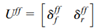
 的仿射模型可以写成
的仿射模型可以写成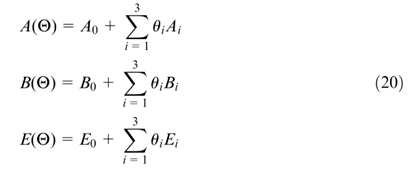

 (i=1,2,3),因此,变参数向量
(i=1,2,3),因此,变参数向量 有八种组合形式
有八种组合形式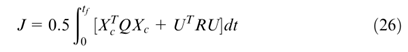
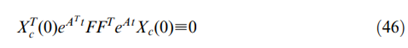 (j=1,2,…8),等式(20)可以改写为
(j=1,2,…8),等式(20)可以改写为
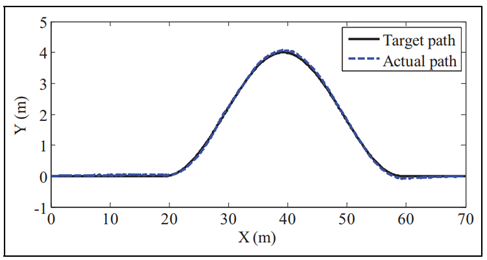
 是八个顶点的权重。此外
是八个顶点的权重。此外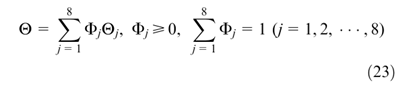
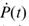
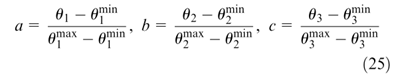
编辑推荐
最新资讯
-
中汽中心工程院能量流测试设备上线全新专家
2025-04-03 08:46
-
上新|AutoHawk Extreme 横空出世-新一代实
2025-04-03 08:42
-
「智能座椅」东风日产N7为何敢称“百万级大
2025-04-03 08:31
-
基于加速度计补偿的俯仰角和路面坡度角估计
2025-04-03 08:30
-
《北京市自动驾驶汽车条例》正式实施 L3级
2025-04-02 20:23





 广告
广告





























































