拉格朗日乘子向量

定义为
由于
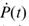
在稳态下可以视为零,所以P(t)是以下黎卡提方程的解
在计算出P(t)之后,将等式(31)代入等式(29)得出
在LQR控制器设计中,Q和R分别给定为Q=diag[1000,10,300,3],R=diag[1,2]。
至于LQR反馈控制器方程(34),它不能处理外部干扰。这个问题将在第4.3节中解决。首先,用LQR控制器对闭环系统进行稳定性分析。如果外部干扰暂时被忽略,那么
为了分析闭环系统方程(36)的稳定性,我们首先引入以下引理。
引理1:如果线性时不变系统方程(35)中存在扰动D(t),即
,其中D(t)独立于控制向量U,则扰动D(t)不会改变系统方程(35)的可控性。
由于本文中的扰动是由独立于控制向量U的
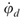
和
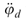
组成的,因此可以得出结论,扰动不会改变系统方程(35)的可控性。
引理2: 对于线性时不变系统方程(35),它具有用于状态反馈LQR控制器设计的性能指标方程(26)。如果{A,B}是可控的,且{A,F}是可观测的,其中FF=Q,则闭环系统方程(36)是渐近稳定的。XcPXc是一个李雅普诺夫函数,其中P是一个对称正定矩阵,它是黎卡提方程(33)的唯一解。
其中,当且仅当
。由于
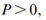
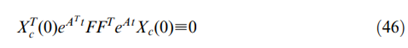
。因此,等式(37)是一个李雅普诺夫函数。很显然满足下式:
由于Q是一个半正定矩阵,而R是一个正定矩阵,
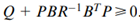
。因此
如果
。根据方程(40),可以得到:
由于
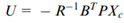
,等式(44)可以写为:
由于

,可以推导出
。因此,该系统方程的零输入响应可以表示为:
它和
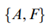
是可观察的条件是相矛盾的。因此,假设
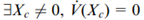
是错误的。
最后,可以得出结论,闭环系统方程(36)可以看作是全局渐近稳定的。这证明了引理2。
从方程(34)可以看出,控制向量U仅与状态向量Xc相关。它不能处理外部干扰

。

是可以得到的,并由

和
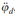
组成。因此,采用前馈控制来减小外部干扰引起的路径跟踪误差。
根据上述分析,路径跟踪控制器可以表示为前馈控制器和LQR反馈控制器的和。
需要求解,并根据方程(34),LQR反馈控制器可以表示为:
假设状态向量的初始值为零,经拉普拉斯变换后,式(50)可得改变成:
其中
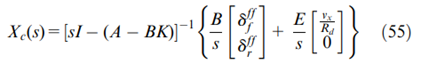
表示对变量向量进行拉普拉斯变换。
如上所述,假设
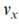
是常数。可以得到:
根据拉普拉斯变换的终值定理,系统状态的稳态误差可以表示为:
如果
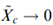
,可以得到:
为了简化轨迹跟踪控制器的设计过程,在控制器设计和稳定性分析中使用了模型方程(17)。事实上LPV模型用于最终控制器设计。考虑到以下由方程(22)描述的LPV闭环控制系统具有八个顶点,LPV-LQR控制器应该表示为八个惯性控制器的加权和。等式如下:
其中,
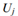
是第j个顶点模型的第j个控制器,可根据等式(49)和(59)计算得出。
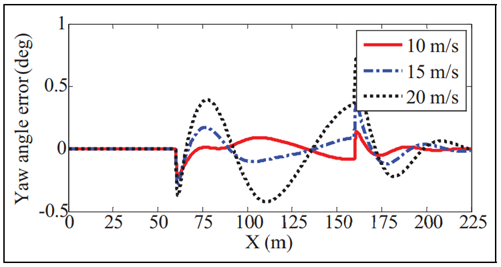
为了评估所设计控制器的路径跟踪性能,通过CarSim-Simul
ink平台使用高度准确的整车模型进行联合仿真。4WS AGV路径跟踪仿真框图如图5所示。仿真中4WS AGV的结构参数如表1所示。在车辆测试,双车道变换(DLC)是最常见和最典型的动作之一。它可以很好地评估车辆的横向动力性能。对于自动驾驶
汽车,DLC 机动也是一个至关重要的动作。该测试不仅可以验证控制器的路径跟踪性能,还可以评估车辆的操纵稳定性。因此,选择DLC作为条件。
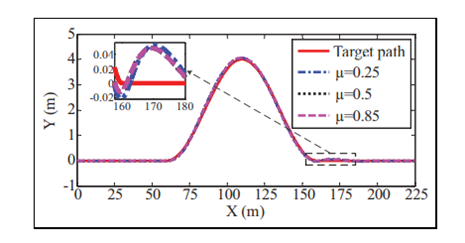
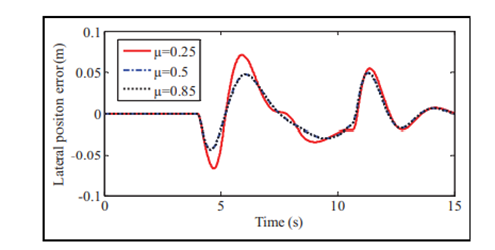
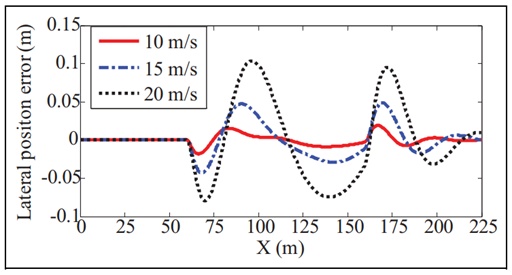
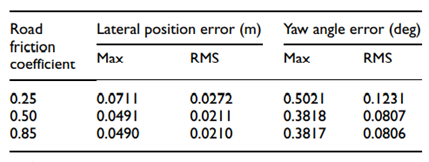
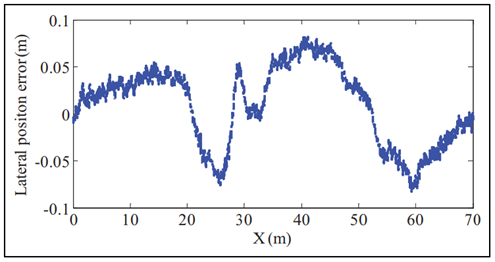
在本仿真案例中,4WS AGV以不同的路面摩擦系数进行DLC机动,旨在验证所设计控制器的路径跟踪能力。此外,它还可以评估该路径跟踪控制器对不同路况的鲁棒性。4WS AGV的纵向速度设定为15m/s,道路摩擦系数设定为0.25,0.5和0.85来模拟不同路面条件,即结冰路面、湿路面和干路面。
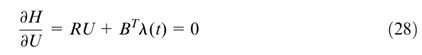
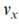
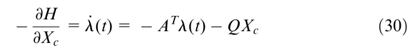
 定义为
定义为

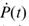 在稳态下可以视为零,所以P(t)是以下黎卡提方程的解
在稳态下可以视为零,所以P(t)是以下黎卡提方程的解


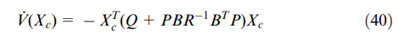
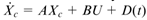
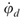 和
和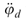 组成的,因此可以得出结论,扰动不会改变系统方程(35)的可控性。
组成的,因此可以得出结论,扰动不会改变系统方程(35)的可控性。
 。由于
。由于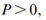
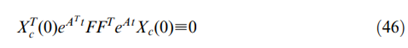 。因此,等式(37)是一个李雅普诺夫函数。很显然满足下式:
。因此,等式(37)是一个李雅普诺夫函数。很显然满足下式: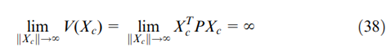

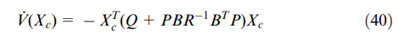
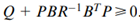 。因此
。因此
 。根据方程(40),可以得到:
。根据方程(40),可以得到:
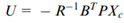 ,等式(44)可以写为:
,等式(44)可以写为:
 ,可以推导出
,可以推导出 。因此,该系统方程的零输入响应可以表示为:
。因此,该系统方程的零输入响应可以表示为: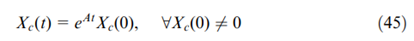
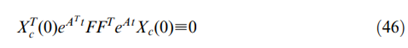

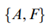 是可观察的条件是相矛盾的。因此,假设
是可观察的条件是相矛盾的。因此,假设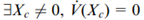 是错误的。
是错误的。 。
。 是可以得到的,并由
是可以得到的,并由 和
和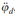 组成。因此,采用前馈控制来减小外部干扰引起的路径跟踪误差。
组成。因此,采用前馈控制来减小外部干扰引起的路径跟踪误差。
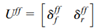
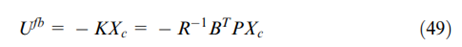


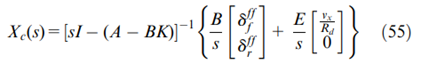 表示对变量向量进行拉普拉斯变换。
表示对变量向量进行拉普拉斯变换。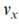 是常数。可以得到:
是常数。可以得到:


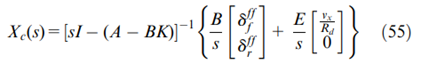
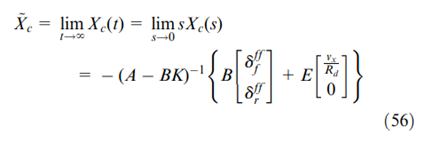
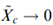 ,可以得到:
,可以得到:
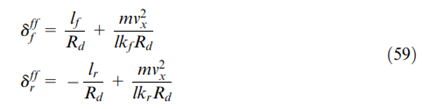

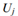 是第j个顶点模型的第j个控制器,可根据等式(49)和(59)计算得出。
是第j个顶点模型的第j个控制器,可根据等式(49)和(59)计算得出。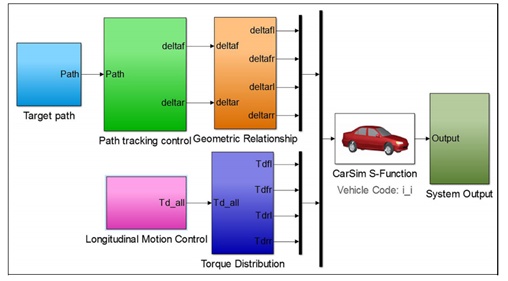







 广告
广告





























































