广告
NVH测试中的扭振测试
2021-09-12 21:00:21· 来源：汽车NVH云讲堂
1、为什么会产生扭振？旋转部件自身产生扭振轴的静态扭转-对于单独的一个轴而言，在轴两端施加一对外力偶，由于轴并不是绝对的刚性体，各个轴段的微小截面均会产
1、为什么会产生扭振？
旋转部件自身产生扭振
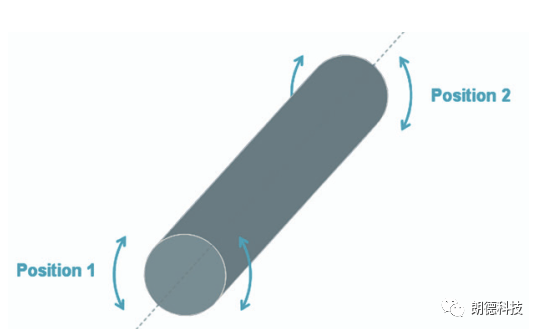
轴的静态扭转-对于单独的一个轴而言，在轴两端施加一对外力偶，由于轴并不是绝对的刚性体，各个轴段的微小截面均会产生位移，进而轴端的两端面会产生一个相对的旋转角。这种现象称为轴的静态扭转。
轴的动态扭转-然而当轴在运动系统中旋转时，由于轴端受到的力和力矩是变化的，因此除轴沿轴线的刚性旋转运动外，轴的各端面也会存在相对的扭转振动，进而表现为轴旋转时转速的波动。
2、传动系统产生扭振
整车动力NVH问题除来自发动机本体的振动、噪声及其传递外，还有相当一部分可能会来自于发动机、变速箱、传动部件和行驶系统在旋转激励下引起的系统扭转振动，简称扭振。
传动系统扭振主要来源于发动机燃烧压力波动和曲柄连杆系统部件的惯性载荷变化，当系统中离合器、弹性联轴器等扭转减振机构匹配不当，就可能会产生扭振问题，从而在整车上表现出如耸动、低频抖动、变速器敲击、车内轰鸣、车内地板振动等NVH问题。因此，对传动系统的扭振问题进行管控对于NVH性能的开发具有十分重要的意义，在开发前期可以通过CAE方法对传动系统扭振进行仿真与优化，而在样车调校阶段则需要基于对扭振的测试来进行分析和改进。通过对传动系统各个节点的扭振进行测试，一方面可以用于对传动NVH子系统的开发目标的进行评估和验收，另一方面，也是解决传动系统相关的NVH问题的重要手段。
整车传动系统扭振测试
3、扭振信号的采集
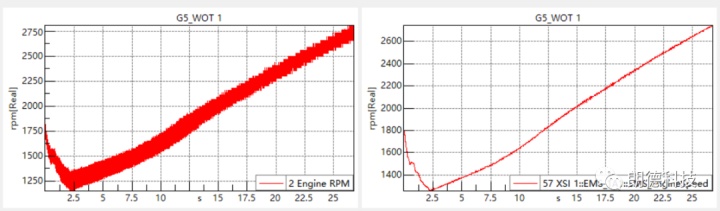
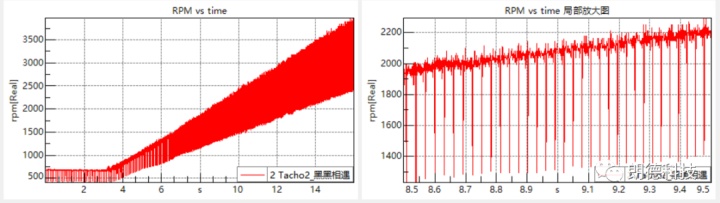
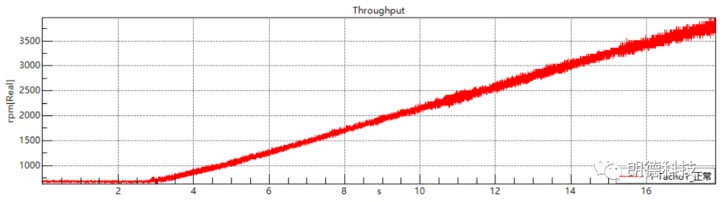
通常在对扭振信号进行测试时，我们最常用的测量物理量是转速即RPM vs time曲线。通过转速波动来反应扭转时振动的大小。采集的转速信号如下图：
左图：扭振信号 右图：CAN信号中的转速信号
我们发现，采集到的转速信号要比CAN信号或者直接测得的转速信号要“粗”很多，这正是由于轴转速的波动引起的。为了测得旋转轴的转速波动，我们需要对轴的旋转运动进行再进一步的“精细化”划分，以码带测试的方法为例，我们将旋转一周的运动划分为60份或者更高，通过测得每条色带的速度得到一个更加精细的转速变化，进而研究转速的波动情况。
那么我们如何精细地采集转速的波动呢？一般我们会用到三种方式，分别是：利用电磁效应的转速传感器+旋转齿轮、光电转速传感器+码盘/带、编码器三种方式，接下来就详细为大家介绍一下三种采集方式的原理及特点。
（1）利用电磁效应的转速传感器+旋转齿轮
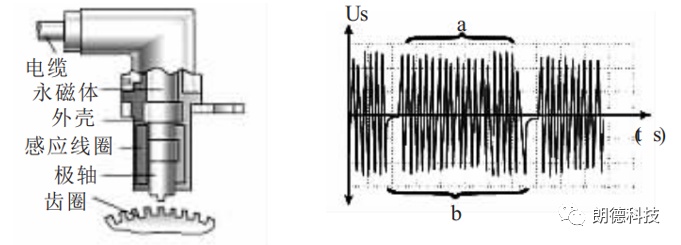
此类传感器根据原理可分为两种，一种是利用电磁感应原理工作的，当齿圈的齿顶与传感器的极轴端部相对应时，通过磁感线圈的磁通量最大。当齿圈的齿隙与极轴端部对应时，通过磁感线圈的磁通量最小。感应线圈中磁通量的变化产生交变电动势。
左：磁电式转速传感器结构 右：磁电式转速传感器波形图
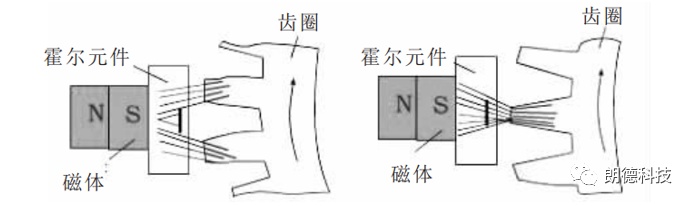
另外一种是利用霍尔效应原理工作的，当齿圈转到齿隙与霍尔元件对正时, 永磁体传到霍尔元件的磁力线分散, 磁场较弱, 输出的霍尔电压较小。当齿圈转到一个齿与霍尔元件对正时, 永磁体传到霍尔元件的磁力线集中, 磁场较强, 输出的霍尔电压较大。
霍尔传感器工作原理
（2）光电传感器+码盘/带
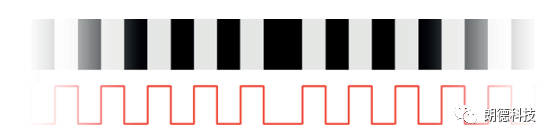
传感器端部发出光线(一般为红色可视光)，将码盘粘贴至旋转物体的端面，当光线照射到码盘上产生反射光，并检测出码带的反射光进而得到转速的脉冲信号。
（3）编码器
编码器是一种分辨率极高的精密传感器，其旋转一圈有的甚至可达到几千个脉冲，如果一个编码器旋转一圈会产生1000个脉冲，当转速达到5000rpm时，一秒就可以产生83000个脉冲信号，因此扭振测试对数采采样率要求较高，MECALC数采的转速采集通道可达到1M pulse/s的采样率，可以应对各种普通转速信号的采集以及扭振测试。
4、扭振信号的处理
在扭振测试试验中，我们测得的信号是脉冲信号，通过设置触发电平可以得到转速随时间变化的曲线，也就是角速度随时间变化的曲线。而我们扭振试验的研究对象是角度，因此我们在测得原始信号后，需要对该信号进行一次积分才能得到我们想要的结果。
另外在实际试验过程中，如果使用码带对旋转轴进行测试，在码带的连接处，必然会存在不连续的情况。在使用齿轮盘进行测试时，如果存在缺齿的现象，也会引起转速的不连续现象。这两种情况都会引起转速信号的急剧波动，给信号处理带来了困难，那么这种情况应该如何处理呢？
原始信号中由于码带不连续或者缺齿引起的信号“缺失”
由于缺齿或者码带的不连续导致的转速错误
（1）码盘/带粘贴的特殊情况处理
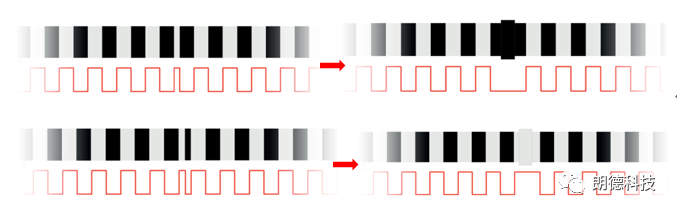
在实际的信号采集的过程中，在粘贴码带的过程中，由于粘贴位置和色带宽度的不匹配，常常会遇到“色带重叠”以及相交处色带只有部分窄带的情况。
色带重叠
当出现色带重叠，传感器扫过重叠位置时会使方波信号有较长的一段时间处于低电平或高电平，从而引起转速的计算错误；当出现窄带时，由于窄带可能过窄，传感器扫过窄带位置时会使方波信号也出现一个窄带的高电平或者低电平，亦会引起转速的计算错误。对于窄带的的处理，我们一般会选择用相同颜色的色带将其粘贴至一起，做成一个色带，使其效果变成“色带重叠”的效果，进而保证码带上只有一个结合处并按照色带重叠进行计算。如下图所示：
人为码带处理的两种情况
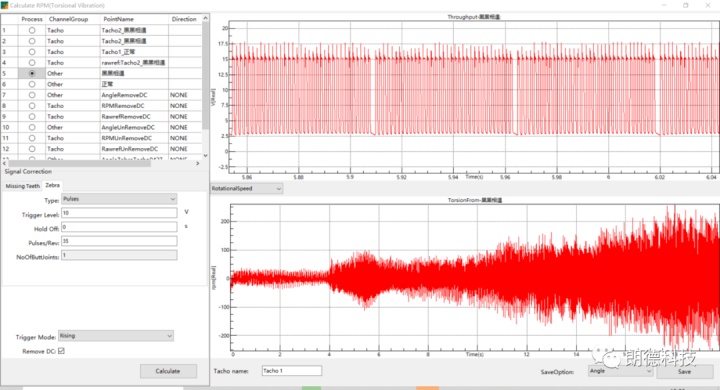
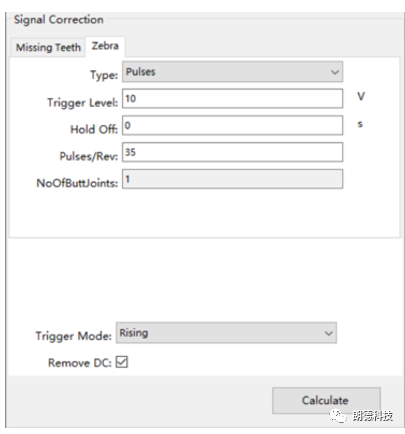
在ATOM软件内算法可以允许用户设置触发电平，每圈脉冲数以及结合处的数量，软件会自动将码带结合处的方波信号进行处理，得到正确的转速波动以及角度波动的信号。
码带信号处理的设置
（2）齿轮缺齿的特殊情况处理
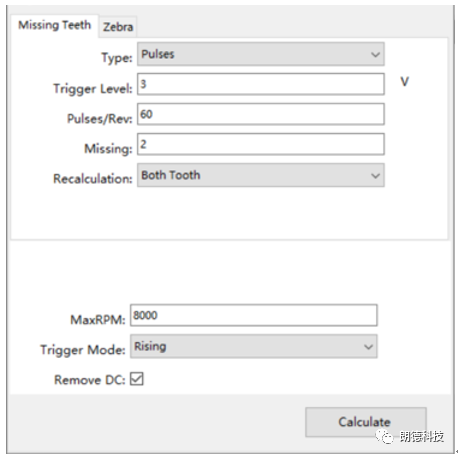
对于齿轮缺齿而言，软件内允许用户设置触发电平，每圈脉冲数以及缺齿的数量。设置好参数后软件可自行进行补齿计算，得到正确的转速波动以及角度波动。
缺齿信号处理的设置
在对于码带结合处以及齿轮缺齿处的信号进行处理之后，我们就会得到一条正常的转速随时间波动的曲线。
经过处理后的转速信号
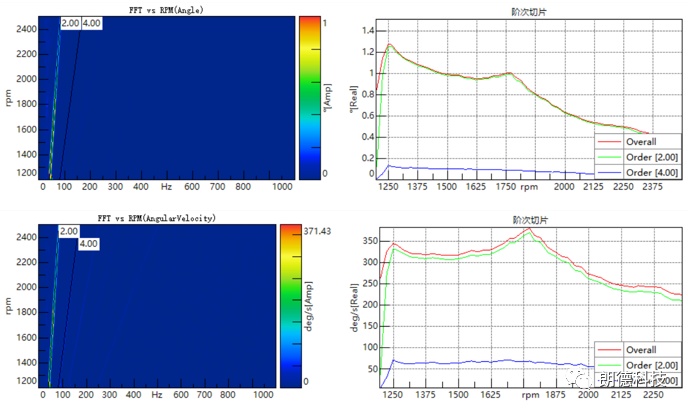
ATOM软件在后期的处理中将转速的曲线进行一次积分转变为角度信号并对其进行FFT运算，得到对应的colormap图以及相应的阶次切片图，如下图所示：
广告
最新资讯
-
奇石乐推出带以太网的新型多功能工业电荷放
2024-09-21 08:49
-
标准立项｜民用机场陆侧区域 智能网联汽车
2024-09-21 08:47
-
精准驾驭电流--ITECH车用电流传感器测试解
2024-09-21 08:44
-
新能力上架 | 电驱系统动态工况加载电磁安
2024-09-21 08:43
-
零束科技携手上海交大加速智能车前瞻技术落
2024-09-21 08:42
广告
广告
