广告
FAST-LIO2: 快速直接的激光雷达-惯性里程计
2021-09-12 21:53:49· 来源：同济智能汽车研究所
收敛后，最优状态和协方差估计为:
随着状态更新
，第k次扫描中的每个激光雷达点(
)通过以下方式转换为全局坐标系：
转换后的激光雷达点{
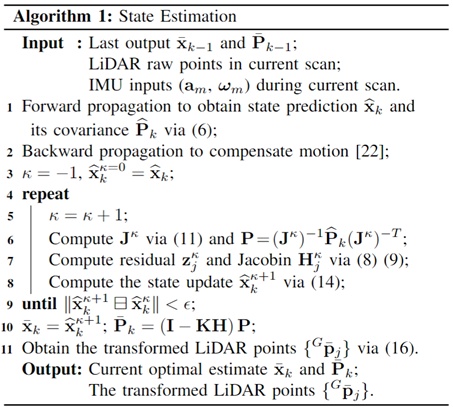
}被插入到由ikd-Tree表示的地图中（参见第V章）。我们的状态估计总结在算法1中，如下。
5 建图
在本节中，我们将描述如何增量维护地图（即插入和删除），并通过ikd-Tree对其执行k-nearest搜索。为了从理论上证明ikd-Tree的时间效率，我们对时间复杂度进行了全面的分析。
A.地图管理
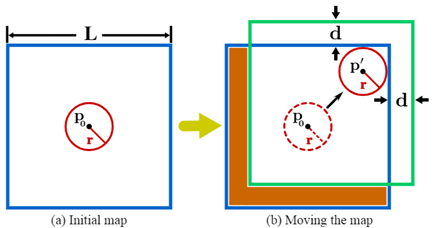
地图点被组织成一个ikd-Tree，它通过以里程计速率合并新的一帧点云而动态增长。为了防止地图的大小不受约束，在ikd树上仅保留激光雷达当前位置周围长度为L的大局部区域中的地图点。2D演示如图3所示。地图区域被初始化为一个边长为L的立方体，它以初始激光雷达位置p0为中心。假设激光雷达的检测区域是一个以从(15)中得到的激光雷达当前位置为球心的检测球。假设探测球的半径为r=γR，其中R是激光雷达视场角范围，γ是大于1的松参数。当激光雷达移动到新位置p'时（在p’处探测球接触到地图的边界），地图区域沿激光雷达检测区域与触摸边界之间距离增加的方向移动。地图区域移动的距离设置为常数d=(γ-1)R。新地图区域和旧地图区域之间的减法区域中的所有点都将通过V-C小节中详述的框式删除操作从ikd-Tree中被删除。
图2 地图区域管理的2D演示。在（a）中，蓝色矩形是长度为L的初始地图区域。红色圆圈是以初始LiDAR位置p0为圆心的初始检测区域。在（b）中，检测区域（红色虚线圆圈）移动到地图边界被触摸的新位置p'（红色实线圆圈）。地图区域移动到新位置（绿色矩形）距离d。减法区域（橙色区域）中的点从地图（即ikd-Tree）中移除。
B.树状结构和构造
1)数据结构：ikd-Tree是一个二叉搜索树。ikd-Tree中树节点的属性在Data Structure中呈现。
k-d树的许多现有实现只在叶节点[43]–[45，53，54]上存储点的“桶”，与此不同，我们的ikd-Tree在叶节点和内部节点上都存储点,以更好地支持动态点插入和树的重平衡。当使用单个k-d树时，这种存储模式在kNN搜索中也表现出更高的效率[41]，我们的ikd-Tree就是这种情况。由于一个点对应于ikd-Tree上的单个节点，我们将交替使用点和节点。点信息（例如，点坐标、强度）存储在point中.属性leftchild和rightchild分别是指向其左右子节点的指针。分割空间的分割轴记录在axis中。以当前节点为根的(子)树的树节点数(包括有效和无效节点)保持在属性treesize中。当点从地图中删除时，ikd-Tree不会立即从树中删除节点，而只是将布尔变量detected置为真（详见第V-C2节）。如果删除以当前节点为根的整个（子）树，则treedeleted设置为true。从（子）树中删除的点数汇总到属性invalidnum中。属性range记录了（子）树上点的范围信息，它被解释为一个包含所有点的外接轴对齐长方体。外接长方体由其每个维度上分别具有最小和最大坐标的两个对角顶点表示。
2）构建：构建ikd-Tree类似于[40]中构建静态k-d树。ikd-Tree沿着最长维度递归地在中间点分割空间，直到子空间中只有一个点。Data Structure中的属性在构造过程中被初始化，包括计算树的大小和(子)树的范围信息。
C.增量更新
ikd-Tree上的增量更新指的在动态重新平衡之后而进行的增量操作，其中动态重新平衡详见第V-D节。ikd-Tree支持两种类型的增量操作：点式操作和框式操作。点式操作在k-d树中插入、删除或重新插入单个点，而框式操作在给定的轴对齐长方体中插入、删除或重新插入所有点。在这两种情况下，点插入都进一步与树上的下采样相结合，从而将地图保持在预定的分辨率。在本文中，我们只解释了FAST-LIO2的地图管理所需的点式插入和框式删除。读者可以参考我们在Github存储库中ikd-Tree的开源完整实现以及其中包含的技术文档以了解更多详细信息。
1)使用树上的下采样进行点插入：考虑到机器人的应用，我们的ikd-Tree支持同时进行点插入和地图下采样。该算法在算法2中有详细说明。
对于来自状态估计模块（见算法1）的中的给定点p和下采样分辨率l，算法将空间均匀地划分为边长为l的立方体，然后是找到包含点p的立方体CD（第2行）。该算法仅保留最接近CD中心点pcenter的点（第3行）。这是通过首先在k-d树上搜索CD中包含的所有点，并将它们与新点p一起存储在点数组V中来实现的（第4-5行）。最近的点pnearest是通过比较V中每个点到中心pcenter的距离来获得的（第6行）。然后删除CD中的现有点（第7行），然后将最近的点pnearest插入k-d树（第8行）。框式搜寻的实现类似于第V-C2节中介绍的框式删除。
ikd-Tree上的点插入（第11-24行）是递归实现的。该算法从根节点开始向下搜索，直到找到一个空节点以追加一个新节点（第12-14行）。新叶节点的属性初始化为表1。在每个非空节点上，新的点与存储在树节点上的点沿分割轴进行比较，以便进一步递归（第15-20行）。这些被访问过的节点的属性（例如，treesize、range）用第V-C3节中介绍的最新信息（第21行）进行更新。算法检查并维护用新点更新的子树的平衡标准，以保持ikd-Tree（第22行）的平衡特性，详见第V-D节。
表1 要插入的新树节点的属性初始化
2)使用懒惰标签进行框式删除：在删除操作中，我们使用了惰性删除策略。也就是说，这些点不会立即从树中删除，而只是通过将属性detected置为true来将点标记为“已删除”（参见Data Structure，第6行）。如果以节点T为根的子树上的所有节点都已被删除，则T的属性treedeleted被设置为true。因此detected和treedeleted的属性称为惰性标签。标记为“已删除”的点将在重建过程中从树中删除（参见第V-D节）。
框式删除是利用属性range中的范围信息和树节点上的惰性标签实现的。如V-B中所述，属性range由外接长方体CT表示。伪代码如算法3所示。
给定要从以T为根的（子）树中删除的长方体CO，该算法递归搜索树并将外接长方体CT与给定的长方体CO进行比较。如果CT和CO之间没有交集，递归直接返回而不更新树（第2行）。如果外接长方体CT完全包含在给定的长方体CO中，则框式删除将属性detected和treedeleted都置为真（第5行）。当（子）树上的所有点都被删除时，属性invalidnum等于treesize（第6行）。对于CT与CO相交但不包含在CO中的情况，如果当前点p包含在CO中，则首先将其从树中删除（第9行），然后算法递归查找子节点（第10-11行）。当前节点T的属性更新和平衡维护在框式删除操作之后进行（第12-13行）。
3)属性更新：在每次增量操作后，使用AttributeUpdate函数，用最新的信息更新被访问节点的属性。该函数通过汇总其两个子节点上的对应属性和自身的点信息来计算属性treesize和invalidnum；通过合并两个子节点的范围信息和存储在其上的点信息来确定属性range；如果两个子节点的treedeleted都为真，并且节点本身将被删除，则treedeleted被设置为真。
D.重平衡
ikd-Tree会在每次增量操作后主动监控balance特性，并通过仅重新构建相关子树来动态地重平衡自身。
1)平衡准则：平衡准则由两个子准则组成：α-平衡准则和α-删除准则。假设ikd-Tree的一个子树以T为根。当且仅当它满足以下条件时，该子树是α-平衡的：
其中
，S(T)是节点T的treesize属性。
以T为根的一个子树的α-删除准则是：
其中
，I(T)表示子树上无效节点的数量（即节点T的属性invalidnum）。
如果ikd-Tree的一个子树同时满足这两个准则，则该子树是平衡的。如果所有子树都是平衡的，则整个树是平衡的。违反任一准则将触发重建过程以重新平衡该子树：α-平衡准则保持树的最大高度。很容易证明，α-平衡树的最大高度是
，其中n是树的大小；α-删除准则确保删除子树上的无效节点（即，标记为“已删除”）以减小树的大小。降低k-d树的高度和大小允许在未来进行高效的增量操作和查询。
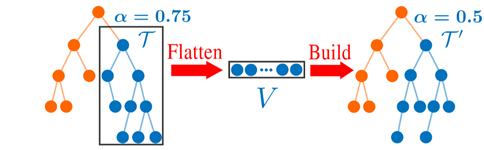
2）重建和并行重建：假设在子树T上触发重建（见图4），首先将子树展平为点存储阵列V。标记为“已删除”的树节点在展平期间被丢弃。然后如第V-B节所述，用V中所有的点构建一个新的完美平衡的k-d树。当在ikd-Tree上重新构建大型子树时，可能会出现相当大的延迟并破坏FAST-LIO2的实时性能。为了保持较高的实时性，我们设计了一种双线程重建方法。我们提出的方法不是简单地在第二个线程中重新构建，而是通过一个操作记录器避免两个线程中的信息丢失和内存冲突，从而始终保持k-最近邻搜索的完全准确性。
图4 重建一个不平衡的子树
广告
最新资讯
-
国际电工委员会/电动道路车辆和工业卡车电
2024-05-14 10:10
-
整车下线检测：AVM标定
2024-05-13 14:02
-
大模型技术专栏—5分钟搭建SpringAI大模型
2024-05-13 13:32
-
整车下线检测：ADAS标定
2024-05-13 13:30
-
浪漫520，海克斯康2024“世界计量日”主题
2024-05-13 12:19
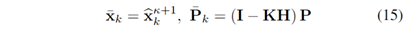
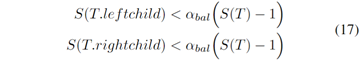
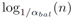
广告
广告
