广告
FAST-LIO2: 快速直接的激光雷达-惯性里程计
2021-09-12 21:53:49· 来源：同济智能汽车研究所
重建方法如算法4所示。当违反平衡准则且子树的树大小小于预定值Nmax时，子树将在主线程中被重建；否则，子树在第二个线程中被重新构建。第二个线程上的重建算法如函数ParRebuild所示。将第二个线程中要重建的子树表示为Г，将其根节点表示为T。第二个线程将锁定所有增量更新（即点插入和删除），但不查询该子树（第12行）。然后，第二个线程将包含在子树Г中的所有有效点复制到点数组V中（即，展平），同时保持原始子树不变，以便在重建过程中进行可能的查询（第13行）。展平后，原始子树被解锁，以便主线程接受进一步的增量更新请求(第14行)。这些请求将同时被记录在一个名为操作记录器的队列中。一旦第二个线程完成了从点数组V构建一个新的平衡k-d树Г'的这一过程（第15行），记录的更新请求将通过函数IncrementalUpdates（第16-18行）在Г'上再次执行。请注意，当并行重建开关已经在第二个线程中时，它会被设置为false。在所有待处理的请求被处理后，原始子树Г上的点信息与新子树Г'上的点信息完全相同，除了新子树的树结构比原始子树更加平衡。该算法从增量更新和查询中锁定节点T，并将其替换为新的T'（第20-22行）。最后，该算法释放原始子树的内存（第23行）。这种设计确保了在第二个线程的重建过程中，主线程中的建图过程仍然以里程计频率进行，而没有任何的中断，尽管此时的效率由于暂时不平衡的k-d树结构变得较低。需要注意的是，LockUpdates函数不会阻碍查询，查询可以在主线程中并行进行。相比之下，LockAl函数会阻止所有访问，包括查询，但它完成得非常快（即，只有一条指令），从而允许在主线程中进行及时查询。函数LockUpdates和LockAll是通过互斥（mutex）方式实现的。
E. K-最近邻搜索
尽管与那些著名的k-d树库[43]-[45]中的现有实例有些类似，但最近临搜索算法在ikd-Tree上被彻底优化。使用[41]中详述的“bounds-overlap-ball”测试，可以很好地利用树节点上的距离信息来加速最近邻搜索。我们维护一个优先级队列q来存储迄今为止遇到的k个最近的邻居以及它们到目标点的距离。当从树的根节点递归向下搜索树时，算法首先计算从目标点到树节点长方体CT的最小距离dmin。如果最小距离dmin不小于q中的最大距离，则无需处理该节点及其后代节点。此外，在 FAST-LIO2（和许多其他激光雷达里程计）中，只有当相邻点在目标点周围的给定阈值内时，它才会被视为内联点，并被用于状态估计，这自然为k最近邻的远程搜索提供了最大搜索距离[43]。在任何一种情况下，远程搜索都会通过将dmin与最大距离进行比较来删减算法，从而减少回溯量以提高时间性能。需要注意的是，我们的ikd-Tree支持多线程 k-近邻搜索并行计算架构。
F. 时间复杂度分析
ikd-Tree的时间复杂度可分为增量操作（插入和删除）、重建和k-最近邻搜索的时间。请注意，所有分析都是在低维度的假设下提供的（例如，FAST-LIO2 中的三个维度）。
1）增量操作：由于树上的下采样的插入依赖于框式删除和框式搜索，所以我们首先讨论框式的操作。假设n表示ikd-Tree的树大小，ikd-Tree上框式操作的时间复杂度为：
引理1. 假设ikd-Tree上的点在3-d空间Sx×Sy×Sz中，操作长方体为 CD = Lx×Ly×Lz。用长方体CD实施算法3的框式删除和搜索的时间复杂度为：
a,b,c≥0.∆min,∆med和∆max分别是a、b、c中的最小值、中值和最大值。α(u)，u∈[0,1]是flajolet-puech函数，其中提供了特定值：α(1/3)=0.7162和α(2/3)=0.3949。
证明：[56]中提供了k-d树上轴对齐超立方体范围搜索的渐近时间复杂度。除了懒惰标签附加到树节点之外，框式删除可以被视为范围搜索，这是O(1)。因此，范围搜索的结论可以应用于ikd-Tree上的框式删除和搜索，这产生了O(H(n))。
树上的下采样插入的时间复杂度为：
引理2. 在ikd-Tree上的算法2中使用树上的下采样的点插入的时间复杂度为O(logn)。
证明。ikd-Tree上的下采样方法由框式搜索和点插入后的删除组成。通过应用引理1，下采样的时间复杂度为O(H(n))。通常，下采样立方体CD与整个空间相比非常小。因此，归一化范围Δx、Δy和Δz很小，Δmin的值满足时间复杂度为O(logn)的条件(*)
ikd-Tree的最大高度可以很容易地从方程(17)中证明为
。而静态k-d树的值为log2n。因此引理直接从[40]中获得，其中k-d树上点插入的时间复杂度被证明为O(logn)。总结下采样和插入的时间复杂度得出结论，使用树上的下采样的点插入的时间复杂度为O(logn)。
2）重建：重建的时间复杂度分为单线程重建和并行双线程重建两种。在前一种情况下，重建是由主线程递归执行的。每个级别都花费排序时间（即O(n)），当维度k较低时，logn级别上的总时间为O(nlogn)[40]。对于并行重建，主线程消耗的时间只是扁平化（这使得主线程暂停进一步增量更新，算法4，第12-14行）和树更新（需要恒定时间O(1)，算法4，第20-22行）但没有构建（由第二个线程并行执行，算法4，第15-18行），拥有的时间复杂度为O(n)（从主线程看）。总之，重建ikd-Tree的时间复杂度对于双线程并行重建为O(n)，对于单线程重建为O(nlogn)。
3）K-最近邻搜索：由于ikd-Tree的最大高度保持不大于
，其中n为树的大小，从根节点向下搜索到叶子节点的时间复杂度为O(logn)。在树上搜索k最近邻的过程中，回溯的次数与常数成正比，该常数与树的大小无关[41]。因此，在ikd-Tree上获得k最近邻的预期时间复杂度为O(logn)。
6 基准实验结果
在此部分中，我们在各种开放数据集上进行了准确性、鲁棒性和计算效率方面的大量实验。我们首先对比其他数据结构，评估了我们的数据结构ikd-树，在18个不同大小的数据集序列上进行了kNN搜索。然后在VI-C部分，我们比较了FAST-LIO2在19个序列上的准确性和处理时间。所有序列都是从固态激光雷达[15]和旋转激光雷达收集的5个不同数据集中选择的。第一个数据集来自LILI-OM[17]，由固态3D激光雷达LivoxHorizon4收集，它具有非重复扫描模式和81.7°（水平）×25.1°（垂直）视场，典型的扫描频率为10赫兹，第一个数据集简称lili。陀螺仪和加速度计测量值由6轴XsensMTi-670IMU以200Hz的频率采样。数据是在具有结构化场景的大学校园和城市街道中记录的。第二个数据集来自MIT校园的LIO-SAM[30]，包含由以10Hz采样的VLP-16激光雷达5和以1000Hz采样的MicroStrain3DM-GX5-259轴IMU收集的多个序列，第三个数据集简称为liosam。它包含不同类型的场景，包括校园内的结构化建筑和森林。第三个数据集“utbm”[57]由最高达50公里/小时速度的有人驾驶机器车收集，该车具有两个10HzVelodyneHDL-32E激光雷达和100HzXsensMTi-28A53G25IMU。在本文中，我们只考虑左侧的激光雷达。第四个数据集“ulhk”[58]包含来自VelodyneHDL-32E的10Hz激光雷达数据和来自9轴XsensMTi-10IMU的100HzIMU数据。来自utbm和ulhk的所有序列都是由有人驾驶车辆在结构化的城市区域中收集的，而ulhk也包含许多移动车辆。最后一个数据集“nclt”[59]，是在密歇根大学北校区收集的大规模、长期的自主UGV（无人地面车辆）数据集。nclt数据集包含来自VelodyneHDL-32E激光雷达的10Hz数据和来自MicrostrainMS25IMU的50Hz数据。与其他数据集相比，nclt数据集的持续时间和数据量要长得多，并且包含多个开放场景，例如大型开放停车场。包括传感器类型和数据速率在内的数据集信息总结在表2中。这部分中使用的所有37个序列的详细信息，包括名称、持续时间和距离记录在附录A的表8中。
表2 基准测试数据集
为了让LIO-SAM能工作，nclt数据集中的IMU频率通过零阶插值从50Hz增加到100Hz
A.实现过程
我们在C++和机器人操作系统(ROS)中实现了提出的FAST-LIO2系统。迭代卡尔曼滤波器是基于我们之前工作[55]中介绍的IKFOM工具箱实现的。在默认配置中，局部地图大小L选择为1000m，激光雷达原始点在1:4（四个激光雷达点之一）时间下采样后直接用于状态估计。此外，所有实验的空间下采样分辨率（见算法2）均设置为l=0.5m。ikd-树的参数设置为αbal=0.6，αdel=0.5，Nmax=1500。基准比较的计算平台是轻量级无人机机载计算机：DJIManifold2-C，它有1.8GHz四核Inteli7-8550UCPU和8GB内存。对于FAST-LIO2，我们还在ARM处理器上对其进行了测试，该处理器通常用于降低功耗和成本的嵌入式系统。ARM平台是KhadasVIM3，它具有低功耗2.2GHz四核Cortex-A73CPU和4GBRAM，以关键字“ARM”表示。我们将“FAST-LIO2(ARM)”表示为FAST-LIO2在基于ARM的平台上的实现。
B.数据结构评估
1)评估设置：我们选择了动态数据结构的三个最先进的实现来与我们的ikd-树进行比较：R*-树[60]的boost几何库实现、oc树[61]的点云库实现和nanoflann[54]动态k-d树的实现。之所以选择这些树型数据结构实现，是因为它们的实现效率高。此外，它们支持动态操作（即点插入、删除）和范围（或半径）搜索，这对于与FAST-LIO2集成并对ikd-树进行公平的比较是十分必要的。对于地图下采样，由于其他数据结构不支持像ikd-树那样的树上的下采样，因此我们应用了与V-C中详述类似的方法，利用它们的范围搜索（对于八叉树和R*树）或半径搜索的能力（对于nanoflannkd树）。更具体地说，对于八叉树和R*-树，它们的范围搜索直接返回目标长方体CD内的点（参见算法2）。对于nanoflannk-d树，目标长方体CD首先被分成小立方体，其边长等于长方体的最小边长。然后通过半径搜索得到每个小立方体外接圆内的点，然后通过线性方法过滤掉长方体外的点，而保留目标长方体CD内的点。最后，与算法2类似，将CD中除距离中心最近的点以外的点从地图中移除。对于地图移动所需的框式删除操作（见第V-A部分），是根据各自的范围或半径搜索得到的点索引再将指定长方体内的点一一删除来实现的。
所有四种数据结构实现都会与FAST-LIO2集成，并在18个不同大小的序列上评估它们的时间性能。我们使用每个序列的每个数据结构运行FAST-LIO2，并记录kNN搜索、点插入（使用地图下采样）、由于地图移动导致的框式删除、新的一帧点云的点的数量和地图数量的时间每一步的点（即树的大小）。要查找的最近邻数量为5。
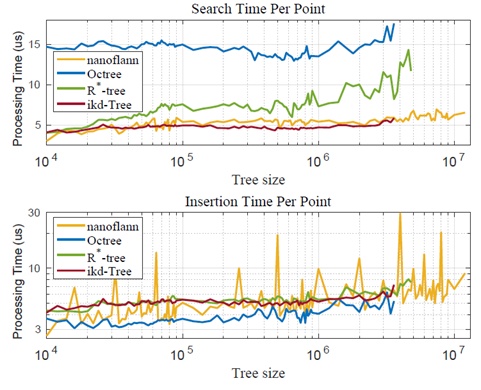
2）比较结果：我们首先比较所有18个序列中不同树大小的点插入（使用地图下采样）和kNN搜索消耗的时间。对于每个评估的树大小S，我们收集树大小在[S−5%S,S+5%S]范围内的处理时间以获得足够数量的样本。图5显示了每个单个目标点的插入和kNN搜索的平均时间消耗。八叉树在点插入方面取得了最好的性能，虽然与另一个的差距很小（低于1μs），但由于树结构不平衡，它的查询时间要长得多。对于nanoflannk-d树，插入时间通常比ikd-树和R*-树略短，但由于其组织一系列k-d树的对数结构，偶尔会出现巨大的峰值。这样的峰值严重降低了实时能力，尤其是在维护大地图时。对于k-最近邻搜索，nanoflannk-d树比我们的ikd-树消耗更多的时间，尤其是当树的大小变大（105∼106）时。R*-树实现了与ikd-树相似的插入时间，但对于大树的搜索时间要长得多。最后我们可以看到用树上的下采样和ikd树kNN搜索的插入时间确实与logn成正比，这与第V-F节中的时间复杂度分析一致。
对于用于激光雷达里程计和制图的任何地图数据结构，地图查询（即kNN搜索）和增量地图更新（即由于地图移动而进行下采样和框删除的点插入）的总时间最终会影响实时能力。该总时间总结在表3中。可以看出，八叉树在大多数数据集中的增量更新中表现最好，紧随其后的是ikd-树和nanoflannk-d树。在kNN搜索中，ikd-树的性能最好，而ikd-树和nanoflannk-d树在很大程度上优于其他两个，这与过去的比较研究一致[42,43]。在所有其他数据结构中，ikd树实现了最佳的整体性能。
需要注意的是，虽然nanoflannk-d树实现了与ikd-树相似的性能，但插入时间峰有更为深刻的影响，并且它对激光雷达里程计和建图的影响是很严重的。Nanoflannk-d树删除一个点是仅通过掩蔽它，而不实际从树中删除它。因此，即使进行地图下采样和地图移动，删除的点仍会保留在树上，影响后续查询和插入性能。由此产生的树的大小比ikd-树和其他树增长得更快，从图5中也观察到了这一现象。对于短序列（ulhk和lili）的影响可能很小，但对于长序列（utbm和nclt）变得明显。Nanoflannk-d树的大小在utbm数据集中超过6×106，在nclt数据集中超过107，而ikd-树的最大树大小分别达到2×106和3.6×106。nanoflann增量更新的最大处理时间在七个utbm数据集中都超过3秒，在三个nclt数据集中超过7秒，而我们的ikd-树将最大处理时间保持在nclt_2中的214.4毫秒，其余17个序列中的最大处理时间小于150毫秒.虽然nanoflann的这种处理时间峰由于其发生率低而不会严重影响整体实时能力，但它会导致后续控制的灾难性延迟。
表3 每次扫描平均时间消耗在增量更新、KNN搜索和总时间上的比较
每次扫描增量更新的平均时间消耗，包括使用树上的下采样的点插入和框删除。
单线程kNN搜索每次扫描的平均时间消耗
图5 不同树大小的数据结构比较
C.精度评估
在本部分中，我们将FAST-LIO2整个系统与其他最先进的激光雷达-惯性里程计和建图系统进行比较，包括LILI-OM[17]、LIO-SAM[30]和LINS[31]。由于FAST-LIO2是一种没有任何环路检测或校正的里程计，为了公平比较，LILI-OM和LIO-SAM的环路闭合模块被停用，而所有其他功能如滑动窗口优化等所有功能都启用。我们还对FAST-LIO2进行了控制变量研究：为了了解地图大小的影响，除了默认的1000m之外，我们在2000m、800m、600m的各种地图尺寸L上运行算法；为了评估直接方法对基于特征的方法的有效性，我们从FAST-LIO[22]（针对固态激光雷达进行了优化）和BALM[20]（针对旋转激光雷达进行了优化）中添加了一个特征提取模块。结果以“Feature”为关键词报告。所有实验均在Manifold2-C平台（Intel）上进行。
我们对lili、lisam、utbm、ulhk和nclt全部五个数据集进行评估。由于并非所有序列都有地面实况（受天气、GPS质量等影响），我们从五个数据集中总共选择了19个序列。这19个序列要么具有良好的真实轨迹（如数据集作者所推荐），要么在起始位置结束。因此，我们计算和评估了绝对平移误差(RMSE)和端到端误差这两个标准。
1)RMSE基准：表4中对RMSE进行了计算和报告。可以看出，增加FAST-LIO2的地图大小会提高整体精度，因为当激光雷达重新访问以前的地方时，新的一帧点云的点会配准到较旧的历史点。当地图大小超过2000m时，精度增量不是持久的，因为里程计漂移可能导致与太旧的地图点可能出现错误点匹配，这是任何里程计的典型现象。此外，直接方法在大多数序列中优于FAST-LIO2基于特征的变体，除了在nclt_4和nclt_6这两个中的差异很小且可以忽略不计。这证明了直接法的有效性。
与其他LIO方法相比，FAST-LIO2或其变体在所有19个数据序列中的18个中取得了最佳性能，是所有实验中最稳健的LIO方法。唯一的例外是在ulhk_4上，LILI-OM的精度略高于FAST-LIO。值得注意的是，LILI-OM在utbm_9、nclt_4、nclt_6、nclt_8和nclt_10中显示出非常大的漂移。原因是它的滑动窗口后端融合（建图）随着地图点数量的增长而失效。因此，它的姿态估计仅依赖于快速累积漂移的前端里程计。LINS在nclt_5,nclt_6,nclt_7,nclt_10中的工作情况同样不好。LIO-SAM在nclt_4,nclt_10也表现出很大的漂移，这是由于后端因子图优化在很长时间和很长距离的数据下的失效。nclt_10序列的示例视频可以在https://youtu.be/2OvjGnxszf8上找到。此外，在LILI-OM、LIO-SAM和LINS可以正常工作的其他序列上，FAST-LIO2的性能仍然有很大的优势。最后，应该注意的是，序列liosam_1直接从LIO-SAM[30]中提取，因此该算法已针对数据进行了良好的调整。但是，FAST-LIO2仍然实现了更高的精度。
广告
广告
编辑推荐
最新资讯
-
燃料电池汽车防水淹控制策略-倾斜路面
2024-11-02 11:32
-
Applus Idiada推出先进的电池安全实验室
2024-11-02 09:48
-
超120亿！一汽车零部件项目落地苏州！
2024-11-02 09:46
-
测试基础｜汽车软件测试术语解释
2024-11-02 09:03
-
区域化配电的技术及趋势
2024-11-02 08:16
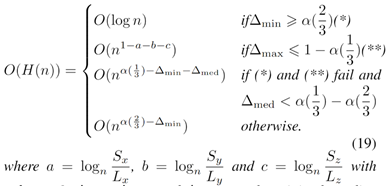
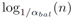
广告
广告
