广告
基于轮胎稳态和瞬态特性的车辆响应研究
2021-09-12 22:07:00· 来源：轮胎动力学协同创新联盟订阅号 作者：李雪莉
在整车动力学正向研究过程中，将用户要求转化为工程语言的整车技术规范（VTS），并分解为系统特性是车辆性能目标达成的关键，也是车辆生产的核心技术。轮胎作为
在整车动力学正向研究过程中，将用户要求转化为工程语言的整车技术规范（VTS），并分解为系统特性是车辆性能目标达成的关键，也是车辆生产的核心技术。轮胎作为整车动力学达标与否的关键部件[1]，其性能与控制主要依托于主观评价，随着正向开发流程的发展和完善，整车动力学VTS目标的量化使得轮胎客观指标的设定成为可能，可有效形成轮胎性能开发的主客观闭环。
目前，如何在概念阶段设计与实现轮胎客观指标，进行整车动力学性能综合与分解的迭代，从而使整车动力学性能达标是摆在仿真工程师面前的难题。本工作通过对轮胎稳态和瞬态特性研究，建立基于轮胎稳态和瞬态特性的三自由度车辆模型，揭示了轮胎特性与整车动力学性能的关系，为轮胎性能目标的控制与优化提供理论指导。
1 轮胎稳态和瞬态特性
1. 1轮胎力学特性主要参数
轮胎力学特性研究轮胎受力与运动状态之间的关系，其主要参数有输入参数和输出参数两类[2]。主要输入参数包括纵向滑移率（κ）、滚动速度（Ω）、侧偏角（α）、偏转角（ψ）、外倾角（γ）和垂向力（Fz），主要输出参数包括纵向力（Fx）、侧向力（Fy）、翻倾力矩（Mx）、滚动阻力矩（My）和回正力矩（Mz），其中与底盘动力学直接相关的是Fy和Mz，而Fx和Fz对Fy间接产生作用，进而影响车辆的运动。
1. 2轮胎稳态特性
1. 2. 1轮胎稳态刷子模型
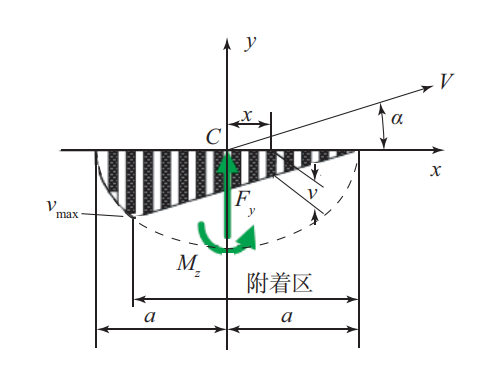
轮胎稳态刷子模型不考虑胎体变形[3]，将轮胎等效为刚性胎体和弹性胎面两部分。在纯侧偏工况下，轮胎接地印痕区内胎面单元变形如图1所示。图中，V为轮胎接地印痕区接地中心（C点）速度，a为半印痕长度，α为V与胎体中心基准线间的夹角，ν为印痕区微元速度，νmax为印痕区微元最大速度。
图1 纯侧偏工况下轮胎接地印痕区胎面单元变形示意
假设α输入无穷小或路面摩擦因数趋向无限大，可以认为整个接地印痕区都为附着区，胎面单元不发生滑移[4]。对接地印痕区积分，可得到Fy和Mz：
式中，qy（x）为侧向力分布函数。
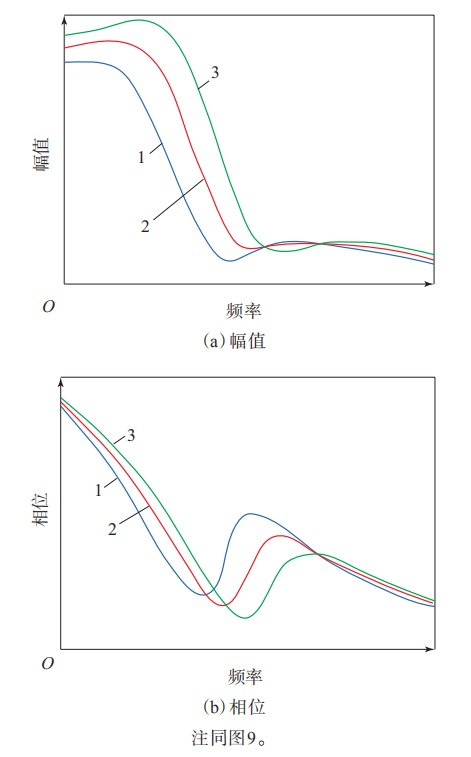
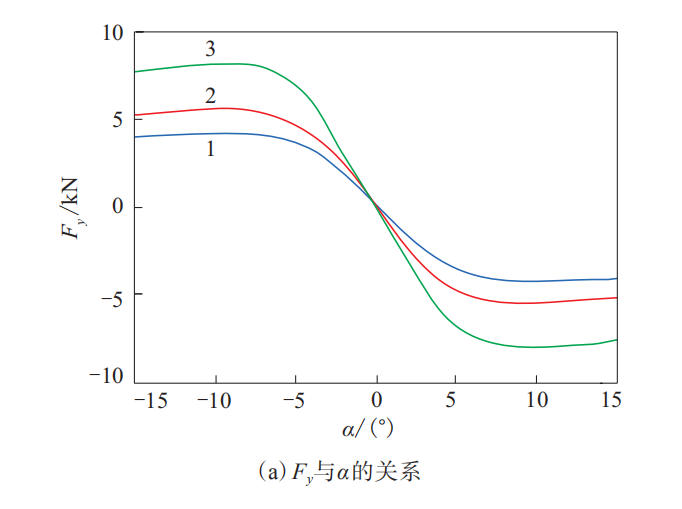
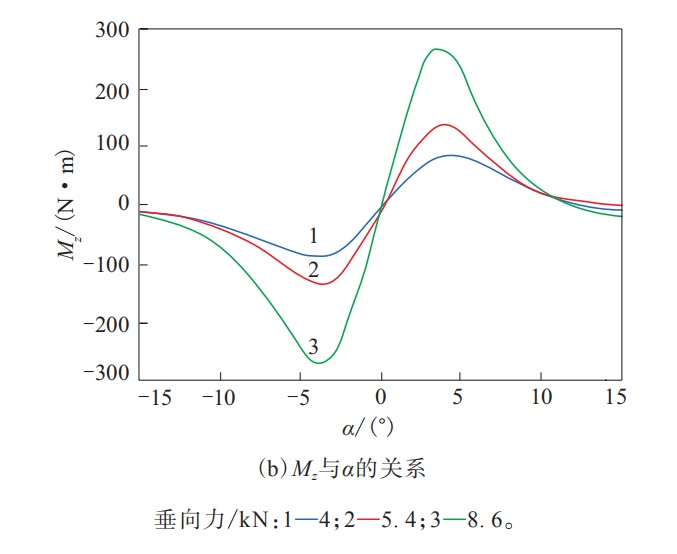
轮胎稳态刷子模型纯侧偏工况下Fy和Mz与α的关系如图2所示。
图2 轮胎稳态刷子模型纯侧偏工况下Fy和Mz与α的关系
1. 2. 2轮胎侧倾
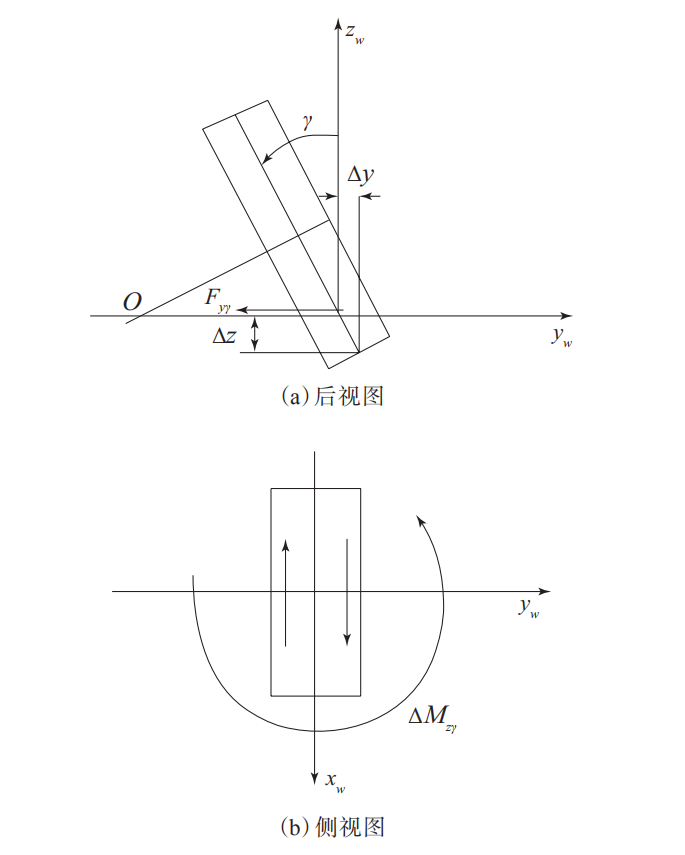
当车轮存在γ时（见图3），车轮会发生绕自身旋转轴线与地面交点滚动的趋势，在宽度方向可以把轮胎看作由无数个无厚度圆盘重叠而成。在轮胎中心平面内的圆盘在法向和侧向的变形分别为Δz和Δy。由于存在侧向变形，纯侧倾运动时会产生侧向力Fyγ和回正力矩Mzγ（下标γ指产生力的原因）。
图3 轮胎纯侧倾工况示意
广告 
广告
最新资讯
-
测迅乌镇&盐城测试场：助力智能网联汽车标
2025-02-22 12:39
-
使用示波器对三相电机驱动器进行测量
2025-02-22 12:37
-
上汽集团大乘用车重磅招聘
2025-02-22 12:25
-
GB/T 44173-2024对开门预警DOW的要求
2025-02-22 12:25
-
声音工程：像用PS一样编辑声音
2025-02-21 17:04
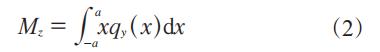
广告
广告
