广告
基于轮胎稳态和瞬态特性的车辆响应研究
2021-09-12 22:07:00· 来源：轮胎动力学协同创新联盟订阅号 作者：李雪莉
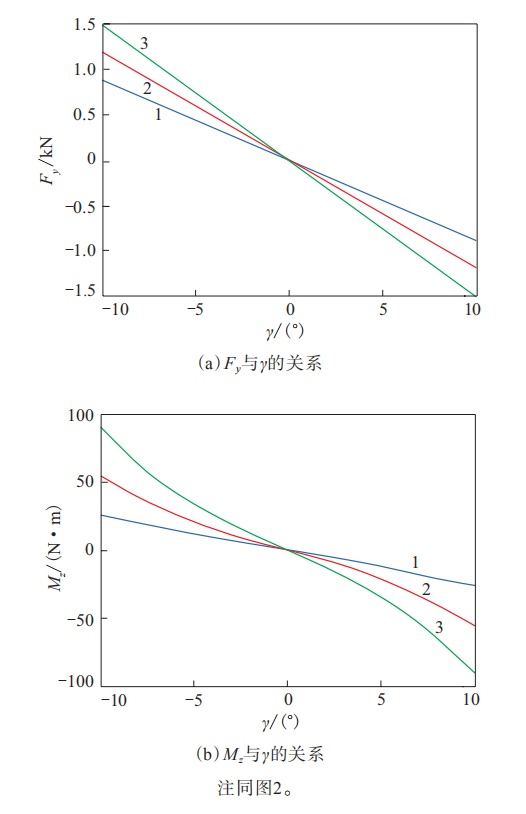
轮胎稳态刷子模型纯侧倾工况下Fy和Mz与γ的关系如图4所示。
图4 轮胎稳态刷子模型
纯侧倾工况下Fy和Mz与γ的关系
1. 3轮胎瞬态特性
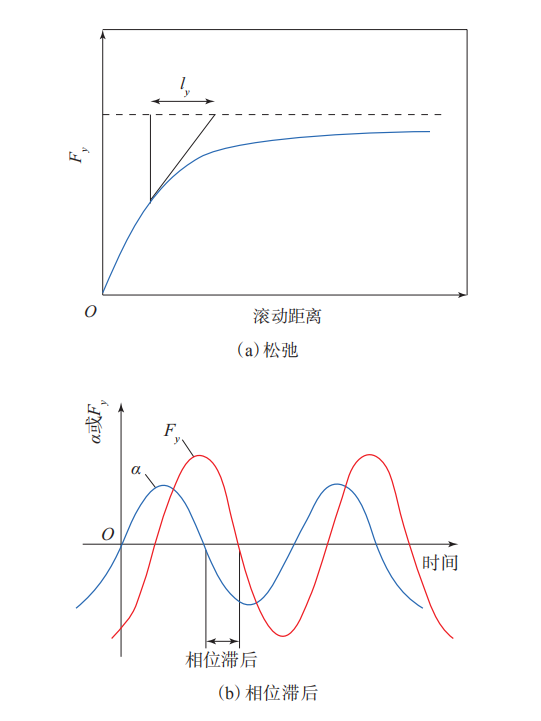
在稳态刷子模型中，轮胎的受力与运动状态直接相关，由于轮胎多在中低频下工作，轮胎与地面之间的力和力矩相对于轮胎的运动输入表现为一定的滞后，如图5所示。从图5可以看出：轮胎在α阶跃输入作用下需要滚动一段距离（ly）后，Fy才达到稳态值；在α正弦输入作用下Fy表现出相位滞后。该现象即为轮胎瞬态特性。
图5 轮胎瞬态特性
引入松弛的概念描述以上现象，根据理论推导[5-6]，Fy对α增量的频率响应特性近似于一阶系统，因此Fy瞬态模型可以用一阶松弛系统来近似表达。Fy瞬态松弛（HFy，α）模型可表达为：
式中，Kyα为轮胎侧偏刚度，σ为系数，s为频率复变量。当σs→0时，HFy，α→Kyα，即在低频时，侧向力幅频特性水平渐近线与一阶松弛系统水平渐近线相同。
通常轮胎松弛长度的获取有两种方法，一种为直接法，通过α阶跃法提取ly，另一种间接通过轮胎侧偏刚度与侧向刚度的比值得到。
2 三自由度车辆模型建立
二自由度车辆模型包括侧向和横摆两个自由度，在侧倾转向效应较小的情况下，可以得到较好的仿真效果。但是，在侧倾转向效应较大时，这样的简化模型就不够精确了。考虑侧倾自由度的转向盘角阶跃输入运动理论最早出现于1956年的美国康乃尔实验室，可以将高速、大转角和侧向加速度较大时的侧倾转向效应计入，大大提高了车辆模型的仿真精度[6]。
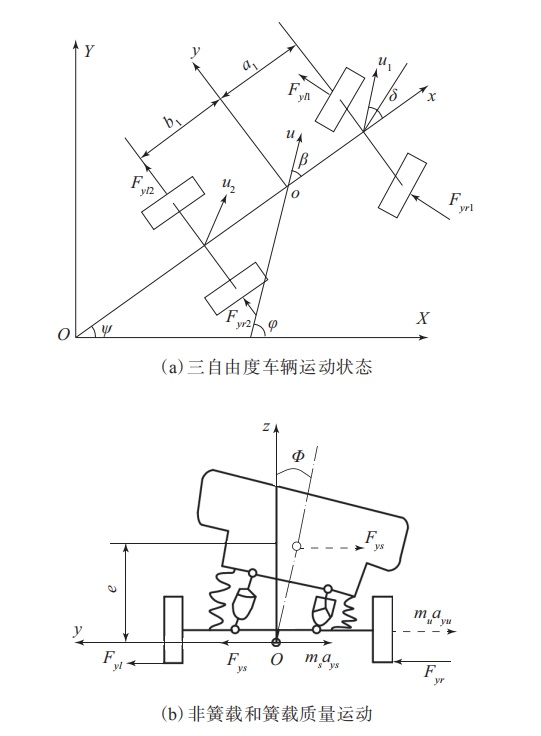
三自由度车辆模型在二自由度车辆模型的基础上增加了侧倾自由度，车辆运动状态如图6所示，非簧载质量参与横摆运动，簧载质量参与横摆运动（有横摆角速度）和侧倾运动（有侧倾角速度），忽略俯仰运动。若前后轴侧倾中心高相同，则横摆与侧倾解耦。图中，下标l和r分别表示车辆左侧和右侧，下标1和2分别表示车辆前轴和后轴，a1和b1分别为质心到前后轴的距离，u为车辆纵向速度，δ为车轮转角，β为质心侧偏角，φ为车身侧倾角，ms和mu分别为非簧载质量和簧载质量，Fys和Fyu分别为非簧载力和簧载力，ays和ayu分别为非簧载质量和簧载质量在y轴的加速度，e为质心高度，Φ为轮胎侧倾角。
图6 三自由度车辆模型
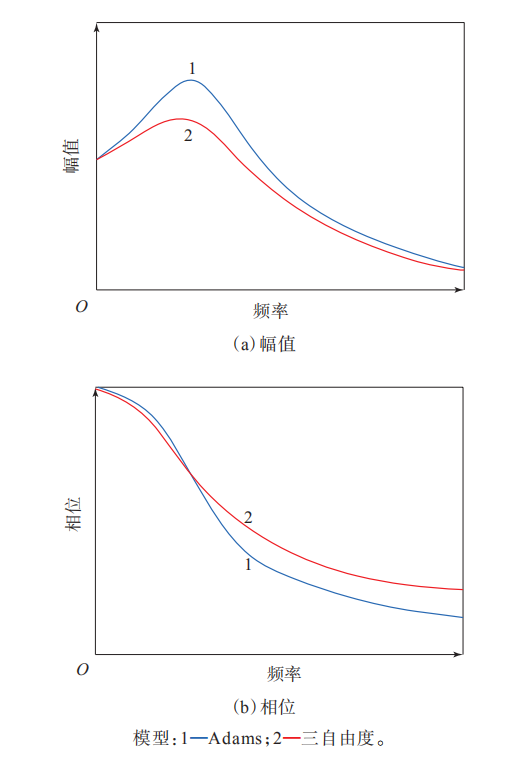
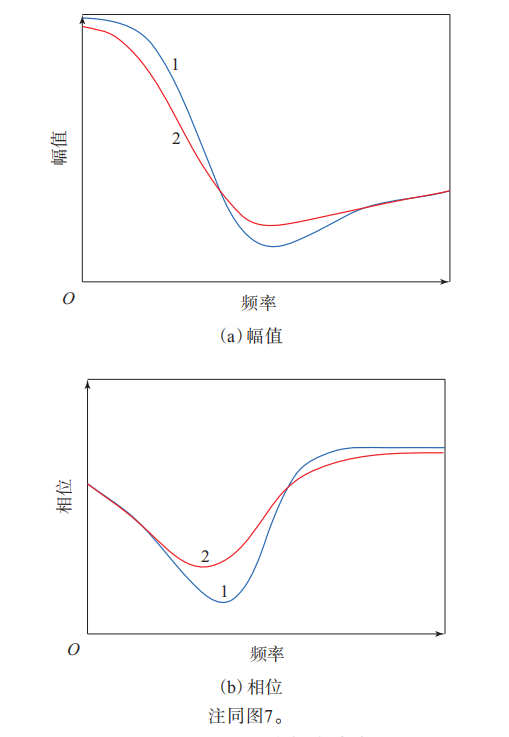
建立的三自由度车辆模型与机械系统动力学自动分析（Adams）车辆模型对比，三自由度车辆模型具有非常高的精度，可以用来研究轮胎特性对车辆响应的影响[7-8]，如图7和8所示。
图7 横摆角速度频率响应
图8 侧向加速度频率响应
3 轮胎特性参数对整车性能的影响
车辆三自由度侧倾研究以轮胎松弛模型为对象，车辆响应为目标，对轮胎的稳态和瞬态特性参数进行试验设计与分析。
3. 1轮胎稳态参数对整车性能的影响
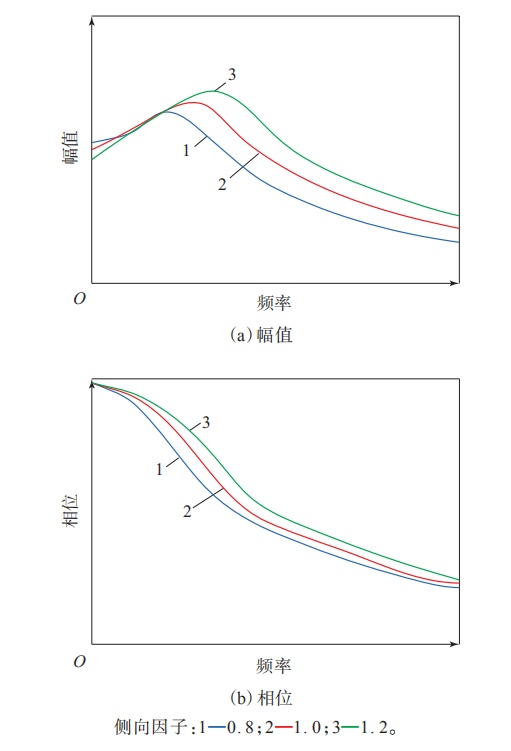
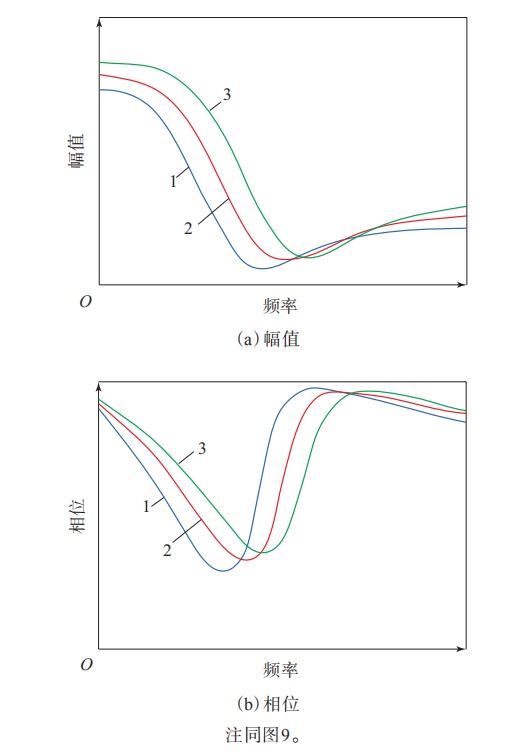
将轮胎侧偏刚度、侧倾刚度、回正刚度、侧倾回正刚度以及悬架运动学与动力学特性合成为等效侧偏刚度，进行归一化并等效为轮胎侧向因子，设计轮胎侧向因子分别为0. 8，1. 0和1. 2，进行试验设计与分析，得到轮胎侧向特性对整车响应的影响[9-10]，如图9—12所示。
图9 轮胎侧向因子对横摆角速度频率响应的影响
图10 轮胎侧向因子对侧向加速度频率响应的影响
广告 
广告
最新资讯
-
荷兰Zepp氢燃料电池卡车-Europa
2024-12-22 10:13
-
NCACFE -车队油耗经济性报告（2024版）
2024-12-22 10:11
-
R54法规对商用车轮胎的要求（上）
2024-12-22 10:10
-
蔚来ET9数字架构解析
2024-12-22 09:53
-
4G/5G网络新时代的高效紧急呼叫系统NG-eCal
2024-12-20 22:33
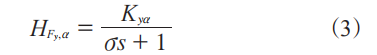
广告
广告
