广告
基于非线性扰动观测的商用车ESC自适应滑模控制研究
2021-09-15 01:15:30· 来源：汽车制动之家
［摘要］针对商用车ESC控制中，实际车辆存在各种扰动，难以建立精确的车辆模型，传统滑模控制存在较大抖振等问题，本文中提出基于非线性扰动观测（NDOB）的自适
［摘要］针对商用车ESC控制中，实际车辆存在各种扰动，难以建立精确的车辆模型，传统滑模控制存在较大抖振等问题，本文中提出基于非线性扰动观测（NDOB）的自适应滑模控制（ADSMC）算法。首先，利用非线性扰动观测器对车辆建模的扰动项进行估计；然后，采用径向基神经网络对滑模控制器的关键参数进行自适应调节，以简化参数调节过程、减小滑模抖振、提高控制精度；最后，在TruckSim中建立车辆模型，在MATLAB中建立控制策略模型，在电控气压硬件在环试验台上，对控制算法进行试验验证。试验结果表明，NDOB-ADSMC算法的ESC控制效果良好，能够满足车辆ESC控制需求。
随着经济快速发展，商用车保有量快速增加。商用车与乘用车相比，具有质心高、质量大等特点，商用车在紧急情况下比乘用车更容易发生交通事故，因而目前对商用车主动安全控制的研究越来越受到重视。车辆电子稳定性控制系统（electronic stability controller，ESC）能够显著改善车辆的操纵性能，在极限行驶工况下，ESC能够防止车辆发生横摆失稳、侧翻失稳等危险情况。目前关于车辆ESC控制的研究，对乘用车的研究相对较深入，但对商用车的研究较少。
在商用车ESC控制中，建立一个准确的车辆模型是进行精确控制的前提条件，但在实际ESC控制中，车辆建模常存在如下原因，造成系统不确定性：模型简化、参数摄动、未知的外界干扰等。如果将不精确的车辆模型应用到ESC控制中，轻则影响控制精度，重则控制发散。轮胎侧偏刚度在车辆实际运行过程中，随着车辆行驶状态而变化，文献［2］中将实际轮胎侧偏刚度扰动值表示为一个与有界扰动和侧偏刚度偏差的函数，设计了针对非线性系统的最优控制器，综合评估了不同的侧偏刚度偏差值对车辆动态性能的影响，从而在实际控制中，选择一个最优的侧偏刚度偏差值。文献［3］～文献［6］中在制动防抱死控制中，考虑系统的不确定性，将系统所有的不确定项合并成一项，设计复杂的神经网络控制器对系统的非线性不确定项进行估计。文献［7］中建立2自由度车辆模型，考虑前后轴等效侧偏刚度的参数摄动、外界扰动，利用径向基神经网络对这些扰动进行估计。
目前关于车辆建模的不确定性，大多是通过复杂的神经网络对不确定项进行估算，由于实际的车辆模型高度复杂且非线性，故计算量大，给实际的工程应用带来了一定的难度。在车辆ESC控制中，滑模控制由于具有算法结构简单、响应速度快、对于外界干扰具有较强的鲁棒性等优点，故在实际工程中应用较多。但在滑模控制中，抖振现象是一个无法避免的问题，抖振会影响系统的控制精度。
为解决上述的问题，本文中基于商用车电控气压制动系统，提出了商用车ESC非线性扰动观测的自适应滑模算法（NDOB-ADSMC）。首先，建立2自由度车辆模型，对车辆系统不确定项提出了非线性扰动观测器，对车辆ESC控制提出了滑模控制算法。其次，进行Lyapunov有限时间稳定理论证明，结果表明非线性扰动观测器可有效减小滑模观测器的符号项系数，从而抑制滑模抖动，提高系统的控制精度。然后，为更进一步减小滑模控制的抖振、提高控制精度、优化滑模控制，本文中利用结构简单的RBF神经网络算法的自适应调节能力对传统SMC的指数项参数进行自适应调节。最后，在电控气压制动系统硬件在环试验台上对算法的有效性和控制精度进行试验验证。
1 2自由度车辆模型
建立如图1所示的2自由度车辆模型。
图1 整车动力学模型
最终可得2自由度车辆模型方程：
式中：β为车辆质心侧偏角；k f为前轴等效侧偏刚度；k r为后轴等效侧偏刚度；m为车辆质量；u为车辆纵向车速；a为前轴轴距；b为后轴轴距；ωr为车辆横摆角速度；δ为车辆前轮转角；Iz为车辆绕z轴的转动惯量。
在车辆ESC控制中，车辆横摆角速度和质心侧偏角是进行控制计算的关键参数。一般来说，理想横摆角速度可通过稳态横摆角速度增益来计算：
式中：L为车辆轴距；K为稳定性因数。
车辆在实际运动过程中，车辆的运动状态还要受路面附着系数因素的限制，车辆的最大侧向加速度需要满足如下条件：
在车辆实际的行驶过程中，车辆侧向加速度可近似表达为
由式（4）和式（5）计算可得
综上所述，可得理想横摆角速度：
在车辆的实际行驶过程中，一般车辆的质心侧偏角都比较小，在实际控制中，应尽可能减小车辆质心侧偏角，故在实际控制中，为简化计算，设定理想质心侧偏角为0。
2 ESC控制器
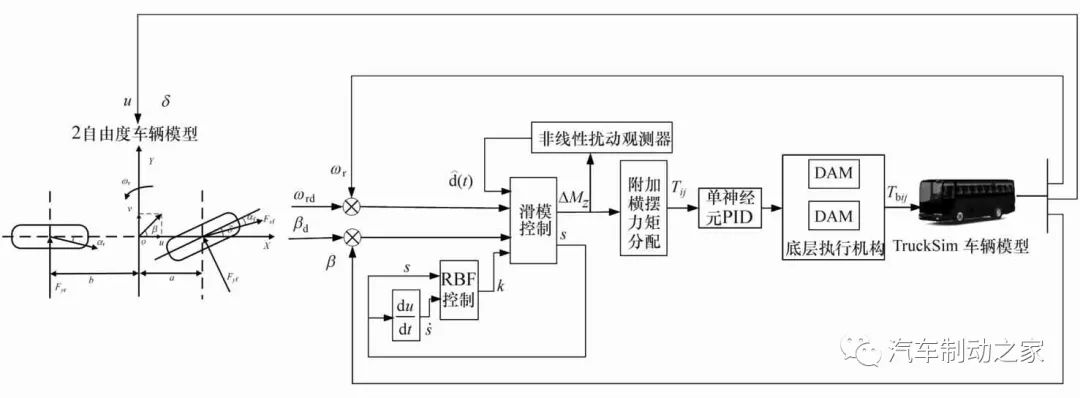
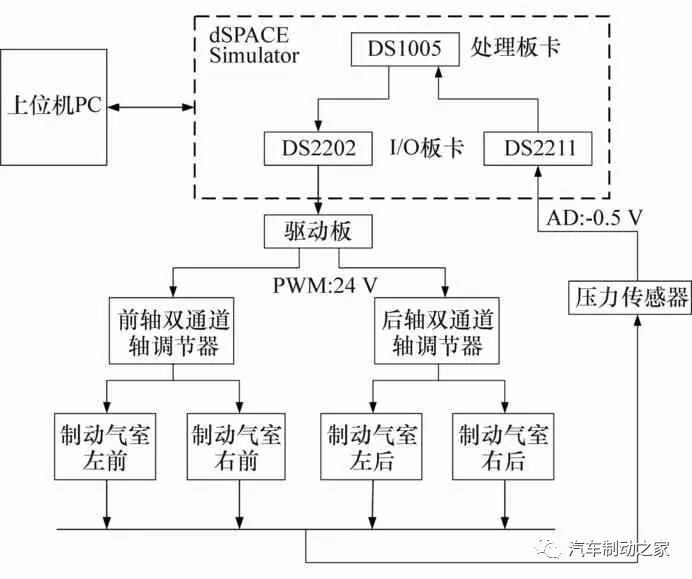
图2为本文中ESC控制架构，整个ESC控制包括两个部分：上层NDOB-ADSMC控制器和底层执行机构控制器。上层NDOB-ADSMC控制器包括滑模控制器、非线性扰动观测器和RBF神经网络控制器，底层执行机构采用单神经元PID控制。图2中DAM是底层的核心执行机构，为美国WABCO公司生产的双通道轴调节器。
图2 ESC控制框图
2.1 基于非线性扰动观测的附加横摆力矩控制器
在车辆实际行驶过程中，式（1）2自由度车辆模型中，k f、k r与车速、路面附着系数等各种因素相关，存在不确定的参数摄动，车辆建模过程中，为简化计算过程，忽略车辆悬架、转向、空气阻力等不确定因素，这些不确定性都可以归结为一个集成非线性扰动。当车辆失稳时，ESC控制器计算出保持车辆稳定所需的附加横摆力矩，可将式（1）表达为
式中：Δ1为侧向运动集成非线性扰动项，Δ1是有界的；Δ2为横摆运动集成非线性扰动项，Δ2是有界的；ΔMz为附加横摆力矩。
设计滑模面为
式中ξ为权衡系数。
对滑模函数求导可得
由式（17）可知集成非线性扰动项d（t）有界，存在 D＞0，使得｜d（t）｜≤D。
选择滑模趋近律为指数滑模趋近律：式中：k＞0；ε＞0。
由式（14）和式（18）可得附加横摆力矩控制器：
附加横摆力矩控制器由连续项和包含符号函数的不连续项两部分组成，其中不连续项中的符号项是引发滑模控制抖振的主要原因，一般为了减小抖振，须尽可能减小参数ε。现在证明系统式（14）在式（19）附加横摆力矩控制器控制下的Lyapunov有限时间稳定性，选择Lyapunov函数为
对Lyapunov函数进行求导可得
由式（21）可知，当ε≥D的时候，系统满足Lyapunov有限时间稳定性。
由式（19）和式（21）可得，当ε≥D时，系统在附加横摆控制器作用下，系统满足Lyapunov有限时间稳定性。但是D为 d（t）的上界，集成扰动d（t）中，包含有前后轴的等效侧偏刚度不确定项，一般数值比较大，从而导致选择的ε较大，最终会引发大的滑模控制抖振，抖振大时，会导致控制精度下降，执行机构频繁启动，严重时甚至会烧坏底层执行机构。为尽量减小滑模抖振，提高控制精度，本文中提出非线性扰动观测器对集成非线性扰动进行观测。将式（14）滑模函数改写为
根据非线性扰动观测器理论，对于式（24）有
式中
的估计值；L1为非线性扰动观测器的增益；P为非线性扰动观测器的内部状态。
定义扰动观测的估计偏差
广告 
广告
编辑推荐
最新资讯
-
荷兰Zepp氢燃料电池卡车-Europa
2024-12-22 10:13
-
NCACFE -车队油耗经济性报告（2024版）
2024-12-22 10:11
-
R54法规对商用车轮胎的要求（上）
2024-12-22 10:10
-
蔚来ET9数字架构解析
2024-12-22 09:53
-
4G/5G网络新时代的高效紧急呼叫系统NG-eCal
2024-12-20 22:33
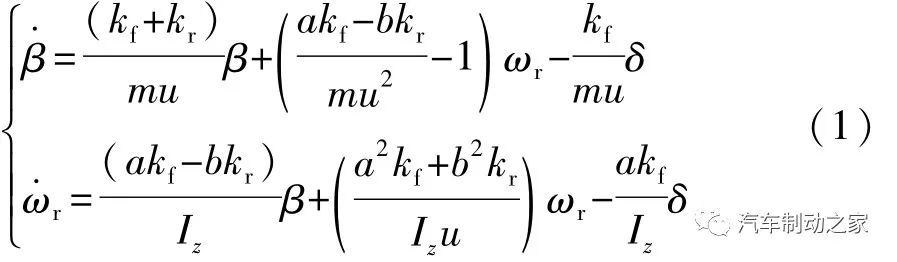
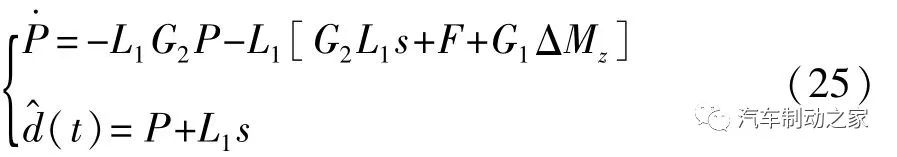
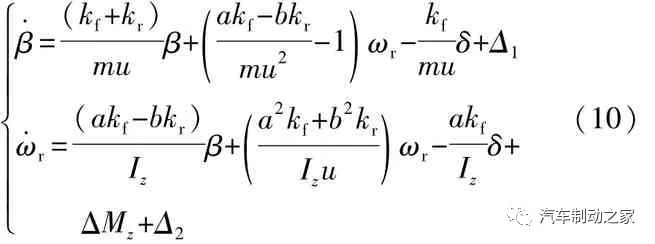
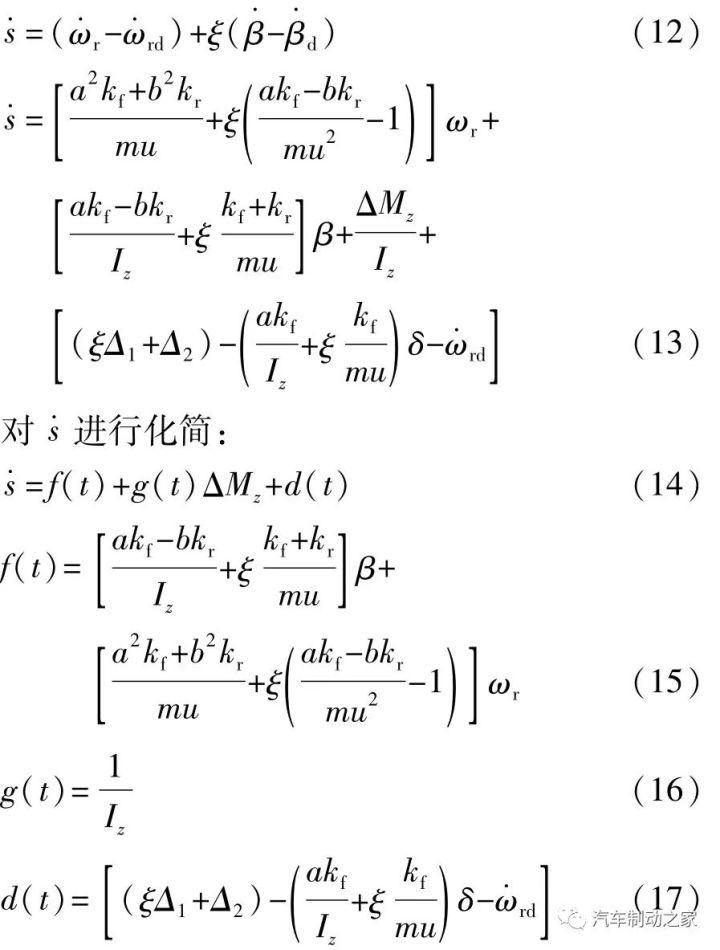
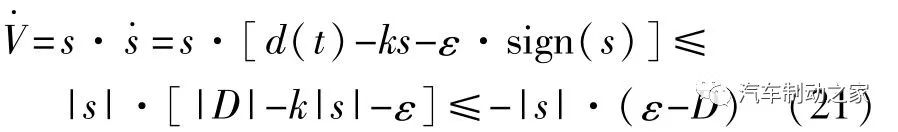
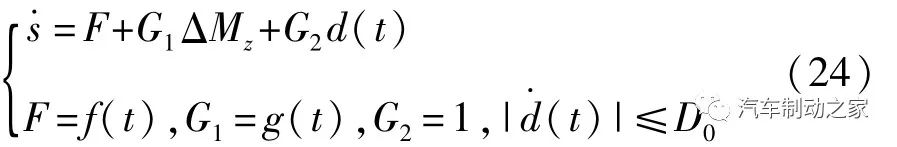
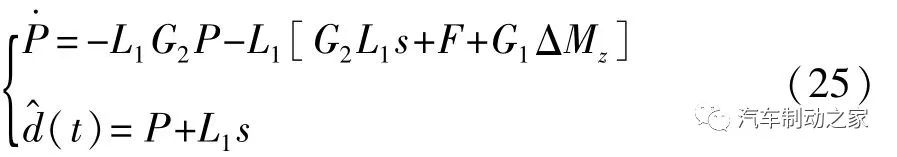
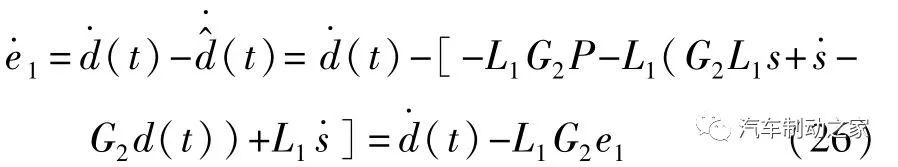
广告
广告
