广告
声品质客观指标概述——声音的调制（上）
2021-09-22 19:40:21· 来源：NVH老枪
本篇将与大家讨论调制指标在工程问题中的相关应用。调制指标是对声音幅值随时间变化的一种衡量，即基于人类的听觉感受，判定人们对于调制声音的感知状态。例如在
本篇将与大家讨论调制指标在工程问题中的相关应用。调制指标是对声音幅值随时间变化的一种衡量，即基于人类的听觉感受，判定人们对于调制声音的感知状态。例如在工程中，我们可以应用调制指标，对排气系统的隆隆声，或是电动马达的拖拽声等现象进行相关评价，判定其对人类听觉主观感受的影响。
——3#老枪
在上一篇关于语言清晰度的文章中，为大家展示了如何应用语言清晰度指标，来衡量背景噪声或环境噪声对人类正常交谈的侵扰程度。本篇将继续声品质客观指标的话题，分上、下两篇来介绍NVH中的调制现象以及与调制相关的声品质分析指标的应用，同样希望能够给大家日常的声品质及NVH故障诊断工作，带来一定的帮助与启发。
上篇将首先介绍调制现象产生的机理，下篇将主要介绍调制现象的分析手段和方法。
对于NVH工程诊断中常见的调制现象，通常有两类，一类是由于旋转机械运转过程中的一些故障，所造成的幅值调制；另一类是两个频率相近的信号所造成的拍频现象，而表现出来的幅值调制。下面我们将分别就这两类调制现象产生的机理进行阐述。
1 旋转机械的幅值调制
讨论NVH工程诊断中的声音调制之前，首先我们先来聊一聊信号处理中的信号调制。所谓调制指的是信号的强度（整体幅值）随着时间的推移产生周期性的变化，在时域上实际上是一个低频信号对高频信号某一特征参量进行的控制。其中低频信号称为调制信号，高频信号称之为载波信号，而调制出来的信号则称之为已调载波。
所以，所谓调制过程，在时域上就是载波的某一特征参量随调制信号的变化而变化的过程，而在频域上则表现为移频的过程。而调制的类型有很多种，根据被调制的特征参量不同可分为：幅值调制、频率调制和相位调制。
在NVH工程问题中，我们常见的噪声问题以声音的幅值调制为主，即用低频的调制信号来改变高频的载波信号幅值。例如齿轮啮合过程中齿轮所在轴的转频被作为调制信号，对齿轮副啮合所产生的噪声信号产生调制。下面我们就来对这种幅值调制情况进行更为深入的分析。
首先，我们需要清楚幅值调制信号，实际上就是调制信号与载波信号在时域上的乘积；而转换到频域，根据傅里叶变换理论则是两个信号的卷积。其过程在数学上可以理解为三角函数的积化和差过程。下面进行简单的推导：
假设存在两个信号，分别为高频载波信号（如齿轮副的啮合频率， ）与低频调制信号（如某齿轮所在轴的转频， ），其表达式如下：
利用三角函数积化和差可得：
其中， 上面这个表达式便是已调信号。通过分析我们可以发现，载波信号通过与调制信号在时域上的相乘，其频率发生变化，对于载波信号而言，由原来的一个频率 变成了其附近的两个频率——载波信号频率与调制信号频率和与差 。由于调制信号频率一般远小于载波信号频率，故两个频率相差不大，所以才会造成傅里叶变换后产生两个边频的现象。下面我们以一个实例进行更为直观的分析。
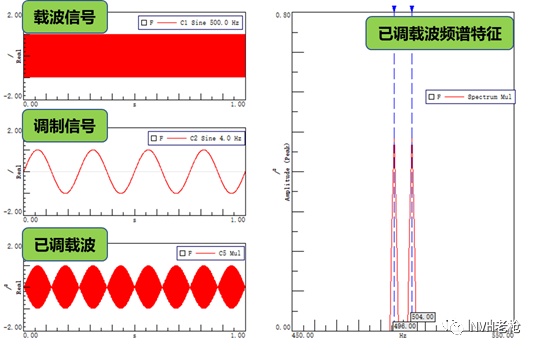
首先我们假设载波信号为一个500Hz的正弦波，其表达式为 ；调制信号为一个4Hz的正弦波，其表达式为 。将两个信号时域相乘，从而得到已调载波（如图1所示）：
图1 500Hz载波信号被4Hz调制信号进行调制后的时域及频域分析结果
从图中我们可以发现：首先，载波信号被调制信号调制后其幅值发生了明显变化，整体幅值呈现了周期性的上升和下降过程；其次，已调载波的频谱特征表现为两个频率相差不大的边频特征且其幅值降为0.5；最后，我们可以注意到，已调载波的整体幅值在1秒内变化了8次。
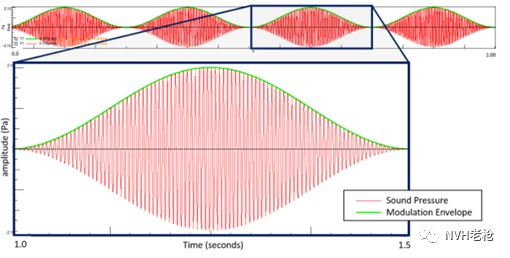
已调载波在1秒内整体幅值的变化次数，我们称之为调制频率，那所谓的整体幅值变化又该如何理解呢？下面通过对图2进行分析，便于我们更好的理解幅值调制中的调制频率这一个概念。
图2 调制信号及包络曲线
这里的声压级（红色曲线）变化非常快，在一秒钟内要变化上百次。红色的声压级曲线是由麦克风实际测量的，相当于施加在人类耳膜上的压力。声压同样存一种较慢的变化（绿色曲线）。该曲线并不是一个直接测量的量。这种缓慢变化的现象同样可以被听众感知到，这种变化即为幅值的整体变化，它类似于在音响上播放一首快节奏的歌曲，而音量旋钮随着时间的推移慢慢被调高和调低。这导致了人们对声音随时间变化的感知（绿色曲线）比声压信号的实际频率内容（红色曲线）慢得多。而这种缓慢变化的快慢程度我便用调制频率来衡量。（注：绿色曲线即为红色曲线的包络信号）
那么问题就来了：案例中用4Hz的正弦信号调制500Hz载波信号得到的已调载波的调制频率为8Hz，这一结论与我们平时的工程经验完全不一致。我们通常认为某一调制信号调制载波信号后其问题噪声的调制频率即为调制信号频率，例如：齿轮啮合过程中齿轮所在轴的转频作为调制信号，调制齿轮副啮合所产生的噪声信号时，其问题噪声的调制频率即为齿轮所在轴的转频。那问题出在哪里呢？
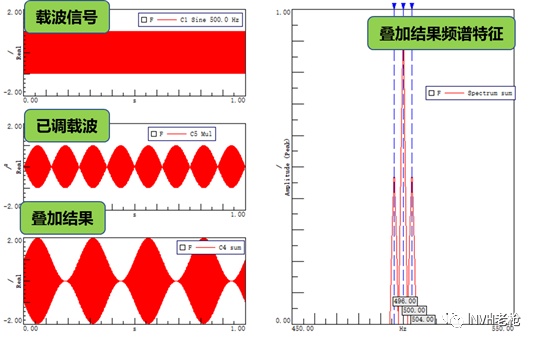
其实很简单，这主要是由于在NVH工程问题中，发生调制后原有的载波信号不可能消失，而是一直存在的，所以最终的问题噪声实际上是已调载波与载波信号在时域上再次发生叠加的结果。那我们回到上述案例分析，将已调载波上再次叠加500Hz的正弦信号，其分析结果如图3所示：
图3 已调载波叠加原始载波信号的分析结果
从图中我们可以发现，在叠加原始载波信号后其信号整体幅值呈现每秒中4次的变化，调制频率变为4Hz，与我们的工程经验一致。同时叠加结果的频谱特征中出现了载波信号的频率信息，呈现为中心频率+边频的特征，同样与我们的工程经验相吻合。
所以，在NVH工程诊断中，声音的幅值调制问题实际上是调制信号在时域上与载波信号相乘，再叠加原载波信号的结果。其表达式为：
2 声音的拍频现象
在工程实际中还存在一种与上述幅值调制现象类似的现象，就是当两个幅值相似且频率相近（但不相同）的单频声同时存在时，其合成的信号振幅也会随时间缓慢发生变化，产生类似打“拍”子的感觉。这种情况同样会严重影响听众的主观感受。我们称这种现象为拍频。
下面我们以一个实例来说明拍频现象是如何发生的：
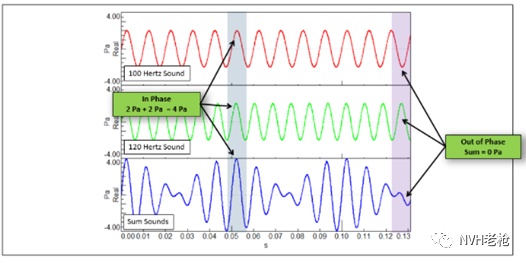
图4 100Hz单频声与120Hz单频声同时播放，发生幅值调制现象
如图4所示，存在一个100Hz纯音及一个120Hz纯音（振幅均为2Pa），同时播放二者（即时域相加），其合成信号的幅值在0~4Pa之间周期性变化，这种现象便称之为拍频。所以拍频现象同样表现为合成信号的整体幅值在时域内呈现周期性变化，但是其形成机理与幅值调制存在着本质的区别。
拍频现象是两个幅值相似、频率相近的正弦信号（也可以是多个正弦信号）在时域的相加，其过程为三角函数的和差化积，而幅值调制为调制信号与载波信号在时域内的相乘，其过程为三角函数的积化和差。接下来我们进行简单的推导：
同样假设存在两个信号 ， ，其表达式如下：
其中 , 两个频率相近，利用三角函数和差化积可得：
其中 ， ；
通过分析我们可以发现：首先，拍频为两个信号时域上的叠加，故其频率成分未发生变化，依旧是两个频率相近的峰值，与幅值调制后的已调载波非常类似；其次，观察其和差化积后的结果我们可以发现，拍频现象实际上可以理解为一个频率为 的调制信号对频率为 的载波信号进行调制，但是并没有再次叠加载波信号，因为不论是调制信号还是载波信号都不是真实存在的。下面我们以一个实例进行更为直观的分析。
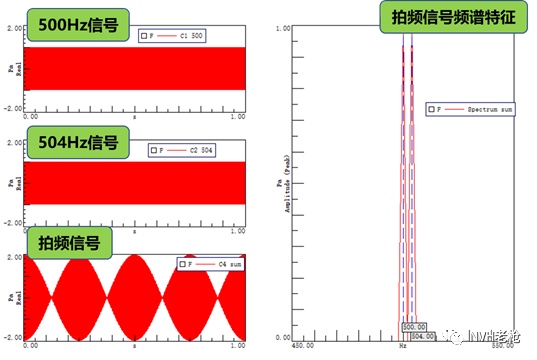
首先我们假设存在一个504Hz的正弦波，其表达式为 ；同时存在一个500Hz的正弦波，其表达式为 。将两个信号时域相加，从而得到拍频信号（如图5所示）：
图5 500Hz与504Hz信号所产生拍频信号的时域及频域分析结果
从图中我们可以发现，拍频信号整体幅值呈现每秒中4次的变化，即调制频率变为4Hz，为两个信号的频率之差。同时拍频信号的频谱特征中只包含了两个合成信号的频率信息并未发生任何改变，依旧为500Hz与504Hz两个频率峰值。基于上述我们的讨论，实际上我们可以理解为一个2Hz的调制信号对一个502Hz的载波信号进行调制，但是并未叠加原始载波信号故只产生了两个边频信息，而并没有代表载波信号频率信息的中心频率存在。
所以对于拍频现象来说，两个纯音的频率差即为其调制频率，揭示了合成信号整体幅值的周期性变化特征。调制频率是基于两个纯音的频率差而不是两个纯音自身频率。例如：100Hz纯音与120Hz纯音发生拍频时，其调制频率为20Hz。1000Hz纯音与1020Hz纯音发生拍频时，其调制频率也为20Hz。所以在分析拍频问题时，不要把调制频率与产生拍频问题的纯音自身频率混淆。
小结
基于上述的分析我们发现，NVH工程问题中的幅值调制与拍频现象从形成机理上存在着本质的区别，但是最终的表现形式又非常的类似。
首先，幅值调制噪声是两个频率相差较大的信号（通常表现为低频的调制信号与高频的载波信号）在时域内相乘并叠加原始载波信号，从而形成幅值调制噪声。其调制频率为低频调制信号的频率，最终的问题噪声的整体幅值在时域内呈现周期的变化。
然而，拍频现象是两个频率相差非常小的纯音在时域内叠加，形成的噪声现象。其问题噪声的调制频率为两个纯音频率之差，与两个纯音自身的频率信息无直接关系。同时拍频现象同样表现为整体幅值在时域上呈现周期性变化。
所以，不论是旋转机械的幅值调制噪声，还是声音的拍频，均可以通过同样的分析手段对其影响人类听觉的主观感受程度进行评判。分析过程中，牵涉到两个最重要的参数：调制频率 以及调制深度 （如图6所示，图中绿色曲线为调制信号的包络曲线）。关于调制信号关于这两个参数的分析评价，我们将在下篇中进一步阐述。
图6 声音的幅值调制可以通过调制频率与调制深度进行描述
- 下一篇：商用车自动驾驶测试现状研究
- 上一篇：汽车电线VOC检测乙醛超标分析
广告
最新资讯
-
基于场景体验的汽车智能座舱设计策略
2024-04-27 21:40
-
广汽研究院陈学文：以敬畏之心研发智驾，用
2024-04-27 21:37
-
LabVIEW+套件深度揭秘系列 | 如何用DIAdem
2024-04-27 21:30
-
哪些车企已经掌握了“坦克掉头”技术，如何
2024-04-27 21:27
-
浅谈汽车RNC主动降噪的量产实践（下)
2024-04-27 21:23
广告
广告
