广告
基于耗散性理论的汽车底盘集成非线性鲁棒约束优化控制——吉林大学 & 一汽 & 亚太
2021-09-30 08:49:00· 来源：焉知智能底盘
来源 | 《中国机械工程 》第32卷第8期目前,自动驾驶电动汽车已经成为国内外汽车产业 的主要发展目标之一,而主动前轮转向 (active front steering,AFS)子系统和直
来源 | 《中国机械工程 》第32卷 第8期
目前,自动驾驶电动汽车已经成为国内外汽车产业 的主要发展目标之一,而主动前轮转向 (active front steering,AFS)子系统和直接横摆力矩控制(direct yaw-moment control,DYC)子系统是保证自动驾驶电动汽车在自动紧急转向等 极限工况下安全、稳定行驶的关键部件,但二者在自动紧急转向等极限工况下呈现出强耦合特性, 简单组合的集成控制方式难以解决二者的强耦合特性对系统稳定性和控制性能的影响,因此深入研究二者在自动紧急转向等极限工况下的集成控制问题是一项具有实际意义的工作。
AFS子系统和DYC子系统的集成控制方法按照控制模型类型可划分为线性集成控制方法、非线性集成控制方法和智能集成控制方法。线性集成方法多采用线性二自由度汽车模型作为控制模型,并基于线性鲁棒 控制方法设计AFS和DYC的集成控制器。例如:将轮胎等效 侧偏刚度作为线性二自由度汽车模型的不确定参数,并采用最优保性能控制方法设计AFS和DYC的集成控制器。将线性二自由度汽 车模型转化成线性分式变换结构控制模型,并采用鲁棒H∞状态反馈控制方法实AFS和DYC的集成控制。
基于左互质分解线性二自由度汽车模型建立变结构内模鲁棒控制模型,并通过优化Youla参数化公式中的自由参数矩阵实现AFS和DYC 的鲁棒集成控制。以线性二自由度汽车模型的传递函数为基础,采用特征轨迹方法计算AFS和DYC的控制输入量,进而实现AFS和DYC的集成控制。在汽车自动紧急转向等极限工况下,线性二自由度汽车模型无法准确表征汽车实际的强耦合动力学特性,使得线性集成控制方法具有较大保守性。
非线性集成控制方法和智能集成控制方法对 汽车自动紧急转向等极限工况下呈现出的强耦合 特性具有更低的保守性。例如:采用滑模控制方法计算校正汽车横摆角速度偏差和限制汽 车质心侧偏角相轨迹运动区域所需的广义横摆力矩,并基于轮胎逆模型将广义横摆力矩转化为AFS和DYC的控制输入,实现AFS和DYC 的集成控制。采用非奇异快速终端滑模控制方法分别计算AFS的前轮转角控制量和DYC的横摆力矩控制量,并基于汽车质心侧偏角相轨迹稳定区域加权AFS的前轮转角控制量和DYC的横摆力矩控制量,实现AFS和DYC的协调控制。
将四轮车辆动力学模型作为控制模型,并采用非线性模型预测控制方法设计AFS和DYC的集成控制器,提高了汽车的操纵稳定性。基于七自由度汽车动力学模型将AFS和DYC的集成控制问题转化成非线性最优控制问题,并通过Riccati方程求解该非线性最优控制问题。将七自由度汽车动力学模型作为非线性模型预测控制方法的预测模型,设计AFS和DYC的集成控制器,最小化汽车横摆角速度和质心侧偏角跟踪误差,提高汽车的操纵稳定性。采用模糊逻辑控制方法分别计算AFS的前轮转向角控制量和DYC的横摆力矩控制量,并基于模糊积分理论计算AFS的前轮转向角控 制量和DYC的横摆力矩控制量的权重系数,实现AF和DYC的集成控制。
基于多模型切换控制理论设计一系列AFS和DYC集成控制器,并采用模糊逻辑控制方法实现所设计的AFS和DYC集成控制器的平滑切换控制。虽然非线性集成控制方法和智能集成控制方法对汽车自动紧急转向等极限工况下呈现出的强耦合特性具有更低的保守性,但采用非线性集成控制方法和智能集成控制方法设计的汽车底盘集成控制器通常包含大量的待确定设计参数,需要借助专家经验来标定这些待确定设计参数,以实现预期的控制目标。本文基于耗散性理论设计了一种标定参数较少的非线性鲁棒控制器,以实现AFS和DYC的集成控制。
数学模型
简洁、高效的汽车动力学模型是汽车底盘集成控制系统设计的基础。忽略空气阻力和车身的纵向、垂向、俯仰和侧倾运动自由度,建立包含车身侧向和横摆运动自由度的汽车底盘集成控制模型,如图１所示。
汽车底盘集成非线性L２增益控制
本节在Backstepping设计架构下,基于非线性鲁棒控制理论设计汽车底盘集成非线性L2增益控制律,抑制系统的加性不确定性对系统性能输出的影响。同时,借助投影修正法在汽车底盘集成非线性L2增益控制律中引入系统乘性不确定性自适应律,通过实时估计和补偿系统的乘性不确定性来抑制其对系统性能输出的影响,进一步降低系统的保守性。由AFS和DYC的集成控制目标,可得系统的性能输出为
校正横摆力矩约束优化分配
在式(37)描述的目标函数权重矩阵中引入平滑过渡因子,可以使AFS子系统主要工作在汽车质心侧偏角相平面稳定区域内。同时,汽车质心侧偏角相轨迹越靠近相平面稳定边界,AFS子系统的权重越大,使得AFS子系统和DYC子系统在提升汽车操纵稳定性方面由共同主导作用平滑过渡到仅DYC子系统起主导作用。综上将校正横摆力矩约束优化问题转化为如下的非线性规划问题:
仿真结果及分析
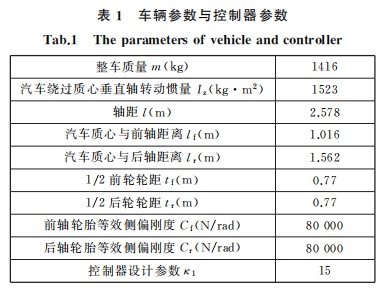
本节采用汽车动力学仿真软件CarSim构建模型在环测试系统,对所提出的汽车底盘集成非线性鲁棒控制器的可行性和有效性进行仿真验证。在仿真过程中,车辆参数与汽车底盘集成非线性鲁棒控制器参数配置如表1所示。
1、调幅正弦转向工况
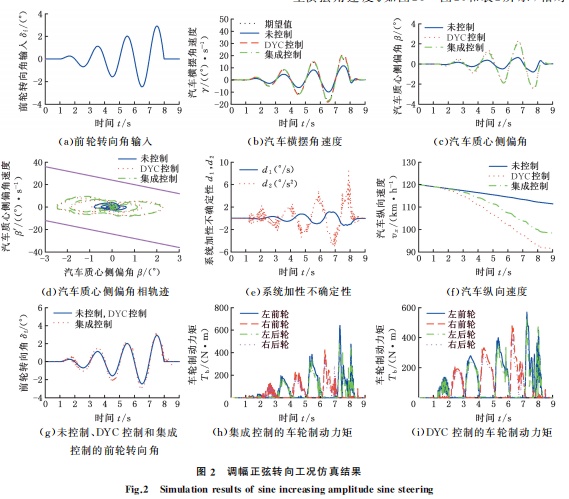
在调幅正弦转向工况中,汽车动力学仿真软件CarSim的路面附着系数设置为１,初始车速设置为120km/h,前轮转向角输入如图2a所示,正弦频率设置为3.14rad/s,调幅速率设置为0.477°/s,未施加控制,DYC控制和集成控制的仿真对比结果如图2b~图2i所示。
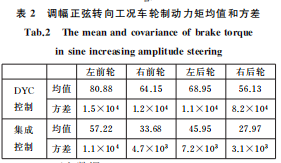
如图2b~图2e所示,在系统存在加性不确定性时,未施加控制,DYC控制和集成控制的汽车均保持稳定行驶状态,但是未施加控制的汽车无法跟随期望横摆角速度,呈现出不足转向趋势, 而DYC控制和集成控制的汽车可以准确跟踪期望横摆角速度。如图2f~图2i和表２所示,相对于DYC控制的汽车,集成控制的汽车需要的车轮制动力矩更小,对汽车纵向速度的影响更小。因此,本文提出的集成控制器既可以提高汽车操纵性,又可以抑制其对汽车乘坐舒适性的影响。
２、正弦延迟转向工况
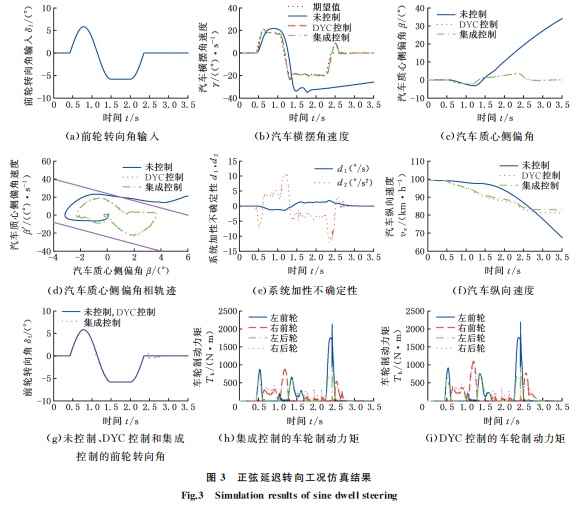
在正弦延迟转向工况中,汽车动力学仿真软件CarSim的路面附着系数设为0.8,初始车速 设置为100km/h,前轮转向角输入如图3a所示,幅值设置为5.82°,未施加控制,DYC控制和集成 控制的仿真对比结果如图3b~图3i所示。如图3b~图3e所示,在系统存在加性不确定性时,未施加控制的汽车在1.3s后失去稳定性,呈现出过多转向趋势,而DYC控制和集成控 制的汽车均保持稳定行驶状态,并且可以准确跟 踪期望横摆角速度。同时,相对于DYC控制的汽车,集成控制的汽车对期望横摆角速度的跟踪精度更高。
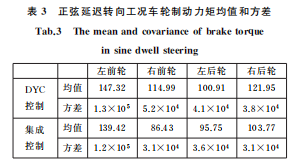
如图3f~图3i和表3所示,在正弦延迟转向工况中,汽车处于极限行驶状态,集成控制的AFS介入较少,但依然可以降低对车轮制动力矩的需求。因此,相对于DYC控制,本文提出的集成控制器既可以提高汽车操纵稳定性,又可以减小其对汽车乘坐舒适性的影响。
结论
(１)将汽车底盘集成控制模型建模误差考虑成系统的加性不确定性,并且将汽车整车质量、汽车纵向速度等信息测量误差考虑成系统的乘性不确定性,建立了包含车身侧向和横摆运动自由度的汽车底盘集成控制模型。
(２)基于耗散性理论和投影修正法设计了汽车主动前轮转向子系统和直接横摆力矩控制子系统集成非线性L２增益控制律,抑制系统加性不确定性和乘性不确定性对系统性能输出的影响,并采用逐步二次规划法来实现了所设计控制律输出的校正横摆力矩约束优化分配。
(３)结合车辆动力学仿真软件对所设计的汽车底盘集成非线性鲁棒控制器的可行性和有效性进行仿真验证。
结果表明:本文设计的汽车底盘集成非线性鲁棒控制器对系统加性不确定性和乘性不确定性具有强鲁棒性,既可以提高汽车操纵稳。定性,又可以减小其对汽车乘坐舒适性的影响。后续将搭建硬件在环试验平台,进一步验证所设计的汽车底盘集成非线性鲁棒控制器的可行性和有效性。
吉林大学汽车仿真与控制国家重点实验室—张家旭
中国第一汽车集团有限公司智能网联研发院—赵健
浙江亚太机电股份有限公司智能汽车控制系统研究院—杨雄
广告 
广告
编辑推荐
最新资讯
-
系统级封装（SiP）在新能源汽车领域的应用
2024-12-23 08:51
-
车载通信框架 --- 智能汽车车载通信架构浅
2024-12-23 08:40
-
全国首例！武汉车网智联公司完成智能网联测
2024-12-23 08:39
-
R54法规对商用车轮胎的要求（下）
2024-12-23 07:39
-
为攻克油冷技术难题，舍弗勒申请一项电机转
2024-12-23 07:38
广告
广告
