广告
声品质客观指标概述——声音的调制（下）
2021-10-04 15:20:29· 来源：NVH老枪
在声品质客观指标概述声音的调制（上）中，就幅值调制和拍频这两种现象的机理给大家做了简要介绍，本篇将就声音调制现象的定量分析手段和方法进行探讨。3#老枪调
在声品质客观指标概述——声音的调制（上）中，就幅值调制和拍频这两种现象的机理给大家做了简要介绍，本篇将就声音调制现象的定量分析手段和方法进行探讨。
——3#老枪
调制频率分析
1. 包络分析
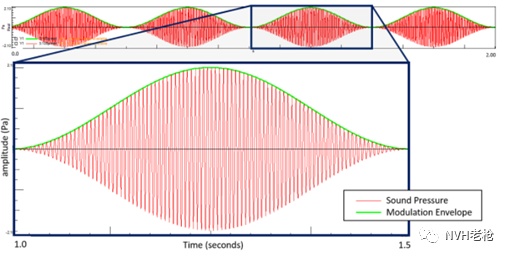
包络是描述快速变化信号总体轮廓特征的一种方法，包络函数的数学基础是由德国数学家大卫.希尔伯特（DavidHilbert）在20世纪初提出的，1998年黄锷（Norden E.Huang，中国台湾海洋学家）等人提出了经验模态分解方法，并引入了Hilbert谱的概念和Hilbert谱分析的方法，美国国家航空和宇航局（NASA）将这一方法命名为Hilbert-HuangTransform，简称HHT，即希尔伯特-黄变换。故目前针对声音的调制分析，首先需要基于希尔伯特-黄变换对信号进行包络分析。即获取图1中的绿色曲线。
图1 声音的幅值调制可以通过调制频率与调制深度进行描述
包络函数的一些特性包括：1. 基于绝对振幅，它永远不会低于零；2.比原始信号更能清晰反映低频信息。其中第二个属性可以帮助我们有效地分析听众对于声音的主观感受。如图2中的红色信号，一秒钟内有大约一百次的波动，而另一方面，听众可能更为关注绿色包络曲线所描述的振幅的缓慢变化情况，听众会听到每秒两次的波动，因为整体振幅每秒变化两次。这种差异会反映在原始信号的傅里叶变换与包络信号的傅里叶变换上。故为了获取准确的调制频率信息，需要进行调制谱分析。
图2 调制信号及包络曲线
2. 调制谱分析方法
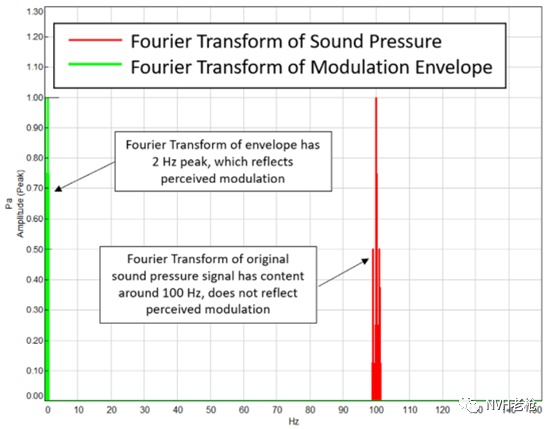
通过对包络信号进行傅里叶变换，可以得到声音调制的频率和幅度。如图3所示，在原始声压信号的傅里叶变换中没有显示出感知到的调制频率。其傅里叶变换结果（红色频谱）包含了100Hz的中心频率以及98Hz和102Hz两个边频；而包络线的傅里叶变换结果（绿色频谱）在2Hz处有一个峰值，该频率即为调制频率。表现了听众会听到整体振幅每秒变化两次。针对于信号包络线进行傅里叶变换的结果我们称之为调制谱。
图3 声压级信号及包络信号的傅里叶变换结果
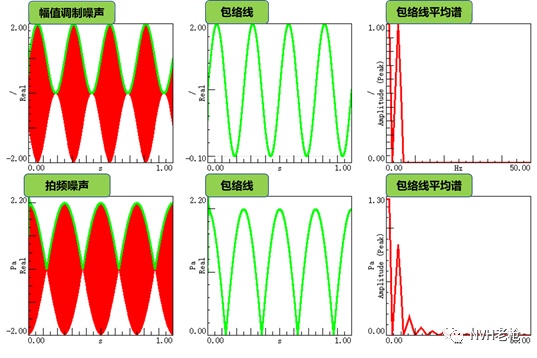
通过对幅值调制噪声与拍频噪声分别进行包络分析，我们同样可以发现两种问题的区别，从而帮助我们判别问题噪声的种类。
如图4的上图所示，对幅值调制噪声进行包络分析时其包络线为标准的正弦曲线，该包络线的傅里叶变换结果中只存在调制频率一个峰值（除去0Hz处峰值，因为0Hz处表现为该全正函数的平均值特征）。
而对拍频噪声进行包络分析时其包络线并非正弦曲线（如图4的下图所示），直观视觉感受就是曲线不够光滑、存在较为尖锐的“拐点”，该包络线所对应的傅里叶变换结果则表现为：除了调制频率所对应的最大峰值外，同时还存在若干谐频峰值。
图4 幅值调制噪声与拍频噪声包络分析结果的区别
调制深度分析
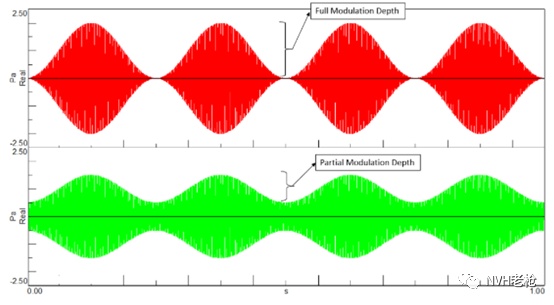
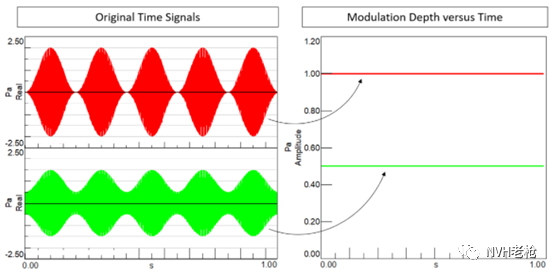
除了信号的调制频率，信号的调制深度的分析同样具有指导意义。如图5所示，这两个信号存在相同的调制频率，但是其“调制深度”不同，红色曲线比绿色曲线的调制深度更大，这种深度上的差异同样可以被听众感知到。
图5 两个信号具有相同的调制频率但调制深度不同
对于调制深度量级的定义有不同的定义形式：
绝对值：以dB为单位的绝对数值定义；
数字：用介于0~1之间的数字去定义调制深度，0表示没有调制，1则表示完全调制；（如图6所示）
百分比：0%表示没有调制，100%表示完全调制。
图6 调制深度的计算
调制分析在故障诊断中的应用
下面就让我们用一个工程案例，向大家展示如何应用相关分析手段，对调制问题进行故障诊断与优化。
1. 问题现象描述
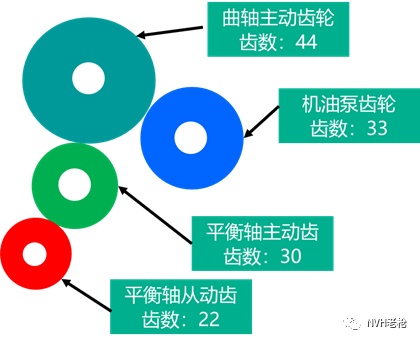
某发动机改款过程中添加了平衡轴，在样车诊断阶段发现了明显的齿轮啮合哨音。通过初步的信号特征分析发现，基于发动机转速的44阶啸叫明显，在常用发动机转速范围2000rpm附近异响无法接受。其传动示意图如图 7所示，希望通过相关分析判定该哨音是由哪对齿轮啮合产生。
图7 传动示意图
首先对问题声音信号进行滤波回放，该声音问题对于人耳听觉的主观感受表现为周期性的整体幅值变化，根据经验判定该哨音可能为声音的幅值调制问题，故进行声音调制的相关分析。
2. 幅值调制相关分析
首先选取问题工况即发动机定转速2000rpm工况下的发动机近场麦克风数据进行平均谱分析，其分析结果如图8所示。通过分析发现：
1. 1467Hz（2000rpm/60×44=1467Hz）处，即发动机转速44阶处，存在明显噪声，验证了问题描述的初步判定；
2. 在1467Hz处附近，存在较多边频。边频的出现，从侧面验证了之前我们认为该问题属于幅值调制问题的判断（与图3所展示的情况类似）。
图8 发动机近场噪声平均谱分析结果
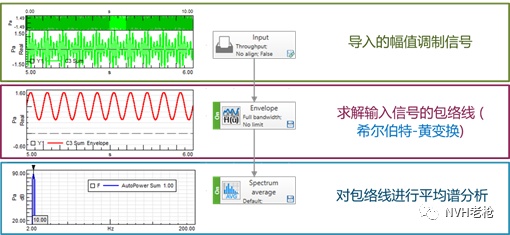
故对该近场噪声信号进行调制谱分析，即首先对其进行包络分析，求解包络线，再对包络线进行平均谱分析，求解包络线平均谱。具体操作步骤如图9所示。近场噪声包络线的平均谱分析结果如图10所示。（为避免其他频率噪声干扰分析结果，可首先对原始信号进行1300~1600Hz的带通滤波处理）
图9 包络线平均谱求解过程
图10 基于发动机近场麦克风数据的包络线平均谱求解
通过分析近场麦克风的包络线平均谱，我们可以发现，最大的两个频率峰值对应的频率分别为33Hz以及89Hz。由于发动机转速为2000rpm，其基频为33Hz。根据传动示意图可知：33Hz处峰值对应曲轴转动频率的1阶，89Hz对应机油泵主轴转速的2阶。具体阶次对应关系请参照表1所示。
表1 调制频率与结构件对应关系
由于不对中或者圆整度等问题，轴的转频及倍频会对啮合频率进行调制，所以调制频率所对应就是齿轮副某个齿轮所在轴的转频或是倍频。通过分析发现，主要的调制频率分别为33Hz（曲轴转频1阶），以及89Hz（机油泵主轴转频的2阶倍频）。故我们可以判定：该哨音主要来源是曲轴齿轮与机油泵齿轮啮合产生。只需要优化该对齿轮副即可完成问题优化。
3. 小结
本工程案例中，首先通过信号特征分析与滤波回放等手段，基于经验判定该噪声问题为典型的幅值调制问题，其次通过调制谱分析方法，准确地获取到调制频率，并根据传动机构的内部结构及速比，对照调制频率信息，最终判断出问题噪声来自于哪对齿轮副。
以上为笔者就声品质客观指标——声音调制分析进行的相关概述与讨论，希望对各位读者的工作能有所帮助。下一期文章还会继续该主题的讨论，为大家带来调制噪声分析领域中的另外两个声品质客观指标——波动度与粗糙度的介绍。
注：调制谱的计算方法其实是有两种不同的计算方式的，如图11所示。这两种方法的主要区别在于信号的平均值（直流成分），“Modulation Spectrum”方法会把信号的均值（0Hz处的数值）从频谱中进行了移除（图12左图中的绿色频谱）。故两种方法的计算结果只在0Hz处存在差异。对包络函数直接进行傅里叶变换后，之所以在0Hz处存在一个平均值，是因为包络函数是一个全正函数，因此有一个平均值（从零开始的偏移量），如图12左图中的紫色频谱所示。
图11 调制谱的两种不同计算方法
图12 调制谱不同计算方法的分析结果对比与原因分析
广告 
广告
广告
最新资讯
-
宁德时代CTC技术：引领电池与底盘一体化的
2024-12-24 21:33
-
海内外智能网联汽车数据空间研究与参考架构
2024-12-24 21:30
-
吉利全新一代域控式热管理集成模块下线
2024-12-24 21:28
-
智驾未来：技术架构与测评规范前沿| 第一期
2024-12-24 21:25
-
全固态电池试验线即将投产！
2024-12-24 21:24
广告
广告
