寻找供应商
广告
首页 > 振动与噪声 > 正文

汽车NVH 分析方法浅析

2021-10-06 11:39:12·  来源：汽车NVH云讲堂  
　
作者：孙 洋作者单位：（北京奔驰汽车有限公司，北京 100176）来源：汽车实用技术 摘 要：汽车在正式量产下线前会对车内噪音情况进行严格的管控，寻找到噪音源一
作者：孙 洋
作者单位：（北京奔驰汽车有限公司，北京 100176）
来源：汽车实用技术

摘 要：汽车在正式量产下线前会对车内噪音情况进行严格的管控，寻找到噪音源一直是NVH 审核时的难点。文章介绍了针对旋转器件产生的噪音现象进行的NVH分析，如何对分析软件的参数进行设置，以及主要参数在分析中所代表的意义，最后根据某车型噪音阶次分析结果寻找到噪音源。
关键词：NVH；阶次分析；旋转噪音
前言
NVH是noise vibration harshness 首字母的缩写，分别代表着噪音，振动和平顺性。其中最容易被客户抱怨的往往就是噪音。在对噪音信号进行分析时，最常用的是时域分析法。这种方法对于稳态信号具有较好的效果，能清晰地分析出被测信号的频率成分，从而确定故障原因。但是受到发动机的周期性激励，由于旋转部件故障引起的振动和噪音与发动机转速有密切的关系。难以利用某一时段信号的时域分析确定故障频率成分，有时候由于噪音信号频率的不断改变，会产生明显的“频率模糊”现象[1]，这样一来关键的频率成分就难以识别出来。这时等时间采样的分析方式在此就不再适用，我们需要不依赖于随转速变化的分析方法，阶次跟踪分析方法应运而生。
1 阶次跟踪分析原理
1.1 什么是阶次
在讨论阶次跟踪分析原理之前我们需要搞清楚什么是阶次。对于我们所关心的旋转部件噪音分析而言，阶次可以看作是旋转部件每旋转一圈所产生的事件次数。阶次为旋转部件的固定属性，以数字的形式进行表示。当零件在旋转时，会产生一定的响应事件发生，比如一个30 齿的齿轮，它旋转一圈，啮合这个响应事件就会发生30 次。如果我们把激励该齿轮旋转的齿轮定义为参考轴一阶次的话，那么这个30 齿的齿轮的阶次即30 阶次。所以阶次就是旋转部件产生的事件相对于转速的倍数。显然阶次是独立于转速的，对转速保持不变。这一特性对于我们确定噪音源零件非常有帮助。
1.2 阶次跟踪
阶次跟踪分析技术，其目的在于将等时间间隔采样的噪音信号转化为等角度采样的噪音信号，根据信号的频率变化对信号进行变速率采样，保证在每一个采样周期内都会有相同的采样点，这种跟踪激励源转速变化而相应改变采样频率的方法便称为阶次跟踪分析法[2]。假设齿轮旋转一圈采样10次，转速如果提升一倍，那么采样点就会变成5 次，这样一来齿轮旋转一圈产生的信号就没有完全捕获，这种漏采样会导致信号失真。为避免这种情况的出现，同步采样的需求应运而生，即等角度采样。还是刚才的例子，我们可以固定采样频率为齿轮每转36 度采样一次，这样即可实现齿轮旋转一圈永远可以采样10 次，不管激励频率如何改变，我们的采样的结果都不会失真。这种为了信号在各个采样周期里都会有相同数量采样机会的等角度采样分析法就是阶次跟踪分析。常针对旋转机械在某些工况下产生的噪音进行分析。
2.1 采集设备
采样频率fs 大于信号中最高频率fmax 的2 倍时，采样之后的数字信号完整地保留了原始信号中的信息，一般实际应用中保证 采样频率为信号最高频率的2.56~4 倍。鉴于人耳最大能听到的频率为20kHZ，所以我们在 录制噪音的时候一般会采用48kHZ 的采样频率。采样频率越高，产生的数据文件越大。1 分钟内4 通道均采用48kHZ 的话，将会产生33.8MB 的数据。对于通过结构传输的噪音，采样频率可以降低，一般为12kHZ，这是因为采样传感器固有的共振频率限制了测量范围，这个固有共振频率一般为5-6kHZ。

式中：fs为采样频率；fmax为最高频率
2.2 采集工况
在采集噪音时需要匀加速，尽量是的转速提升率为恒定值。对于旋转机械测试，最容易被测试者忽略的参数是转速变化速率。这个参数决定了频率分辨率和频率“拖尾”现象。对于随转速变化的信号来说，在一段数据的起始时刻与结束时刻转速变化如果十分明显，转速变化速率很大的话，起始时刻和结束时刻采样值的差异就会十分明显。如果这一段数据长度一定的情况下（频率分辨率决定了这一帧数据的长度），转速变化速率越大，频率拖尾越严重，阶次越不清晰。另一方面，转速变化速率对阶次切片也有影响，因此，转速变化速率的恒定对于数据分析相当重要。
3 噪音文件分析方法
3.1 常用分析方法
录到一个NVH 现象之后，下一步就是利用储存的数据分进行结果分析。常用的分析软件为Artemis 是通用分析软件，同样是来自海德声科公司，利用它可以进行多种声学和振动分析。对所发生的噪音和振动故障进行诊断。提升和优化产品质量。
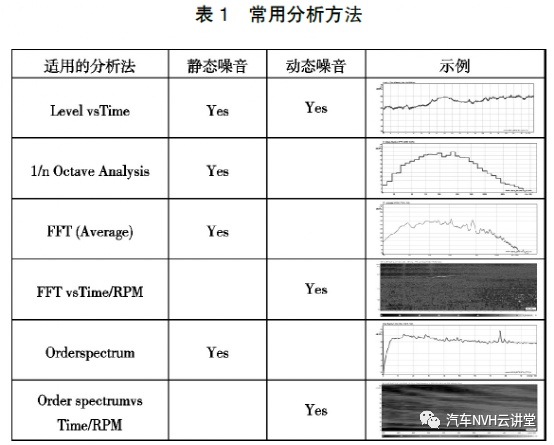
噪音基本上可以分为静态噪音和动态噪音。静态噪音指的是在恒定的驾驶条件下（恒定的速度与转速）所产生的噪音，比如路噪，风噪，刹车噪音。
动态噪音指的是跟速度和转速有关的噪音，比如差速器噪音，发动机变速箱噪音。
表1 所示为常用分析方法所适用的分析情况：

3.2 旋转部件的FFT分析法
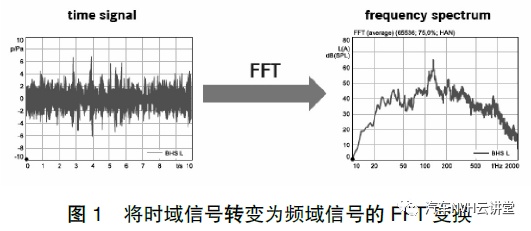
针对旋转部件产生的不确定噪音我们经常用到的分析方法为FFT。FFT（快速傅立叶变换）是离散傅立叶变换的快速算法。傅立叶表示为不同频率的正弦波信号的无限叠加。它帮助我们改变传统的时间域分析信号的方法转到从频率域分析问题的思维。有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了[3]。如图1所示。

3.3 FFT分析参数设置
3.3.1 频率分辨率
我们实际录制的噪音文件往往时间比较长，而FFT变换又只能分析有限长度的时域信号，因此需要将采样的噪音信号离散为一段一段的数据块。数据块的数量即Artemis 分析软件中的Spectrum size.如图2所示。不同的数据块数量会导致分析结果分辨率的不同，数量越多代表着对噪音信号源文件的分拆更加彻底，所以可以更加逼真的还原噪音信号。图3 表式不同的Spectrum size 会使得噪音信号更加清晰可见。

3.3.2 信号截断
当我们对噪音源信号进行截断的时候，很难做到周期性截断。因为源信号长度很难保证是周期的整数倍，而我们截断的时候也很难保证截断之后的信号开始时刻和结束时刻幅值相等。
图4 所示为对某正弦波的周期截断，假设将该源信号分割为该正弦波周期整数倍的数据段，每个数据段的起始时刻和结束时刻的幅值又刚好相等，即取样时间长度等于源信号的一个周期。那么将这些截断后的信号再重构，由于每段信号之间连续，重构时可以无缝连接，所以源信号得以完美还原，如图4-5 所示。

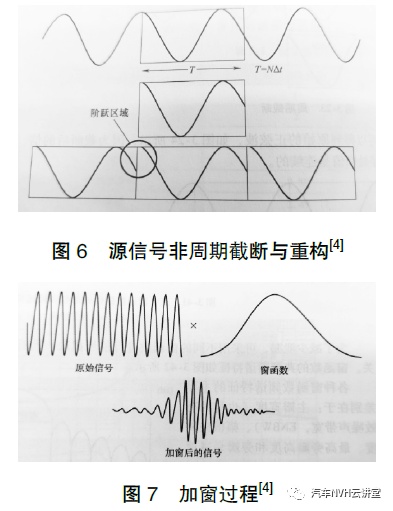
这种理想状态下的周期截断难以实现，实际操作中我们可以实现的往往是非周期截断。还是以刚才的正弦波为例，截断开始的幅值与结束时的幅值不相等，这就导致了在还原信号的时候出现不连续的阶跃区域，导致信号失真。图6 展示了源信号的非周期截断与重构。
为了降低信号泄露产生的误差，我们需要使用窗函数，将原始信号乘以一个窗函数，如图7 所示，相乘之后的信号具有了周期性，初始值和结束值相等，近似于周期截断，满足了傅里叶变换的需求。窗函数有很多种，常用的有汉宁窗，平顶窗，凯塞窗，布莱克曼窗。对于随机信号，拥有多个频率分量，并且分析时更侧重于频率点而非能量大小，则选用汉宁窗。

4 阶次分析结果
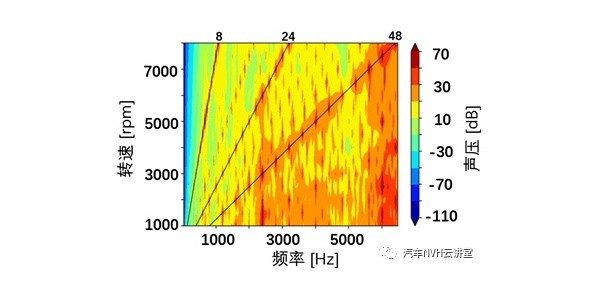
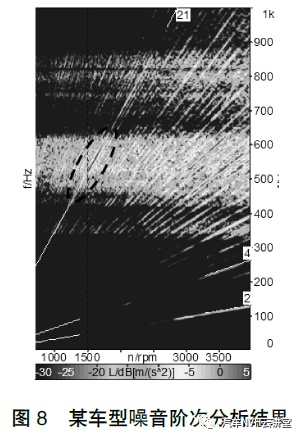
以图8 某车型噪音阶次图谱为例可以看出，在500-600Hz之间21阶噪音占据比较明显的成分，通过整车厂内部对于21 阶零件的定义，可以判断噪音来源可能是来自于凸轮轴。这时通过查阅凸轮轴相关的技术文件具体分析凸轮轴在该问题车上是否有比较明显的技术变更，以便确定问题的根本原因。

5 结论
在解决噪音问题往往是需要在有限的时间内提供有效的解决方案。阶次分析对于旋转零件的噪音源判定十分具有指导意义，通过其指定的分析方向可以让整车厂节约很多分析时间。在凭借自身对零件设计过程深厚的理解，往往可以很快找到问题的根源，大到排气管，优秀的汽车外形设计不仅是对汽车性能的优化，也是对潜在客户的感官吸引。虽然现阶段空气动力学在汽车外形设计方面的研究与应用取得了一些成就，但因为各种原因，空气动力学在汽车外形设计上的研究与应用还处在探索阶段，汽车气动特性理论远没有达到完善的地步。
 
分享到：
 
反对 0 举报 0 收藏 0 评论 0
  • 汽车测试网V课堂

    汽车测试网V课堂

  • 微信公众号

    微信公众号

  • 汽车测试网手机站

    汽车测试网手机站

• 车辆内部NVH测试解决方案 • 电动汽车电池包随机振动疲劳及优化分析
• 详解半主动悬置和主动悬置 • 某SUV车内加速轰鸣声问题分析与研究
• 车内噪声主动控制的参考信号选取方法 • 某车变速箱鬼频啸叫控制案例
• HBK电声产线测试解决方案 • 风洞内传声器阵列互谱矩阵的去噪
• 基于虚拟人工头的NVH优化 • SimNVH振动噪声分析软件功能介绍
0 条相关评论
  • 广告

编辑推荐

最新资讯

  • 广告
  • 广告
沪ICP备11026620号